Wektor estymatorów parametrów strukturalnych

Wartości teoretyczne zmiennej objaśnianej

Są to wartości zmiennej y wyliczone z modelu, a więc po zastąpieniu nieznanych, rzeczywistych wartości parametrów strukturalnych, ich ocenami, wyznaczonymi na podstawie próby według wzoru podanego powyżej.

Reszty modelu e

Są to różnice między wartościami empirycznymi a teoretycznymi zmiennej y. Stanowią podstawę tzw. weryfikacji statystycznej modelu:

Średni błąd modelu S_e

Błąd średni nazywany jest również odchyleniem standardowym reszt, lub pierwiastkiem z wariancji resztowej. Błąd ten jest liczony na podstawie reszt e_t (odchyleń wartości empirycznych y_t od wartości teoretycznych badanego zjawiska
) Obliczany jest według następującego wzoru:

gdzie n jest liczbą obserwacji, a k liczbą szacowanych parametrów.

Współczynnik determinacji R²

Mówi on o stopniu dopasowania modelu do danych empirycznych (a dokładnie o tym, jaką część całkowitej zmienności zmiennej objaśnianej stanowi zmienność wyjaśniona przez model). Jest miarą dobroci modelu (tzn. wskazuje na ile model jest dobry, a nie - jak w przypadku S_e - zły).

Współczynnik determinacji R² określony jest wzorem:

.

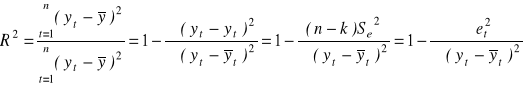
Wyrażony w procentach informuje, w ilu procentach model wyjaśnił kształtowanie się zmiennej objaśnianej.

Średnie błędy szacunku parametrów

Nazywane są również odchyleniem standardowym ocen parametrów. Błędy te mówią nam o ile średnio mylimy się szacując dany parametr α_j.

Aby wyliczyć błąd S(α_j) należy znać macierz (X^TX)^-1, której diagonalne elementy pomnożone przez wariancję resztową S_e² (kwadrat średniego błędu modelu) są wariancjami ocen poszczególnych parametrów. Jeśli zatem macierzą wariancji - kowariancji ocen parametrów jest D²(
)= S_e²(X^TX)^-1, a jej elementy diagonalne (leżące na głównej przekątnej) oznaczymy jako d_ij to błąd średni (odchylenie standardowe) oceny parametru zapiszemy jako:

Test t-Studenta

Służy do testowania istotności wpływu zmiennych objaśniających ma objaśnianą. Jest statystycznym narzędziem podejmowania decyzji co do istotności wpływu uwzględnionych w równaniu czynników na zmienną objaśnianą. Wnioskowanie o istotności zmiennych odbywa się pośrednio: poprzez wnioskowanie o istotności parametrów. W tym celu stawiamy następujący zespół hipotez:

H₀: α_j=0 (zmienna x_j jest nieistotna statystycznie)

H₁: α_j≠0 (zmienna x_j jest istotna statystycznie)

Ten zespół hipotez weryfikujemy za pomocą statystyki t postaci:

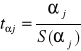
mającej rozkład t-Studenta.

Następnie należy wybrać właściwą wartość krytyczną rozkładu t-Studenta: t_kryt, którą odczytujemy dla:

• odpowiedniego poziomu istotności (jest to przeciwieństwo poziomu prawdopodobieństwa wnioskowania - poziomu ufności, najczęściej 0.05, czemu odpowiada 95% prawdopodobieństwo testu);

• odpowiedniej liczby stopni swobody równania, która jest różnicą pomiędzy liczbą obserwacji T a liczbą szacowanych parametrów k.

Decyzja o istotności lub jej braku jest następująca:

• jeżeli t_αj<t_kryt , to nie ma podstaw do odrzucenia hipotezy zerowej (parametr jest równy 0 i zmienna z nim związana jest nieistotna statystycznie);

• jeżeli t_αj>t_kryt , to odrzucamy hipotezę zerową na korzyść alternatywnej (parametr jest różny od 0 i zmienna z nim związana ma istotny wpływ na badane zjawisko)

Przedziały ufności dla parametrów:

Przedziały ufności wyznaczają granice w których znajdą się wartości parametrów z góry określonym prawdopodobieństwem. Wyznaczanie przedziałów ufności nazywane jest również estymacją przedziałową bo zamiast konkretnej, jednej wartości oceny parametru wyznacza się prawdopodobny przedział jego wartości, według wzoru:

α_j ∈ (
)

Przedziały ufności mówią nam, że z określonym prawdopodobieństwem przedział o podanych krańcach pokryje prawdziwą wartość danego parametru.

---