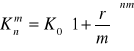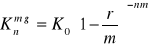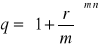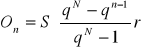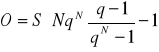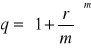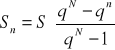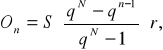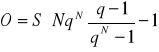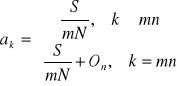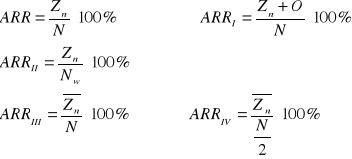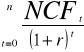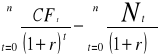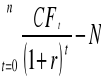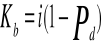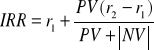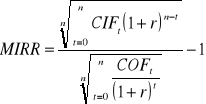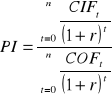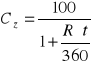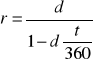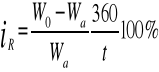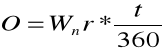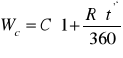PRZYSZŁA i OBECNA WARTOŚĆ KAPITAŁU
Stopa procentowa: ![]()
gdzie
( O - kwota odsetek, K0 - wartość kapitału początkowego, r- stopa procentowa).
Realna stopa procentowa to stopa uwzględniająca inflację ![]()
,
gdzie i-stopa inflacji.
Faktyczna stopa procentowa: ![]()
,
gdzie T jest stopą podatku od zysku z inwestycji kapitałowych.
Efektywna stopa procentowa: 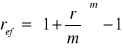
Przeciętna stopa procentowa 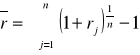
Kn -przyszła wartość kapitału K0 po n okresach czasu, r-nominalna stopa procentowa, m- liczba podokresów stopy procentowej (m-razy w ciągu roku, pełne okresy stopy procentowej)
|
Wartość bieżąca kapitału (dyskonto proste i składane):
![]()
,![]()
Dyskonto:![]()
Dyskonto matematyczne : ![]()
gdzie d - stopa dyskontowa (w%);
Dyskonto handlowe : ![]()
STRUMIENIE PŁATNOŚCI (WKŁADY OSZCZĘDNOŚCIOWE)
|
Liczba
nazywamy czynnikiem przyszłej wartości sumy wkładów oszczędnościowych.
ZWROT DŁUGÓW I KREDYTÓW. SPŁATY O ZADANYCH RATACH ŁĄCZNYCH
An - n-ta rata łączna, n-ta spłata, n-ta płatność,
Tn - n-ta rata długu, część długu spłacana w n-tej racie łącznej,
On - odsetki spłacane w n -tej racie,
Sn - reszta długu pozostała do spłacenia po spłaceniu n rat,
O - suma wszystkich odsetek.
|
We wzorach z punktu 1 wstawiamy zamiast r względną stopę procentową |
|
m - liczba spłat w okresie kapitalizacji, a - wysokość pojedynczej raty, m . N - liczba rat, A - umowna okresowa rata łączna, tzn. kwota płatności uiszczana w każdym okresie kapitalizacji
|
ZWROT DŁUGÓW I KREDYTÓW. SPŁATY O ZADANYCH RATACH DŁUGU
T1 + … + TN = S, T1=…= TN = T, T= Reszta długu pozostała do spłaty po n-ratach:
Odsetki:
Suma odsetek:
We wzorach z punktu 1) zamiast r wstawiamy
Ilość pełnych okresów kapitalizacji wynosi N, w ramach każdego okresu kapitalizacji następuje m spłat. Dług jest spłacany w m , N równych ratach. Okres stopy procentowej r jest równy okresowi kapitalizacji ( w przeciwnym przypadku należy zastosować względną stopę procentową).
m - liczba spłat w ramach każdego okresu kapitalizacji N - okres spłaty kredytu liczony w pełnych okresach kapitalizacji ak - wielkość pojedynczej raty
Wzory dla pełnych okresów stopy procentowej. W obrębie pełnych okresów kapitalizacja jest złożona, w odniesieniu do podokresów kapitalizacja jest prosta.
Odsetki On po n-pełnych okresach (n=1,...,mN):
Dług jest spłacany w N ratach, kapitalizujemy m-razy w ciągu każdego okresu, r -roczna stopa procentowa
|
STATYSTYCZNE METODY PROJEKTÓW INWESTYCYJNYCH
gdzie N -łączna suma nakładów[zł];CF - średnioroczne wpływy pieniężne[zł/rok]
P - całkowity przychód; c - cena sprzedaży/wyrobu; x-ilość sprzedanych jed.;
K=zx+S, K-koszty całkowite, z-jednostkowe koszty zmienne, S-koszty stałe;
Z0=P-K
Z0-zyska operacyjny;
Marginesy bezpieczeństwa inwestycji:
c-jednostkowa cena sprzedaży;
|
DYNAMICZNE METODY OCENY PROJEKTÓW INWESTYCYJNYCH 1.Wartość zaktualizowana netto
a) NPV=
b) Gdy nakłady ponoszone w kolejnych latach okresu obliczeniowego:NPV= gdzie CFt - to przepływ pieniężny związany z funkcjonowaniem przedsięwzięcia, N-globalne nakłady inwestycyjne w kolejnych latach okresu
c) gdy całość nakładów inwestycyjnych ponoszona jest w roku t=0
NPV=
2.Koszt użycia kapitału
IRR=NPV=0
PV-poziom NPV obliczonej na podstawie
NV- poziom NPV obliczonej na podstawie 5.Zmodyfikowana wewnętrzna stopa zwrotu
CIFt to dodatnie przepływy pieniężne w roku t, r- stopa dyskontowa stosowana przez inwestora (koszt kapitału) n- okres obliczeniowy(w latach)
6. Wskaźnik rentowności |
KRÓTKOTERMINOWE INWESTYCJE W PAPIERY WARTOŚCIOWE
WELSLE Wa=Wn-D, Wa-wartość rynkowa weksl, Wn-wartość nominalna (suma wekslowa), D-dyskonto;
d - stopa dyskontowa D=
rzeczywisty koszt złożenia weksla
BONY SKARBOWE
D=Wn - Cz gdzie
CERTYFIKATY BANKOWE
Wartość certyfikatu ze zmiennym kuponem: C= |
2
Wyszukiwarka
Podobne podstrony:
Wzory na zaliczenie z mechaniki plynow, studia, studia Politechnika Poznańska - BMiZ - Mechatronika,
MNK-interpretacja wzory, III semstr- studia
wyklad 8 - k.wlasny-RF, III semstr- studia
FiR-wyklad 10-podatek hodowy odroczony, III semstr- studia
Pytania na zaliczenie, Ochrona Środowiska studia, 3 rok (2008-2009), Semestr V (Rok 3), Monitoring i
pytania na zaliczenie-zagrożenia ekologiczne, Studia, Technologia Chemiczna, I stopień, PK, II semes
Wzory na zaliczenie z mechaniki plynow
Wzory na zaliczenie z mechaniki plynow
Wzory na zaliczenie
RF-wyklad 9-przychody i koszty, III semstr- studia
przyklad z rozwiazaniem, III semstr- studia
Pytania na egzamin III RM, Studia Ratownictwo Medyczne
rozklad RF!UL 2008 2009, III semstr- studia
Tematy na zaliczenie PP cw, Studia Zarządzanie PWR, Zarządzanie PWR I Stopień, I Semestr, Podstawy p
Inwestycja finansowa to inwestycja pośrednia, III semstr- studia
więcej podobnych podstron