Zagadnienia do egzaminu z matematyki

1. Algebra liniowa

1. Podaj definicję iloczynu skalarnego wektorów

2. Kiedy wektory są ortogonalne?

3. Podać definicję normy euklidesowej wektora x

4. Podać definicję kombinacji liniowej wektorów x₁, ..., x_m

5. Kiedy wektory x₁, ..., x_m ∈ Rⁿ nazywamy liniowo niezależnymi? Podaj przykład dwóch wektorów liniowo zależnych.

6. Podaj definicję macierzy.

7. Podaj przykład macierzy trójkątnej dolnej.

8. Jaki jest warunek konieczny mnożenia macierzy?

9. Które z poniższych wzorów są prawdziwe (A, B, C - macierze)

1. A+(B+C)=(A+B)+C

2. A+B=B+A

3. A(BC)=(AB)C

4. AB=BA

5. A(B+C)=AB+AC

6. (A+B)C=AC+BC

10. (A+B)^T=? (AB)^T=?

11. Wymień działania elementarne na macierzach.

12. Jak obliczyć wyznacznik macierzy stopnia n za pomocą rozwiniecia Laplace'a?

13. Co się stanie z wyznacznikiem macierzy A, jeżeli przestawimy w niej (zamienimy miejscami) dwa wiersze, a co - gdy przestawimy dwie kolumny?

14. Co się stanie z wyznacznikiem macierzy A, jeżeli jeden z jej wierszy pomnożymy przez 7, a co - gdy jedną z jej kolumn podzielimy przez 2

15. Podać definicję dopełnienia algebraicznego elemnentu a_ij macierzy kwadratowej A.

16. Podać definicję minora M_ij.

17. Podać definicję macierzy dołączonej do danej macierzy A.

18. Ile wynosi wyznacznik macierzy o dwóch liniowo zależnych wierszach?

19. Jakie są własności macierzy nieosobliwej?

20. Podać własności macierzy odwrotnej.

21. Czy wyznacznik ulega zmianie, gdy do elementów jednego wiersza dodać odpowiednie elementy innego wiersza pomnożone przez dowolną stałą?

24. Czy wyznacznik ulega zmianie, gdy do elementów jednej kolumny dodać odpowiednie elementy innej kolumny pomnożone przez dowolną stałą?

27. Jaki warunek musi spełniać macierz A, by istniała macierz odwrotna do niej? Podaj przykład macierzy, dla której nie istnieje macierz odwrotna.

28. Podać definicję rzędu macierzy.

29. Jakie operacje na wierszach macierzy (operacje elementarne) nie zmieniają rzędu macierzy?

30. Ile rozwiązań może mieć układ m równań liniowych o n niewiadomych?

31. Podać warunek konieczny i dostateczny rozwiązalności układu równań.

32. Kiedy układ n równań o n niewiadomych będzie

1. Oznaczony

2. Nieoznaczony

3. Sprzeczny

33. Kiedy układ równań liniowych jest układem Cramera?

2. Rachunek różniczkowy funkcji jednej i wielu zmiennych

1. Co rozumiemy przez granicę funkcji f(x) w punkcie x₀?

2. Podać definicję ciągłości funkcji w punkcie.

3. Kiedy mówimy, że funkcja f przekształca zbiór X na zbiór Y?

4. Kiedy funckja f jest różnowartościowa? Podaj przykład funkcji nieróżnowartościowej.

5. Podać definicję funkcji malejącej. Podaj przykład funkcji malejącej.

6. Podać definicję funkcji rosnącej. Podaj przykład funkcji rosnacej.

7. Podać definicję funkcji okresowej. Podaj przykład funkcji okresowej.

8. Podać definicję funkcji parzystej. Podaj przykład funkcji parzystej.

9. Podać definicję funkcji nieparzystej. Podaj przykład funkcji nieparzystej.

10. Naszkicuj wykres funkcji y=sinx oraz podaj jej własności.

11. Naszkicuj wykres funkcji y=cosx oraz podaj jej własności.

12. Podaj definicję funkcji odwrotnej. Podaj przykład funkcji wzajemnie odwrotnych.

13. Podaj przykład dowolnej funkcji cyklometrycznej (kołowej) oraz naszkicuj jej wykres.

15. Jakie warunki powinna spełniać funkcja f(x) aby posiadała funkcję odwrotną?

16. Podać definicję ilorazu różnicowego.

17. Podać geometryczną interpretację ilorazu różnicowego funkcji f(x) w punkcie x₀.

18. Co to jest pochodna funkcji f(x) w punkcie x₀?

19. Jak obliczyć pochodną sumy, różnicy, iloczynu i ilorazu funkcji f(x) oraz g(x)?

20. Podać geometryczną interpretację pochodnej funkcji f(x) w punkcie x_0.

21. Jak wyznaczyć przedziały monotoniczności funkcji stosując jej pierwsza pochodną?

22. Podajć definicję minimum (maksimum) lokalnego funkcji.

23. Sformułuj warunek konieczny istnienia ekstremum funkcji.

24. Sformułuj warunek wystarczający istnienia ekstremum funkcji związany ze znakiem pierwszej pochodnej.

25. Podaj definicję funkcji wklęsłej. Jaki znak przyjmuje wtedy druga pochodna funkcji?

26. Podaj definicję funkcji wypukłej. Jaki znak przyjmuje wtedy druga pochodna funkcji?

27. Kiedy funkcja f(x) może (ale nie musi) mieć punkt przegięcia w punkcie x₀ (warunek konieczny istnienia punktu przegięcia).

28. Podaj regułę de l'Hospitala.

29. Podaj definicję gradientu dla funkcji trzech zmiennych.

30. Podaj definicję hesjanu dla funkcji trzech zmiennych.

31. Jaka jest wartość gradientu funkcji wielu zmiennych w punkcie P, w którym istnieje ekstremum lokalne funkcji?

32. Podać twierdzenie o istnieniu ekstremum lokalnego funkcji dwóch zmiennych.

3. Rachunek calkowy funkcji jednej zmiennej

1. Kiedy mówimy, że funkcja F(x) jest funkcją pierwotną funkcji f(x)?

2. Podać definicję całki nieoznaczonej.

3. Podać postać formuły całkowania przez części.

4. Podać geometryczną interpretację całki oznaczonej.

5. Wyznaczyć całki sprowadzając je do funkcji elementarnych a następnie stosując wzory całkowe:

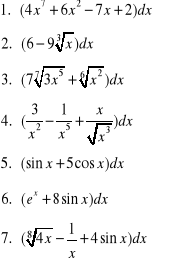
6. Obliczyć całki metodą podstawiania:

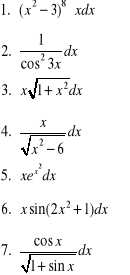
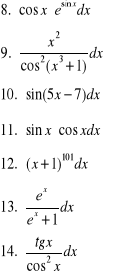
7. Obliczyć całki metodą całkowania przez części:

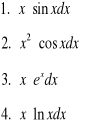
8. Obliczyć całki z funkcji wymiernych:

9. Oblicz pole powierzchni ograniczonej wykresami
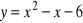
   i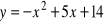
   

10. Oblicz pole powierzchni ograniczonej wykresami
    ,
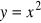
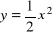
    i prostą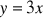
    

11. Oblicz pole ograniczone liniami: y² = x³, y=8, x=0.

---