Zjawisko fizyczne - fakt obserwacyjny (doświadczalny) będący przedmiotem badań w ramach fizyki. Prawo fizyczne - twierdzenie odnoszące się do zjawisk fizycznych, wystarczająco uzasadnione doświadczalnie (prawo fizyczne jakościowe). Prawo fizyczne ilościowe - zależność funkcyjna między wielkościami fizycznymi z uwzględnieniem w zapisie relacji przyczynowo - skutkowej. Teoria fizyczna - zwarty system praw opisujących zjawiska fizyczne lub klasę zjawisk fizycznych. Wielkość fizyczna - właściwość ciał lub zjawisk, które można wyznaczyć jakościowo i ilościowo, czyli można porównać z taką samą własnością innych ciał lub zjawisk (gęstość, natężenie prądu). Wielkości podstawowe - wielkości, które w danym układzie (np. SI) przyjęto jako niezależne od siebie i przy użyciu których wyraża się wzorami definicyjnymi wielkości pochodne.
Szybkośc- Uproszczony schemat metody fenomenologicznej (empirycznej) 1.Postawienie problemu (pytania), którego źródłem jest dostrzeżenie nowego faktu w czasie obserwacji otaczającej rzeczywistości, bądź w czasie przeprowadzonych eksperymentów, a także czasami przewidywanie teoretyczne. 2.Wykonanie szeregu doświadczeń w celu zbadania zależności między określonymi wielkościami fizycznymi. 3.Ustalenie zależności ilościowej wiążącej badane wielkości fizyczne - zapisanie wzoru, jako wniosku z eksperymentów. 4.Uogólnienie wniosków eksperymentalnych. 5.Sformułowanie prawa fenomenologicznego (empirycznego). Metoda idealizacji 1.Wyróżnienie czynników (wielkości fizycznych) istotnych w danym zjawisku. 2.Hierarchizacja w obrębie zestawu wielkości (W,W1, W2, ... ) 3.Wyróżnienie czynników (wielkości fizycznych) głównych i ubocznych. 4.Pominięcie czynników ubocznych, wprowadzenie założeń idealizacyjnych (tworzenie uproszczonego obrazu rzeczywistości - modelu rzeczywistości). 5.Ustalenie zależności funkcyjnej między wielkościami fizycznymi. Sformułowanie prawa idealizacyjnego. 6.Modyfikacja prawa idealizacyjnego przez znoszenie kolejnych założeń idealizujących (tzw. konkretyzacja prawa). 7.Aproksymacja jako ostateczny etap konkretyzacji prawa.
|
1. Układ odniesienia - ciało lub układ ciał, względem których opisywane jest położenie badanego ciała (z wybranym układem odniesienia wiąże się na ogół układ współrzędnych). 2. Ruch - zmiana położenia ciała względem innego ciała (układu odniesienia). 3.Punkt materialny - punkt obdarzony masą. Jest modelem obiektu fizycznego, którego rozmiary pomijamy. Ciało traktujemy jako punkt materialny wtedy, kiedy odległości przebywane przez to ciało są o wiele większe od jego rozmiarów, a jego struktura wewnętrzna nie ma znaczenia dla opisu jego zachowania. 4.Tor - linia zakreślana przez obrany punkt poruszającego się ciała w danym układzie odniesienia.
Wektor położenia - wektor, którego początek znajduje się w początku
Droga s - wielkość skalarna (długość toru)
Przyśpieszeni chwilowe: Ruch jednostajnie przyśpieszony
Ruch jednostajnie opóźniony
Ruch jednostajny, prostoliniowy v=const
Ruch niejednostajny, prostoliniowy
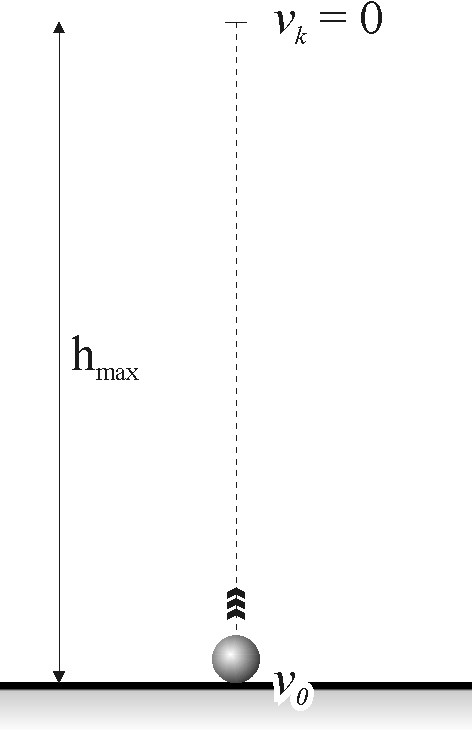
Rzut pionowy do góry
Rzut ukośny
Składowe prędkości początkowej:
Czas trwania ruchu:
|
v - prędkość liniowa
T - okres
Przyśpieszenie styczne i normalne
Przyspieszenie katowe
przyśpieszenie styczne
normalne
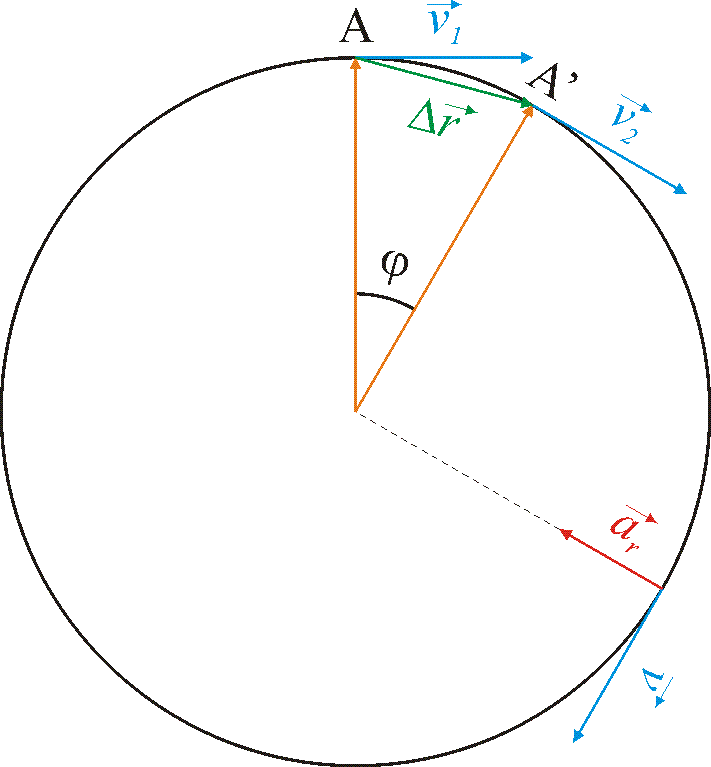
Przyśpieszenie dośrodkowe w ruchu po okręgu
|
Dynamika dinamix - dynamis (działanie) Podstawowym pojęciem w dynamice jest działanie (oddziaływanie) oraz jego ilościowa miara - siła. Philosophie naturalis principia mathematica (1686 r.) 1. Ciało pozostaje w spoczynku lub ruchu jednostajnym po linii prostej, jeśli działające na nie siły nie zmuszą go do zmiany tego stanu. 2. Zmiana pędu w czasie jest proporcjonalna do siły powodującej ruch i zachodzi w kierunku linii prostej, którą wyznacza kierunek działania siły. 3. Działaniu towarzyszy zawsze przeciwdziałanie, równe co do wielkości, lecz wprost przeciwnie skierowane (działania dwu ciał na siebie są zawsze równe i wprost przeciwnie skierowane). I zasada dynamiki spełniona jest tylko w inercjalnych układach odniesienia
wprowadźmy pojęcie pędu:
wynika z tego I zasada dynamiki
taką samą zmianę pędu można uzyskać z dużą siła w krótkim czasie, lub z małą siłą w długim czasie.
dla ruchu po okręguto zgodnie z II zasadą dynamiki działa siła:
III zasada dynamiki Jeżeli ciało A działa na ciało B siłą , to ciało B działa na ciało A siłą równą co do wartości bezwzględnej, lecz o przeciwnym zwrocie.
przyłożone są do różnych ciał !!!
|
gdzie: Fs - siła sprężystości, k- współczynnik sprężystości,
Dla niewielkich prędkości sił a oporu rośnie liniowo z prędkością. b- współczynnik oporu (zależy od kształtów ciała, rozmiarów, stanu powierzchni, właściwości ośrodka) Dla kuli:
Tarcie statyczne
Wyznaczanie fstat
Tarcie kinetyczne (poślizgowe
N - siła nacisku
Prawo powszechnego ciążenia (pr. Newtona)
Siła ciężkości Na ciało znajdujące się na Ziemi działa siła dośrodkowa, która jest wypadkową sił działających na ciało: F-siły grawitacyjnej R-siły reakcji podłoża Siła ciężkości to siła równa co do wartości sile , ale o przeciwnym zwrocie.
|
gdzie: M - ciało o masie M, źródło pola m - ciało próbne o masie m, nie deformuje pola wytworzonego przez źródło W otoczeniu każdego ciała przestrzeń posiada tę właściwość, że w każdym jej punkcie na ciało próbne działa siła grawitacyjna. Mówimy, że każde ciało wytwarza pole grawitacyjne.
- definicja wielkości fizycznej Pojęcie pracy
2. ၡ = 180o praca ujemna
3. ၡ = 90o W = 0
Praca siły grawitacyjnej
Tę wielkość fizyczną, która definiujemy jako stosunek pracy wykonanej przez siłę zewnętrzną przy przeniesieniu punktu materialnego o masie m = 1 kg z nieskończoności do danego punktu P pola, nazywamy potencjałem w danym punkcie pola (lub potencjałem danego punktu pola).
gdzie: M - masa źródła pola rP - odległość wybranego punktu P pola od źródła pola Związek między siłą grawitacji i potencjałem grawitacyjnym
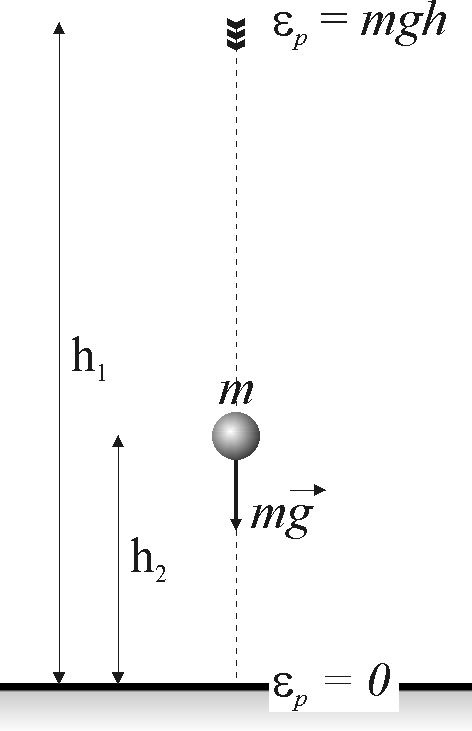
Praca siły ciężkości w polu jednorodnym
Potrafimy określić przyrost
Praca siły sprężystości
Praca W równa jest różnicy dwóch wyrażeń, które są funkcjami wychylenia ciała z położeni a równowagi.
Zasada zachowania energii
|
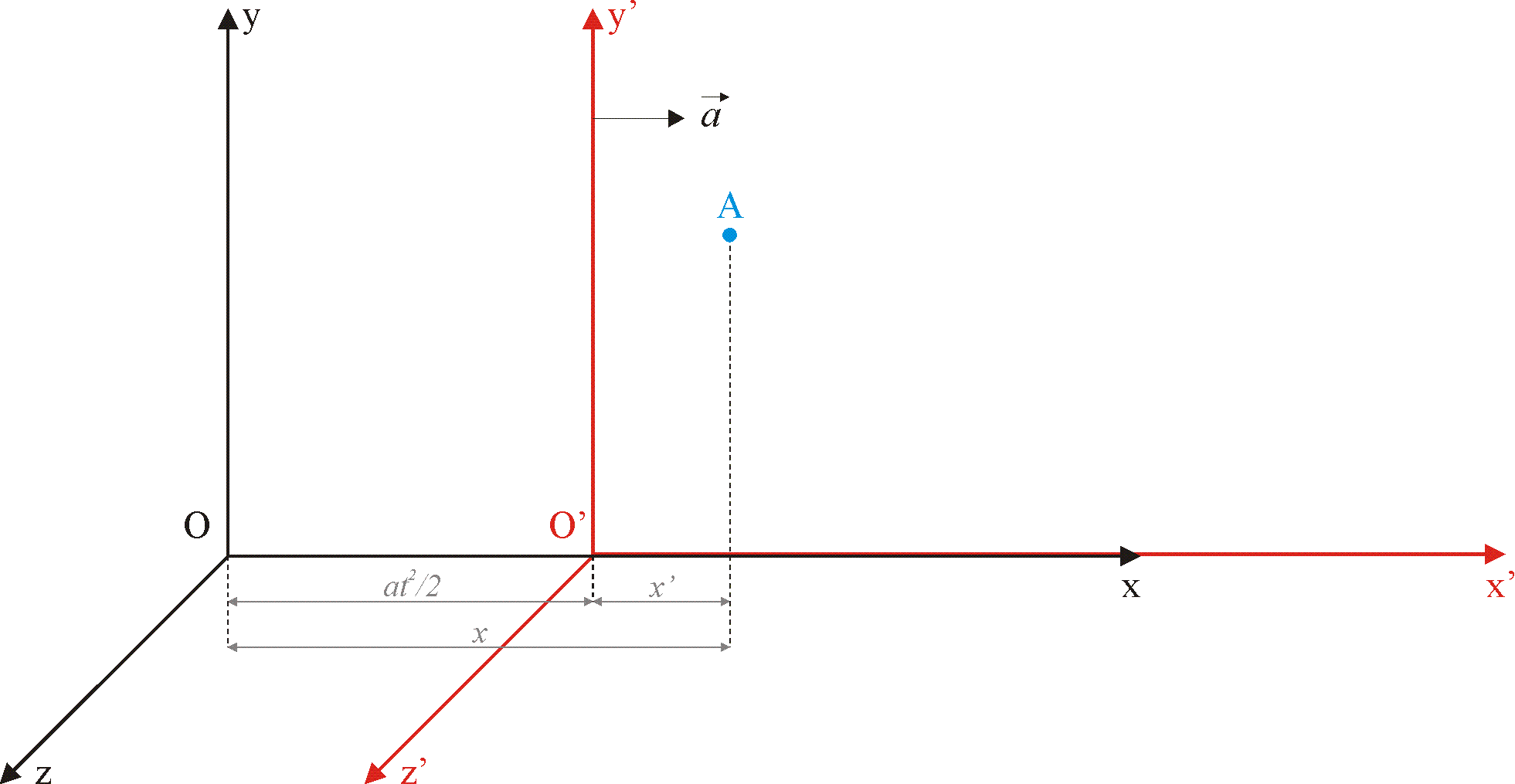
Siła bezwładności, nieinercjalne układy odniesienia
Układ odniesienia, w którym występują siły bezwładności nosi nazwę nieinercjalnego układu odniesienia. Układ poruszający się z przyśpieszeniem aႹ0 jest układem nieinercjalnym. Odśrodkowa siła bezwładności
Siła Coriolisa
|
Zderzenia Znane są początkowe pędy i energie kinetyczne cząstek przed zderzeniem. Należy znaleźć wartości (w przypadku pędu - kierunek) tych wielkości po zderzeniu W obszarze działają siły zderzeniowe (impulsowe). Natura tych sił może być różna; są to siły grawitacyjne, elektromagnetyczne, jądrowe. Siły zewnętrzne są tak małe, że można je pominąć i traktować zderzające się ciała jako układ odosobniony.
gdzie: k - zależy od właściwości materiału kul i jest proporcjonalne do ich promieni
Czas zderzenia np. protonu z jądrem atomowym wynosi około 10-22s, zaś czas zderzenia komety ze Słońcem - setki lat.
Dla kul stalowych o średnicy d = 203 mm oraz prędkości v = 0,6 m/s wynosi 0,000675 s.
Dwie kule stalowe o promieniach równych promieniowi kuli ziemskiej, poruszające się z prędkością v = 0,01 m/s mają czas zderzenia = 28 godzin. I. zasada zachowania energii
Jeśli E=0 , to zderzenia nazywamy doskonale sprężystymi
|
Bryła sztywna
nie zależy od czasu i nie zmienia się pod wpływem działających sił
Moment siły M-moment siły F przyłożonej w punkcie P względem punktu O
gdzie:
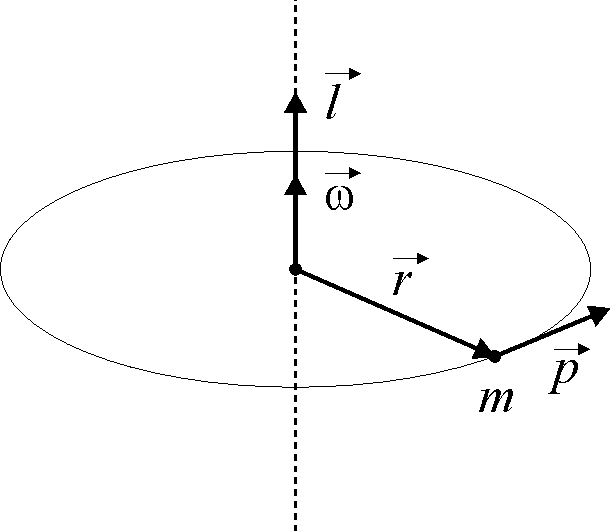
l - moment pędu punktu P
Moment pędu względem poruszającego się ze stałą prędkością, pozostaje stały podczas ruchu. Moment pędu punktu materialnego względem osi. Wyznaczamy moment pędu punktu materialnego P względem punktu O leżącego na osi.
Moment bezwładności
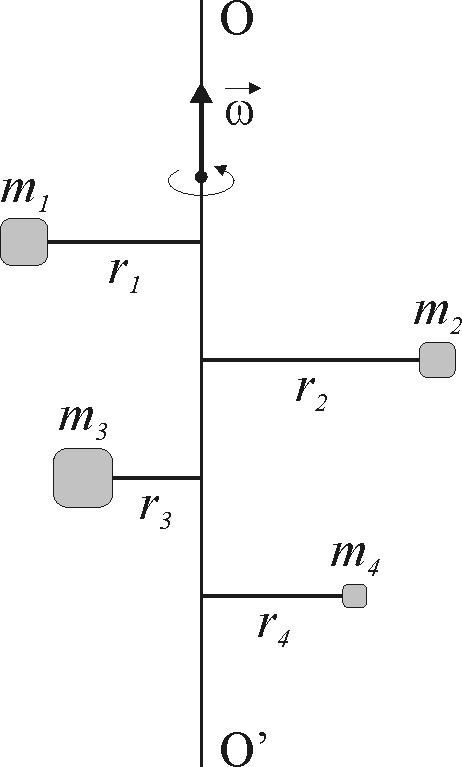
Twierdzenie Steinera oś przechodząca przez środek mas, równoległa do osi OO'.
względem tej osi
Moment bezwładności bryły względem osi OO' jest równy sumie momentu bezwładności względem osi równoległej do OO' i przechodzącej przez środek masy oraz iloczynu masy ciała przez kwadrat odległości obu osi. Prawa ruchu obrotowego bryły sztywnej
Szybkość zmiany momentu pędu równa się momentowi siły wypadkowej
ε - przyspieszenie kątowe
Zasada zachowania momentu pędu
Energia kinetyczna w ruchu obrotowym
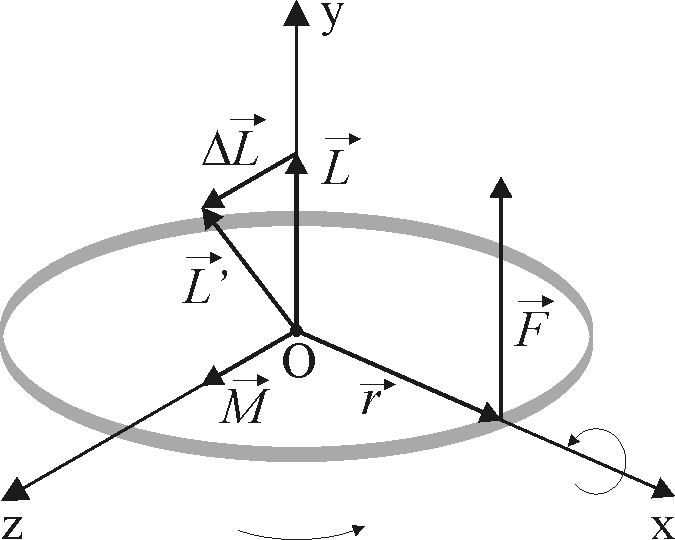
Bąk pod działaniem sił zewnętrznych
Wektor L a razem z nim oś symetrii obręczy, obróci się dookoła osi X! Zjawisko to nosi nazwę efektu giroskopowego Ruch postępowo-obrotowy bryły sztywnej
Toczenie np. walca można opisać jako złożenie ruchu postępowego i obrotowego lub jako „czysty” ruch obrotowy dookoła chwilowej osi.
|
równanie drgań tłumionych
rozwiązanie równania drgań tłumionych A0 - amplituda początkowa drgań
ၷ- pulsacja drgań tłumionych Dekrement tłumienia:
t tłumienia metoda wyznaczania współczynnika tłumienia ၤ
Czas relaksacji jes wprost proporcjonalny do masy ciała drgającego i odwrotnie proporcjonalny do współczynnika tłumienia. Drgania swobodne
rozwiązanie równania drgań
- pulsacja drgań swobodnych
Przemiany energii w ruchu drgającym
energia potencjalna w ruchu drgającym
Składanie drgań
Drgania wzajemnie prostopadłe
wzdłuż osi Y Superpozycja drgań harmonicznych wzdłuż jednej prostej Wprowadzamy pojęcie wektora amplitudy . Jest to wektor o długości A, wirujący z prędkością kątową ၷ, przeciwnie do ruchu wskazówek zegara. Rzut wektora amplitudy na oś OX zmienia się zgodnie z zależnością charakteryzującą drgania harmoniczne:
Obliczamy fazę ၪ drgania wypadkowego:
Drgania wymuszone. Zjawisko rezonansu.
Z II zasady dynamiki równanie drgań wymuszonych
|
Ruch falowy Równanie fali płaskiej
Umownie przyjmujemy, że zaburzenie ၹ = 0 odpowiada chwili przyjętej za początek rachuby czasu (t = 0). Niech zaburzenie (stan drgania) przesuwa się w przestrzeni np. w kierunku osi z. Wówczas cząstka znajdująca się w punkcie o współrzędnej z Ⴙ 0 będzie opóźniona w drganiach względem cząstki znajdującej się w punkcie 0 (z = 0) - źródła fali. Opóźnienie jest proporcjonalne do odległości „z” od źródła fali. Załóżmy, że stan drgań przesuwa się ruchem jednostajnym z prędkością V. Do punktu B', odległego od źródła fali (punktu 0) o z', zaburzenie dociera z opóźnieniem t = z' / v Długość fali równa się drodze, jaką zaburzenie przebywa w czasie jednego okresu drgania źródła.
liczba falowa równanie fali płaskiej, harmonicznej
ၹ - wychylenie z położenia równowagi cząstki znajdującej się w odległości „z” od źródła fali, po czasie t ω - pulsacja źródła fali A0 - amplituda drgań źródła fali Fale, których czoło stanowi w przestrzeni trójwymiarowej powierzchnia kuli, zaś w przestrzeni dwuwymiarowej okrąg koła nazywamy odpowiednio falami sferycznymi i kolistymi. Fale takie pochodzą od źródeł punktowych. Amplituda fali kulistej maleje wraz ze wzrostem odległości od źródła. Przy założeniu, iż nie ma strat energii, amplitudę fali opisuje wzór:
R - promień źródła fali r - odległość od źródła A0 - amplituda w odległości 1m od źródła
równanie fali kulistej Interferencja fal Źródła Z1 i Z2 są źródłami fal sinusoidalnych rozchodzących się w ośrodku izotropowym, jednorodnym. Niech fale te będą wzbudzane przez punktowe źródła Z1 i Z2, których pulsacja drgań równa się odpowiednio ၷ1 i ၷ2, a fazy początkowe wynoszą ၪ1 i ၪ2.
maksimum interferencyjne
minimum interferencyjne Fale stojące
Falę płaską biegnącą wzdłuż osi x opisuje równanie:
Zasada Huygensa-Fresnela. Ugięcie fal 1Źródło fali Z można zastąpić układem fikcyjnych źródeł fal wtórnych. Jako te fikcyjne źródła można przyjąć małe odcinki zamkniętej powierzchni otaczającej źródło Z. 2. Źródła wtórne są spójne. Za powierzchnię S przyjmuje się powierzchnię falową. Wtedy fazy drgań źródeł wtórnych są takie same, a także moce wtórnych źródeł są jednakowe. 3. Amplituda fali wtórnej jest tym mniejsza im większy jest kąt ၡ, jaki tworzy kierunek fali z normalną do powierzchni. Amplituda = 0, gdy 4. Jeżeli część powierzchni S jest zasłonięta, fale wtórne wysyłane są tylko przez odsłoniętą część powierzchni S. Wysyłanie fal odbywa się tak, jak w nieobecności osłony Odbicie fali. Prawo odbicia Kąt odbicia fali równa się kątowi padania.
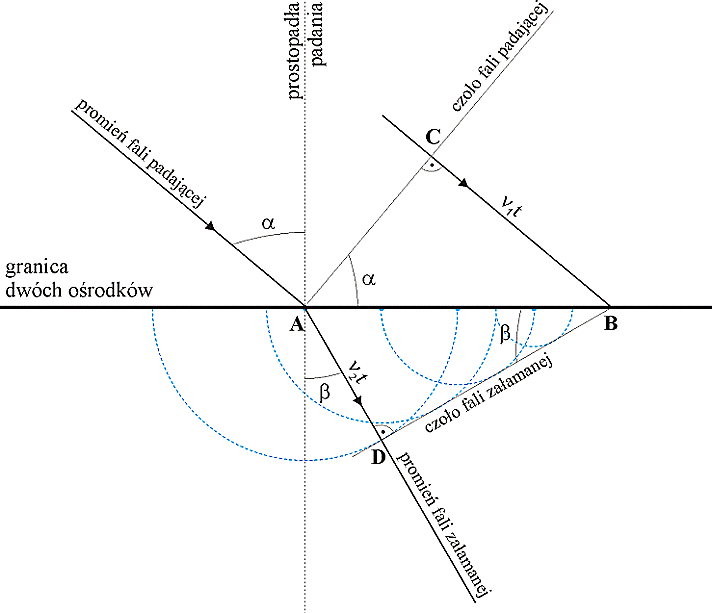
Załamanie fali. Prawo załamania
Natężenie fali Rozchodzenie się fali polega na przekazywaniu energii (w przypadku fal mechanicznych - przekazywaniu energii ruchu drgającego cząstek ośrodka). Natężeniem fali nazywamy wielkość liczbową równą ilości energii przenoszonej w jednostce czasu przez jednostkę powierzchni prostopadłą do kierunku rozchodzenia się fali.
|
Tłumienie fal Rozchodzeniu się fali w ośrodku towarzyszy pochłanianie energii (część energii drgań zamienia się w energię ruchu cieplnego). Załóżmy, że fala płaska przechodzi przez warstwę substancji o grubości x. Natężenie fali zmienia się od wartości I0 do I, przy czym I < I0. Przeźroczystość danej substancji D dla danej fali wyraża się stosunkiem:
Elementy akustyki Fale akustyczne są to fale podłużne rozchodzące się w ośrodku sprężystym. Źródłami fal akustycznych (głosowych) są ciała drgające (struny, membrany). Ucho ludzkie odbiera fale głosowe w przedziale częstości 20 - 20 000 Hz. Fale o częstości f < 20 Hz nazywamy infradźwiękami, a o częstości f > 20 000 Hz ultradźwiękami. W zależności od kształtu widma akustycznego rozróżniamy:
1. tony 2. dźwięki 3. szumy Dźwięki słyszalne charakteryzujemy podając: 1częstość drgań (wysokość dźwięku) 2. amplitudę drgań (głośność - natężenie dźwięku) 3. widmo akustyczne (barwę dźwięku) Głośność dźwięku o tej samej częstości i o innym natężeniu I określamy
prawem Webera Zjawisko Dopplera Gdy źródło jest nieruchome to w czasie t wysyła n zagęszczeń. W tym czasie pierwsze zagęszczenie przebędzie odległość s = Vdt
|
Równania Maxwella
prawo Gaussa dla pola elektrostatycznego
gnetycznego Strumień indukcji magnetycznej przez powierzchnię zamkniętą jest równy zero. Oznacza to, że linie pola magnetycznego są liniami zamkniętymi (nie istnieje monopol magnetyczny). Pole magnetyczne jest polem wirowym. Przez powierzchnię zamkniętą tyle samo linii pola magnetycznego wchodzi, co i wychodzi. Zmienne pola elektryczne i magnetyczne są ściśle są ściśle ze sobą związane tworząc jedno pole elektromagnetyczne. Pole te charakteryzują dwie wartości wektorowe W przypadku, gdy wzbudzone pole elektromagnetyczne zmienia się okresowo, rozchodzenie się tego pola w przestrzeni ma charakter falowy. Mówimy, że w przestrzeni rozchodzi się fala elektromagnetyczna.
Doświadczenie Younga Fale świetlne ulegają ugięciu na szczelinach (tak, jak fale na wodzie). Szczeliny S1 i S2 stają się punktowymi źródłami światła, rozchodzącego się z każdej szczeliny we wszystkich kierunkach
Polaryzacja światłaPrzyjmujemy za „reprezentanta” fali świetlnej wektor natężenia pola elektrycznego Model fali świetlnej spolaryzowanej w
kierunku osi Y Model fali świetlnej spolaryzowanej w
wzor Malusa |
Opis ruchu cieczy aPodajemy położenie każdej cząstki cieczy w funkcji czasu opis Lagrange'a b.Wybieramy punkt przestrzeni, rejestrujemy prędkości, z którymi przechodzą przez dany punkt cząstki cieczy - opis Eulera Rodzaje przepływu cieczy Przepływ ma charakter warstwowy. Cząstki cieczy nie przechodzą z warstwy do warstwy - przepływ laminarny Płyn miesza się (nie zachowuje charakteru warstwowego). Prędkość cząstek w danym punkcie zmienia się chaotycznie - przepływ turbulentny Kryterium podziału na ruch laminarny i turbulentny jest wielkość bezwymiarowa zwana liczbą Reynoldsa Re
ၮ - średnia (w przekroju poprzecznym) prędkość ၨ - współczynnik lepkości l - charakterystyczny rozmiar przekroju poprzecznego (dł. boku, średnica) Wprowadzamy pojęcie linii prądu: Linią prądu nazywamy krzywą w każdym punkcie styczną do prędkości cieczy przepływającej przez ten punkt. Linie prądu mają zwroty zgodne ze zwrotami odpowiednich wektorów prędkościUmówiono się, że gęstość linii prądu jest proporcjonalna do wartości prędkości w danym miejscu. W przepływie stacjonarnym każda cząstka, która przechodzi przez dany punkt przestrzeni, ma tę samą wartość prędkości, kierunek i zwrot. Linie prądu pokrywają się z torami cząstek cieczy. Obszar cieczy ograniczony liniami prądu nazywamy rurką prądu (strugą). Cząstki cieczy poruszają się wewnątrz rurki, nie przecinają jej bocznych ścianek. Równanie ciągłości Rozważmy strugę cieczy, wybierając dwa dowolne przekroje S1 i S2, przez które przepływa ciecz z prędkościami odpowiednio
Równanie Bernoulliego Stacjonarny strumień cieczy nielepkiej i nieściśliwej P1 - siła parcia na powierzchnię S1; P1 = p1S1 p1 - ciśnienie na powierzchnię S1 P2 - siła parcia na powierzchnię S1; P2 = p2S2 p2 - ciśnienie na powierzchnię S2
Przepływ cieczy przez okrągła rurę Rozkład prędkości płynu w różnych przekrojach cylindrycznych rury. Odległość miedzy przekrojami 1-1 i 5-5 nazywamy długością odcinka stabilizacji hydrodynamicznej. W przepływie cieczy istotną rolę odgrywa siła tarcia pomiędzy warstwami cieczy zwana siłą lepkości. W laminarnym przepływie cieczy siła lepkości między dwiema sąsiednimi warstwami, poruszającymi się z prędkościami ၮ, ၮ + dၮ wynosi: Fၨ - siła lepkości ၨ - współczynnik lepkości S - powierzchnia styku warstw
Wydajność strumienia cieczy Przy założeniu, że przepływ jest laminarny obliczamy tzw. wydajność strumienia cieczy Q. Wartość liczbowa Q równa jest objętości cieczy, która przepływa przez przekrój poprzeczny rury w jednostce czasu. Poprzeczny przekrój rury dzielimy na pierścienie o grubości dr. Przez pierścień o promieniu r przepływa w jednostce czasu ciecz o objętości równej iloczynowi powierzchni poprzecznego przekroju pierścienia 2ၰrdr i prędkości przepływu w odległości r od osi rury
|
Kinetyczno - molekularny model gazu doskonałego Założenia: -cząsteczki gazu są to punkty materialne, -poruszają się ruchem chaotycznym, -drogę między zderzeniami (fragment prostej) nazywamy drogą swobodną. Równanie gazu doskonałego, jako wniosek z teorii kinetyczno - molekularnej W sześciennym naczyniu o krawędzi l znajduje się N cząsteczek gazu m - masa cząsteczki ၮx - składowa prędkości cząsteczki w kierunku osi x
Energia wewnętrzna Przy założeniu, ze cząsteczki gazu są punktami materialnymi całkowita energia gazu jest energią ruchu postępowego cząsteczek. Nazywamy ją energią wewnętrzną U.
I zasada termodynamiki
Ciepło właściwe gazu (molowe) Doprowadzanie do 1 mola gazu ciepła o ilości dQ powoduje wzrost temperatury o dT (V = const).
Gazy rzeczywiste 1Między molekułami gazu rzeczywistego istnieją siły wzajemnego oddziaływania 2. Molekuły nie są punktami. Można je traktować jako doskonale sprężyste kulki
o promieniu rk i objętości
równanie Van der Waalsa P - ciśnienie V - objętość T - temperatura gazu |
|
I.ω = const.
dt
dL
Jeżeli M = 0, to ------ = 0, czyli L = const
a więc:
2
Wyszukiwarka
Podobne podstrony:
!!!! SPIS !!!!, 1) Geografia jako nauka - przedmiot badań geografii fizycznej
sciagaGN', OCENA-rezultat porównania rzeczy (zjawiska) z przyjętym kryterium zależnym od celu i prze
Obserwacja i doświadczenie jako najbardziej skuteczne i najczęściej stosowane metody nauczania, prow
Obserwacja i doświadczenie jako najbardziej skuteczne i najczęściej stosowane metody nauczania, prow
Badania jakościowe oraz obserwacja(1), Socjologia 2 rok, Metody badań społecznych
HLP - oświecenie - opracowania lektur, 19. Ignacy Krasicki, Mikołaja Doświadczyńskiego przypadki -PR
03 Obserwacja, Pedagogika społeczna, Metodologia badań społecznych, Badania jakościowe
Nawigacja-ćw.-Pozycja obserwowana, Szkoła, penek, Przedmioty, Nawigacja, Teoria
doswiadczenia podstawowe zjawiska fizyczne ich zastosowanie
F0-20!, Celem Cwiczenia jest poznanie fizycznych podstaw zjawiska termoelektrycznego i zapoznanie z
12, F-20, Celem Cwiczenia jest poznanie fizycznych podstaw zjawiska termoelektrycznego i zapoznanie
Badanie zjawiska piezoelektrycznego, Lab48v0, LABORATORIUM FIZYCZNE
12, F-20, Celem Cwiczenia jest poznanie fizycznych podstaw zjawiska termoelektrycznego i zapoznanie
Badanie zjawiska piezoelektrycznego, Lab48v0, LABORATORIUM FIZYCZNE
więcej podobnych podstron