BADANIE ZALEŻNOŚCI ZMIENNYCH:

Szereg wyliczający:

;
;
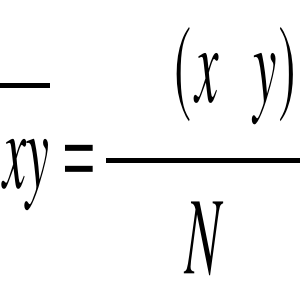
lub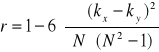

Macierz korelacyjna:

;

;

,

,

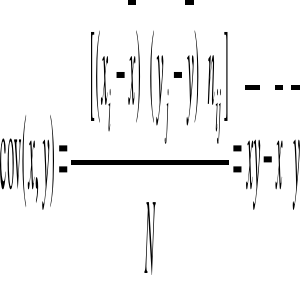
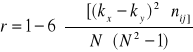
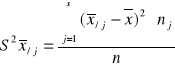
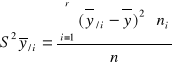
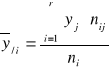
Oznaczenia:

• r_xy- współczynnik korelacji liniowej Pearsona,

• r- współczynnik korelacji liniowej Spearmana,

• e_xy, e_yx- stosunki korelacyjne zależności x od y i y od x,

• 
  ,
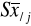
  - odchylenia średnich warunkowych zmiennych,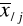

• 
  ,
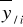
  - średnie warunkowe zmiennych,

• cov(x,y)- kowariancja zmiennych x i y,

• Sx, Sy- odchylenia standardowe zmiennej x, zmiennej y,

• 
  ,
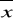
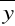
  - średnie wartości zmiennych,

• k_x, k_y- rangi zmiennych X oraz Y wyznaczane jako średnia arytmetyczna liczb porządkowych przypisanych danej wartości zmiennej uporządkowanej rosnąco,

• N- liczebność badanej próby,

• 
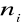
  - liczba wystąpień wartości x_i,

• 
  - liczba wystąpień wartości y_j,

• n_ij- liczba wystąpień pary x_i i y_j,

• r, (s) - ilość wartości zmiennej x (y); rxs- wymiary tablicy korelacyjnej

Pozostałe wzory bez zmian

LINIE REGRESJI

Pierwszego rodzaju:

Proste łączące punkty
;

;

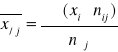
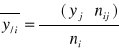
Drugiego rodzaju (równania regresji):

;
;
;

;
;

Badanie dopasowania równań regresji:

,

Oznaczenia:

• 
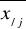
  - średnia wartość zmiennej x, pod warunkiem, że zmienna y przyjmuje wartość y_j,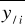

• 
  - średnia wartość zmiennej y, pod warunkiem, że zmienna x przyjmuje wartość x_i,

• y_i*- wartość zmiennej y wyznaczona z jej równania regresji dla zadanych x (teoretyczna),

• x_i*- wartość zmiennej x wyznaczona z jej równania regresji dla zadanych y (teoretyczna),

• a₁, a₀, b₁, b₀- parametry równań regresji,

• S_u² (S_v²)- wariancja resztowe równania regresji y względem x (x względem y)

Pozostałe oznaczenia bez zmian

UWAGI:

• wartość współczynnika korelacji zawsze zawiera się w przedziale <-1;1> i jej interpretacja jest następująca:

• r_xy<0- zależność zmiennych jest malejąca,

• r_xy=0- między zmiennymi nie zachodzi zależność liniowa

• r_xy>0- zależność między zmiennymi jest rosnąca

• |r_xy|<0,2- zmienne łączy bardzo słaba zależność liniowa

• 0,2≤|r_xy|<0,4- zmienne łączy słaba zależność liniowa

• 0,4≤|r_xy|≤0,6- siła zależności liniowej zmiennych jest średnia

• 0,6<r_xy|≤0,8- zależność liniowa zmiennych jest silna

• 0,8<r_xy|≤1- zależność liniowa zmiennych jest bardzo silna

• r_xy=±1- zależność x i y jest ściśle liniowa

• znaki kowariancji, współczynnika korelacji oraz parametrów: a₁ i b₁ muszą być takie same

• w przypadku badania zależności liniowej cech jakościowych korzysta się ze współczynnika korelacji liniowej Spearmana (r); współczynnik ten można również stosować do danych liczbowych o małej liczbie obserwacji (N<30) i przy częstej powtarzalności wartości

---