PRZEDZIAŁY UFNOŚCI

Szacowanie średniej w zbiorowości

a)
b)

Szacowanie odchylenia i wariancji w zbiorowości

(tylko gdy rozkład normalny)

a)
b)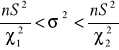
c)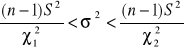

n>30 i m znane lub nieznane n≤30 i m znane n≤30 i m nieznane

Szacowanie wskaźnika struktury w zbiorowości

n≥100

Szacowanie współczynnika korelacji w zbiorowości

a)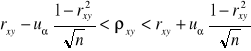
b)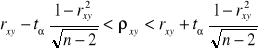

n>30 n≤30

Oznaczenia:

• n- liczebność próby

• u_α- wielkość odczytywana z tablic rozkładu normalnego dla: Φ
  

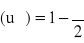
• t_α- wartość odczytywana z tablic dla zadanego α oraz liczby stopni swobody: k=n-1 (przedział ufności dla średniej) lub k=n-2 (przedział ufności dla współczynnika korelacji)

• 
  ,
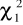
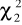
  - wartości odczytywane z tablic rozkładu χ² dla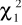
  -
  ,
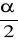
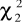
  -(1-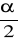
  ) oraz n- dla znanego m, albo (n-1)- gdy nieznana jest wartość m

• α- współczynnik istotności

• β- współczynnik ufności: α+β=1

• S- odchylenie standardowe odczytywane z próby

• 
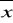
  - wartość średniej w próbie

• m- średnia w całej zbiorowości

• σ- odchylenie standardowe w całej badanej zbiorowości (dla n>30 przyjmuje się S=δ)

• w- wskaźnik struktury (miernik prawdopodobieństwa w badanej, dużej próbie)

• p- prawdopodobieństwo zajścia zdarzenia w zbiorowości

• r_xy- współczynnik korelacji w próbie

• 
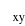
  - współczynnik korelacji w zbiorowości

Przy danej wartości
dokonuje się przeliczenia na S ze wzoru:

BŁĄD OSZACOWANIA PRZEDZIAŁU

Oznaczenia:

• G- górna wartość przedziału ufności

• d- dolna wartość przedziału ufności

• e- parametr wyznaczony z próby

• 
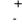
  - odchylenie od wartości z próby, określające błąd oszacowania

WYZNACZANIE LICZEBNOŚCI PRÓBY DLA ZADANEJ DOKŁADNOŚCI

PrzyjPrzyjęte oznaczenia jak powyżej.

WERYFIKACJA HIPOTEZ STATYSTYCZNYCH

Testowanie hipotez o średniej w zbiorowości

1) Hipotezy o jednej średniej

a)
b)

2) Hipotezy o dwóch średnich

a)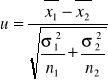
b)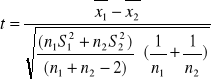

σ₁, σ₂ znane albo n₁ i n₂>30 n₁ lub n₂≤30 i δ₁, δ₂ nieznane, ale wiadomo, że δ₁=δ₂; rozkłady normalne

Testowanie hipotez o odchyleniu standardowym i wariancji w zbiorowości

(tylko gdy rozkład normalny)

3) Hipotezy o jednym odchyleniu (wariancji)

a)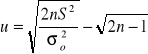
b)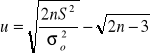
c)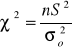
d)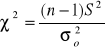

n>30 i m znane n>30 i m nieznane n≤30 i m znane n≤30 i m nieznane

4) Hipoteza o dwóch wariancjach

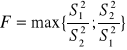
często przy badaniu hipotezy 2 w sytuacji b)

Testowanie hipotez o wskaźniku struktury w zbiorowości

5) Hipoteza o wskaźniku struktury.

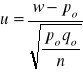
q_o=1-p_o n≥100

6) Hipoteza o dwóch wskaźnikach struktury.

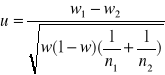
; n₁, n₂≥100

Testowanie hipotezy o istotności współczynnika korelacji

a)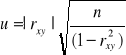
b)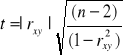

n>30 n≤30

Oznaczenia:

• m_o, σ_o, p_o (q_o)- założone hipotetycznie wielkości odpowiednio: średniej, odchylenia, wskaźnika struktury

• x₁- ilość obserwacji posiadających daną cechę w I-szej próbie

• x₂- ilość obserwacji posiadających daną cechę w II-giej próbie

• 
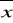
  ₁- wartość średniej w I-szej próbie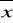

• 
  ₂- wartość średniej w II-giej próbie

• S₁- odchylenie standardowe w I-szej próbie

• S₂- odchylenie standardowe w II-giej próbie

• n₁- liczebność I-szej próby

• n₂- liczebność II-giej próby

• w₁- wskaźnik struktury w I-szej próbie

• w₂- wskaźnik struktury w II-giej próbie

• r_xy- współczynnik korelacji

• σ₁- odchylenie standardowe w I-szej zbiorowości

• σ₂- odchylenie standardowe w II-giej zbiorowości

Pozostałe oznaczenia bez zmian

STOSOWANE STATYSTYKI

1. Rozkład normalny: u_α- wielkość odczytywana z tablic rozkładu normalnego dla φ(u_α)=...:

1. 
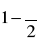
   - przy testowaniu hipotezy o równości np. m=mo

2. 1-α- przy testowaniu hipotezy o większości np. m>m_o

3. α- przy testowaniu hipotezy o mniejszości danego parametru w stosunku do zadanej wielkości np. m<m_o

1. Rozkład studenta- wartość t* odczytywana z tablic dla:

1. α oraz liczby stopni swobody k=(n-1), przy testowaniu hipotezy o równości średniej

2. 2α oraz k=(n-1) dla testów jednostronnych (dla testu o mniejszości bierze się -t*)

3. α i k=(n₁+n₂-2) przy testowaniu hipotezy o równości dwóch średnich

4. 2α i k=(n₁+n₂-2) przy testowaniu hipotezy o większości jednej średniej nad drugą

5. α oraz liczby stopni swobody k=(n-2), przy testowaniu hipotezy o istotności r_xy,

1. Rozkład χ^2*- wartości odczytuje się z tablic rozkładu dla:

1. 
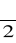
   oraz 1-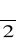
   i k=n stopni swobody, w teście dwustronnym przy znanym m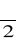

2. 
   oraz 1-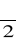
   i k=n-1 stopni swobody, w teście dwustronnym dla nieznanego m

3. α i k=n stopni swobody, przy testowaniu hipotezy o większości przy znanym m

4. α i k=(n-1) stopni swobody, gdy przy nieznanym m testowana jest hipoteza o większości

1. Rozkład Fishera-Snedecora. Wartość F* odczytywana jest z tablic rozkładu dla r₁=(n₁-1) i r₂=(n₂-1) stopni swobody, gdzie n₁ jest liczebnością tej próby, w której było większe odchylenie)

WARUNKI PRZYJĘCIA HIPOTEZ

1. H₀:- hipoteza o równości: |W|<T, lub w przypadku odrzucenia hipotezy o większości lub mniejszości badanego parametru od zadanej wielkości

2. H₁: Hipoteza alternatywna do H₀ przyjmowana w przypadku jej odrzucenia. Może dotyczyć:

• różności, gdy |W|>T

• większości, wtedy W>T

• mniejszości: W<T

Oznaczenia:

• W- wartości: u, t, χ², F- wyznaczone ze wzorów dla danych empirycznych

• T- wartości: u_α, t*,χ^2*, F*- odczytane z tablic

Test χ²

Stosowany gdy:

• dane pochodzą z dużej próby (n>30)wylosowanej w sposób niezależny

• dane są przedstawione w postaci szeregu rozdzielczego o r wariantach, liczebność dla każdego wariantu (n_i≥5)

• rozkład hipotetyczny jest ciągły lub skokowy

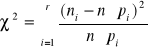
H₀: X ma założony rozkład; przyjmuje się gdy χ²< χ^2*

χ^2*- odczytywane z tablic dla α oraz r-s-1

Test Kołmogarowa

Stosowany gdy:

• dane pochodzą z dużej próby (n>30)wylosowanej w sposób niezależny

• dane są przedstawione w postaci szeregu rozdzielczego o r przedziałach, liczebność w każdym przedziale (n_i≥5)

• rozkład hipotetyczny jest typu ciągłego

;

H₀: X ma założony rozkład; przyjmuje się gdy λ< λ^*

λ ^*- odczytywane z tablic Kołmogarowa dla zadanego Q=1-α

Oznaczenia:

• n- liczebność próby

• r- liczba wariantów (przedziałów)

• s- liczba miar wyznaczonych z próby (s=0, jeśli nie trzeba było nic liczyć- wszystko było podane w założeniach; s= 1 jeśli liczono tylko średnią, jeśli liczono średnią i odchylenie s=2)

• n_i- liczebność w i-tym przedziale

• n_icum- liczebność skumulowana w i-tym przedziale

• p_i- prawdopodobieństwo teoretyczne obliczane ze wzorów lub odczytywane z tablic weryfikowanego rozkładu

• F(x)- dystrybuanta empiryczna wyznaczona ze wzoru:
  

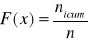
• F*(x)- dystrybuanta teoretyczna obliczana ze wzorów lub odczytana z tablic weryfikowanego rozkładu dla danego x_i

- 1 -

---