WZORY DO ROZWIĄZYWANIA ZADAŃ Z PRZEDZIAŁAMI UFNOŚCI

(zadanie 3 z pracy domowej i zadanie 2 z kolokwium1)

W przypadku, gdy określamy przedział ufności dla nieznanej wartości oczekiwanej m:

Model 1: X na rozkład N(m;σ), σ jest znane (podane w zadaniu), dowolne n:

Model 2: X na rozkład N(m;σ), σ jest nieznane, dowolne n:

Model 3: X ma dowolny rozkład, n ≥ 100

Model 4: X ma dowolny rozkład, n < 100 - brak wzoru

W przypadku, gdy określamy przedział ufności dla nieznanej wariancji σ²:

Model 5: X ma rozkład N(m;σ), n < 50

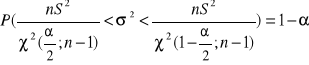
Model 6: X ma rozkład N(m;σ), n ≥ 50

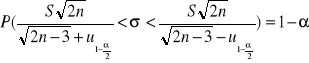
Oznaczenia:

1-  - poziom ufności (przedział ufności)

m - wartość oczekiwana

n - liczebność próby

- średnia z próby

S - średnie odchylenie standardowe z próby

σ - odchylenie standardowe

u_{1- /2} - kwantyl rzędu 1-/2 (z tablicy dystrybuanty rozkładu normalnego N(0;1) )

t(;n-1) - wartość krytyczna rozkładu t-Studenta o n stopniach swobody (z tablicy)

χ²(/2; n-1); χ²(1-/2; n-1) - wartości krytyczne rozkładu chi-kwadrat o n stopniach swobody (z tablicy)

Schemat postępowania w przypadku określania przedział ufności dla nieznanej wartości oczekiwanej m:

Patrzymy na rozkład prawdopodobieństwa:

jeżeli X na rozkład N(m;σ), a także:

• σ jest znane stosujemy model 1

• σ jest nieznane stosujemy model 2

jeżeli X ma dowolny rozkład:

• dla n ≥ 100 stosujemy model 3

• dla n < 100 model 4 (brak wzoru)

Schemat postępowania w przypadku określania przedział ufności dla nieznanej wariancji σ²:

Prawdopodobieństwo ma zawsze rozkład N(m;σ), w zależności od liczebności próby n:

• dla n < 50 stosujemy model 5

• dla n ≥ 50 stosujemy model 6

---