POLITECHNIKA WROCŁAWSKA

WYDZIAŁ GÓRNICZY

III GIF

Ćwiczenie projektowe nr 2

Temat: Dla zadanych warunków zaprojektować równostateczną skarpę metodą Masłowa a następnie sprawdzić stateczność metodą Felleniusa przy zadanym obciążeniu.

Wykonała:

Halina Mazurek

W praktyce budownictwa bardzo często konieczna jest ocena stateczności

zboczy (stoków) naturalnych, skarp wykopów (kanałów, wykopów fundamentowych) i skarp nasypów (zapór ziemnych, wałów przeciwpowodziowych). Nachylenie ich może być różne, zależne od rodzaju gruntu i jego właściwości fizycznych i mechanicznych, wysokości zbocza i działania wód podziemnych i powierzchniowych.

Sprawdzenie stateczności zbocza (skarpy) polega na obliczeniu minimalnego wskaźnika stateczności (bezpieczeństwa) F_min przy zastosowaniu odpowiedniej metody obliczeniowej, z uwzględnieniem geometrii układu warstw gruntu i przebiegu powierzchni poślizgu oraz odpowiednich parametrów gruntu. Wyznaczony wskaźnik F_min powinien być większy niż wskaźnik stateczności dopuszczalny F_dop dla danej metody obliczeniowej. W razie stwierdzenia niedostatecznego wskaźnika stateczności zabezpieczenie zbocza powinno polegać albo na zmniejszeniu sił zsuwających, albo na zwiększeniu sił utrzymujących zbocze.

Do obliczeń stateczności zboczy przyjmuje się pewne założenia upraszczające, które bezpośrednio wpływają na uzyskiwane wyniki. Często przyjmowanym uproszczeniem jest założenie powierzchni poślizgu o określonym kształcie i przebiegu, co ułatwia obliczenia.

Projektując skarpę równostateczną lub sprawdzając stateczność skarpy zakładamy:

• płaski stan odkształcenia,

• wytrzymałość gruntu opisuje hipoteza Coulomba tj.
  

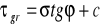
Miarą stateczności jest wskaźnik stateczności F, i gdy:

• F<1 - skarpa niestateczna

• F=1 - skarpa równostateczna

• F>1 - skarpa stateczna z zapasem bezpieczeństwa

Metody wymiarowania zboczy:

• empiryczne (Masłow)

• teoretyczne - oparte na teorii sprężystości i plastyczności (metody granicznego stanu naprężenia i metody równowagi granicznej).

Projekt skarpy równostatecznej metodą Masłowa (rys. 1)

Po wrysowaniu profilu skarpy należy połączyć punkt w podstawie z punktem w koronie - efektem końcowym jest wyznaczenie bezpiecznego kąta nachylenia skarpy przy danych rodzajach gruntu i wskaźnikach klasyfikacyjnych.

W gruntach niespoistych kąt nachylenia skarpy jest równy kątowi tarcia wewnętrznego gruntu

tg ၡ = tgၦ

W gruntach spoistych :

gdzie:

ၦ -kat tarcia wewnętrznego

c - kohezja (opór spójności) gruntu

ၧ - ciężar objętościowy gruntu

z - miąższość warstwy

Parametry geotechniczne warstw

Nazwa gruntu	γ [kN/m^3]	 []	c [kPa]
πp	20,601	21,5	38
Pś	16,677	33,5	-

Głębokość [m]	Rodzaj Gruntu	ၡ[Ⴐ]	[kPa]
2	πp	46,48	41,20
5	Pś	42,22	51,50
10	Pś	39,02	61,80

Pomierzony kąt wynosi: 26Ⴐ34'. Na jego podstawie wyznaczono dwa inne kąty, które wynoszą odpowiednio: 25Ⴐ i 35Ⴐ.

Sprawdzenie skarpy równostatecznej z dołożonym obciążeniem na naziomie

(metoda Felleniusa)

Przyjęto następujące założenia do tej metody:

• analiza w płaskim stanie odkształcenia,

• metoda równowagi granicznej,

• potencjalna pow. zniszczenia - cylindryczna przechodząca przez podstawę skarpy

• wszystkie siły sprowadza się do:

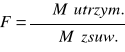
Sposób wykonania:

- rysunek skarpy w skali z dołożonym obciążeniem q,

• znaleziono linię środków obrotu - na podstawie kątów ၢ₁ i ၢ₂ zależnych od kąta nachylenia skarpy i od wysokości skarpy

• wrysowanie pierwszej potencjalnej linii zniszczenia

• podział potencjalnego klina zniszczenia na paski (Ⴃ 15)

• sprowadzenie działających obciążeń do podstawy paska

gdzie:

ၧ_i - ciężar objętościowy gruntu

A_i -powierzchnia paska

Q_n - obciążenie dodatkowe

• wyznaczenie sił utrzymujących i zsuwających i przedstawienie ich w postaci wektorów

-siły zsuwające

B = G_nთ sin ၡ_I

-siły normalne do linii zniszczenia

N = G_nთ cos ၡ_I

- siły utrzymujące

T = Nთ tgၦ + cთl

gdzie:

-ၡ_i - kąt pomiędzy styczną do linii zniszczenia a płaszczyzną poziomą

N - siły normalne

ၦ - kąt tarcia wewnętrznego gruntu

c - kohezja gruntu

• wyznaczenie wskaźnika stateczności skarpy F_i

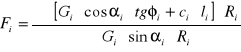
OBLICZENIA

Dla R₁ = 15,8 [m]

Numer paska	G [kN]	N [kN]	B [kN]	T [kN]	ၡ [Ⴐ]	T*R1 [kNm]	B*R1 [kNm]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

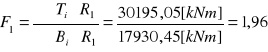
Dla R₂ = 16,7 [m]

Numer paska	G [kN]	N [kN]	B [kN]	T [kN]	ၡ [Ⴐ]	T*R2 [kNm]	B*R2 [kNm]
1	173,81	99,69	142,37	140,39	55	2344,54	2377,64
2	37,92	25,37	28,18	35,24	48	588,58	470,61
3	117,32	84,39	81,50	84,42	44	1409,83	1361,01
4	135,36	108,10	81,46	86,12	37	1438,27	1360,37
5	201,92	173,07	103,99	119,24	31	1991,23	1736,70
6	193,85	175,69	81,93	141,84	25	2368,79	1368,15
7	163,67	154,75	53,28	120,89	19	2018,91	889,84
8	199,74	195,38	41,53	157,03	12	2622,37	693,52
9	171,56	170,91	14,95	146,33	5	2443,67	249,71
10	132,42	132,34	4,62	138,13	2	2306,76	77,18
11	73,35	72,80	8,94	97,97	7	1636,18	149,28
12	40,26	39,23	9,06	96,34	13	1608,85	151,24
13	6,05	5,60	2,26	61,69	22	1030,25	37,82
					Σ	23808,23	10923,07

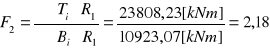
Dla R₃ = 18,1 [m]

Numer paska	G [kN]	N [kN]	B [kN]	T [kN]	ၡ [Ⴐ]	T*R3 [kNm]	B*R3 [kNm]
1	24,00	14,45	19,17	14,34	53	259,63	346,99
2	56,36	39,15	40,54	69,72	46	1261,93	733,74
3	105,51	80,82	67,82	98,26	40	1778,52	1227,52
4	135,75	112,55	75,91	96,57	34	1747,88	1374,02
5	118,97	105,04	55,85	85,13	28	1540,84	1010,90
6	135,96	126,93	48,72	107,24	21	1941,08	881,90
7	105,19	101,60	27,22	137,10	15	2481,44	492,75
8	97,08	96,14	13,51	130,43	8	2360,86	244,55
9	64,49	64,40	3,37	96,19	3	1741,00	61,09
10	20,73	20,68	1,45	86,90	4	1572,81	26,17
11	5,58	5,54	0,68	56,18	7	1016,81	12,31
					Σ	17702,80	6411,94

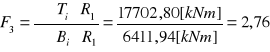
OBLICZENIE F_min

F₁ = 1,96

F₂ = 2,18

F₃ = 2,76

x₁= 0 [m]

x₂= 3,8 [m]

x₃= 7,6 [m]

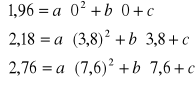
a = 0,012

b = 0,009

c = 1,96

wiec równanie będzie miało postać:

F = 0,012 x² + 0,009 x + 1,96

F^'(x)= 0,012 x + 0,009

x = -0,375

F_min (-0,375) = 1,95Wnioski

Analiza stateczności skarpy sprowadza się do ustalenia drogą kolejnych prób takiej powierzchni poślizgu, która dałaby najmniejszy współczynnik pewności F_min.

F_min Ⴃ F_dop

Wartości F_dop przy stosowaniu metody Felleniusa przyjmuje się w granicach od 1,1 do 1,3. Wiłun zaleca F_dop = 1,3.

W związku z powyższym warunek jest spełniony, wiec skarpa jest stateczna z zapasem stateczności.

---