SYMULACJA
1. Co to jest symulacja? Warto zaczac od próby podania definicji tego, czym jest symulacja.
Najprościej mówiąc, symulacja to technika służąca do imitowania działania całego systemu lub tez tylko naśladowania pewnej sytuacji (ekonomicznej, militarnej, mechanicznej, etc.) poprzez użycie odpowiednich modeli lub urządzeń w celu zdobycia informacji, czy tez w celach dydaktycznych.
Symulacja jest określana mianem sztuki i nauki jednocześnie. Jej celem jest stworzenie modelu całego systemu lub poszczególnego procesu, którym mozna by w ten sposób manipulować, aby w rezultacie dokonać oceny funkcjonowania badanego systemu, wystawionego na zmieniające się warunki. Jest to doskonale narzędzie analityczne, które w istotny sposób może ułatwić proces rozwiązywania problemów.
Oczywiście symulacja nie zawsze daje najlepsze z możliwych rozwiązań, ale jej rezultaty są o tyle cenne, ze są wynikiem wielu powtarzających się cykli. Poprzez zastosowanie metod statystycznych uzyskane wyniki staja się bardziej realistyczne, a zastosowanie grafiki komputerowej pozwala nawet laikom zgłębić mechanizmy działania badanego systemu.
Symulacja jest narzędziem, które pomaga zdeterminować, które z możliwych rozwiązań jest optymalne w obliczu postawionych wymagań. Ponadto trudno lekceważyć aspekt finansowy, na który w istotny sposób wpływa symulacja. Jej zastosowanie pozwala niemalże bezinwestycyjnie dokonać wyboru optymalnego rozwiązania bez wcześniejszego budowania fizycznie istniejącego systemu, co w wypadku projektowania i optymalizacji niezwykle kosztownych Elastycznych Systemów Produkcyjnych (Fexible Manufacturing Systems) jest bardzo duża zaleta.
2. Zastosowanie symulacji Użycie symulacji jako narzędzia do rozwiązywania problemów jest jedna z częściej stosowanych współcześnie technik, a obszary jej zastosowań to praktycznie wszystkie dziedziny nauki. Począwszy od systemów wytwarzania, procesów chemicznych i fizycznych, systemów dystrybucyjnych, transportowych, sieci komputerowych, aż do zastosowań w armii, wszędzie tam można pokusić się o dokonanie analizy przy użyciu metod symulacyjnych. Jedynie wyobraźnia użytkownika stanowić może barierę dla nowych zastosowań.
Należy jednak pamiętać, ze tak jak różne dziedziny nauki stosują różne metody poznawcze tak i w szerokiej gamie programów symulacyjnych dostępnych na rynku wyróżnić można grupy programów, których zastosowanie może czasami być ograniczone do rozwiązywania problemów tylko w określonym zakresie (np. SIMFACTORY jest programem stosowanym przede wszystkim do modelowania i symulacji fabryk).
3. Systemy, modele, i metody symulacji System definiowany jest jako zbiór obiektów (entities), np. ludzi, maszyn, które działają i oddziaływują na siebie w celu osiągnięcia jakiegoś logicznego wyniku [definicja proponowana przez Schmidt'a i Taylor'a (1970)].
W praktyce, to, co postrzegamy jako system, uzależnione jest od celów prowadzonych badań. Zbiór obiektów, które tworzą pewien system, może być jedynie podsystemem podczas badania jakiegoś innego systemu. Za przykład może służyć badanie działania banku, kiedy chcemy określić liczbę urzędników w okienkach, aby zapewnić odpowiednia obsługę klientów pragnących dokonać podstawowych operacji bankowych (wpłaty, wypłaty). W tym wypadku, system można zdefiniować jako cząstkę banku i ograniczyć go do dwóch obiektów: urzędników w okienkach i czekających w kolejce klientów. Jeśli jednak prowadzone badania maja obejmować dodatkowo urzędników z działu kredytowego lub marketingu wtedy należy przedefiniować system, dodając nowe obiekty i tworząc podsystemy.
W związku z powyższym należy pamiętać, ze definicja badanego systemu, zależy od założeń prowadzonych badań i opisuje system tylko uwzględniać pewien szczególny punkt widzenia problemu. W przypadku wspomnianego banku, dwa wyróżnione obiekty (urzędnicy w okienkach, klienci czekający w kolejce) można w zależności od innych założeń prowadzonych badań, uszczegółowić wprowadzając cztery obiekty: urzędników zajętych obsługą klientów, urzędników czekających na klienta, klientów obsługiwanych, klientów czekających w kolejce.
W trakcie trwania cyklu życia systemu zdarza się, ze jest konieczne przeprowadzenie analizy systemu, w celu zdobycia informacji o mechanizmach zachodzących w systemie, relacjach pomiędzy obiektami, aby przewidzieć zachowanie w zmienionych warunkach. Poniższy wykres przedstawia sposoby, w jaki można prowadzić badania systemu.
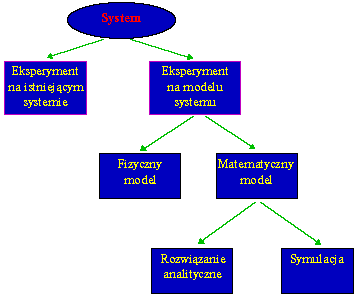
Rys. 1. Metody analizy systemu
3.1. System i model systemu Jest możliwe, i czasami ekonomicznie uzasadnione, poddawanie istniejącego fizycznie systemu nowym warunkom, a następnie dokonanie oceny jego funkcjonowania. Jest to jednak metoda, którą rzadko się stosuje, ze względu na koszty i zakłócenia normalnej pracy systemu.
Przykładowo wprowadzenie Elastycznego Systemu Produkcji bez uprzedniej analizy jego wpływu na pozostałe elementy systemu może okazać się nieuzasadnione (błędne) z ekonomicznego, technologicznego, czy technicznego punktu widzenia.
W takim przypadku konieczne jest zazwyczaj zbudowanie modelu projektowanego, czy tez już istniejącego systemu, aby następnie na jego podstawie analizować działanie rzeczywistego systemu.
Powstaje często jednak pytanie, do jakiego stopnia model odzwierciedla istniejący (projektowany) system. Znane są przypadki, ze pomimo uwzględnieniu ogromnej liczby szczegółów badanego systemu, jego model może tylko w niewielkim stopniu udzielić odpowiedzi na pytanie, jak system zachowa się w rzeczywistości.
3.2. Model fizyczny i model matematyczny Zdarza się, iż zbudowanie w odpowiedniej skali modelu fizycznego badanego systemu może być korzystne, a czasami wręcz niezbędne. W literaturze znaleźć można przykłady takich modeli. Mogą nimi być modele Elastycznych Systemów Produkcyjnych, czy tez makiety budynków wykonywane przez architektów. W ekstremalnych przypadkach zdarzają się także modele w skali 1:1, jak na przykład model baru szybkiej obsługi wykonany na zlecenie jednej z amerykańskich sieci barów.
Jednak w większości przypadków podczas analizy systemów powstają modele matematyczne, które reprezentują system za pomocą logicznych i kwantyfikatorowych relacji. Relacjami tymi manipuluje się w ten sposób, aby określić jak model reaguje na zmiany, a wiec jak zachowałby się istniejący system, pod warunkiem, ze model matematyczny jest odpowiednio zaprojektowany. Być może najprostszym przykładem jest znany wszystkim wzór na drogę S=v t gdzie v to prędkość, t czas, a S to odległość. Jest to jeden z najprostszych matematycznych modeli, oczywiście dokładność, w jaki model ten opisuje np. drogę fotonu do innej galaktyki, jest satysfakcjonująca, ale bardziej skomplikowane problemy byłoby już trudno opisać przy pomocy tej formuły.
3.3. Rozwiązanie analityczne i symulacja Zbudowany model matematyczny musi zostać przeanalizowany w celu sprawdzenia, czy może być zastosowany do opisu badanego systemu. Jeśli model jest wystarczająco prosty, istnieje możliwość zbadania działania systemu przy pomocy metod matematycznych i otrzymania w ten sposób rozwiązania analitycznego. Niektóre metody analityczne mogą być jednak niezwykle rozbudowane, co pociągałoby za sobą olbrzymia liczbę obliczeń. Znane są także przykłady, kiedy matematyczna formuła znana jest doskonale, ale jego rozwiązania dalekie jest od prostoty.
W przypadku, kiedy model matematyczny jest znany, a związane z nim obliczenia nie są zbyt skomplikowane, zazwyczaj zaleca się, aby zamiast symulacji wybrać drogę analityczna. Jednakże, wiele systemów ma tak wysoki stopień złożoności, ze ich matematyczne modele wykluczają możliwość analitycznego rozważania. Wtedy badany model musi być analizowany przy użyciu metod symulacyjnych..
4. Klasyfikacja modeli symulacyjnych Kiedy zdecydujemy, ze model matematyczny badanego systemu poddamy eksperymentowi symulacyjnemu, wtedy należy dokonać wyboru narzędzia odpowiedniego do specyfiki analizowanego problemu. W takich przypadkach celowa jest klasyfikacja modeli symulacyjnych wzdłuż trzech wymiarów.
4.1. Symulacja ciągła i symulacja zdarzeń dyskretnych
Zdarzenie dyskretne jest to chwilowa (migawkowa) operacja pojawiająca się w pewnym, wyjątkowym momencie czasu. Wyróżnienie w systemie tego typu zdarzeń pomaga przyjęcie pewnych przedziałów czasowych. w których pojawiły się istotne zmiany stanu systemu. Samolot lądujący na płytę lotniska, cześć docierająca do miejsca obróbki, klient wchodzący do banku są to wszystko przykłady zdarzeń dyskretnych.
Zdarzenie ciągłe jest to takie działanie, które trwa bez przerw. Ciągłość zdarzenia nie jest, tak jak w przypadku zdarzeń dyskretnych, przerywana jakimiś chwilowymi operacjami. Rosnąca cały dzien., a potem spadająca nocą temperatura wody w jeziorze, przepompowywanie paliwa do tankowca oto proste przykłady zdarzeń ciągłych, które zazwyczaj opisać można stosując tempo zmian (np. litr/godzinę).
Poniższy rysunek przedstawia w sposób graficzny różnicę między zdarzeniem dyskretnym, a zdarzeniem ciągłym.
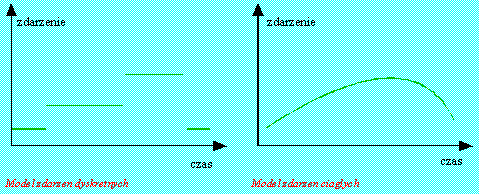
Rys 2. Zdarzenia dyskretne i ciągłe
Oczywiście w praktyce trudno jest znaleźć system, którego zdarzenia byłyby całkowicie ciągłe, czy całkowicie dyskretne, ale zazwyczaj można stwierdzić, która z charakterystyk (ciągła czy dyskretna) dominuje w badanym systemie.
4.2. Statyczne i dynamiczne modele symulacyjne
Statyczny model symulacyjny to taki model, w którym zmiana czasu nie ma wpływu na wynik eksperymentu, czyli upływanie godzin, minut, sekund, nie odgrywa żadnej roli. Dobrym przykładem jest model symulacyjny opisujący rzut kostka. Wynik (1,2,3,4,5 lub 6) nie jest w żaden sposób uzależniony od czasu. Przykładem metod symulacyjnych dla modeli statycznych jest metoda Monte Carlo.
Dynamiczne modele symulacyjne to modele, na które upływ czasu ma istotny wpływ. Stan modelu zmienia się stopniowo wraz z upływem sekund, minut, godzin.
4.3. Stochastyczne i deterministyczne modele symulacyjne
Symulacja stochastyczna opiera się na procesach stochastycznych, to znaczy takich, które zbudowane są z sekwencji losowo generowanych wartości. Okresy czasów pomiędzy momentami, kiedy psuje się maszyna, czy tez czasy potrzebne do jej naprawy to przykłady procesów stochastycznych. Wartości (czasy) zmieniają się w sposób losowy i wymagają zastosowania metod z zakresu rachunku prawdopodobieństwa.
Modele symulacji deterministycznej to takie modele, w których nie wykorzystuje się losowych zdarzeń. Oznacza to, ze przebieg eksperymentu symulacyjnego nie podlega prawdopodobieństwa.
5. Klasyfikacja narzędzi symulacyjnych. Wybór narzędzia, przy pomocy, którego realizowany jest eksperyment symulacyjny jest bardzo istotny i zależy od wielu czynników: doświadczenia modelującego, specyfiki problemu, wymaganego poziomu dokładności itp.
Poniższa tabela przedstawia cztery klasy narzędzi symulacyjnych.
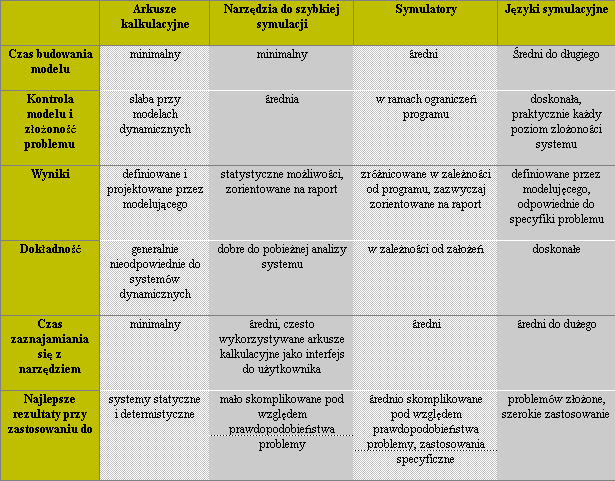
5.1. Arkusze Kalkulacyjne Pierwsza kategorie w powyższej tabeli stanowią arkusze kalkulacyjne (Spreadsheets) takie jak: LOTUS 1-2-3, EXCEL etc., Chociaż na ogol nie są one znane ze swych możliwości symulacyjnych, to jest jednak możliwe wykonanie eksperymentu symulacyjnego przy użyciu funkcji, występującej praktycznie w każdym arkuszu kalkulacyjnym, generującej liczby losowe (w większości narzędzi jest to funkcja”@RAND” lub podobna).
Budowanie eksperymentu symulacyjnego przy użyciu arkuszy kalkulacyjnych zabiera minimalna ilość czasu. Częste przykłady zastosowań arkuszy kalkulacyjnych jako narzędzi symulacyjnych można znaleźć np. w bankowości, gdzie wykorzystywane są do określania spodziewanych zysków, analizy portfela inwestycyjnego itp.
Arkusze kalkulacyjne pozwalają na zaprezentowanie wyników w formie graficznej (wykresy), czy tez w postaci tabel. Daje to możliwość szybkiej analizy problemu, co w świecie współczesnego biznesu jest wielka zaleta. Należy jednak pamiętać, ze zastosowanie arkuszy kalkulacyjnych ogranicza się jedynie do symulacji systemów statycznych.
5.2. Narzędzia do “szybkiej” symulacji Kolejna kolumnę w powyższej tabeli zajmują tzw. narzędzia do “szybkiej” symulacji (rapid modelling tools), do których zaliczyć można ManuPlan/SimStarter. Zadaniem tych narzędzi jest szybka ocena takich zagadnień jak przepustowość czy wąskie gardła w procesie produkcyjnym. Zazwyczaj symulacja przy użyciu tych narzędzi ogranicza się do analizy najistotniejszych elementów badanego systemu. W wielu przypadkach, określony z grubsza wynik, jest wystarczający, kiedy na stawiane pytania wymagana była szybka odpowiedz.
5.3. Symulatory Symulatory są to programy, pozwalające na szybka budowę modeli symulacyjnych specyficznych zagadnień. Przykładem może być SLAM II. Jest to program przeznaczony do symulacji przede wszystkim systemów produkcyjnych, gdzie znajdują się predefiniowane elementy, które ograniczają role modelującego jedynie do logicznego połączenia tych elementów i dostarczenia danych do obróbki. Symulatory nie wymagają praktycznie żadnych umiejętności z zakresu programowania, choć należy zaznaczyć, ze można często poszerzyć możliwości stosowanego programu poprzez uzupełnienie dodatkowym kodem. Zazwyczaj symulatory zapewniają atrakcyjna prezentacje wyników w postaci graficznej. Umożliwiają one tez często eksportowanie zbiorów z wynikami symulacji do innych programów graficznych. Należy jednak pamiętać, ze symulowanie innych problemów, niż te określone przez producenta, jest z reguły niemożliwe.
Symulatory nie wymagają długiego okresu przeszkolenia i przeważnie kilka dni wystarcza, aby samemu zbudować eksperyment symulacyjny.
5.4. Języki symulacyjne Ostatnia kolumna w powyższej tabeli odnosi się do Języków Symulacyjnych. W praktyce spotyka się języki programowania o ogólnym zastosowaniu (Pascal, C++, itd.), które również mogą być zastosowane, do budowania eksperymentów symulacyjnych. Zdarza się, tak jak jest to w przypadku programu SlamSystem, posiadającego typowe cechy symulatora (predefiniowane elementy), ze można tworzyć dodatkowe aplikacje używając języków ogólnego zastosowania (w przypadku SlamSystem jest to Fortran).
Na rynku dostępne są także języki programowania, których zastosowanie ogranicza się przede wszystkim do rozwiązywania problemów symulacyjnych. Jako przykłady mogą służyć SIMAN - język do symulacji systemów produkcyjnych (SIMulation ANalysis program), czy GPSS (General Purpose Simulation System) - język przeznaczony do wybranych typów symulacji zdarzeń dyskretnych. Inne popularne języki symulacyjne to SIMSCRIPT i SIMULA.
Zastosowanie języków symulacyjnych pozwala na bardzo szczegółowe badanie analizowanych modeli, co w przypadku wyżej wspomnianych narzędzi jest utrudnione, ze względu na ich z góry określoną specyfikę zastosowań. Wada ich jest natomiast to, ze próby rozwiązania nawet stosunkowo prostych problemów wymagają długiego okresu czasu i podstawowej wiedzy z zakresu programowania.
Należy pamiętać, ze wszelkie klasyfikacje staja się utrudnione wraz z rozwojem technik symulacyjnych, gdyż wszystkie poszczególne klasy przenikają się nawzajem. Możliwe są także bardziej szczegółowe podziały narzędzi symulacyjnych, np. w ramach symulatorów często w literaturze wyróżnia się:
“czyste” symulatory
symulatory z możliwością programowania
A w przypadku języków symulacyjnych:
Języki symulacyjne z pewnymi elementami symulatorów
Języki symulacyjne
Przykłady innych symulatorów:
Symulator samolotu PZL-130 "Orlik"
Symulator ten jest wyposażony w trzykanałowy system wizualizacji z generatorem obrazu najnowszej generacji. Pole widzenia z kabiny pilota zawiera się w obszarze 30× 115 stopni. Generowany jest obraz otoczenia samolotu z możliwością zmiany warunków atmosferycznych, widzialności, pory dnia i pory roku. Poza tym symulator zapewnia: pełną symulację dźwięku (szumy aerodynamiczne, praca silnika, systemy pokładowe), symulację pracy instalacji i wskazań przyrządów pokładowych, imitację obciążenia na organach sterowania, symulacje awarii oraz niesprawności instalacji i urządzeń pokładowych, wprowadzanie dowolnych warunków szkolenia przy budowaniu scenariusza lotu. Opcjonalnie symulator może być wyposażony w platformę o 3 lub 6 stopniach swobody.
Symulator kolejowy
Nie tylko umiejętność pilotowania samolotów może być ćwiczona na symulatorach. Kompleksowy symulator loko-motywy elektrycznej wykorzystywany jest do szkolenia maszynistów kolejowych pociągów pasażerskich i towarowych. W symulatorze zastosowano system komputerowej generacji obrazu (CGI). Dzięki temu obraz widziany przez przednią szybę kabiny jest zbliżony do rzeczywistego, włącznie z symulacją warunków atmosferycznych, pory roku i doby. Układ ruchu o 6 stopniach swobody zapewnia odwzorowanie wszelkich odczuć pochodzących od prze-ciążeń, jakie występują w czasie rzeczywistej jazdy (łącznie z oddziaływaniem lokomotywy ze składem wagonów). Zapewniona jest pełna symulacja efektów dźwiękowych słyszalnych wewnątrz rzeczywistej kabiny lokomotywy oraz symulacja pracy instalacji i wskazań wszystkich przyrządów. Oprogramowanie umożliwia zmianę oznakowania linii kolejowej, ustawiania nieruchomych przeszkód na torze oraz ruchomych obiektów na przejazdach z możliwością symulacji kolizji z tymi przeszkodami. W tym wirtualnym środowisku można umieszczać "pociągi widma" dla zainscenizowania wszelkich normalnych i nienormalnych sytuacji ruchowych łącznie z katastrofami.
Symulator samolotu TS-11 "Iskra"
Symulator ten jest urządzeniem klasy "full-mission", służącym do szkolenia i treningu pilotów w pełnym zakresie pilotażu, do trenowania ich zachowań w sytuacjach awaryjnych oraz związanych z wykorzystaniem uzbrojenia. Kabina wyposażona została w imitator wszystkich przyrządów pilotażowo-nawigacyjnych i sterownic. Trójkanałowy, kolimatorowy system wizualizacji wykorzystuje generator obrazu CGI na bazie grafiki XS-24Z Silicon Graphics o rozdzielczości 1280×1024 z możliwością wprowadzania różnych warunków atmosferycznych, pory roku i dnia oraz generowania obiektów ruchomych. Dźwięk symulowany jest przez generator klasy Hi-fi. Odtwarzane są wszystkie dźwięki związane z pracą silnika, szumami aerodynamicznymi, pracą instalacji i urządzeń pokładowych. Symulację sił na organach sterowania zapewnia układ hydrauliczny sterowany cyfrowo o dokładności odtwarzania charakterystyk 5 proc. Symulator przystosowany jest do zabudowy na ruchomej platformie o 3 lub 6 stopniach swobody.
Wyszukiwarka
Podobne podstrony:
SYMULACJA
mgr cw 2 symulacja zmian stanu zasobów 2010
prognozowanie i symulacje wyklad (25 str)
Nabici w kapsułę – bezsens treningów polskich pilotów na rosyjskich symulatorach
Środowisko programowe do symulacji zjawiska tunelowania
,Modelowanie i symulacja system Nieznany (3)
Uczenie się przez symulację, PEDAGOGIKA, Metodyka nauczania przedmiotów pedagogicznych
Program - PROGNOZOWANIE I SYMULACJA, STUDIA, prognozowanie
prognozowanie i symulacje
projekt symulacje pspice polak
SYMULACJA KOMPUTEROWA OBWODÓW ELEKTRYCZNYCH
M5 Modelowanie i symulacja silnika wrzecionowego SM
Dane do symulacji dyszy Bedemanna
Metody symulacji zadanie 8
20030819 Ściany1
Prognozowanie i symulacje wykład 1 2010
prognozowanie i symulacje-ściąga, Ekonomia
opis symulacji 3, Nieruchomości, Nieruchomości - pośrednik
więcej podobnych podstron