Prognozowanie

i symulacje 

Dr inż. Paweł Najechalski

Literatura

• Polscy prekursorzy Zbigniew Czerwioski, Zdzisław Hellwig…
• Prognozowanie gospodarcze. Metody i zastosowania, M. Cieślak (red.), 

PWN, Warszawa 2005

• A. Zeliaś, B. Pawełek, S. Wanat , Prognozowanie ekonomiczne. Teoria, 

przykłady, zadania, PWN, Warszawa 2003

• Prognozowanie gospodarcze. Metody, modele, zastosowania, przykłady, 

E. Nowak (red.), Ag. Wyd. Placet, Warszwa 1998

• B. Guzik, Wstęp do teorii prognozowania i symulacji, Wyd. AE w 

Poznaniu, Poznao 2008

• J. B. Gajda, Prognozowanie i symulacje a decyzje gospodarcze, Wyd. C.H. 

Beck, Warszawa 2001

• Metody prognozowania. Zbiór zadao, B. Radzikowska (red.), Wyd. AE we 

Wrocławiu, Wrocław 1999

• M. Witkowski, T. Klimanek, Prognozowanie gospodarcze 

i symulacje w przykładach i zadaniach, Wyd. AE w Poznaniu, Poznao 

2007

WSHiP

dr inż. Paweł Najechalski

2

Pojęcie prognozy

• Przewidywanie jest wnioskowaniem o 

zdarzeniu nieznanym na podstawie zdarzeo 
znanych

• Prognozowanie (predykcja) jest 

przewidywaniem opartym na metodach 
naukowych przyszłych zdarzeo i określa:

co będzie w momencie t

WSHiP

dr inż. Paweł Najechalski

3

Pojęcie symulacji

• Symulacja jest niepewnym sądem o zjawisku 

uzyskanym dla różnych wariantów, czyli 
odpowiada na pytanie:

co by było gdyby…

WSHiP

dr inż. Paweł Najechalski

4

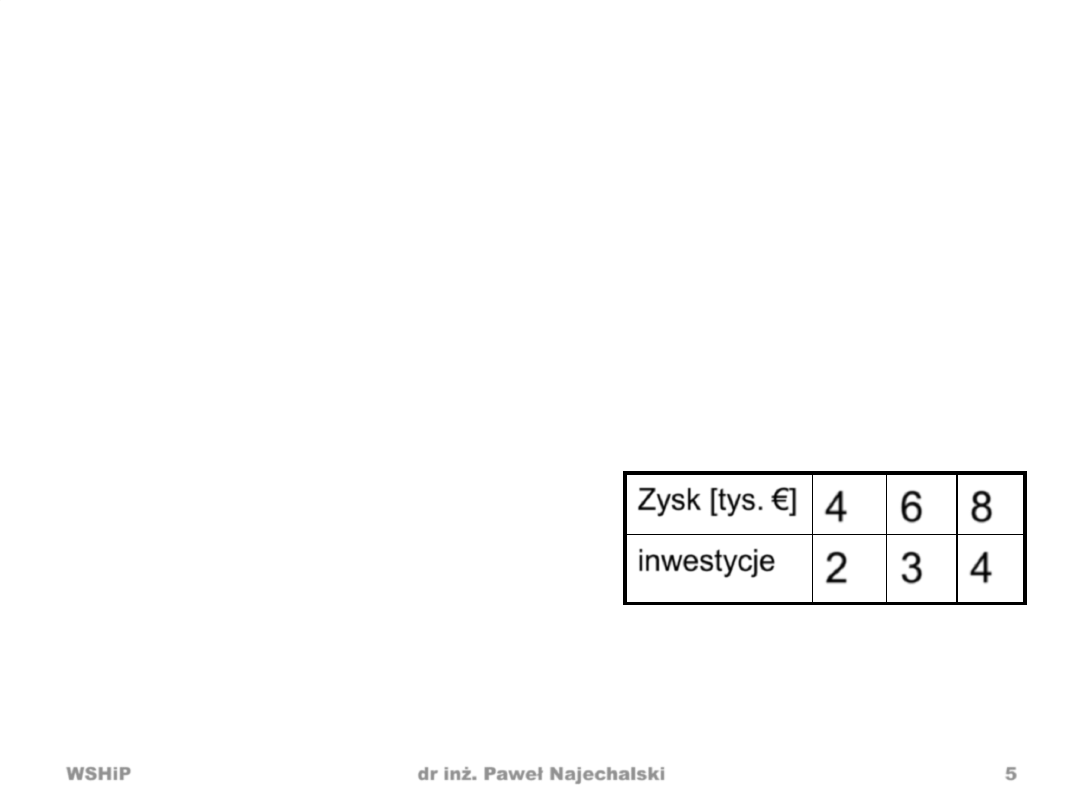
Przykład prognozy i symulacji

• W miesiącu maju  

firma osiągnie  zysk 
10 tys. €

• Wartośd inwestycji: 

50%



z 10 tys. € =  5 

tys. €

• PROGNOZA

• Wartości inwestycji w 

maju przy różnych 
wielkościach zysku 

• SYMULACJA

WSHiP

dr inż. Paweł Najechalski

5

Firma ProgSym 50% miesięcznego zysku 
inwestuje w papiery wartościowe.

Zysk [tys. 

€]

4

6

8

inwestycje

2

3

4

Podział prognoz

ze względu na

• Rodzaj metody prognozowania

• Wartośd prognozy

• Okres prognozy

WSHiP

dr inż. Paweł Najechalski

6

Metody prognozowania

• Proste i intuicyjne – prognozowanie status 

quo

(na podstawie prostych charakterystyk ilościowych)

• Modelowe   

(modele ekonometryczne, adaptacyjne)

• Analogowe

(poprzez analogię)

• Heurystyczne 

(prognozy ekspertów)

• Scenariuszowe 

(wyznaczanie różnych scenariuszy rozwoju zjawiska)

WSHiP

dr inż. Paweł Najechalski

7

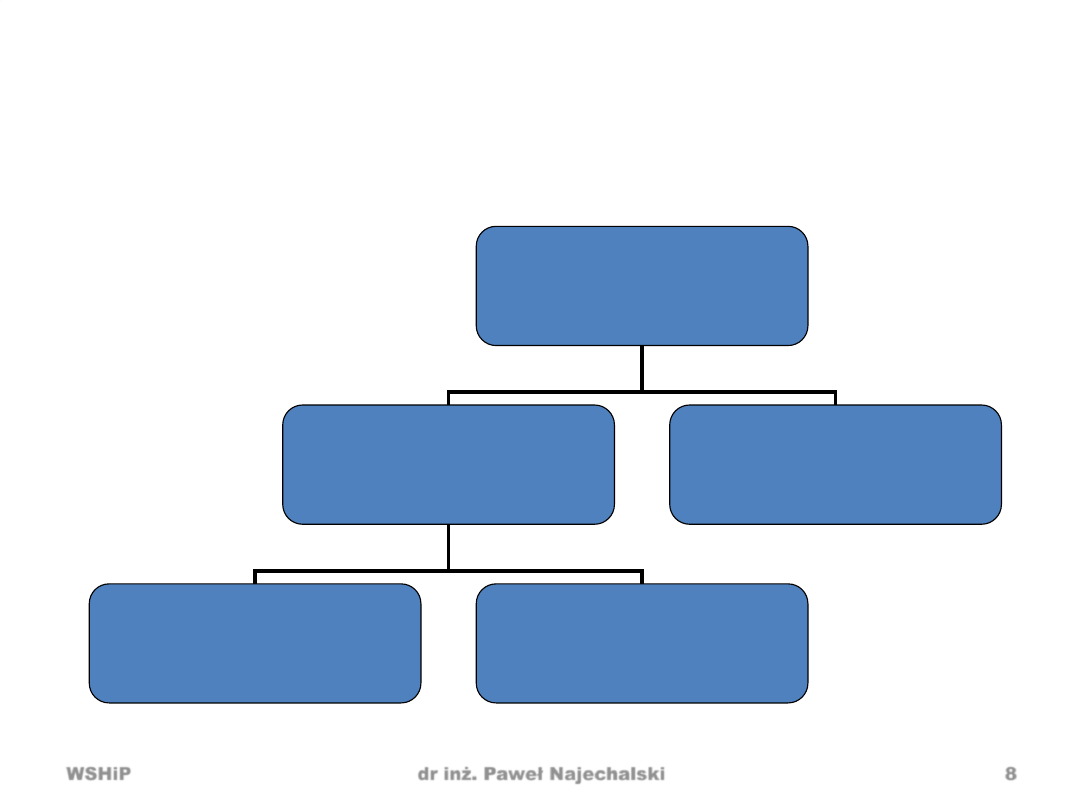
Uproszczona klasyfikacja prognoz

prognozy

ilościowe

jakościowe

punktowe

przedziałowe

WSHiP

dr inż. Paweł Najechalski

8

Okres prognozy

• Krótkookresowe

-

zachodzą tylko zmiany ilościowe

* zasięg ekstrapolacji (liczba jednostek czasu wyjścia z prognozą w 
przyszłośd) stanowi do 10% liczby danych n

• Średniookresowe

- zachodzą zmiany ilościowe i niewielkie zmiany jakościowe
* zasięg ekstrapolacji stanowi do 10% do 20% liczby danych n

• Długookresowe

- zachodzą zmiany ilościowe i jakościowe
* zasięg ekstrapolacji stanowi powyżej 20% liczby danych n

WSHiP

dr inż. Paweł Najechalski

9

Kryteria doboru danych

•

Rzetelnośd:

zgodnośd z przedmiotem, którego dotyczą

(występowanie błędów losowych i systematycznych)

•

Jednoznacznośd:

jednoznaczny sposób interpretowania danych

•

Identyfikowalnośd:

wiele zjawisk można opisad przy użyciu różnych zmiennych

•

Kompletnośd:

uwzględnienie wszystkich ważnych informacji dla problemu

•

Aktualnośd danych dla przyszłości:

określenie siły 

czynników istotnych w przyszłości (fakty niosące przyszłośd)

•

Koszt zbierania

i 

opracowywania danych:

dążenie do minimalizacji liczby danych

•

Porównywalnośd danych:

uzyskanie porównywalności: 

czasowej, terytorialnej, pojęd i kategorii, metod obliczeo

WSHiP

dr inż. Paweł Najechalski

10

Etapy prognozowania

1. Sformułowanie zadania prognostycznego 

Określenie: obiektu, zjawiska, 

zmiennych, celu, warunków dopuszczalności, horyzontu prognozy

2. Określenie przesłanek prognostycznych 

Postawienie hipotez odnośnie 

czynników kształtujących zjawisko, deklaracja prognosty co do postawy wobec 

przyszłości zjawiska, ustalenie zbioru danych potrzebnych do prognozy, zbieranie 

danych

3. Wybór metody prognozowania

Na bazie przesłanek prognostycznych: postawa 

pasywna – prognozowanie na podstawie szeregów czasowych, prognozowanie 

ekonometryczne ze stałymi parametrami; postawa aktywna – prognozowanie 

symulacyjne, ekonometryczne ze zmiennymi parametrami, analogowe, heurystyczne

4. Wyznaczenie prognozy  Schemat obliczeniowy metody, decyzje w sytuacjach 

trudnych prognozowania, założenia, kryteria, wartości krytyczne.

5. Ocena dopuszczalności prognozy

Zgodnośd z wymogami odbiorcy: błąd prognozy 

ex ante, horyzont dopuszczalności, zmiana wymagao jakościowych prognozy

6. Wykorzystanie  prognozy Podjęcie decyzji
7. Weryfikacja prognozy

Określenie trafności prognozy: błąd prognozy ex 

post, analiza słuszności postępowania prognostycznego, określenie przyczyn błędu w 

prognozowaniu, systematycznośd weryfikacji (monitoring)

WSHiP

dr inż. Paweł Najechalski

11

Podstawowe oznaczenia

Y – zmienna prognozowana (predykata)
X – zmienna niezależna (objaśniająca, predyktanta)
n – liczba obserwacji
y

t

– wartośd zmiennej Y w obserwacji o numerze t, t = 1,…,n

y

t

*

– prognoza dla obserwacji t (prognoza wartości y

t

)



t – moment, na który formułowana jest prognoza 

(gdy t > n można oznaczad moment przez 



=n+1, n+2, …, T)

T – ostatni moment (punkt) dla którego sformułowano 

prognozę

WSHiP

dr inż. Paweł Najechalski

12

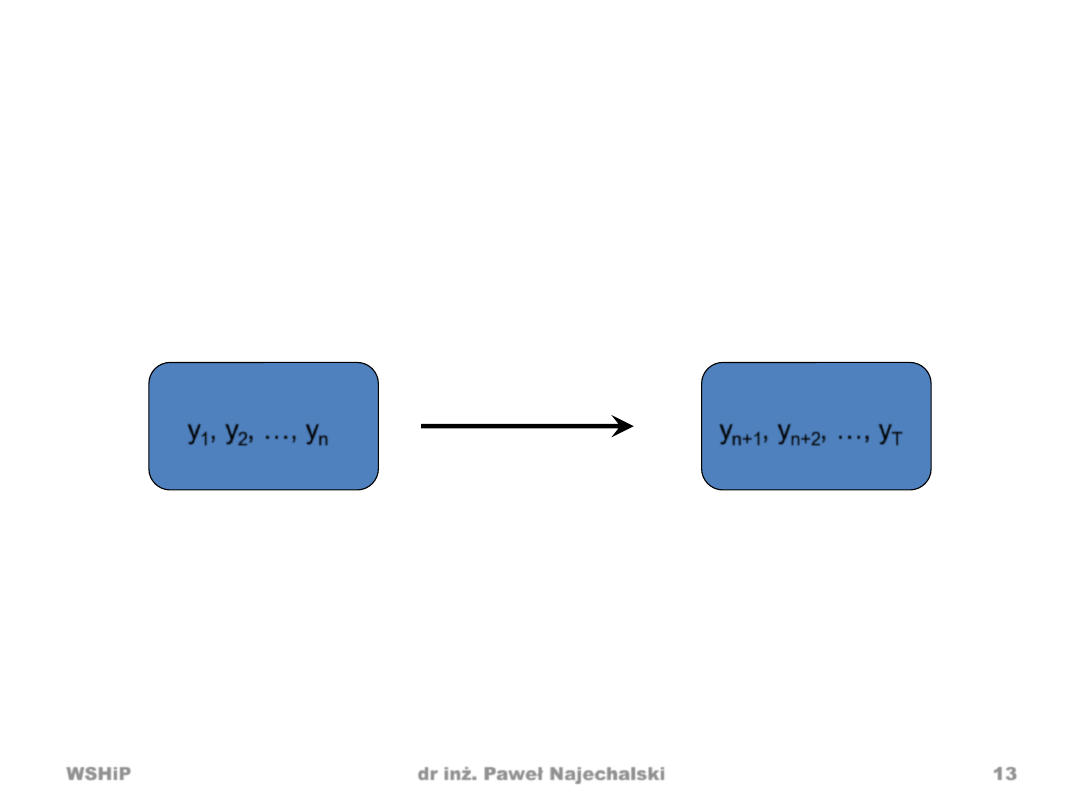
Ogólny schemat prognozowania

• przypadek jednowymiarowego szeregu 

czasowego

WSHiP

dr inż. Paweł Najechalski

13

y

1

, y

2

, …, y

n

y

n+1

, y

n+2

, …, y

T

przeszłość

przyszłość

MODEL

reguła 

prognozowania 

Przyczyny błędów prognoz

• Wybór metody prognozowania
• Dobór postaci analitycznej modelu 
• Dobór listy zmiennych objaśniających
• Estymacja parametrów modelu
• Wybór wartości zmiennych objaśniających
• Działanie czynników losowych
• Opóźnienie prognoz w stosunku do y

t

WSHiP

dr inż. Paweł Najechalski

14

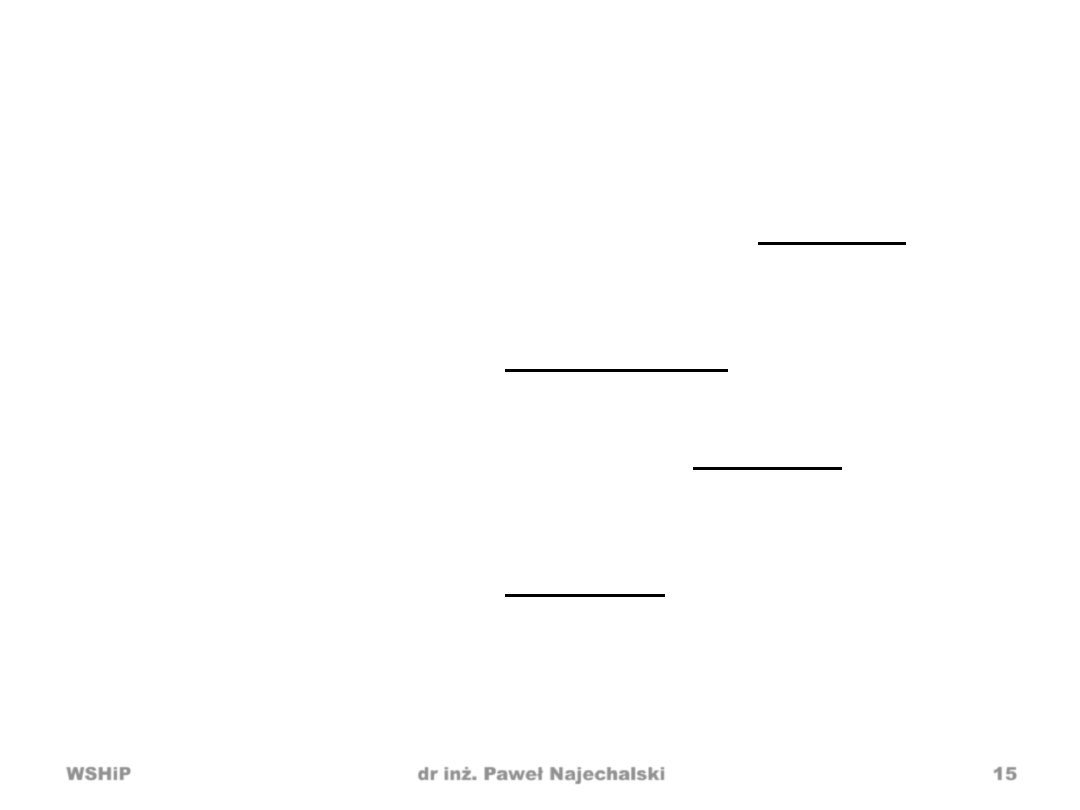
Jakośd prognoz ex ante i  ex post 

• Błąd prognozy ex ante:

miernik

szacowany przed realizacją prognozy, określa 
jakośd prognozy – dokładnośd

• Błąd prognozy ex post:

miernik

wyznaczany po realizacji prognozy, określa 
jakośd prognozy – trafnośd

WSHiP

dr inż. Paweł Najechalski

15

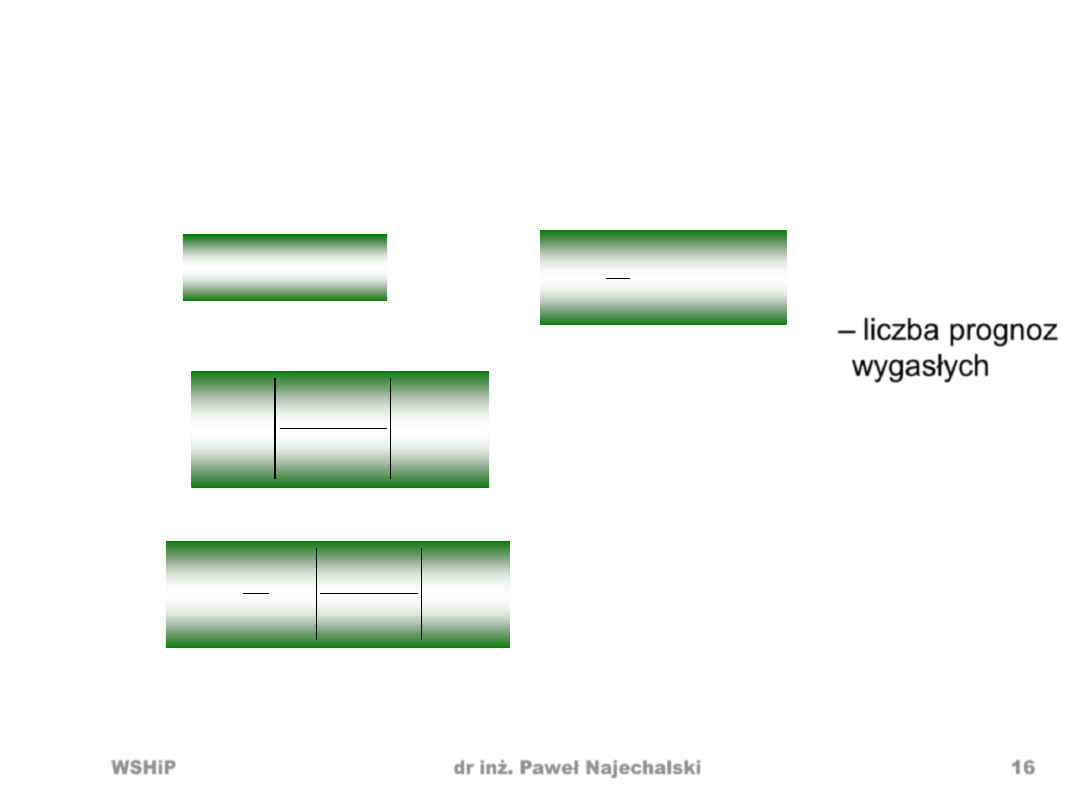
Błędy prognoz ex post

• Absolutny     i

średnia błędów absolutnych

• Względny „modułowy”

• Średni względny „modułowy”

*

t

t

t

y

y

q





WSHiP

dr inż. Paweł Najechalski

16

%

100

*

t

t

t

t

y

y

y







%

100

1

*









t

t

t

t

y

y

y

L











t

t

t

y

y

L

q

*

1

L – liczba prognoz 

wygasłych

Błąd prognoz ex post

• Średni kwadratowy

• Średni względny

• Współczynnik Theila 

WSHiP

dr inż. Paweł Najechalski

17







t

t

t

y

y

L

s

2

*

2

*

)

(

1

%

100

*

*

*

t

t

y

s

V















t

t

t

t

t

y

y

y

I

2

2

*

2

%

100

*

y

s

V



s

*

– średni błąd predykcji ex post 

(odchylenie standardowe prognozy)

L – liczba prognoz wygasłych

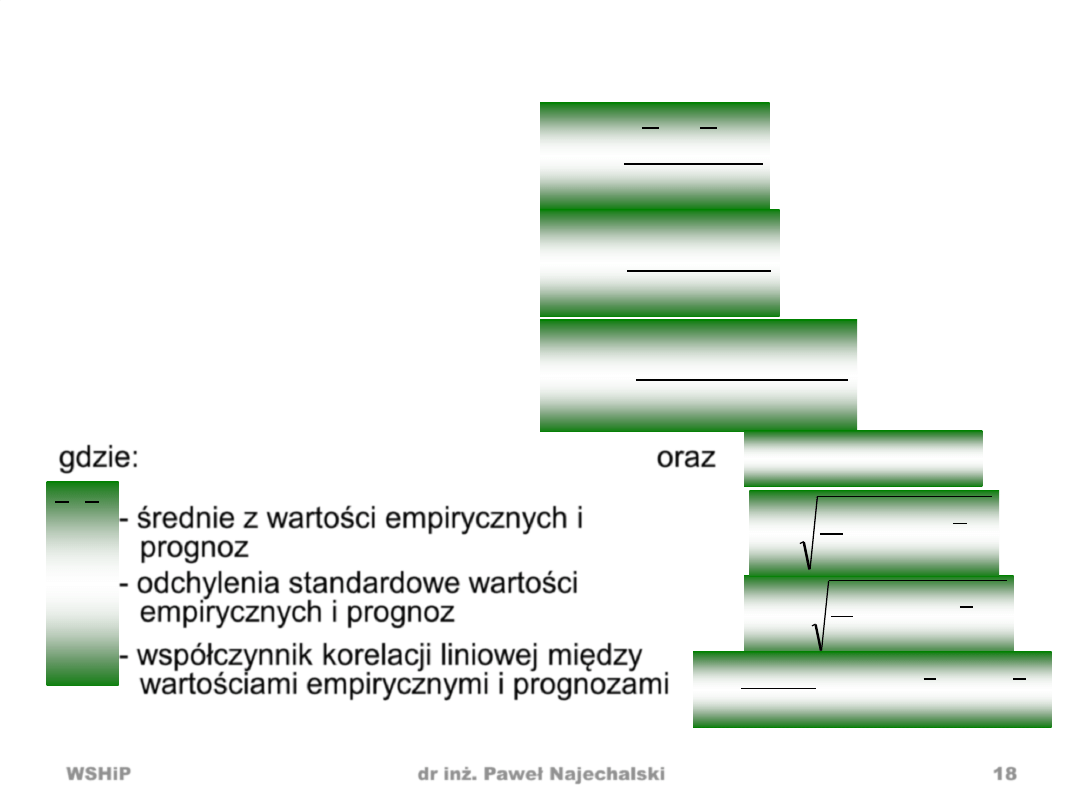
Wskaźniki przyczyn błędów wg H. Theila

• Udział obciążenia

• Udział nieelastyczności

• Udział niezgodności

kierunkowej

WSHiP

dr inż. Paweł Najechalski

18











t

t

y

y

L

s

2

*

*

*

*

1





2

*

2

*

2

1

ˆ

s

y

y

I









2

*

2

*

*

2

2

ˆ

s

s

s

I









2

*

*

*

2

3

1

2

ˆ

s

r

s

s

I





1

ˆ

ˆ

ˆ

2

3

2

2

2

1







I

I

I

r

s

s

y

y

*

*

*

,

,

-

średnie z wartości empirycznych i 

prognoz

-

odchylenia standardowe wartości 

empirycznych i prognoz

-

współczynnik korelacji liniowej między 

wartościami empirycznymi i prognozami

gdzie: 

oraz











t

t

y

y

L

s

2

1

















t

t

t

y

y

y

y

s

s

L

r

*

*

*

*

1

Klasyfikacja na podstawie trafności

Wartość miernika

Klasa prognozy

0 

– 3%

prognozy o dużej trafności

3 

– 6%

prognozy o dobrej  trafności

6 

– 10%

prognozy o dostatecznej trafności

powyżej 10%

prognozy o niedostatecznej 
trafności

WSHiP

dr inż. Paweł Najechalski

19

Powyższa klasyfikacja dotyczy błędów względnych

przede wszystkim „modułowych”.  Dopuszczalne

jest jej zastosowanie do innych błędów względnych.

Błędy prognoz ex ante

• Dla niektórych metod prognozowania nie ma 

możliwości oszacowania tego miernika 

• Wykorzystuje się stochastyczne założenia o 

mechanizmach generujących wartośd zmiennej 
prognozowanej

• Zakłada się m.in. że błąd prognozy jest zbliżony do 

średniej rozbieżności między możliwymi wartościami 
prognozowanego zjawiska a możliwymi prognozami 
tego zjawiska w okresie prognozy 

WSHiP

dr inż. Paweł Najechalski

20

Dopuszczalnośd prognoz

• Prognozę uznaje się za dopuszczalną, jeżeli miernik 

niedokładności prognozy nie jest większy od pewnej przyjętej 
wartości. W przypadku mierników względnych jest to przeważnie 
wartośd z zakresu 5-10%

• Jako granicę dopuszczalności prognozy przyjmiemy 6%
• Jako miernik niedokładności prognozy stosujemy błędy 

ex ante

• Możliwe jest wykorzystanie jako mierników niedokładności 

błędów ex-post. Błędy te powinny byd obliczone w oparciu o 
prognozy uzyskane według takiej samej procedury i dla takiego 
samego okresu jak prognozy niezrealizowane (autentyczne, 
niewygasłe) 

WSHiP

dr inż. Paweł Najechalski

21

Horyzont prognozy

• Przedział czasowy *n+1;T+, dla którego 

dopuszczalne jest prognozowanie na 
podstawie danej procedury prognozowania

Przykład n=10 lat błędy prognoz na najbliższe lata: 



11

=4%, 



12

=6%, 



13

=7%,  

Stosując kryterium 



t



6% stwierdzamy spełnienie kryterium dla 

momentów t=11 i 12. Horyzont prognozy jest przedziałem 
[11;12] o długości 2 lat

WSHiP

dr inż. Paweł Najechalski

22

Przykład – obliczenia błędów

Na podstawie danych wartości tygodniowego zysku osiąganego 
przez sklep internetowy w okresie 10 kolejnych tygodni 
oszacowano model, dla którego wyliczono prognozy punktowe 
7,8; 8,4; 9; 9,6; 10,2 *w tys. zł+ na kolejne 5 tygodni. Po 
uzyskanych realizacjach 7; 8; 6; 10; 9 zmiennej prognozowanej 
(wygaśnięciu prognoz) w badanym okresie należy 
przeprowadzid ocenę trafności wykonanej prognozy i 
zinterpretowad obliczone błędy.   

WSHiP

dr inż. Paweł Najechalski

23

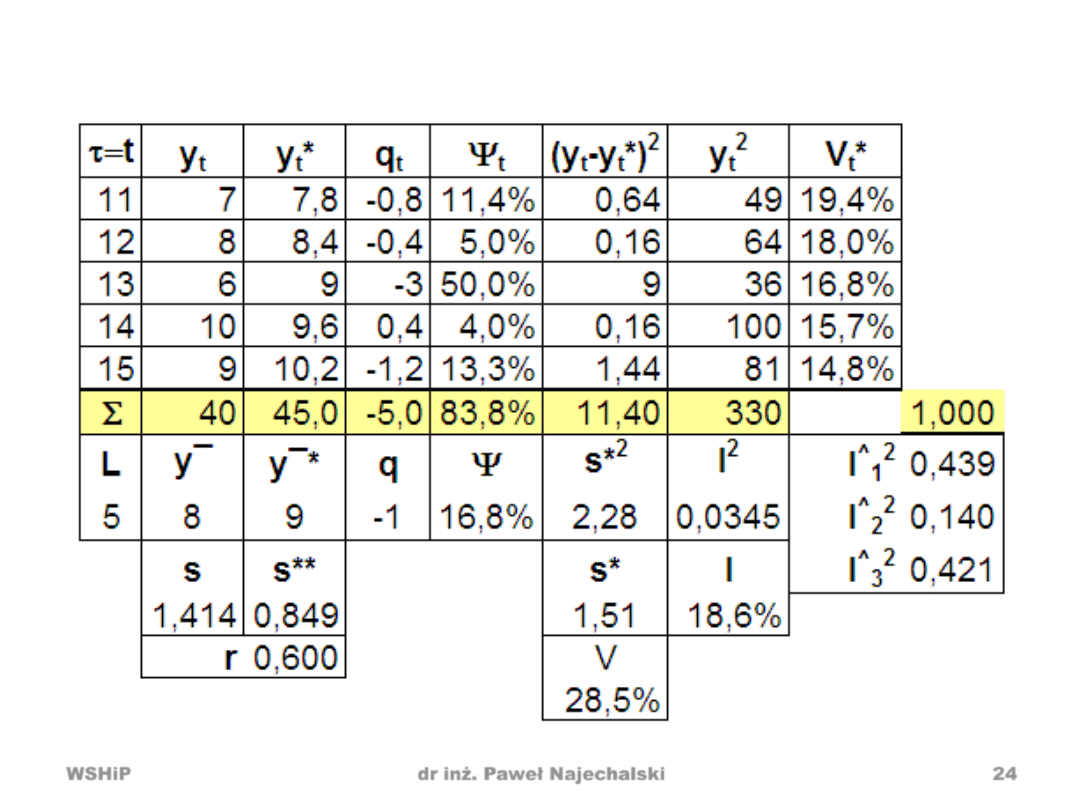
Obliczenia

WSHiP

dr inż. Paweł Najechalski

24

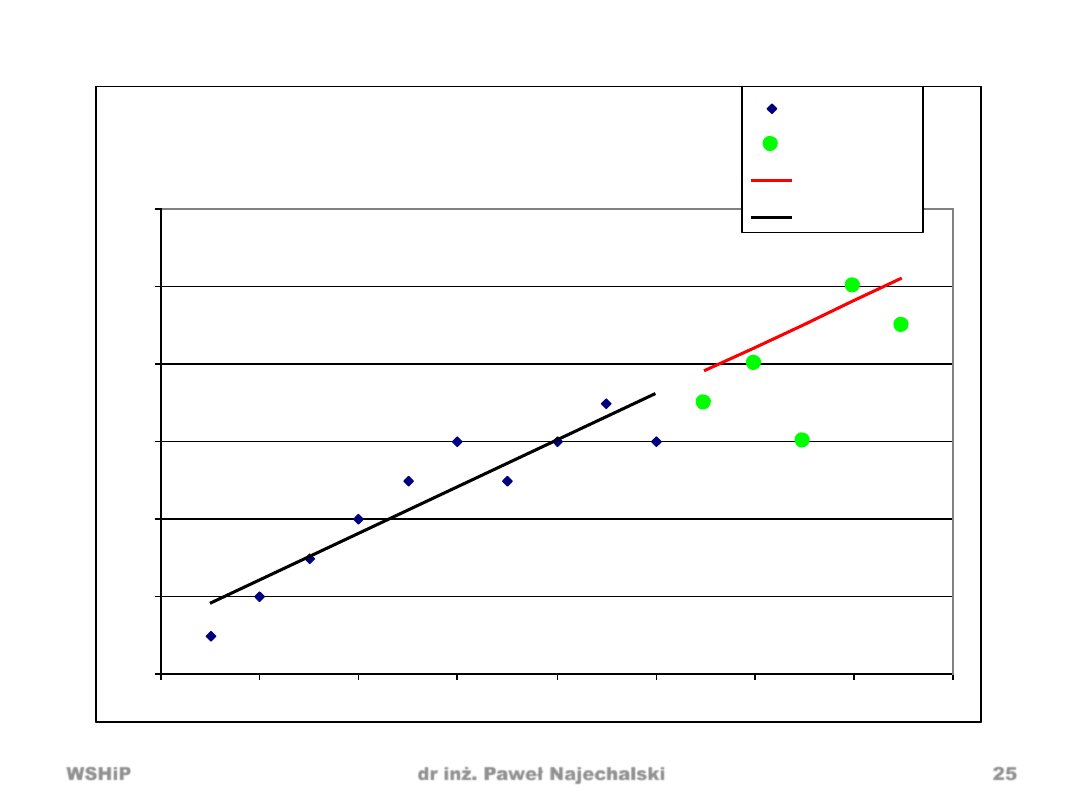
Wykres

WSHiP

dr inż. Paweł Najechalski

25

Sklep internetowy

y = 0,6x + 1,2

R

2

 = 0,8609

0

2

4

6

8

10

12

0

2

4

6

8

10

12

14

16

Tydzień t

Z

ys

k 

[t

ys

. z

ł]

yt

Realizacje

Prognoza

Liniowy (yt)

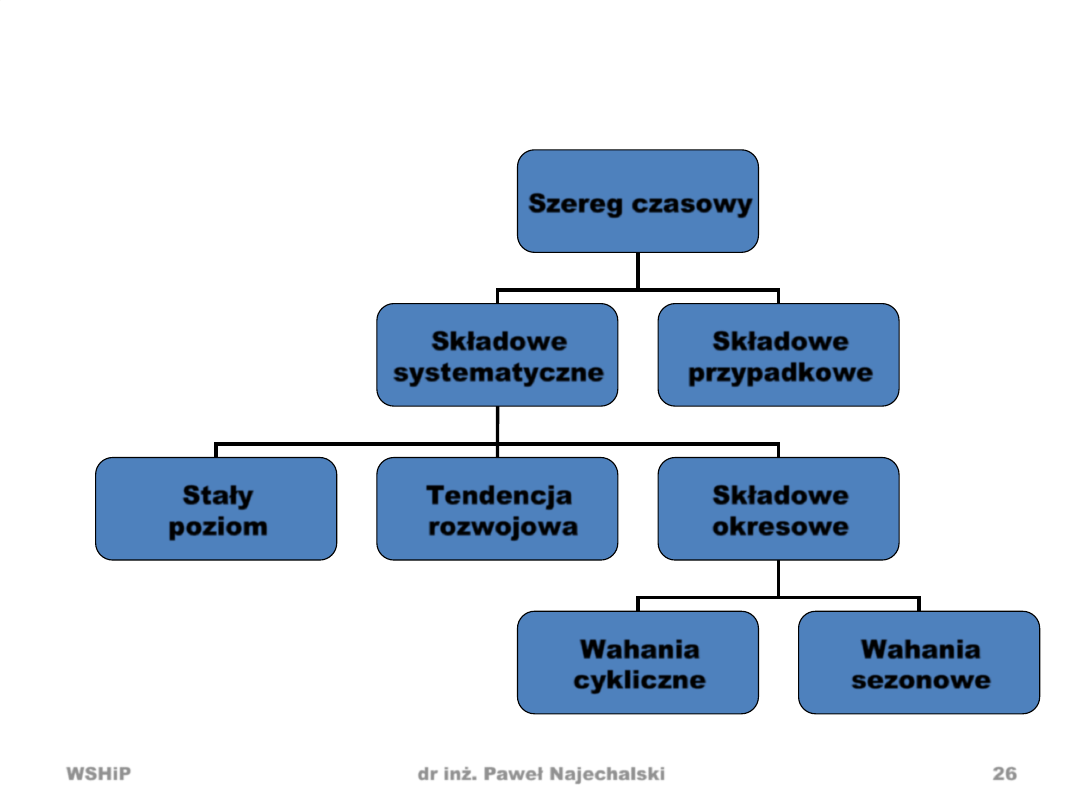
Składowe szeregów czasowych

Szereg czasowy

Składowe

systematyczne

Składowe

przypadkowe

Stały

poziom

Tendencja

rozwojowa

Składowe

okresowe

Wahania

cykliczne

Wahania

sezonowe

WSHiP

dr inż. Paweł Najechalski

26

Składowe szeregów czasowych

• przypadkowe (losowe) powstają na skutek działania przyczyn 

przypadkowych z różną siłą i w różnych kierunkach

• systematyczne powstają na skutek działania trwałego układu 

przyczyn i prawidłowości

• stały poziom zmiennej – obserwuje się oscylacje wokół pewnego 

poziomu, brak tendencji rozwojowej

• tendencja rozwojowa (trend) - określana jako długookresowa 

skłonnośd do jednokierunkowych zmian (wzrost lub spadek)

• wahania cykliczne – długookresowe wahania powtarzające się w 

okresie dłuższym niż 1 rok (z c. koniunkturalnym) 

• wahania sezonowe – wahania powtarzające się w okresie czasu nie 

przekraczającym 1 roku (z kalendarzem)

WSHiP

dr inż. Paweł Najechalski

27

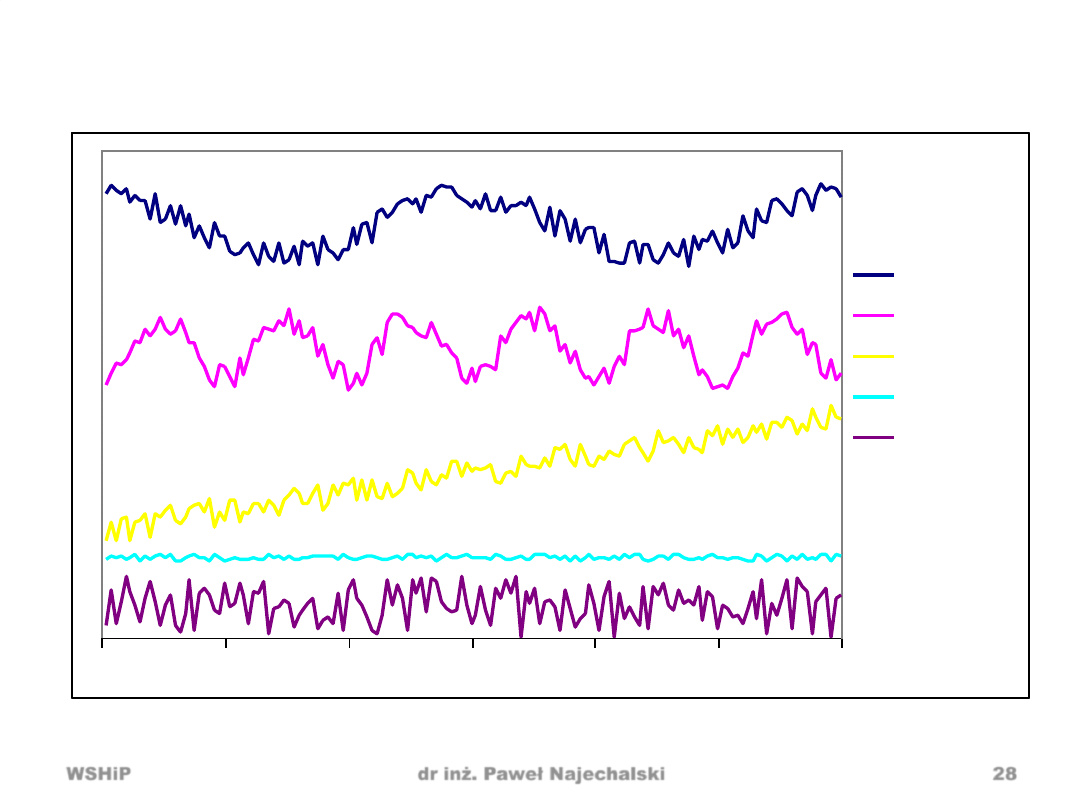
Składowe szeregów czasowych

0

1

2

3

4

5

6

Czas [w latach]

cykliczne

sezonowe

trend
stały

losowa

WSHiP

dr inż. Paweł Najechalski

28

Naiwne metody prognozowania

WSHiP

dr inż. Paweł Najechalski

29



wg stałego poziomu 

lub  



wg stałych przyrostów bezwzględnych 



wg stałych przyrostów względnych

1

*





t

t

y

y

3

3

2

1

*













t

t

t

t

y

y

y

y

2

1

2

1

1

*

2

)

(





















t

t

t

t

t

t

y

y

y

y

y

y

2

2

1

2

2

1

1

*

1

































t

t

t

t

t

t

t

y

y

y

y

y

y

y

Naiwne metody prognozowania

WSHiP

dr inż. Paweł Najechalski

30

r

y

y

r

y

y

y

r

t

r

t

r

t

t

r

2

1

1

...

...



























wg wahań sezonowych i stałego poziomu 



wg wahań sezonowych i trendu

gdzie 

-

przyrost średnich w dwóch ostatnich cyklach.

gdzie r

– długość okresu (liczba faz cyklu, sezonu)

r

t

t

y

y





*

r

r

t

t

y

y

y









*

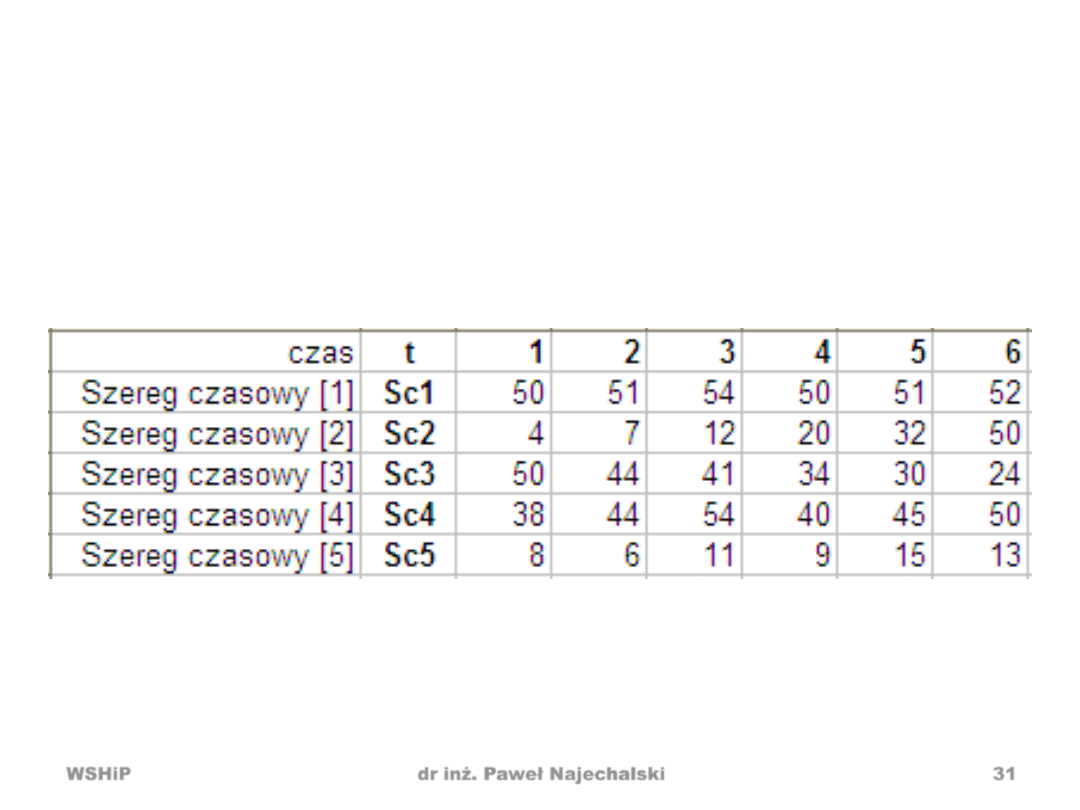
Przykład

Dla poszczególnych szeregów czasowych wyznaczyd 

prognozę naiwną dla t=7. Uzasadnid wybór metody.

WSHiP

dr inż. Paweł Najechalski

31

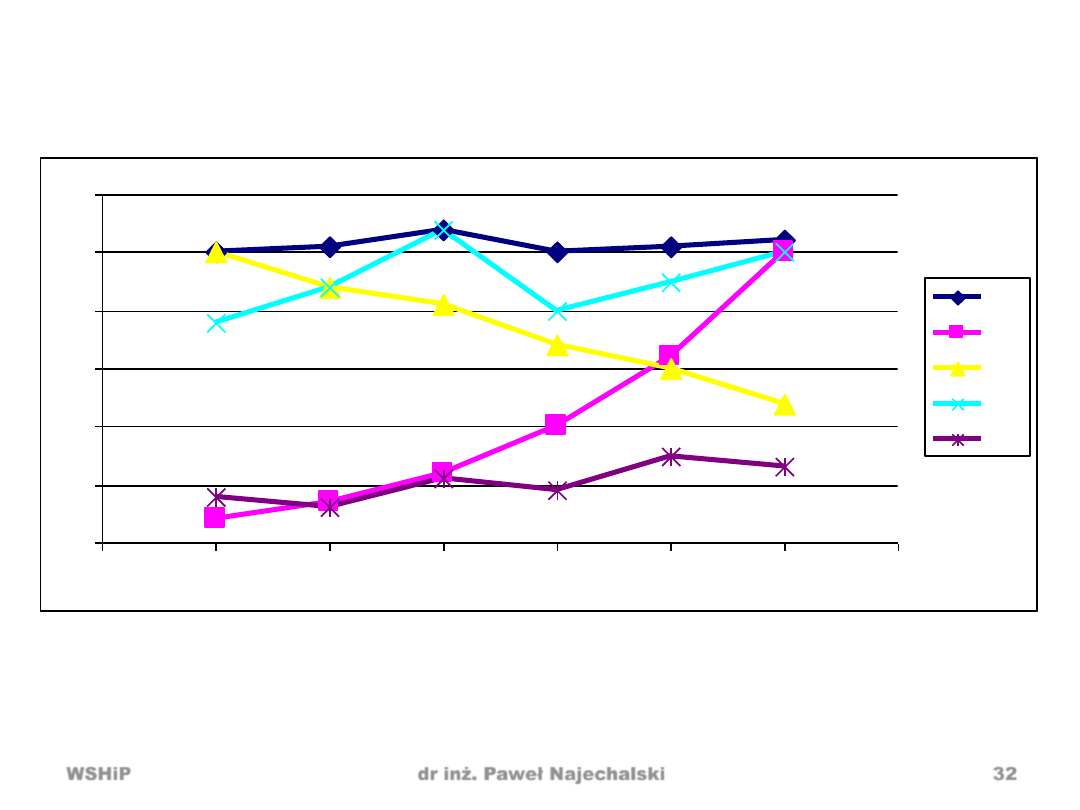
Wykresy szeregów czasowych

WSHiP

dr inż. Paweł Najechalski

32

0

10

20

30

40

50

60

0

1

2

3

4

5

6

7

Sc1

Sc2

Sc3

Sc4

Sc5