PROGNOZOWANIE I SYMULACJE MIEDZYNARODOWE

Maria Pociecha

Forma zaliczenia:

1/ praca kontrolna - w związku z metodami które będą przerabiane wcześniej (przed świętami na ostatnim spotkaniu na przygotowanych danych) później poda,

ocena na zaliczenie z pracy - tylko ocena „dobra” (dane dowolne praca, hobby-dane zaczerpnięte z własnej pracy zawodowej, z internetu, z rocznika statystycznego, dane obejmujące 10 okresów: 10 lat, 10 miesięcy, 10 dni); wykres danych - sporządzenie wykresu (funkcja liniowa)

2/ test - ostatni wykład - teoria

PROGNOZAOWANIE - przewidywanie, wnioskowanie o zdarzeniach nieznanych na podstawie zdarzeń znanych; przewidywanie może dotyczyć zdarzeń należących do przyszłości (przewidywanie), przewidywanie zdarzeń z przeszłości

Przewidywanie - racjonalne podejście, zdrowy rozsądek, naukowe oparte na zdrowym rozsądku przewidywanie przyszłości

PROGNOZOWANIE - sąd który charakteryzuję się: sąd sformułowany z wykorzystaniem dorobku nauki, odnoszący się do określonej przyszłości, weryfikowalny empirycznie (po upływie czasu na który prognoza została przewidziana); nasz sąd niepewny, akceptowalny,

Funkcje prognoz:

• preparacyjna - poprzez prognozowanie następuje wspomaganie procesów decyzyjnych w skali mikro i makro (dotyczy każdej sfery działalności), analiza gospodarki

• aktywizująca - polega na pobudzeniu do podejmowania działań które w efekcie sprzyjają realizacji prognozy

• informacyjne - wywoływanie określonych reakcji, akceptacja zmian)

Główne cele zastosowań prognoz:

• prognozowanie wielkości których nie można zaplanować

• prognozowanie wskaźników techniczno-ekonomicznych

• prognozowanie finansowe

• prognozowanie ścieżek rozwoju

• prognozowanie efektów zamierzonych posunięć gospodarczych

• prognozowanie stopnia realizacji przyjętych celów

• prognozowanie odchyleń od wyznaczonych celów

Metody prognostyczne:

Mat-statystyczne niematematyczne

Modele modele ankietowe

Deterministyczne ekonometryczne intuicyjne

intuicyjne

kolejnych przybliżeń

Jednorównaniowe wielorównaniowe ekspertyz

delficka

reflekscji

Klasyczne proste analogowe

Adaptacyjne rekurencyjne inne

Przyczynowo-opisowe o równaniach

Autoregresyjne współzależnych

SYMULACJA

Modele ekonometryczne mogą być również wykorzystane do symulacji, czyli badania możliwych stanów rzeczywistości za pomocą eksperymentowania na modelach.

Eksperymentowanie to polega na obliczeniu wartości zmiennej endogenicznej przy różnych, dopuszczalnych wartościach zmiennych objaśniających lub różnych wartościach parametrów. Symulację stosuję się m.in. wtedy, gdy zachodzi potrzeba rozpatrywania wielu wariantów przyszłości.

Klasyfikacja prognoz:

Kryterium podziału: sposób wyrażania stanu zmiennej

• prognoza ilościowa - punktowa lub podziałowa (np. km, zł, kg, konkretna kwota w danej jednostce czasu albo opiszemy przedział liczbowy np. dochód przedziału od...do...)

• prognoza jakościowa np. wykształcenie, płeć, wykonywany zawód, środowisko pochodzenia; skala nominalna lub porządkowa)

Kryterium podziału: horyzont czasowy tj. okres na który została zbudowana prognoza

• prognoza krótkookresowa - w tym podziale czasu zachodzą tylko zmiany ilościowe, sterowanie mało skuteczne

• prognoza średniookresowa - zachodzą zmiany ilościowe i niewielkie zmiany jakościowe, sterowanie jest możliwe

• prognoza długookresowa - występują zmiany ilościowe i znaczące jakościowe, sterowanie w szerokim zakresie

Kryterium podziału: charakter prognozy

• jednorazowe, powtarzalne

• kompleksowe i sekwencyjne

• samosprawdzające, destruktywne

• ogólne, szczegółowe

Kryterium podziału: zasięg terenowy

• światowe

• międzynarodowe

• krajowe

• regionalne

Dane w prognozowaniu:

Prawomocność procesu wnioskowania o przyszłości jest określana przez zdolność prognosty do rozpoznawania właściwego zasobu informacji o prognozowanym zjawisku i umiejętności wykorzystania tego zasobu do sformułowania prognozy

W procesie prognozowania wykorzystuję się dane:

• wewnętrzne, które są gromadzone w obiekcie na potrzeby zarządzania tym obiektem

• zewnętrzne - dot. Bliższego oraz dalszego otoczenia tworzącego ogólne warunki funkcjonowania obiektu

• wynikające z teorii dot. Prognozowanego zjawiska

Kryterium selekcji danych:

• rzetelność - dane powinny być zgodne z przedmiotem którego dotyczą

• jednoznaczne

• identyfikalność zjawiska przez zmianę

• kompletność

• aktualność danych dla przyszłości

• porównywalność danych

• koszt zebrania i opracowania danych

Przegląd metod prognozowania

Metoda prognozowania obejmuję sposób przetwarzania danych o przeszłości oraz sposób przejścia od danych przetworzonych do prognozy

Sposób przejścia od danych przetworzonych do prognozy nazywany jest REGUŁĄ PROGNOZY

Reguły prognozy (4):

1/ reguła podstawowa

prognozą jest stan zmiennej prognozowanej w należącym do przyszłości momencie lub okresie „t” otrzymany z modelu przy przyjęciu założenia że będzie on aktualny w chwili, na którą określa się prognozę

w przypadku klasycznego modelu regresji liniowej reguła podstawowa prognozy przybiera postać prognozy nieobciążonej. Prognoza jest wartością oczekiwaną zmiennej „Y” w momencie lub okresie „t>n”

y_t^* = E (y_t) t>n

gdzie: y_t^* jest prognozą, E (y_t) wartością oczekiwaną

2/ reguła podstawowa z poprawką

korzysta się z tej reguły gdy występuje uzasadnione przypuszczenia, że ostatnio zaobserwowane odchylenia od modelu utrzymują się w przyszłości:

y_t^* = E (y_t) + p t>n

gdzie: p - to poprawka dla t>n

p = Yn - Yn

3/ reguła największego prawdopodobieństwa (często się powtarza=modalna)

prognozą jest stan zmiennej, któremu odpowiada najwyższe prawdopodobieństwo lub maksymalna wartość funkcji gęstości rozkładu (wartość modalna rozkładu)

reguła ta jest naturalna, gdy zmienna prognozowa jest skokowa (np. liczba osób, wyjazd na wczasy) lub niemierzalna (jakościowa) np. wykształcenie, zawód

4/ reguła minimalnej straty

prognozą jest taki stan zmiennej, którego realizacją spowoduje minimalne straty. Przyjmuje się, że wielkość straty jest funkcją błędu prognozy i poszukuje się minimum tej funkcji

reguła ta jest stosowana, gdy prognoza jest podstawą decyzji związany z dużymi nakładami finansowymi

PROGNOZOWANIE SZEREGÓW CZASOWYCH NA PODSTAWIE MODELU TRENDU

prognoza

Przeszłość najdalsza teraźniejszość

Horyzont prognozy

y ₁, .......,. y _{n model} y^*_n+1, …., y^*_T

_{przyszłość}

REGUŁA PROGNOZOWANIA

W modelach tych czas lub (i) przyszłe wartości zmiennej prognozowanej reprezentują wszystkie czynniki wpływające na zmienne. Metody te są stosowane, gdy zjawisko charakteryzuje się dużą inercją. Prognosta korzysta z zasady status quo(nie zmieniają się oddziaływania czynników)

Metody prognozowania przyczynowo-skutkowego

Model wyjaśnia mechanizm zmian zmiennych endogenicznych będących zarazem zmiennymi prognozowanymi, przez zmiany zmiennych objaśniających, którymi w przypadku modeli wielorównianiowych mogą być zmienne zarówno endogeniczne jak i egzogeniczne.

Parametry tych modeli szacuje się, korzystając z wielowymiarowych szeregów czasowych lub przekrojowo czasowych.

y₁, ............y_n x₁₁, ……., x_1n przeszłość model

x₂₁, ........., x_2n

.......................

x_m1, ..........., x_mn

y^*_n+1, ........., y^*_T x^*_1,n+1, ........., x^*_1,T

przyszłość reguła

prognozowania x^*_2,n+1, .........., x^*_2,T

..............................

x^*_m,n+1, ............, x^*_m,T

METODY ANALOGOWE:

Służą do przewidywania przyszłości danej zmiennej na podstawie danych o zmiennych podobnych, co do których istnieją zbyt słabe podstawy, by przypuszczać, że są one powiązane przyczynowo ze zmienną prognozowaną.

Metody heurystyczne

Metody te polegają na wykorzystaniu opinii ekspertów. Ekspert buduje model myślowy prognozowanego zjawiska uwzględniają fakty zarówno znane jak i przeczuwane właściwości ilościowe i jakościowe.

Reguła prognozowania

W praktyce często wykorzystywane są kombinacje różnych metod np. w różnych fazach konstruowania prognozy. Przykładem takiego postępowania jest metoda scenariuszy - specyficzna kombinacja metod przy zachowaniu pewnych zasad dochodzenia do scenariuszy.

Błąd prognozy: różnica

Q_t = y_t - y^*_t t>n,

gdzie:

y_t - zmienna prognozowana Y w czasie t>n

y^*_t - prognoza zmiannej Y na czas t>n

n- liczba obserwacji szeregu czasowego

Błąd prognozy ex post i ocena ex ante błędu (ocena wstępna wielkości błędu zamin nastapi czas realizacji błędu)

Błąd prognozy:

Q_t = y_t - y^*_t t>n,

gdzie:

y_t - zmienna prognozowana Y w czasie t>n

y^*_t - prognoza zmiannej Y na czas t>n

n- liczba obserwacji szeregu czasowego

Błąd ten może być określony po upływie czasu na który prognoza była ustalona - błąd ex post (trafność prognozy) lub przed upływem tego czasu - błąd ex ante (dokładność prognozy). Jest on szacowny w czasie wyznaczania prognozy i służy określeniu dopuszczalności prognozy.

TRAFNOŚĆ PROGNOZY

Stopień trafności prognozy ilościowej mierzy się za pomocą błędów ex post. Błędy te można obliczać dla pojedynczego momentu lub okresu t>n, dla każdego momentu lub okresu należącego do przedziału czasu (n+1, ......, T) zwanego przedziałem empirycznej weryfikacji prognozy.

Bezwzględny błąd prognozy ex post w czasie t:

q_t = y_t - y^*_t, t>n

Wartość błędu informuje, jak wielkie było w chwili t>n, odchylenie prognozy od wartości rzeczywistej zmiennej Y.

Względny błąd prognozy ex post w czasie t:

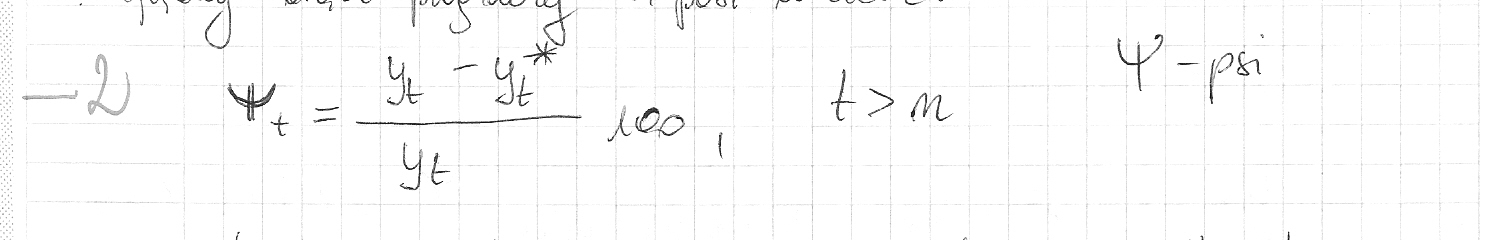
Wartość błędu informuje, jak wielkie było w chwili t>n odchylenie prognozy od wartości rzeczywistej zmiennej Y, liczone w procentach wartości rzeczywistej. Błąd ten może być obliczany tylko dla zmiennych mierzonych w skali ilorazowej.

Średni kwadratowy błąd prognozy ex post w przedziale weryfikacji:

Wartość S* informuje o przeciętnym odchyleniu prognoz od wartości rzeczywistych w przedziale empirycznej weryfikacji prognoz. Otrzymana wartość jest porównywalna z odchyleniami standardowymi reszt. Wektor prognoz moąna uznać za zadowalający, gdy:

S* ≤ S

Średni względny błąd prognozy ex post w przedziale weryfikacji:

wartość błędu informuje, jaki procent rzeczywistej wartości zmiennej Y stanowiło przeciętne w przedziale weryfikacji bezwzględne odchylenie prognoz od danych rzeczywistych.

Współczynnik THEILA dla przedziału weryfikacji prognoz:

Miernik ten przyjmuje wartość równą zeru, gdy prognozy są idealnie trafne. Im większa wartość miernika, tym większe są różnice między prognozą a rzeczywistą wartością zmiennej.

DOPUSZCZALNOŚĆ PROGNOZY

Prognoza jest dopuszczalna, gdy jest obdarzona przez jej odbiorcę takim stopniem zaufania, by mogłaby być wykorzystana w celu w jakim została ustalona.

Dopuszczalność prognozy jest określana w tym samym czasie w którym wyznacza się prognozę.

Maksymalny horyzont prognozy jest to należący do przyszłości najdalszy moment lub okres, w którym prognoza jest dopuszczalna.

Sposoby określenia dopuszczalności prognoz:

1/ błąd prognozy ex ante - może być tylko szacowany. Charakterystyką rozproszenia możliwych prognoz wokół możliwych realizacji zmiennej prognozowanej w czasie t>n jest wariancja prognozy.

V²_t = E(Y_t - y^*_t)², t>n

Pierwiastek kwadratowy z wariancji prognozy nosi nazwę bezwzględnego błędu prognozy ex ante.

Wartość błędu informuje o oczekiwaniach przeciętnych odchyleniach realizacji zmiennej prognozowanej od prognoz w czasie t>n.

Błąd ten służy określeniu dokładności prognozy. Prognoza jest tym dokładniejsza im mniejsza jest wartość v_t.

Dla modelu TRENDU LINIOWEGO oszacowanie wariancji prognozy przybiera postać:

T - numer okresu lub momentu dla którego wyznacza się prognozę

- średnia wartość zmiennej czasowej w szeregu o n obserwacjach

s- odchylenie standardowe reszt

Do porównania dokładności prognoz różnych zmiennych można wykorzystać względny błąd prognoz ex ante:

η - ni

Oba błędy - bezwzględny i względny - są obliczane dla pojedynczego momentu lub okresu t>n.

Gdy prognoza jest określona na przedział czasu [n+1, ..... T], błędy oblicza się dla każdego t.

Prawdopodobieństwo realizacji prognozy jest drugim sposobem określania dopuszczalności prognozy.

Jeżeli zmienna prognozowana jest zmienną losową skokową to należy wyznaczyć:

P(Y_t = y^*_t) = γ_t, t>n

Gdzie:

γ - jest prawdopodobieństwem, że zmienna Y przyjmie w czasie t>n wartośc y_t

P - prawdopodobieństwo realizacji

γ - gamma

Jeżeli zaś zmienna prognozowana jest zmienną losową ciągłą to:

P( Y_t - y^*_t < ∑ ) = γ_t, t>n

Gdzie:

∑ - jest dowolnie małą, dodatnią liczbą otrzymaną np. jako krotność błędu ex ante.

γ_t - nosi nazwę wiarygodności prognozy

Uznajemy za dopuszczalną taką prognozę, dla której:

gdzie:

jest wartością progową (bliską jedności) prawdopodobieństwa realizacji prognozy określoną przez odbiorcę.

III wykład

PROGNOZOWANIE NA PODSTAWIE SZEREGÓW CZASOWYCH

Składowe szeregu czasowego

W klasycznym opisie szeregu czasowego wyróżnia się 4 składowe:

• trend (T)

• wahania rytmiczne (S)

• wahania cykliczne ©

• wahania nieregularne (przypadkowe) (E)

TREND (T) - reprezentuje trwałą, zwyżkową lub zniżkową tendencję rozwojową. Wyraża zmiany rozmiarów danego zjawiska w czasie. Jest efektem działania przyczyn głównych, które powodują że mimo występowania przyczyn ubocznych dane zjawisko rozwija się w określonym kierunku

WAHANIA RYTMICZNE (S) - to w miarę regularne wahania, zarówno ze względu na czas trwania fazy jak i amplitudę. Mogą to być: wahania krótkookresowe (w ciągu dnia, doby, tygodnia, miesiąca) oraz wahania sezonowe, czyli takie zmiany których cykl realizuję się w ciagu roku np. dane z turystyki, rolnictwa

WAHANIA CYKLICZNE (.C) - są to falowe zmiany badanego zjawiska wokół trendu obserwowalne w stosunkowo długich przedziałach czasu. W działalności gospodarczej są one nazywane wahaniami koniunkturalnymi (np. podaż, popyt towarów i usług, stopa bezrobocia, obroty na giełdzie papierów wartościowych) są trudne do przewidywania ze względu na zmieniającą się długość fazy i amplitudę

WAHANIA NIEREGULARNE (E) - są składową występującą we wszystkich szeregach i wynikają z działania przyczyn ubocznych

Model rozwoju danego zjawiska w czasie zawierającego wymierzone składowe może być:

• 
  modelem addytywnym o postaci :

Y = T + S + C + E

- lub modelem multiplikatywnym

Y = T x S x C x E

METODY NAIWNE

Metody te są oparte na przesłance, że nie następują zmiany w dotychczasowym sposobie oddziaływania czynników określających wartości zmiennej prognozowanej w wyniku czego np. sprzedaż wyrobów w następnym kwartale będzie kształtować się na dotychczasowym poziomie. Umożliwiają one konstrukcję prognoz krótkookresowych na jeden okres na przód.

Najczęściej przyjmowany model konstrukcji prognozy na moment lub okres „t” ma postać:

y^*_t = y_t - 1

gdzie: y^*_t - prognoza zmiennej Y

y_t-1 wartość zmiennej prognozowanej w momencie lub okresie t-1

Do oceny dopuszczalności prognozy można użyć np. średniego kwadratowego błędu ex post prognoz wygasłych.

W modelu addytywnym:

W wybranej jednostce czasu różnice między wybraną tendencją a rzeczywistą wartością zmiennej w przybliżeniu stanowi taką samą wartość.

W modelu multiplikatywnym - tendencja wzrostowa amplituda zmian się zwiększa

METODA ŚREDNIEJ RUCHOMEJ (średnia arytmetyczna)

Modele średniej ruchomej (łańcuchowej) mogą być wykorzystywane zarówno do wygładzenia szeregu czasowego, jak i do prognozowania. Zastosowanie średniej ruchomej powoduje „wygładzenie” szeregu czasowego, które eliminuje wahania przypadkowe i (lub) wahania sezonowe, a także cykliczne o ile one występują.

Wyznaczenie trendu tą metodą polega na obliczeniu z pierwszych „m” wyrazów szeregu średniej arytmetycznej. Następnie obliczamy drugą średnią arytmetyczną z „m” wyrazów opuszczając pierwszy wyraz szeregu czasowego i równocześnie uwzględniając m+1-szy. I tak, kolejno obliczamy średnie arytmetyczne z „m” wyrazów, przesuwając wskaźnik o jednostkę, aż do wyczerpania wartości.

Działania te można zapisać wzorem:

y_i + y_n+1 + ...... + y_i+m-1

y_i =

m

Dla m=5 średnią ruchomą obliczamy następująco:

y₁ + y₂ + y₃ + y₃ + y₅

y₁ =

5

Y₂ + y₃ + y₄ + y₅ + y₆

y₂ =

5

itd....

gdy „m” jest liczbą nieparzystą wartość średniej ruchomej zostają przyporządkowane okresowi środkowemu spośród „m” wyrazów.

Jeżeli „m” jest parzyste to należy wykonać tzw. Centrowanie średniej ruchomej, które polega na obliczeniu średniej arytmetycznej z dwóch sąsiadujących wartości y_t, y_{t+1i przypisaniu jej środkowej} wartości.

Używając modeli średniej ruchomej do prognozowania, przyjmuje się że wartość zmiennej prognozowanej w następnym momencie lub okresie będzie równe średniej arytmetycznej z ostatniej wartości tej zmiennej.

Model średniej ruchomej prostej:

1 t-1

Y^*_t = ∑ y_i

K i=t-k

Gdzie:

Y^*_t - prognoza zmiennej Y wyznaczona na moment lub okres t

Y_i - wartość zmiennej prognozowanej

K - stała wygładzania (liczna wyrazów średniej ruchomej)

Do wyznaczania liczby wyrazów średniej ruchomej można użyć błędów prognoz ex post np. średniego kwadratowego błędu prognozy ex post z którego wartośc pierwiastka wyraża odchylenie prognoz wygasłych od wartości zmiennej prognozowanej

1 n

S^*2 = ∑ (y_t - y^*_t)²

n-k t=k+1

Spośród możliwych wartości stałej k, wybiera się tę liczbę dla której wielkość błędu jest najmniejsza.

PROSTY MODEL WYGŁADZANIA WYKŁADNICZEGO

Model ten może być stosowany w przypadku występowania w szeregu czasowym, prawie stałego poziomu zmiennej prognozowanej oraz wahań przypadkowych. Punktem wyjścia do opisu modelu jest równanie modelu średniej ruchomej prostej.

Analizowany model zapisujemy:

Y^*_t = F_t-1 = y^*_t-1 + ∝q_t-1

Parametr wygładzania ∝ jest liczbą z przedziału (0,1). Jeżeli ma wartość bliską jedności, to budowana prognoza będzie uwzględniała w wysokim stopniu błędy ex post prognoz. Wartość parametru wygładzania wyznacza się z reguły eksperymentalnie konstruując na podstawie próbki wstępnej prognozy dla różnych wartości ∝.

Konstrukcja prognozy metodą średniej ruchomej prostej:

t	Sprzedaż Yt	Prognoza Yt^*	Błąd Qt = yt- y^*t	Qt^2
1	54	-	-	-
2	52	-	-	-
3	64	-	-	-
4	48	(54+52+64)/3=56,7	-8,7	75,7
5	66	(52+64+48)/3=54,7	11,3	127,7
6	64	(64+48+66)/3=59,3	4,7	22,10
7	68	(48+66+64)/3=59,3	8,7	75,7
8	58	(66+64+68)/3=66,0	-8	64
9	64	(64+68+58)/3=63,3	0,7	0,5
10	68	(68+58+64)/3=63,3	4,7	22,1
11	52	(58+64+68)/3=63,3	-11,3	127,7
12	56	(68+52+56)/3=

548,6

S^* = = 7,8 tys szt

9

Konstrukcja prognozy metodą wygładzania wykładniczego (∝ = 0,2)

t	Sprzedaż	prognoza	błąd	Kw.błędu
1	54	56,7	-2,7	7,3
2	52	56,7+0,2(-2,7)= 56,2	-4,2	17,6
3	64	56,2+0,2(-4,2)=55,4	8,6	74,0
4	48	55,4+0,2(8,6)=57,10	-9,1	82,8
5	66	57,1+0,2(-9,1)=55,3	10,7	114,5
6	64	55,3+0,2(10,7)=57,4	6,6	43,6
7	68	57,4+0,2(6,6)=58,7	9,3	86,5
8	58	58,7+0,2(9,3)=60,6	-2,6	6,8
9	64	60,6+0,2(-2,6)=60,1	3,9	15,2
10	68	60,1+0,2(3,9)=60,9	7,1	50,4
11	52	60,9+0,2(7,1)=62,3	-10,3	106,1
12	56	62,3+0,2(-10,3)=60,2	-4,2	17,6
13	----	60,2+0,2(-4,2)=59,4	----------	------

622,4

622,4

S^* = = 7,2 tyś szt

12

LINIOWA FUNKCJA TRENDU

Funkcja trendu jest funkcją matematyczno-opisującą zmiany badanego zjawiska w czasie

∧

y = f(t)

Wyznaczenie trendu sprowadza się do opracowania wartości parametrów funkcji w której rolę zmiennej niezależnej (objaśniającej) pełni czas

Jeżeli przyjmiemy, że funkcja trendu f(t) jest funkcją liniową to możemy ją zapisać:

f(t) = a₀ + a₁t

Załóżmy że dysponujemy informacjami o zintegrowaniu się wartości y mamy więc ciąg par liczb uporządkowanych wg czasu

(t₁, y₁), (t₂, y₂), ...., (t₁, y_n);

t - zmienna czasowa przybierająca kolejne liczby naturalne t=1 dla okresu początkowego

Przy przyjętych oznaczeniach równanie liniowej funkcji trendu zapiszemy jako:

∧

y_t = a₀ + a₁t_i

W wyniku zastosowania metody najmniejszych kwadratów otrzymujemy układ równań normalnych

n n

∑ y_i = na₀ + a₁ ∑ t_i

i=1 i=1

n n n

∑ y_it_i = a₀ ∑ t_i + a₁ ∑ t_i²

i=1 i=1 i=1

METODY WYZNACZNIKÓW:

n ∑ ti

W = = n ∑ t _i² - ∑ _t ∑ _ti = 16 x 1496 - 136 x 136 = 5440

∑ ti ∑ t²_i

∑ yi ∑ ti

Wa₀ = = 479,5 x 1496 - 5309,7 x 136 = - 0,88

∑ yiti ∑ t²_i

n ∑ yi

Wa₁ = = 16 x 5309,7 - 136 x 479,5 = 3,63

∑ ti ∑ yiti

Wa₀ Wa₁

a ₀ = ; a₁ =

W W

Przykład:

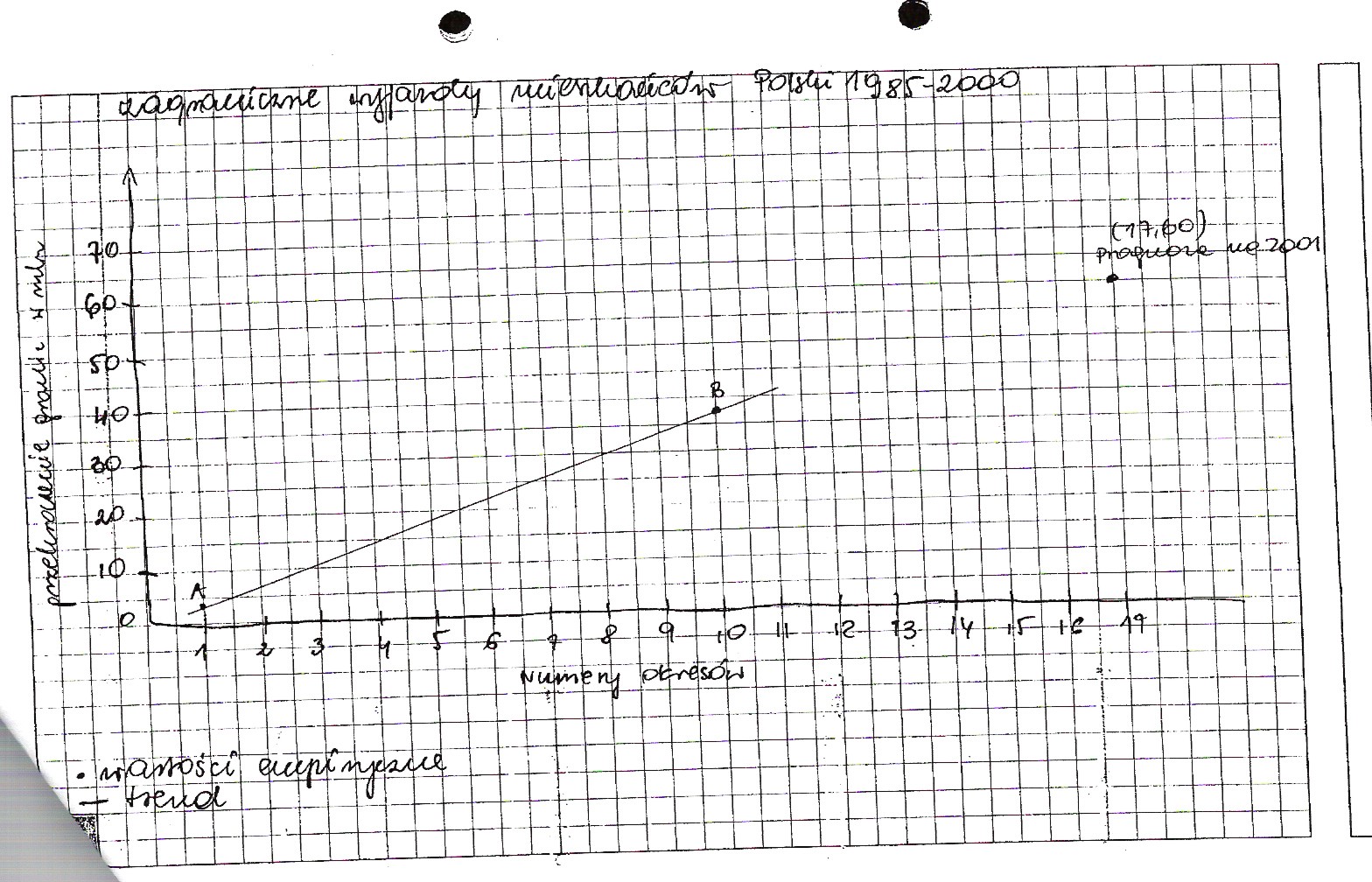
Zagraniczne wyjazdy mieszkańców Polski w latach 1985-2000 (w mln wyjazdów)

• oszacować parametry funkcji trendu

• obliczyć miary dobroci dopasowania funkcji

• ustalić prognozę na rok 2001

• obliczyć bezwzględny i względny błąd prognozy ex ante.

(tabela w załączniku w exelu)

n ∑ ti 16 136

W = = = 16x1496 - 136X136= 23936-18496=54,40

∑ ti ∑ t²_i 136 1496

∑ yi ∑ ti 479,5 136

Wa_o = = = 479,5x 1496 - 5309,7 x 136 = - 0,88

∑ yiti ∑ t²_i 5309,7 1496

n ∑ yi 16 479,5

W _a1 = = = 16 x 5309,7 - 136 x 479,5 = 3,63

∑ ti ∑ yiti 136 5309,7

W wyniku przeprowadzonych obliczeń otrzymujemy równanie trendu:

∧

y_i = -0,88 + 3,6293 t_i

W ciągu 16 lat (1985-2000) liczba zagranicznych wyjazdów mieszkańców Polski zwiększyła się corocznie przeciętnie o 3,63 mln wyjazdów.

S_ε = 2,16 (y² = 0,0165)

∧

A ( 1; 2,75) y₁ = -0,88+3,63X1 = 2,75

∧

B ( 10; 35,42) y₁₀ = -0,88+3,63x10 = 36,3-0,88 = 35,42

------

W_a1 W_a1

a₀ = ; a₁ =

W W

Powtórka ostatniego wykładu

Przy przyjętych oznaczeniach równanie liniowej funkcji trendu zapiszemy jako:

∧

y_i = a₀ + a₁t (parametry funkcji)

w wyniku zastosowania metody najmniejszych kwadratów otrzymujemy układ równań nominalnych:

n n

∑ y_i = na₀ + a₁ ∑ t_i ,

i=1 i=1

n n n

∑ y_it_i = a₀ ∑ t_i + a₁ ∑ t²_i,

i=1 i=1 i=1

Przykład:

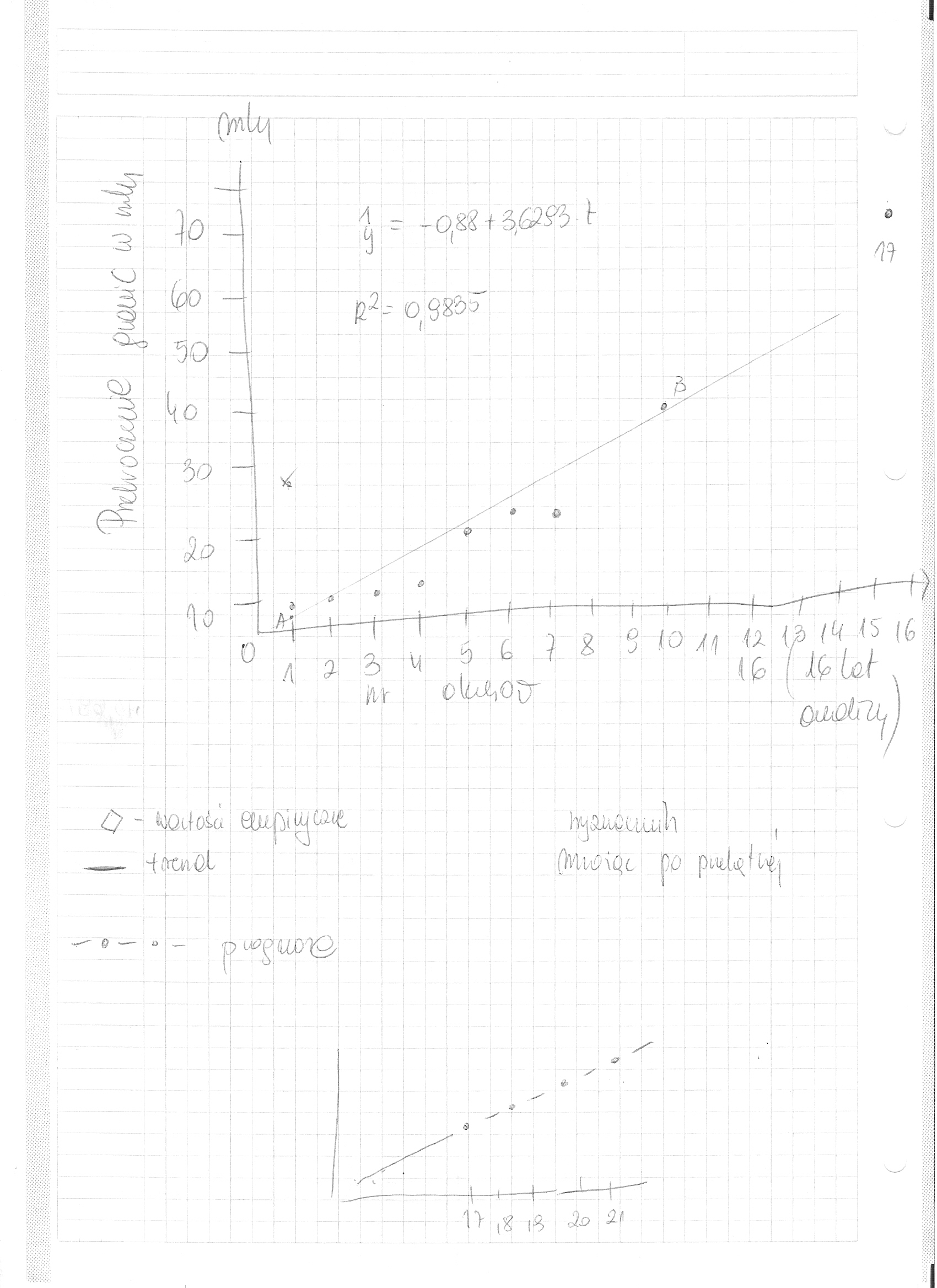
Zagraniczne wyjazdy mieszkańców Polski w latach 1985-2000 w mln wyjazdów

• oszacować parametry funkcji trendu

• obliczyć miary dobroci dopasowania funkcji

• ustalić prognozę na rok 2001

• obliczyć bezwzględny i względny błąd prognozy ex ante

W wyniku przeprowadzonych obliczeń otrzymujemy równanie trendu:

∧

y_i = -0,88 + 3,6293 t_i

W ciągu 16 lat (1985-2000) liczba zagranicznych wyjazdów mieszkańców Polski zwiększyła się corocznie przeciętnie o 3,63 mln wyjazdów

S _ε = 2,16 (ϕ ² = 0,0165)

∧

y_i = -0,88 + 3,6293 t_i

∧

A ( 1; 2,75) y₁ = -,0,88 +3,63x1 = 2,75

B (10; 35,42) ∧

y₁₀ = -,0,88 +3,63x10 = 36,30-0,88 = 35,42

,

Opinia ekspertów o

Prognozowanym zjawisku

prognoza

Zastosowanie: wg analizy wykresu żeby wiedzieć czy to czy to

---