1. Zbiory i działania na nich (przykłady): pojęcia pierwotne: •
- a jest elementem zbioru A
•
- A jest zawarty w B
•
- A jest podzbiorem B
• A = B - zbiory pokrywają się
•
- zbiór A jest podzbiorem właściwym zbioru B
Przykłady: N - naturalne, Q - wymierne, R - rzeczywiste, {a₁…….a_n} - zbiór skończony o n elementach, {x: P(x)} zachodzi warunek P(x).
• Zbiór pusty: ø zbiór do którego nie należy żaden element, np. x²+1=0
Działania na zbiorach:
• suma
wszystkie i tylko te elementy, które należą do A i B, np.

• iloczyn (przekrój)
(wszystkie, które należą do A i B)
• różnica A \ B (wszystkie, które należą do A ale nie należą do B
2. Prawa rachunku zbiorów:
• przemienność dodawania

• przemienność przekroju

• łączność dodawania

• łączność przekroju

• rozdzielność przekroju względem dodawania

• rozdzielność dodawania względem przekroju

3. Produkty kartezjańskie i relacje:
X i Y: produktem kartezjańskim tych zbiorów nazywamy zbiór wszystkich uporządkowanych par (x,y), gdzie
.

- produkt kartezjański. Przykłady: zbiór punktów płaszczyzny jest produktem kartezjańskim R x R.
Dany jest X x Y, wtedy relacja nazywamy każdy podzbiór tego produktu.
(x pozostaje w relacji ρ z y). Przykład: X i Y należą do R, wykres y=x² będzie zbiorem par (x,x²) będzie to relacja.
Rodzaje relacji:
• relacja zwrotna -
,
mamy x ρx, np. relacja równości w zbiorze X, x=X, x=X
• relacja symetryczna
, gdy z warunku xρy wynika yρx, np. relacja równoległości prostych na płaszczyźnie
• relacja przechodnia
, gdy xρy i yρx implikują warunek xρz, np. relacja nie większości

• relacja równoważności -
, jest ona równocześnie zwrotna, symetryczna i przechodnia
• relacja antysymetryczna
, gdy z xρy i yρx wynika x=y, np. relacja nie większości

• relacja spójna
, dla każdych dwóch różnych elementów x i y zbioru X albo xρy i yρx, np. relacja niewiekszości.
def. Relacja, która jest jednocześnie przechodnia, antysymetryczna i spójna nazywa się relacją liniowo porządkującą zbiór X.
4. Zbiór liczb rzeczywistych. Własności. Kresy górny i dolny:
pojęcia pierwotne: zbiór R, relacja niewiększości, działania dodawania i mnożenia.
Aksjomaty dotyczące R:
• x+y=y+x przemienność
• (x+y)+z=x+(y+z) łączność
• istnieje taki element 0 należący do R, taki że x+0=x
• istnieje taki element -x, taki że x+(-x)=0 jest to tzw. Przeciwny znak
Def. Zbiór X nal. do R nazywa się ograniczonym z góry, gdy istnieje taki element spełniający powyższy warunek, mówimy, że ogranicza zbiór X z góry.
Def. Najmniejszy z elementów ograniczających zbiór X z góry nazywamy kresem górnym tego zbioru. K nal. do R nazywa się kresem górnym dla X gdy dla każdego x należącego do X mamy x≤k oraz dla każdego M<k istnieje element x nal. do X taki, że x>M. kres górny oznaczamy symbolem supX (supremum - największy).
Def. Zbiór X nal. do R nazywamy ograniczonym z dołu, gdy istnieje m takie, że dla każdego x nal. do X X≥m
Def. Zbiór, który jest ograniczony z góry i z dołu nazywamy ograniczonym.
Def. Największy z elementów ograniczających zbiór X z dołu nazywa się kresem dolnym i oznaczamy go symbolem inf X można udowodnić, że każdy niepusty i ograniczony z dołu podzbiór zbioru R ma kres dolny.
5. Kwantyfikatory:
Def. Zapis, w którym występują litery x,y,z oznaczające dowolne liczby, a które po podstawieniu za te litery dowolnej liczby stają się albo zdaniem prawdziwym albo zdaniem fałszywym. Niech P(x) oznacza pełną funkcję zdaniową, wówczas zapis
oznacza zbiór tych wszystkich liczb x należących do zbioru X dla których funkcja zdaniowa P(x) jest prawdziwa. Przy zapisie funkcji zdaniowych używamy często symboli zwanych kwantyfikatorami. P(x) i Q(x) są niektórymi funkcjami zdaniowymi
•
dla każdego x jest P(x)
•
istnieje takie x, że zachodzi P(x)

kwantyfikator ogólny

kwantyfikator szczegółowy
Niech P oznacza zdanie orzekające (prawdziwe lub fałszywe) wówczas za jego pomocą możemy utworzyć zdanie zaprzeczające
nieprawda, że P. Ważne są reguły postępowania z zaprzeczeniami zdań, w których występują kwantyfikatory.

6. Ciąg liczbowy. Ograniczony. Monotoniczny:
ciągiem liczbowym nazywamy funkcję odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych. Wartości tej funkcji dla liczby naturalnej n nazywamy n-tym wyrazem i oznaczamy a_n lub b_n, ciągi o takich wyrazach oznaczamy odpowiednio przez (a_n) (b_n). obrazowo ciąg można traktować jako zbiór ponumerowanych liczb, które są poustawiane według rosnących numerów.
Def. Ciąg a_n jest ograniczony z góry jeżeli zbiór liczb
jest ograniczony z góry tzn. jeżeli

Def. Ciąg a_n jest ograniczony z dołu jeżeli zbiór liczb
jest ograniczony z dołu, tzn.

Def. Ciąg a_n jest ograniczony
jest ograniczony i z dołu i z góry.
Def. Ciąg a_n jest rosnący jeżeli a₁<a₂<a₃<…, tzn.
obrazowo można powiedzieć, że ciąg jest rosnący, gdy jego wyrazy powiększają się ze wzrostem indeksu, np.

Def. Ciąg a_n jest niemalejący
a₁≤a₂≤a₃≤… albo

Analogicznie jest dla ciągów malejących i nierosnących.
Monotoniczność ciągu a_n możemy ustalić badając znak różnicy a_n+1-a_n a ciąu b_n wyrazach (+) porównując
z jedynką.

an+1-an	bn+1/bn	ciąg
> 0 ≥ 0 < 0 ≤ 0	> 1 ≥ 1 < 1 ≤ 1	rosnący niemalejący malejący nierosnący

7. Ciąg zbieżny. Ciąg rozbieżny:
Def. Ciąg (a_n) jest zbieżny do liczby a
zachodzi: |a_n-a|<ε obrazowo można powiedzieć, że ciąg jest zbieżny do liczby a gdy jego dostatecznie dalekie wyrazy dążą dowolnie blisko od liczby a.
Def. (granicy nieskończonej)
Ciąg (a_n) jest zbieżny do granicy nieskończonej
zachodzi:
|a_n|> ε obrazowo możemy powiedzieć, że ciąg jest zbieżny do granicy nieskończonej gdy dostatecznie dalekie moduły wyrazów tego ciągu są większe od dowolnie dużej liczby.
• ciąg a_n jest zbieżny do +∞
zachodzi a_n>ε
• ciąg a_n jest zbieżny do -∞
zachodzi a_n<ε
ciągi które nie maja granicy skończonej albo nieskończonej nazywamy ciągami rozbieżnymi.
Tw. (warunek Cauchy'ego zbieżności ciagu)
ciąg a_n jest zbieżny
zachodzi |a_n-a_m|< ε
8. Podciągi. Twierdzenie Bolzano - Weierstrassa:
Def. Niech a_n będzie dowolnym ciągiem, oraz niech (n_k) będzie rosnącym ciągiem liczb naturalnych. Podciągiem ciągu a_n nazywamy ciąg b_k określony wzorem
. Możemy powiedzieć, że podciągiem nazywamy ciąg pozostały po skreśleniu niektórych liczb i wyrazów tego ciągu, np. ciąg liczb parzystych jest podciągiem liczb naturalnych.
Tw. (Bolzano - Weierstrassa)
każdy ograniczony ciąg ma zbieżny podciąg. Nieograniczony ciąg ma podciąg zbieżny do +∞ lub -∞ .
9. Arytmetyka granic ciągów:
• zbieżny ciąg jest ograniczony (uwaga! Nie każdy ograniczony ciąg jest zbieżny)
• ciąg a_n→0 gdy |a_n|→0
• o arytmetyce ciągu: a_n→a i b_n→b to:
- a_n
b_n → a
b
- a_n ∙b_n → a ∙ b
-

-

-

10. Twierdzenie o 3 ciągach i o ciągu monotonicznym:
Tw. (o 3 ciagach)
niech ciągi (a_n), (b_n) i (c_n) spełniają warunki a_n≤b_n≤c_n i niech a_n→a, c_n→a, wówczas b_n→a
Tw. (o ciągu monotonicznym ograniczonym)
jeżeli (a_n) jest niemalejący n>n₀ i ograniczony z góry to jest zbieżny do granicy sup{a_n:n≥n₀}.
prawdziwe jest także analogiczne stwierdzenie dla ciągu nierosnącego i ograniczonego z dołu.

11. Twierdzenie o granicach nieskończonych:
Tw. (o 2 ciągach)
niech ciąg a_n≤b_n dla każdego n>n₀ i niech a_n→+∞ wtedy b_n→+∞. Podobnie dla ciągów zbieżnych do -∞.
Tw. (o arytmetyce granic nieskończonych)

• +∞ + a = +∞ dla -∞<a≤+∞ • dla -∞<a<+∞ • dla 0≤a<1 • dla -∞≤b<0

• a(+∞)=+∞ dla 0<a≤+∞ • dla 0<a≤+∞ • dla 1<a≤+∞ • dla 0<b<+∞

Symbole nieoznaczone:


12. Granice specjalne qⁿ, eⁿ,
:



•

•

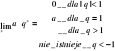
13. Podstawowe określenia funkcji, dziedzina, wykres:
Def. Funkcją określoną na zbiorze X zawierającym się w R o wartościach w zbiorze Y zawierającym się w R nazywamy przyporządkowanie x należące do X dokładnie jednego elementu y należącego do Y. funkcję tą oznaczamy f: X→Y
Zbiór X nazywamy dziedziną funkcji f
Zbiór Y nazywamy przeciwdziedziną.
Zbiór tych liczb {f(x)nal. do Y: x nal. X} nazywamy zbiorem wartości funkcji f.
Wykresem funkcji f nazywamy zbiór {(x,y): x nal. X, a y=f(x)}
14. Klasy funkcji, okresowa, parzysta, ograniczona, monotoniczna:
• funkcje okresowe:
funkcje f: X→R nazywamy okresową jeżeli istnieje T>0 takie ze
oraz f(x+T)=f(x)
liczbę T nazywamy okresem funkcji
np. y=sin x, sin (x+2π)=sin x T=2π
• funkcje parzyste
f: X→R gdy

• funkcje nieparzyste
f: X→R gdy

• funkcje ograniczone z góry (z dołu)
f: X→R gdy zbiór jej wartości na tym zbiorze jest ograniczony z góry (z dołu) tzn.

funkcję ograniczona z góry i z dołu nazywamy ograniczoną.
• funkcje rosnące (malejące), niemalejące (nierosnące)
gdy
zachodzi nierówność f(x₁)<f(x₂) i odpowiednio: f(x₁)> f(x₂); f(x₁)≤ f(x₂); f(x₁)≥ f(x₂)
15. Funkcja odwrotna:
Def. Niech funkcja f: X→Y będzie różnowartościowa, funkcja odwrotną do funkcji f nazywamy funkcję f^-1 z dziedziną równa zbiorowi wartości funkcji f i przeciwdziedziną X, która jest określona przez warunek:

wykres funkcji odwrotnej otrzymujemy z wykresu funkcji f odbijając go symetrycznie względem prostej y=x.
Własności:
• f^-1(f(x))=x
• f(f^-1(y))=y
np. arcsin x, arccos x, arctg x, arcctg x
16. Funkcje elementarne i nieelementarne:
podstawowymi funkcjami elementarnymi nazywamy funkcje stałe, potęgowe, wykładnicze, logarytmiczne, trygonometryczne oraz cyklometryczne. Funkcje, które można otrzymać z podstawienia funkcji za pomocą skończonej liczby działań elementarnych oraz operacji złożenia funkcji nazywamy funkcjami elementarnymi. Np. •

• wielomian

• funkcje wymierne, tzn. funkcje które można zapisać w postaci ilorazu 2 wielomianów


• funkcje hiperboliczne: sh x, ch x, th x, ctg x
Funkcje nie elementarne:
• signum


• funkcja Dirichleta

17. Sąsiedztwo. Definicja Heinego granicy funkcji:
Def. Sąsiedztwem (lewostronnym, prawostronnym) o promieniu r>0 punktu
nazywamy zbiór
jeżeli promień r sąsiedztwa nie będzie istotny w naszych rozważaniach, to będziemy mówili prosto o sąsiedztwie S(x₀), S(x₀⁺), S(x₀^-)
Def. (Heinego funkcji w punkcie)
Niech funkcja f będzie oznaczona przynajmniej na sąsiedztwie S(x₀) liczba a jest granicą funkcji f w punkcie x₀ gdy dla każdego ciągu x_n→ a:
zachodzi: f(x_n)→ a


18. Definicja Cauchy'ego. Granica lewostronna i prawostronna:
Def. (granicy funkcji w punkcie Cauchy'ego)
niech funkcja f będzie określona przynajmniej na sąsiedztwie punktu x. Liczba a jest granicą funkcji w punkcie x₀ gdy
, że z nierówności
Def. (granicy lewostronnej)
niech funkcja f jest określona przynajmniej na sąsiedztwie S(x₀^-). Liczbę a nazywamy granicę lewostronną funkcji f w punkcie x₀ gdy
zachodzi f(x_n)→ a


w podobny sposób określa się granice prawostronną.
19. Granice nieskończone i granice w nieskończoności:
Def. niech funkcja f będzie określona na sąsiedztwie S(x₀) i ma granicę +∞ w punkcie x₀ gdy dla każdego x_n→x₀ i x_n nal. do S(x₀) zachodzi f(x_n)→ +∞

Def. Sąsiedztwem -∞ nazywamy przedział
S(-∞)=(-∞,a),
Sąsiedztwem +∞ nazywamy przedział S(+∞)=(b,+ ∞)
Def. Niech funkcja f będzie określona przynajmniej na sąsiedztwie S(+∞). Liczba a jest granica funkcji f w +∞ gdy dla każdego x_n→+∞ zachodzi f(x_n)→a


20. Arytmetyka granic funkcji:
Jeżeli funkcje f i g maja skończone granice a i b w punkcie x₀ to dla x→x₀ zachodzi:
•

• f(x) ∙ g(x) → a ∙ b
• c ∙ f(x) → c∙a, c nal. do R
•
o ile b≠0
•
o ile a≠0 i b≠0
21. Arytmetyka granic nieskończonych:

• +∞ + p = +∞ dla -∞<p≤+∞ • dla -∞<p<+∞ • dla 0^+≤p<1 • dla -∞≤q<0

• p(+∞)=+∞ dla -0<p≤+∞ • dla -0<p≤+∞ • dla 1<p≤+∞ • dla 0<q<+∞

22. Granice podstawowych wyrażeń nieoznaczonych: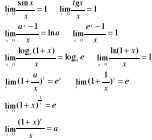


23. Otoczenie. Definicja ciągłości:
Def. Otoczeniem (lewostronnym, prawostronnym) o promieniu r>0 punktu x₀ nal. do R nazywamy zbiór

O(x₀)
Def. Niech funkcja f będzie określona przynajmniej na otoczeniu O(x₀) punktu x₀. funkcja f jest ciągła w tym punkcie, gdy granica
istnieje. Obrazowo - gdy wykres funkcji nie przerywa się w punkcie x₀
24. Ciągłość jednostronna. Ciągłość na przedziale:
Def. Niech funkcja f będzie określona przynajmniej na otoczeniu O(x₀^-) punktu x₀. Jest lewostronnie ciągła w x₀ gdy

podobnie dla prawostronnie ciągłej
Def. Funkcja f jest ciągła na przedziale otwartym, gdy jest ciągła w każdym punkcie tego przedziału. Funkcja jest ciągła na przedziale domkniętym [a,b], gdy jest ciągła w każdym pkt. przedziału otwartego (a,b) oraz prawostronnie ciągła w pkt. a i lewostronnie ciągła w pkt. b.

25. Rodzaje nieciągłości:
mówimy, że funkcja f określona na otoczeniu pkt. x₀ jest nieciągła w tym punkcie, gdy granica
lub nieistineje.
def. funkcja f ma w pkt. x₀ nieciągłość 1 rodzaju jeżeli istnieją granice skończone
oraz

rozróżniamy dwa podrodzaje:
• funkcja f ma w pkt. x₀ nieciągłość 1 rodzaju typu „skok” gdy

• jeżeli funkcja f spełnia warunek
, to mówimy że funkcja f ma w punkcie x₀ nieciągłość 1 rodzaju typu „luka”.
np.
1. f(x) =
ma w punkcie 0 nieciągłość 1 rodzaju typu „skok”.
def. Funkcja f ma w pkt. x₀ nieciągłość 2 rodzaju jeżeli przynajmniej jedna z granic
nie istnieje lub jest nieskończona.
np. funkcja Dirichleta

ma nieciągłość 2 rodzaju w każdym punkcie x₀ należącym do R, ponieważ w każdym takim punkcie nie ma ona granicy lewostronnej ani prawostronnej.

26. Działania na funkcjach ciągłych:
Tw. (o arytmetyce ciągłości)
jeżeli funkcje f i g są ciągłe w pkt. x₀, to funkcja f+g, f-g, f∙g, f/g są ciągłe w tym punkcie x_0.
Tw. (o ciągłości funkcji złożonej)
jeżeli funkcja y=f(x) jest ciągła w punkcie x₀ a funkcja z=g(y) jest ciągła w pkt. y₀=f(x₀) wtedy funkcja złożona g○f jest ciągła w pkt. x₀. z=g(f(x))
Tw. (o ciągłości funkcji odwrotnej)
jeżeli funkcja f jest ciągła i rosnąca w przedziale [a,b], to funkcja odwrotna f^-1 jest ciągła i rosnąca w przedziale [f(a),f(b)]
Tw. (ciągłość funkcji elementarnej)
Funkcje elementarne są ciągłe w swoich dziedzinach.
27. Twierdzenie Weierstrassa o funkcji na przedziale domkniętym:
Tw. (Weierstrassa)
Jeżeli funkcja f jest ciągła na przedziale domkniętym i ograniczonym [a,b] to jest ona na nim ograniczona oraz osiąga swe kresy. Tzn. że istnieją takie liczby c i d należące do [a,b], że inf f(x)=f(c) i sup f(x)=f(d).
28. Twierdzenie Darboux o wartości pośredniej:
Tw. (Darboux)
Jeżeli funkcja f jest ciągła na przedziale [a,b] oraz f(a)<f(b), to dla każdego u należącego do (f(a),f(b)) istnieje c należący do (a,b) taka, że f(c)=u
29. Pochodne. Pochodne funkcji elementarnych:
Def. Niech x₀ należy do R, oraz niech funkcja f będzie określona przynajmniej na otoczeniu O(x₀). Pochodną funkcji f w punkcie x₀ nazywamy
i oznaczamy przez f'(x₀).
Niech Δx=x- x₀
wtedy mamy:
.
stosujemy także symbol

30. Interpretacja geometryczna pochodnej:
Def. Niech funkcja ciągła g będzie określona przynajmniej na otoczeniu O(x₀). Prosta jest styczna do wykresu funkcji f w pkt. x₀ jeżeli jest granicznym położeniem siecznych funkcji przechodzących przez pkt. (x₀,f(x₀)) i (x,f(x)), gdy x→x₀
f'(x₀)=tgα, gdzie α oznacza kąt między styczną do wykresu funkcji f i dodatnią częścią osi .
Równanie stycznej do wykresu funkcji f w pkt. (x₀,f(x₀))
y=f(x₀)+f'(x₀)(x-x₀)
31. Interpretacja fizyczna pochodnej:
Def. Niech S(t) oznacza położenie na osi punktu materialnego w chwili t. Wtedy szybkość pkt. w chwili t₀

32. Arytmetyka pochodnej:
Jeżeli funkcje f i g mają pochodne skończone w punkcie x₀ to:
•

•

•

•

33. Pochodna funkcji złożonej:
Tw. ( o pochodnej funkcji złożonej)
Jeżeli funkcja f ma pochodną skończoną w pkt. x₀, a funkcja g ma pochodna skończoną w f(x₀) to funkcja złożona g○f ma pochodną w pkt. x₀ ponadto (g○f)'(x₀)=g'(f(x₀)f'(x₀)
34. Pochodna funkcji odwrotnej:
Tw. Jeżeli funkcja f spełnia następujące warunki:
• jest ciągła na otoczeniu O(x₀)
• jest malejąca albo rosnąca na otoczeniu O(x₀)
• ma pochodną skończoną w pkt x₀ i ta pochodna nie równa się 0
wtedy funkcja odwrotna f^-1 ma pochodną w pkt. y₀=f(x₀), przy czym (f^-1)'(y₀)=1/f'(x₀)
35. Różniczka funkcja. Zastosowanie do obliczeń przybliżonych:
Tw. (różniczka)
niech funkcja f ma pochodną skończoną w pkt. x₀ jej różniczką w tym punkcie nazywamy funkcję df od zmiennej Δx=x-x₀ określoną wzorem:

Tw. (o zastosowaniu różniczki do obliczeń przybliżonych)
jeżeli funkcja f ma pochodna skończoną w pkt. x₀,
. Przybliżenie tzn., że błąd jaki popełniamy zastępując przyrost funkcji
Δf=f(x₀+Δx)-f(x₀) jej różniczką f'(x₀)Δx dąży szybciej do 0 niż przyrost zmiennej niezależnej Δx, tzn.

36. Pochodne wyższych rzędów:
Def. Niech funkcja f jest określona w otoczeniu pkt. x₀. Pochodną skończoną n - tego rzędu funkcji f w pkt. x₀ definiujemy indukcyjnie:

Pochodna II rzędu interpretacja fizyczna:
fizyczną interpretacją pochodne II rzędu jest przyspieszenie punktu materialnego:

37. Twierdzenie Rolle'a o wartości średniej i interpretacja geometryczna:
Jeżeli funkcja f:
• jest ciągła na przedziale domkniętym [a,b]
• ma pochodną na przedziale otwartym (a,b)
• f(a)=f(b)
wtedy istniej punkt c z (a,b), w którym pochodna f'(c)=0
Równość f'(c)=0 oznacza, że styczna do wykresu f=f(x) w pkt. (c,f(c)) jest równoległa do osi x.
38. Twierdzenie Lagrange'a o wartości średniej i interpretacja geometryczna:
niech funkcja f
• jest ciągła na przedziale domkniętym [a,b]
• ma pochodną na przedziale otwartym (a,b)
wtedy istnieje c należące do (a,b), w którym pochodna



39. Wnioski z twierdzenia Lagrange'a (monotoniczność, o tożsamości, o nierównościach):
• o monotoniczności: niech I oznacza dowolne przedziały, wtedy dla każdego x należącego do I f spełnia warunki:
- f'(x)=0 funkcja stała
- f'(x)>0 funkcja rosnąca
- f'(x)<0 funkcja malejąca
- f'(x)≥0 funkcja niemalejąca
- f'(x)≤0 funkcja nierosnąca
• o tożsamości: niech funkcje f i g będą określone na przedziale I i pkt. x₀ należy dętego przedziału. Jeżeli spełnione SA warunki:
- f(x₀)=g(x₀)
- f'(x)=g'(x)
to f(x)=g(x)
• o nierówności: niech funkcje f i g będą określone na przedziale I oraz niech x₀ jest punktem z tego przedziału. Jeżeli
- f(x₀)≤g(x₀)
- f'(x)≤g'(x)
to f(x)≤g(x)
40. Twierdzenie Cauchy'ego o wartości średniej:
niech funkcje f i g spełniają takie warunki:
• są ciągłe na przedziale domkniętym [a,b]
• mają pochodne na przedziale otwartym (a,b)
ponadto g'(x)≠0, wtedy istnieje takie c należące do (a,b), takie że

jest to uogólnienie twierdzenia Lagrange'a.
41. Reguła de L'Hospitala dla symbolu
:
niech funkcje f i g spełniają:
•
, przy czym g(x)≠0 dla x należącego do sąsiedztwa S(x₀)
• istnieje granica
, wtedy istnieje granica


42. Reguła de L'Hospitala dla symbolu
:
jeżeli:
•

• istnieje
, wtedy istnieje

43. Wzór Taylora z resztą Lagrange'a:
jeżeli funkcja f ma:
• pochodną ciągła rzędu n-1 na przedziale [x₀,x]
• pochodną skończoną rzędu n na przedziale (x₀,x)
to istnieje takie c należące do (x₀,x), taki że

uwaga: powyższe twierdzenie jest prawdziwe także dla przedziału [x₀,x] wtedy punkt c będzie z przedziału (x₀,x).Równość występująca w tym twierdzeniu nazywa się wzorem Taylora o wyrazie
z resztą Lagrange'a.
44. Ekstrema lokalne i twierdzenie Fermata o warunku koniecznym ekstremum:
Def. Funkcja f ma w punkcie x₀ minimum lokalne jeżeli istnieje δ>0, taki że
. Ona ma w pkt. x₀ maksimum lokalne jeżeli istnieje δ>0, taki ze

Tw. (o warunku koniecznym istnienia ekstremum Fermata)
Jeżeli funkcja f ma ekstremum lokalne w pkt. x₀ i pochodną f'(x₀) to pochodna f'(x₀)=0.
Uwaga: implikacja odwrotna jest fałszywa.
45. I warunek wystarczający istnienia ekstremum:
Jeżeli f'(x₀)=0 oraz istnieje δ>0, że f'(x)>0 dla x należącego do sąsiedztwa S(x₀^-,δ) i f'(x)<0 dla x należącego do sąsiedztwa S(x₀⁺,δ) to funkcja f ma w punkcie x₀ maksimum lokalne.
O minimum lokalnym analogicznie.

46. II warunek wystarczający istnienia ekstremum:
jeżeli f'(x₀)=0 a f''(x₀)>0 to funkcja f w pkt. x₀ ma minimum lokalne.
O maksimum analogicznie.
47. Algorytm szukania ekstremum globalnego:
Niech funkcja f będzie ciągła na przedziale [a,b] i ma pochodną skończoną wszędzie, możliwe poza skończoną liczba punktów. Ekstremum szukamy postępując następująco:
• znajdujemy punkty c₁…..c_n zerowania się pochodnej f'(x)=0 oraz punkty d₁…..d_m w których funkcja f nie ma pochodnej.
• obliczamy wartości funkcji w punktach końcowych a i b i w punktach c₁…..c_n i d₁…..d_m
• spośród liczb f(a), f(b), f(c₁)…f(c_n), f(d₁)….f(d_m) wybieramy najmniejszą m i największa M.
48. funkcja wypukła i wklęsła. Warunek wystarczający wypukłości:
Def. Funkcja f jest wypukła na przedziale (a,b) jeżeli dla każdej pary x,y liczb: a<x<y<b ma miejsce nierówność:

λ od 0-1.
Geometrycznie wypukłości oznacza, że każdy odcinek sieczny wykresu leży wyżej lub pokrywa się z fragmentem wykresu położonym między punktami przez które przechodzi sieczna.
Def. Funkcja f jest wklęsła na przedziale (a,b) jeżeli dla każdej pary x,y liczb: a<x<y<b ma miejsce nierówność:

Geometrycznie wklęsłość oznacza, że każdy odcinek sieczny wykresu leży niżej lub pokrywa się z fragmentem wykresu położonym między punktami przez które przechodzi sieczna.
Tw. (warunek wystarczający wypukłości)
• Jeżeli f''(x)>0 to funkcja f jest wypukła
• jeżeli f''(x)<0 to funkcja f jest wklęsła.
49. Punkty przegięcia warunek konieczny:
Def. Niech funkcja f będzie określona przynajmniej na otoczeniu punktu x₀ i ma w tym punkcie pochodną. Punkt (x₀,f(x₀)) jest punktem przegięcia p.p. wykresu funkcji g gdy istnieje δ>0, że f jest wypukła na sąsiedztwie lewostronnym S(x₀^-,δ) i f jest wklęsła na sąsiedztwie prawostronnym S(x₀⁺,δ) albo odwrotnie.
Tw. (warunek konieczny punktu przegięcia)
Jeżeli (x₀,f(x₀)) jest punktem przegięcia wykresu funkcji f i istnieje f''(x₀), to f''(x₀)=0.
Wniosek: funkcja może mieć punkty przegięcia jedynie w punktach zerowania się jej drugiej pochodnej albo w punktach, w których ta pochodnia nie isnieje.



50. I warunek wystarczający punktu przegięcia):
Jeżeli funkcja f ma pochodną w punkcie x₀ oraz istnieje δ>0, że f''(x)<0 dla każdego x należącego do S(x₀^-,δ), a f''(x)>0 dla każdego x należącego do S(x₀⁺,δ), to punkt (x₀,f(x₀)) jest punktem przegięcia p.p.
50. II warunek wystarczający punktu p1zegięcia:
Jeżeli f''(x₀)=0 a f'''(x₀)≠0 to punkt (x₀,f(x₀)) jest punktem przegięcia p.p.

Warunki dla pochodnych			Własności f
f'	f''	f'''
f'(x)>0	f''(x)>0		rosnąca wypukła
f'(x)>0	f''(x)<0		rosnąca wklęsła
f'(x)<0	f''(x)>0		malejąc wypukła
f'(x)<0	f''(x)<0		malejąca wklęsła
f'(x0)=0	f''(x0)>0		minimum lokalne
f'(x0)=0	f''(x0)<0		maksimum lokalne
	f'”(x0)=0	f'''(x0)≠0	punkt przegięcia

52. Asymptota pionowa. Warunek istnienia:
Def. Prosta x=x₀ jest asymptotą pionowa lewostronną jeżeli

podobnie z prawostronną.
Def. Asymptota pionowa obustronna. Prosta x=x₀ jest asymptota pionową obustronną lub krótka asymptotą pionową funkcji f jeżeli jest jednocześnie jej asymptotą lewostronną i prawostronną.
Tw. Funkcja elementarna może mieć asymptoty pionowe jedynie w skończonych krańcach dziedziny, które do niej nie należą.
53. Asymptota ukośna, pozioma. Warunek istnienia:
Def. Prosta y=Ax+B jest asymptotą ukośną dla funkcji f w pkt. +∞ gdy

obrazowo prosta jest asymptotą ukośną gdy jej wykres dla argumentów bardzo wielkich prawie pokrywa się z tą prostą. Podobnie definiuje się asymptotę ukośną w -∞.
Jeżeli A dla asymptoty ukośnej =0 wtedy mówimy, że asymptota jest pozioma. Warto podkreślić, że asymptota ukośna może przecinać wykres funkcji f nieskończenie wiele razy.
Tw. (warunek istnienia asymptoty ukośnej)
prosta y=Ax+B jest asymptotą ukośną funkcji f na +∞ jeżeli

Tw. (warunek istnienia asymptoty poziomej)
prosta y=B jest asymptotą poziomą dla funkcji f na +∞ jeżeli

54.Algorytm badania funkcji

1. Ustalenie dziedziny f-cji

2. Wskazanie podstawowych własności f-cji

a)parzystość lub nieparzystość

b)okresowość

c)miejsca zerowe

d)ciągłość

3. Obliczanie granic lub wartości f-cji na krańcach dziedziny

4. Znalezienie asymptot pionowych i ukośnych

5. Zbadanie I-wszej pochodnej

a)wyznaczenie dziedziny pochodnej i obliczenie

b)wyznaczenie punktów, w których f-cja może mieć ekstremum

c)wyznaczenie przedziału monotoniczności f-cji

d) ustalenie ekstremów

e)obliczenie granic lub wartości f-cji na krańcach jej dziedziny

6. Zbadanie II pochodnej

a)obliczenie II pochodnej

b)wyznaczenie miejsc, w których f-cja może mieć punkty przegięcia

c) ustalenie przedziałów wklęsłości i wypukłości

d)wyznaczenie punktów przegięcia

e) obliczenie wartości w punktach przegięcia

7. Wykres funkcji

55.Funkcja pierwotna, wniosek z twierdzenia Lagrange'a, warunek wystarczający istnienia f-cji pierwotnej

Def. Funkcja F jest funkcją pierwotną dla funkcji f na przedziale I jeżeli jej pochodna F'(x)=f(x) dla każdego x należącego do I

Z tw, Lagrange'a można wysnuć taki wniosek:

Niech F jest funkcją pierwotną dla f na przedz. I wtedy:

1) G(x)=F(x)+C także będzie funkcją pierwotną dla funkcji f

2)Każda f-cja pierwotna dla f-cji f na tym przedziale I ma postać F(x)+C (C-dowolna stała liczba)

Tw.(Warunek wystarczający istnienia funkcji pierwotnej)

Każda f-cja ciągła na przedziale ma f-cję pierwotną na tym przedziale

Uwaga: F-cja pierwotna dla elementarnej nie musi być elementarna
56. Całka nieoznaczona. Twierdzenie o pochodnej całki nieoznaczonej.

Def: Niech F będzie funkcją pierwotną dla funkcji f . Całką nieoznaczoną funkcji f na przedziale I nazywamy zbiór funkci {F(x)+c: c∈R}. Całkę nieoznaczoną funkcji f oznaczamy przez ∫f (x)dx.

Działania na całkach nieoznaczonych oznaczają działania na funkcjach pierwotnych reprezentujących tę całkę.

Twierdzenie o pochodnej całki i całce pochodnej.

Niech funkcja f na funkcję pierwotną na przedziale I wtedy:

1) ∀x∈I [∫f(x)dx]'=f(x)

2) ∫f'(x)dx=f(x) +c

57. Całki nieoznaczone ważniejszych funkcji elementarnych.

∫0dx=c

(α≠-1)

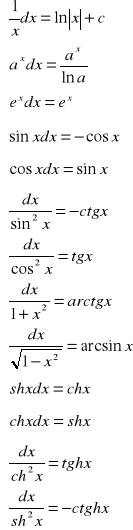
58. Twierdzenie o liniowości całki i o całkowaniu przez części.

Tw o liniowości całki

Jeżeli funkcje f i g mają funkcje pierwotne to całka ∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx

∫a⋅f(x)dx=a∫f(x)dx ∀a≠0.

Tw o całkowaniu przez części

Jeżeli funkcje f i g mają ciągłe pochodne w x∈I wtedy ∫f(x)g'(x)dx=f(x)⋅g(x)-∫f'(x)g(x)dx

59. Twierdzenie o całkowaniu przez podstawianie t=ϕ(x) i x=ϕ(t).

tw t=ϕ(x)

Jeżeli:

1. funkcja f:T→R ma pochodną ciągłą na przedziale T

2. funkcja ϕ:X→T ma pochodną ciągłą na X

∫f(ϕ(x))dx=F(ϕ(x))+c gdzie F jest pierwotna dla funkcji f.

inna postać twierdzenia: Niech mamy obliczyć ∫f(ϕ(x))⋅ϕ'(x)dx= robimy podstawienie t=ϕ(x) wtedy zgodnie z symboliką przyjmujemy w rachunku różniczkowym dt=ϕ'(x)dx =∫f(t)dt obliczamy ostatnią całkę i podstawiamy t=ϕ(x).

tw o całkowaniu przez podstawienie x=ϕ(t)

1. jeżeli funkcja ϕ jest różniczkowalna i różnowartościowa na przedziale T i przekształca go na X.

2.funkcja f ma na przedziale X funkcję pierwotną F to prawdziwe jest na tym przedziale ∫f(x)dx=[f(ϕ(t)⋅ϕ'(t)]⋅ϕ^-1

∫f(x)dx=∫f(ϕ(t))ϕ'(t)dt

pamietając, że po wyznaczeniu prawej strony otrzymamy wynik należy złożyć

60. Funkcja wymierna, właściwa. Ułamki proste 1go i 2go rodzaju.

Def:

Funkcję wymierną W(x) nazywamy właściwą gdy stopień wielomianów w liczniku jest mniejszy od stopnia wielomianu w mianowniku.

Uwaga: każdą funkcję wymierną niewłaściwą można przedstawić w postaci wielomianu funkcji wymiernej właściwej.

Def: funkcję postaci
nazywamy ułamkiem prostym pierwszego rodzaju, a funkcję postaci
nazywamy ułamkiem prostym II rodzaju
.

61. Twierdzenie o rozłożeniu funkcji właściwej wymiernej na ułamki proste.

Każdą funkcję wymierną właściwą można zapisać w postaci sumy ułamków prostych. Przedstawienie to jest jednoznaczne.

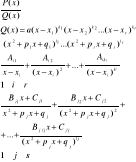
62. Całkowanie ułamków prostych 1go rodzaju.

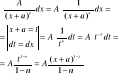
n≠1

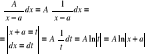
63. Całkowanie ułamków prostych 2go rodzaju.

64. Algorytm całkowania funkcji wymiernych.

1). Funkcje wymierne zapisujemy w postaci sumy wielomianu i funkcji wymiernej właściwej.

2). Mianownik funkcji wymiernej właściwej rozkładamy na czynniki liniowe i kwadratowe nierozkładalne.

3). Zapisujemy rozkład teoretyczny funkcji wymiernej właściwej na ułamki proste I i II rodzaju

4). Znajdujemy nieznane współczynniki tego rozkładu.

5). Obliczamy całki poszczególnych składników rozkładu.

65. Całkowanie funkcji postaci R(sin x,cos x), R-funkcja wymierna.

Dla obliczenia całek postaci ∫R(sin x,cos x) stosujemy podstawienie następujące:

1) t=cosx gdy R(-u,v)=-R(u,v)

2) t=sinx gdy R(u,-v)=-R(u,v)

3) t=tgx gdy R(-u,-v)=R(u,v)

4)
← podstawienie uniwersalne

66. Całkowanie sinax⋅cosbx; sinax⋅sinbx; cosax⋅cosbx.

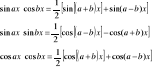
67. Całkowanie funkcji z niewymiernościami.

R(u,v) będzie funkcją wymierną dwóch zniennych u i v

Dla obliczenia całek:

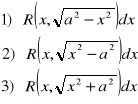
stosujemy

1) x=a sin t

2) x=a ch t

3) x=a sh t

68. Przestrzeń metryczna. Aksjomaty.

Def: Przestrzenią metryczną nazywamy zbiór X, któremu przyporządkowano funkcję dwóch zmiennych d(x,y) x,y∈Rx spełniającego następujące warunki (zwane aksjomatami):

1) d(x,y)≥0 oraz d(x,y)=0 x=y (aksjomat tożsamości)

2) d(x,y)=d(y,x) (aksjomat symetrii)

3) d(x,y)≤d(x,z)+d(z,y) ∀x,y,z∈X (aksjomat nierówności trójkąta)

Elementy przestrzeni metrycznej nazywamy PUNKTAMI. Funkcję d nazywamy METRYKĄ, liczbę d(x,y) nazywamy ODLEGŁOŚCIĄ MIĘDZY PUNKTAMI x i y.

Najprostszym przykładem przestrzeni metrycznej jest zbiór liczb rzeczywistych X=R z metryką d(x,y)=|x-y|

1) d(x,y)≥0

|x-y|=0<=>x-y=0<=>x=y

2) d(x,y)=|x-y|=|-(y-x)|=|y-x|=d(y,x)

3)d(x,y)=|x-y|=|x-z+z-y|≤|x-z|+|z-y|=d(x,z)+d(z,y)

69. Przestrzeń Rⁿ.

Elementem przestrzeni Rⁿ są wszystkie uporządkowane układy liczb rzeczywistych (x₁,x₂,….,x_n). Układy te nazywamy punktami tej przestrzeni, a same liczby x₁,x₂,….,x_n współrzędnymi prostokątnymi tych punktów. Odległość d(A,B) między punktami A=(a₁,a₂,….,a_n) B=( b₁,b₂,….,b_n) przestrzeni Rⁿ określamy

Gdy n=2 otrzymamy odległość na płaszczyźnie

70.Otoczenie i sąsiedztwo w przestrzeni metrycznej.

Otoczeniem o(x,r) punktu x przestrzeni metrycznej X o promieniu r jest zbiorem wszystkich punktów y∈X, dla których d(y,x)<r

SĄSIEDZTWEM S(x,r) punktu x przestrzeni metrycznej X o promieniu r jest zbiorem wszystkich punktów y∈X, dla których 0<d(y,x)<r

71. Zbiór otwarty.

Punkt x przestrzeni metrycznej X nazywamy punktem wewnętrznym zbioru A⊂X jeżeli zbiór ten zawiera pewne otoczenie punktu x np.

1) każdy punkt przediału (a,b)przestrzeni R jest punktem wewnętrznym.

2) punkt a przedziału [a,b] nie jest wewnętrznym

def: Zbiór, którego każdy punkt jest wewnętrznym nazywamy zbiorem otwartym.

Np. zbiór (a,b) jest otwarty w R.

72. Ciąg zbieżny i zbiór domknięty. Punkt brzegowy.

Def: Mówimy, że ciąg x_n, element przestrzeni metrycznej X dąży do punktu x o tej samej przestrzeni metrycznej X i zapisujemy x_n→x ∨
jeżeli d(x_n,x)→0 gdy n→∞

Ciąg pkt. P_k przestrzeni metrycznej Rⁿ o współrzędnych P_k =( x₁^(k),x₂^(k),….,x_n^(k)) dąży do P=(x₁,x₂,….,x_n)

x₁^(k) → x₁

x₂^(k) → x₂

x₃^(k) → x₃ gdy k→∞

def: Zbiór A przestrzeni metrycznej X nazywamy domkniętym jeżeli x_n∈A ∧ x_n→x => x∈A

np. [0,1] domknięty w R

73. Krzywa elementarna. Otwarta i zamknięta. Obszar.

Def: Krzywą elementarną przestrzeni nazywamy zbiór wszystkich punktów tej przestrzeni P=(x₁,x₂,….,x_n) o współrzędnych

x₁= x₁(t)

x₂= x₂(t)

……..

x_n= x_n(t)

gdzie x₁(t), x₂(t),…, x_n(t) są funkcjami ciągłymi określonymi w przedziale (α,β)

Przy czym różnym wartościom zmiennej t∈(α,β) odpowiadają różne punkty P.

Przykład krzywej elementarnej: okrąg x=sint, y=cost, 0≤t≤2π

Krzywą elementarną nazywamy zamkniętą jeżeli x_i(α)= x_i(β) ∀i=1,2

Krzywą która nie jest zamkniętą nazywamy otwartą.

Obszar jest to taki zbiór otwarty, którego każde dwa punkty można połączyć krzywą elementarną całkowicie w nim zawartą.

74. przestrzeń unitarna. aksjomaty.

Def: Przestrzenią liniową L nazywamy przestrzeń unitarną jeżeli każdej uporządkowanej parze x,y∈L jest przyporządkowana liczba <x,y>∈R taka, że:

1)<x,x〉≥0

2)<α₁x₁+α₂x₂,y〉=α₁<x₁,y〉 +α₂<x₂,y〉 ∀ x_1,x₂,y∈L ∀α_1, α₂∈R

3) <x,y〉=<y,x〉 ∀ x,y∈L

liczby <x,y〉 nazywamy iloczynem skalarnym. Łatwo zobaczyć, że z aksjomatów 2 i 3 wynika:

2' <x,α₁y₁+α₂y₂〉=α₁<x,y₁〉 +α₂<x,y₂〉 ∀ x,y_1,y₂∈L ∀α_1, α₂∈R

def: Normy elementu x przestrzeni unitarnej określamy wzorem
wzór ten przypomina określenie długości wektora. Norma przestrzeni unitarnej na własności:

1)||x||≥0 ||x||≠0 x=0

2) ||α||=|α|⋅||x|| ∀α∈R ∀x∈L

3) ||x+y||=||x||+||y||

własność 3 zwana nierównością trójkąta wynika z nierówności Schwartza |<x,y〉|=||x||⋅||y||

76. ciąg Cauchiego. Przestrzeń zupełna. Przestrzeń Hilberta.

Def: Mówimy, że ciąg elem. x_n przestrzeni metrycznej, jest CIĄGIEM CAUCHIEGO gdy ∀ε>0 ∃N: n,m>N d(x_n,x_m)<ε Łatwo zobaczyć, że każdy ciąg zbierzny będzie ciągiem Cauchiego, ale nie zawsze ciąg Cauchiego jest zbierzny.

Def: Mówimy, że przestrzeń metryczna jest zupełna, gdy każdy ciąg Cauchiego w niej jest zbierzny. Np. przestrzeń Q liczb wymiernych jest niezupełna, a przestrzeń liczb wymiernych R jest zupełna.

Def: Przestrzeń HILBERTA

Przestrzeń unitarną, która jest zupełna, nazywemy przestrzenią Hilberta. Np. określony w Rⁿ iloczyn skalarny
P=(x₁,x₂,….,x_n), Q=(y₁,y₂,….,y_n) wzg. tego iloczynu skalarnego Rⁿ będzie przestrzenią Hilberta.

================================

114. Pole powierzchni obrotowej

Niech funkcja nieujemna f ma ciągłą pochodną na przedziale [a,b]. Wtedy pole powierzchni Σ powstałej z obrotu wykresu funkcji f wokół osi ox wyraża się wzorem:

IΣI=2Π ∫ f(x)√1+[f`(x)]² dx

115. całka niewłaściwa w przedziale nieskończonym. definicje

Jeżeli funkcja f jest całkowalna przedziale [a,T]∀t>a

oraz ∃ granica skończona

lim T→∞ ∫ od a do T z f(x)dx (1)

to nazywamy ją całką niewłaściwą funkcji f na przedziale nieskończonym [a,∞]

i oznaczamy symbolem ∫ od a do ∞ z f(x)dx. Jeżeli granica nieskończona (1) istnieje to mówimy, że całka funkcji f w [a,∞] istnieje lub że ona jest nieskończona.

Jeżeli granica (1) nie istnieje to mówimy że całka niewłaściwa (1) jest rozbieżna.

116. Wartość główna na (-∞,∞):

wartością główną nazywamy granice:

v.p ∫ od -∞ do ∞ f(x) dx= lim T→+∞ z ∫od -T do T z f(x) dx

117. Kryterium porównawcze dla całki niewłaściwej

Na przedziale nieskończonym:

Jeżeli f(x) i g(x) są określone w [a,+∞) i całkowalne w każdym przedziale [a,T]∀T>a oraz 0<=f(x)<=g(x) to zbieżność ∫ od a do ∞ z g(x) dx (4)

zapewnia zbieżność ∫ od a do ∞ z f(x)dx (5) natomiast rozbieżność całki (5) zapewnia rozbieżność całki (4).

118 Bezwzględna i warunkowa zbieżność

w przedziale nieskończonym:

Całkę zbieżną ∫ od a do∞ z f(x) dx (7) nazywamy bezwzględnie zbieżną

jeżeli zbieżna jest ∫ od a do ∞ z | f(x)| dx (8).

Całka (7) nazywa się warunkowo zbieżna jeżeli całka (7)

jest zbieżna a całka (8) rozbieżna.

119. Całka niewłaściwa funkcji nieograniczonej:

Niech f określona na (a,b] jest nieograniczona w lewostronnym sąsiedztwie pkt.b. Jeżeli istnieje granica skończona lim ε→0⁺ z ∫ od a do b-ε z f(x)dx, to nazywamy ją całką niewłaściwą funkcji f w przedziale [a,b), i oznaczamy symbolem takim jak całkę Reymana ∫ od a do b z f(x)dx. Analogicznie określamy całkę niewłaściwą funkcji f która jest określona w (a,b] nieograniczoną w prawostronnym sąsiedztwie pkt.a

i całkowalną w prawostronnym przedziale [a+ε,b],ε>0 mianowicie:

∫ od a do b z f(x)dx= lim przy ε→0⁺ ∫ od a+ε do b f(x)dx

120. Wartość główna całki funkcji nieograniczonej:

v.p ∫ od a do b f(x)dx= lim przy ε→0⁺ [ ∫od a do c-ε f(x)dx + ∫ od c+ε do b f(x)dx]

121. Bezwzględna i warunkowa zbieżność

całki funkcji nieograniczonej:

Całkę niewłaściwa zbieżna drugiego rodzaju ∫ od a do b f(x)dx (1) nazywamy bezwzględnie zbieżną jeżeli jest zbieżna ∫ od a do b If(x)I dx (2). Całkę zbieżną (1) nazywamy warunkowo zbieżną jeżeli całką (2) jest rozbieżna.

122.podstawoweDef całki podwójnej w prostokącie:

Jeżeli dla każdego normalnego ciągu podziału prostokąta P ciąg sum całkowalnych Sn jest zbieżny do tej samej granicy skończonej i niezależnej od wyboru pkt. Ak to te granice nazywamy całką podwójną funkcji f w prostokącie P

i oznaczamy ∫∫ f(x)dσ (1)

∫∫ f(x,y)dσ= lim przy σn→0 ∑ od k=1 po n f(Ak)∆σk (2). Jeżeli całka (1) istnieje to mówimy że funkcja f jest całkowalna w sensie Reymana w prostokącie P.

123. Interpretacje geometryczne i fizyczne całki podwójnej:
• Interpretacja geometryczna Jeżeli funkcja f jest stała w prostokącie P f(x,y)=a, a>0 to dla każdego n:
, gdzie σ to pole P. Całka podwójna równa się objętości prostopadłościanu o polu podstawy σ i wysokości a.
Jeżeli funkcja f jest ciągła w prostokącie P i f≥0 to suma całkowa
równa jest sumie objętości prostopadłościanu o polach podstawy Δσ_k i wysokościach f(A_k). Całka
równa jest wówczas objętości bryły V ograniczonej płaszczyznami z=0, x=a, x=b, y=c, y=d.
• Interpretacja fizyczna: jeżeli funkcja P(x,y) jest gęstością powierzchniową masy prostokąta P, to całka
przedstawia masę tego prostokąta.
124. Twierdzenie o zamianie całki podwójnej na całkę iterowaną:
jeżeli funkcja f jest ciągła w prostokącie P, który jest określony wzorem
, to
, oraz

125. Obszar normalny. Całka podwójna w tym obszarze. Zbiór regularny.
zbiór domkniety D określony nierównościami
gdzie φ(x) i ψ(x) są funkcjami ciągłymi w przedziale [a,b], nazywamy obszarem normalnym względem osi X.
Rozważmy prostokąt

gdzie c=inf φ(x) w przedziale [a,b] a d=sup ψ(x) w przedziale [a,b]. Niech f(x,y) będzie funkcją ciągła w obszarze D, rozważamy funkcję f^*(x,y) określoną w prostokącie P następująco:

całkę podwójną funkcji f(x,y) w tym obszarze normalnym D oznaczamy symbolem

lub posługując się wzorem na zamianę całki podwójnej na całkę iterowaną:

Zbiór D nazywamy regularnym jeżeli jest on sumą
obszarów normalnych względem X lub Y, które nie mają wspólnych punktów wewnętrznych.
• Interpretacja geometryczna: niech funkcja f(x,y) będzie funkcja ciągłą w obszarze regularnym D, przy czym f(x,y)≥0.
Całka
przedstawia objętość bryły o podstawie D ograniczonej powierzchnią będącą wykresem funkcji f, oraz powierzchnią walcową utworzoną z prostych równoległych do osi Z i przechodzących przez brzeg obszaru D.
• Interpretacja fizyczna: jeżeli ρ(x,y) jest gęstością powierzchniową masy obszaru regularnego D, to całka

przedstawia masę m tego obszaru regularnego D.
Całki:
przedstawiają momenty statyczne M_x i M_y względem osi X i Y naszego obszaru D.
126. Zmiana zmiennych w całce podwójnej. Jakobian:
zmiana zmiennych w całce podwójnej ściśle związana z odwzorowaniem zbioru płaskiego za pomocą pary funkcji. Rozważmy pary funkcji ciągłych x= x(u,v) i y= y(u,v), które przekształcają zbiór D₀ w płaszczyźnie OUV w zbiór D w płaszczyźnie XYZ, wzajemnie jednoznacznie. Jakobianem nazywamy funkcję:


- odwzorowanie to przekształca wzajemnie jednoznacznie obszar regularny D₀ na obszar regularny D
- funkcje te są klasy C¹ w obszarze D₀
- funkcja f(x,y) jest ciągła w obszarze D
- jakobian J(u,v) przekształcenia nie równa się 0 w obszarze D₀
wtedy ma miejsce takie wzór:


127. Wyprowadzenie zmiennych biegunowych w całce podwójnej:
x= rcosθ, y= rsinθ, wtedy jakobian tego przekształcenia:

128. Całka potrójna w prostopadłościanie. Podstawowe definicje:
Rozważmy prostopadłościan
oraz funkcję f(x,y,z) określoną w tym prostopadłościanie. Dzielimy P na n prostopadłościanów P_k 1≤k≤n o objętościach ΔV_k. Podział ten oznaczmy symbolem Δn. Niech d_k oznacza długość przekątnej prostopadłościanu P_k. Liczbę δ_n która równa się max d_k nazywamy średnicą podziału d_k.
Jeżeli dla każdego ciągu normalnego podziału prostokąta P, sumę S_n zmieniają się do tej samej granicy skończonej, niezależnej od wyboru punktu A _k, to tą granicę nazywamy całka potrójną funkcji f w prostokącie P.

129. Interpretacje geometryczne i fizyczne całki potrójnej:
• Interpretacja geometryczna: Jeżeli f(A)≡1 to całka
przedstawia objętość prostopadłościanu P.
• Interpretacja fizyczna: Jeżeli ρ(A) jest gęstością masy prostopadłościanu P, to całka

przedstawia masę tego prostopadłościanu.
130. Zamiana całki potrójnej na całkę iterowaną:
Jeżeli funkcja f jest ciągła w prostopadłościanie P
to całka potrójna

--------------------------------------------------

139. Twierdzenie o niezależności całki krzywoliniowej od kształtu drogi całkowania. Wnioski:
Jeżeli funkcja P(x,y) i Q(x,y) są klasy C¹ w obszarze jednospójnym D, to spełnienie równości Q^'_x=P^'_y (2) w każdym punkcie w obszarze D jest warunkiem koniecznym i wystarczającym na to, żeby całka
po krzywej AB nie zależała od kształtu tej krzywej tylko od punktów A i B.

Wn: (4)1.jeżeli funkcje P i Q są klasy C¹ i spełniają warunek 2 to
=0 po krzywej C, która jest kawałkami gładka i zamkniętą i należy do d równa się 0.

2. Jeżeli funkcja P(x,y) i Q(x,y) są klasy C¹ w obszarze jednospójnym D oraz
kawałkami gładkiej krzywej zamkniętej C należącej do D spełniony jest warunek 4 w każdym punkcie tego obszaru to spełniony jest warunek 2.

140. Warunek istnienia funkcji z danymi pochodnymi cząstkowymi:
przypuśćmy, że funkcje P(x,y) i Q(x,y) są klasy C¹ w obszarze
, czy istnieje w tym obszarze funkcja U(x,y) dla której U'_x=P i U'_y=Q, przypuśćmy, że taka funkcja istnieje wtedy: U''_xy=P'_y i U''_yx=Q'_x, ponieważ funkcje P i Q są klasy C¹ więc drugie pochodne mieszane są równe sobie. Warunek Q'_x=P'_y jest konieczny dla istnienia U(x,y), okazuje się, że warunek ten jest wystarczający.
Rozważmy funkcję:
, gdzie (x₀,y₀) ustalony punkt należący do D.
U'_x=P(x,y)
U'_y=

141. Całka krzywoliniowa niekierowana. Podstawowe definicje:
Jeżeli
normalnego ciągu podziału przedziału [α,β] ciąg sum s_n=
jest zbieżny do tej samej granicy skończonej, niezależnie od wyboru punktu τ_k to tą granicę nazywamy całką krzywoliniową nieskierowaną:

=

142.Interpretacja geometryczna i fizyczna całki krzywoliniowej niekierowanej:
• interpretacja geometryczna: Jeżeli funkcja f(x,y)=1 to ciąg s_n=
zawsze równa się l. Jeżeli f(x,y)>0 i jest ciągła to
przedstawia pole powierzchni.
• interpretacja fizyczna: Jeżeli ρ(x,y) jest gęstością liniową masy krzywej L to
przedstawia masę tej krzywej.

143. Zamiana całki krzywoliniowej niekierowanej na całkę oznaczoną: Jeżeli funkcja f(x,y) jest ciągła na otwartej krzywej gładkiej L to całka
istnieje i jest równa

144. Całka powierzchniowa niezorientowana. Podstawowe pojęcia:
Jeżeli dla każdego normalnego ciągu podziału prostokąta P ciąg sum s_n jest zbieżny do tej samej granicy skończonej, niezależny od wyboru punktu A_k^' to tą granicę nazywamy całką powierzchniową niezorientowaną

=

=s_n

145.Interpretacja geometryczna i fizyczna całki powierzchniowej niezorientowanej:
• interpretacja geometryczna: Jeżeli F(x,y,z)=1 to
przedstawia pole płata gładkiego Ω 
• interpretacja fizyczna: Jeżeli ρ(x,y,z) jest gęstością powierzchniową masy pola Ω  to
przedstawia masę tego pola.

146. Obliczanie całki powierzchniowej niezorientowanej:
Jeżeli funkcja F jest ciągła na gładkim płacie Ω to
istnieje i oblicza się ją za pomocą wzoru
=

przykład :F(x,y,z)=z
Ω-tr. o wierzchołkach (1,0,0), (0,1,0), (0,0,1) f(x,y)=1-x-y

=

---