KRZYSZTOF MASSOPUST grupa IV MB 03-11-99r.

Sprawozdanie z ćwiczenia nr 6

1) W układach logicznych występują sygnały: „0” , „1”.

2) Suma logiczna jest to operacja dwóch lub większej ilości argumentów, której wynikiem jest „1” gdy jeden z argumentów jest „1”.

3) Iloczyn logiczny jest to operacja dwóch lub większej ilości argumentów , której wynikiem jest „1” gdy wszystkie argumenty są „1”.

4) Negacja jest zaprzeczeniem sygnału np.

a	ā
1	0
0	1

5) Wzory

a + b + c = a · b · c , a · b · c = a +b +c

6) Sprawdzenie prawdziwości drugiego wzoru:

a	b	c	a·b·c		a	b	c	a+b+c
0	0	0	1			1	1	1	1
0	0	1	1			1	1	0	1
0	1	0	1			1	0	1	1
0	1	1	1			1	0	0	1
1	0	0	1			0	1	1	1
1	0	1	1			0	1	0	1
1	1	0	1			0	0	1	1
1	1	1	0			0	0	0	0

7) Podstawowe własności:

a) przemienność mnożenia a·b =b·a

b) przemienność dodawania a+b = b+a

c) przemienność mnożenia względem dodawania a(b+c) = a·b + a·c

d) przemienność dodawania względem mnożenia a+b·c = (a+b)(a+c)

e) metoda uproszczenia tzw. „sklejania” a+a·b = a+b

8) Podstawowe wzory

a = a

a + 1 = 1

a + 0 = a

a + a = 1

a + a + a +...+ a = a

a · 1 = a

a · 0 = 0

a · a = 0

a · a · a · ... · a = a

a = a

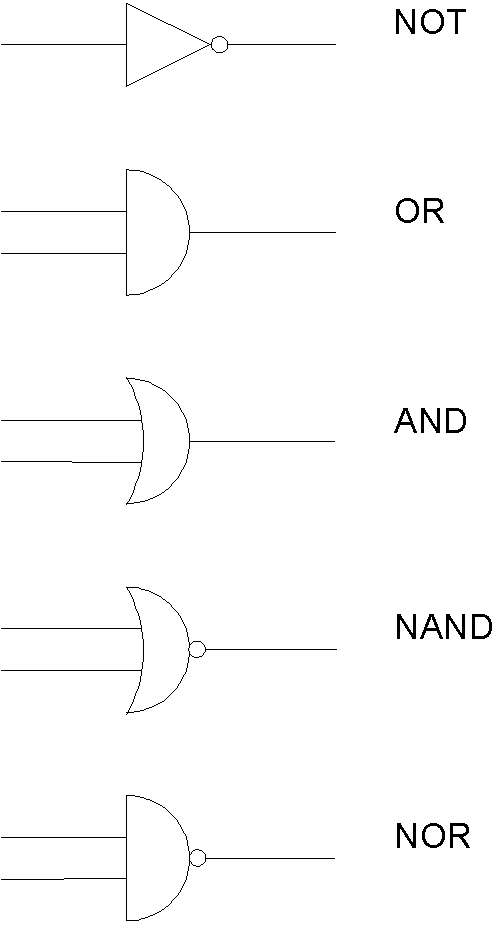
9) Podstawowe symbole stosowane schematach układów logicznych.

10) Rozpisanie układu logicznego przy pomocy schematu:

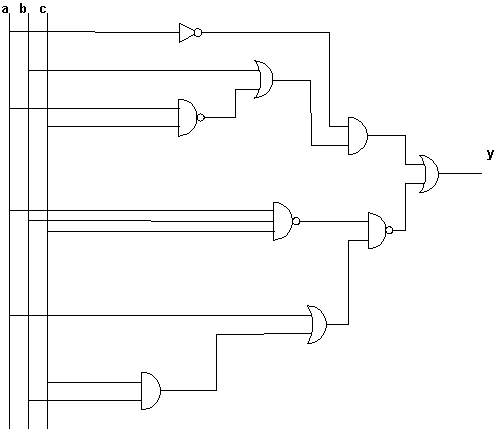
y = a( b + ac ) + abc( a + bc )

a	b	c	y
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

11) Zastosowanie uproszczeń

a) Dla układu o trzech sygnałach wejściowych

ab c	00	01	11	10
0	1	1	0	0
1	1	1	1	0

0 0 0

0 0 1

0 1 0 ā

0 1 1

0 1 1

1 1 1 ab

y = ā + ab

b) Dla układu o czterech sygnałach wejściowych

ab cd	00	01	11	10
11	1	1	0	1
10	1	1	0	1
00	1	1	0	1
01	1	1	0	1

0 0 1 1 1 0 1 1

0 0 1 0 1 0 1 0

0 0 0 0 1 0 0 0

0 0 0 1 1 0 0 1

0 1 1 1 0 0 1 1

0 1 1 0 0 0 1 0

0 1 0 0 0 0 0 0

0 1 0 1 0 0 0 1

y = a + b

ab cd	00	01	11	10
11	1	0	0	1
10	0	0	0	0
00	0	0	0	0
01	1	0	0	1

0 0 0 0

0 0 1 0

1 0 0 0

1 0 1 0

y = b · d

2

4

---