2. Redukcje pomiaru kątów poziomych z fizycznej powierzchni Ziemi na powierzchnię odniesienia.
Obliczenia związane z wyznaczeniem osnów geodezyjnych wykonujemy zwykle w obowiązującym systemie odniesień przestrzennych. Jednym z elementów tego systemu jest powierzchnia odniesienia. Obecnie wyniki pomiarów wykonanych na fizycznej powierzchni Ziemi odnosimy do elipsoidy GRS-80. W temacie tym zajmiemy się redukcją pomiarów kątów poziomych na tę powierzchnię. Redukcje te będą wykonywane poprzez obliczenie odpowiednich poprawek do obserwacji wykonanych na fizycznej powierzchni Ziemi. Jedną z zasadniczych przyczyn powodujących potrzebę wyznaczenia poprawek jest to, że obserwacje wykonywane na stanowisku przyrządu do punktów celowania związane są z kierunkiem pionu (kierunkiem siły ciężkości ) w tych punktach, natomiast jednoznaczne rzutowanie punktów fizycznej powierzchni Ziemi na powierzchnię odniesienia odbywa się za pomocą normalnych do tej powierzchni.
Najczęściej kierunek linii pionu nie pokrywa się z normalną do elipsoidy (Rys. 1)
Rys. 1 Odchylenie linii pionu od normalnej do elipsoidy
stąd wynika rozbieżność w rzutowaniu punktów, którą uwzględniamy w odpowiednich poprawkach redukcyjnych.
Teoretycznie do wyników pomiaru kierunków poziomych wykonanych na fizycznej powierzchni Ziemi wprowadzamy 3 poprawki redukcyjne:
poprawka z tytułu odchylenia pionu od normalnej w miejscu obserwacji (na stanowisku υu ,
poprawka z tytułu wysokości celu Hc nad elipsoidę υH i wynikającą stąd różnicę rzutowania punktu celowania na elipsoidę za pomocą normalnej i linii siły ciężkości,
poprawka z tytułu różnicy azymutów linii przekroju normalnego i linii geodezyjnej υG (Rys. 2). (Rys.
Rys.2 Azymuty linii geodezyjnej i przekrojów normalnych.
Linie geodezyjna jest obrazem rzutowanego odcinka z fizycznej powierzchni Ziemi na elipsoidę.
Poprawki wyżej wymienione można wyrazić następującymi wzorami:
![]()
(1)
![]()
(2)
![]()
(3)
ξ , η - składowe odchylenia pionu od normalnej,
Θ- azymut wypadkowej odchylenia,
A-azymut geodezyjny kierunku na punkt celowania
z-pomierzony kąt zenitalny na punkt celowania.
Poprawka υu najczęściej nie przekracza wartości 1” natomiast w terenach górskich może dochodzić do 2”; wyjątkowo nieco więcej.
Następna poprawka:
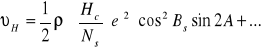
(4)
gdzie
Hc- wysokość punktu celowania nad elipsoidą,
Ns- promień krzywizny elipsoidy w punkcie rzutu ortogonalnego stanowiska na elipsoidę,
Bs- szerokość geodezyjna stanowiska,
A-azymut geodezyjny kierunku celowania,
e'2-kwadrat tzw. drugiego mimośrodu; dla elipsoidy GRS-80
e'2=0,67395·10-2
Poprawka υG dla długości celowych występujących w osnowach szczegółowych jest bardzo mała-zaniedbywalna. Dla długości celowej s=50 km, υG=0,007”.
Nadmieniamy, że podane wzory poprawek odnoszą się do kierunków, natomiast w odniesieniu do kątów należy brać różnicę poprawek dla obu kierunków wyznaczających kąt.
W rozpatrywanym temacie pojawiło się szereg pojęć z zakresu tzw. geodezji wyższej.
Zaniechano szczegółowo ich wyjaśnienia ze względu na i tak konieczną do ich zrozumienia szerszą wiedzę z tego przedmiotu. Dociekliwych odsyłamy do podręczników z geodezji wyższej .
Zagadnienie redukcji kątowych przedstawiono dlatego ażeby uzmysłowić studiującym, że taki problem istnieje podobnie jak analogiczny problem redukcji odległości rozpatrywany w następnym rozdziale.
Natomiast na ile jest to istotne zagadnienie dla pomiarów kątowych wykonywanych w poziomych osnowach szczegółowych przekonamy się na podstawie przykładu liczbowego.
P r z y k ł a d
Wyznaczyć maksymalne wartości poprawek kierunków poziomych mierzonych w osnowach szczegółowych na obszarze Polski.
R e a l i z a c j a
W Tatrach odchylenie pionu od kierunku normalnej może dochodzić do 10”;
przyjmując zatem:
u= 10” ; Θ-A=90° ; z=75°
i podstawiając do wzoru (2) otrzymamy:
υu=10” sin90°tg75°= 2,7”
Przy obliczeniu drugiej poprawki założymy:
Hc=2,5 km ; Ns=R=6382 km ; Bs=49°15' ; A=45° ; e'2=0,67395·10-2
Po wprowadzeniu tych wartości do wzoru (4) otrzymamy
![]()
Z przeprowadzonych obliczeń wynika, że tylko poprawka υu możesz być istotna dla redukcji pomiarów wykonywanych w terenach górskich obszaru Polski, natomiast druga poprawka υH może być zaniedbana w redukcji pomiarów kątowych wykonanych na całym obszarze Polski.
Przepisał Sebastian Gorgosz