Pracownia fizyczna
Ćwiczenie nr O2 Wyznaczanie ogniskowej soczewki metodą Bessela
IBC	Grupa 2	Masłyka Marcin Maliszewski Jacek Ńawrat Zbigniew
8.03.2001	Ocena:

Wstęp teoretyczny

Soczewką nazywamy bryłę przezroczystą materiału ograniczoną dwoma powierzchniami sferycznymi, których środki krzywizny leżą na jednej osi. Oś łącząca środki krzywizny obydwu powierzchni nazywamy osią optyczną soczewki. Wiązka promieni biegnących równolegle do osi optycznej, po przejściu przez soczewkę skupia się w jednym punkcie zwanym ogniskiem. Odległość ogniska od środka optycznego soczewki nazywamy odległością ogniskową f. W przepadku soczewek cienkich, środek geometryczny soczewki pokrywa się ze środkiem optycznym, przy soczewkach grubych następuje przesunięcie. Zależność odległości f od promieni krzywizny (r₁ i r₂ ) oraz od współczynnika załamania n materiału, z którego sporządzona jest soczewka, określona jest równaniem :

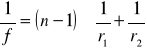
Promienie wychodzące z danego punktu P wskutek ich załamania w soczewce, zostają zebrane w innym punkcie P'. Punkt P' jest obrazem punktu P. Jeśli przedmiot P składa się z wielu punktów, wysyłających światło, to każdemu z nich można przyporządkować odpowiedni punkt obrazu. Jeżeli przedmiot znajduje się w odległości większej od ogniskowej, powstaje obraz rzeczywisty tego przedmiotu. Znaczy to, ze promienie, które wybiegły z jednego punktu zostaną ponownie przez soczewkę zebrane w jednym punkcie. Powstający obraz jest rzeczywisty i odwrócony. Jeżeli przedmiot znajduje się w odległości większej od podwójnej ogniskowej, obraz powstający jest pomniejszony. Jeżeli przedmiot znajduje się w odległości większej od ogniskowej, ale mniejszej od podwójnej ogniskowej, powstaje obraz rzeczywisty, odwrócony i powiększony. Obraz nazywamy rzeczywistym, gdy promienie załamane zbierają się w punkcie P', lub urojonym (pozornym), gdy zbierają się tam przedłużenia promieni. Dla soczewek cienkich odległość x przedmiotu od soczewki związana jest z odległością y obrazu od soczewki :

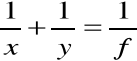
Wzór ten nazywamy wzorem soczewkowym. Określa on związek pomiędzy odległością przedmiotu od soczewki x , odległością obrazu od soczewki y i ogniskową ƒ.

Wyznaczanie odległości ogniskowej f metodą Bessela

Pomiar ogniskowej soczewki w oparciu o równanie soczewkowe jest obarczony błędem systematycznym, ponieważ nie znamy dokładnie środka optycznego soczewki. Dlatego skorzystamy z metody Bessela, która pozwala uniknąć błędów i jest bardzo prosta. Skorzystamy ze wzoru:

gdzie: l - odległość źródła światła od ekranu

d - różnica odległości pomiędzy położeniem przedmiotu w momencie, gdy obraz jest

powiększony z położeniem przedmiotu, gdy obraz jest pomniejszony.

Przebieg doświadczenia :

Wyznaczamy odległości przedmiotu od ekranu, soczewki od ekranu dla obrazu powiększonego i pomniejszonego. Pomiary powtarzamy dla pięciu różnych odległości przedmiotu od ekranu. Następnie dokonujemy pomiarów dla trzech różnych soczewek.

Dla ułatwienia wszystkie pomiary i obliczenia wykonywane są w centymetrach.

	Nr	d'	d"	d = d” - d'	l	f	fśr
Soczewka I	1	313,4	228,8	84,6	360	85,02	82,27
		2	302,4	229,4	73	350		83,69
		3	290,8	231,6	59,2	340		82,42
		4	279	232,8	46,2	330		80,88
		5	265,8	236,2	29,6	320		79,32
	Soczewka II	1	333,3	207,8	125,5	360		79,06	76,80
		2	323,3	207,8	115,5	350		77,97
		3	313,1	207,9	105,2	340		76,86
		4	303	208,2	94,8	330		75,69
		5	292,8	208,5	84,3	320		74,45
	Soczewka III	1	724,3	207,5	66,8	300		71,28	68,11
		2	264	207,7	56,3	290		69,77
		3	250,4	208,2	42,2	280		68,41
		4	242,5	209,3	33,2	270		66,48
		5	230,7	211,1	19,6	260		64,63

Obliczenia:

............................................................................................................................................................................................................................................................................................................. .....................................................................................................................................................................................................................................................................................................................................................................................................................................................................

....................................................................................................................................................... ....................................................................................................................................................... .....................................................................................................................................................................................................................................................................................................................................................................................................................................................................

....................................................................................................................................................... ....................................................................................................................................................... .....................................................................................................................................................................................................................................................................................................................................................................................................................................................................

....................................................................................................................................................... ....................................................................................................................................................... .....................................................................................................................................................................................................................................................................................................................................................................................................................................................................

....................................................................................................................................................... ....................................................................................................................................................... --> [Author:B]

Rachunek błędów:

Wykonywane przez nas pomiary są obarczone błędami wynikającymi z nie dokładności przyrządów pomiarowych i naszych zmysłów, czyli każdy pomiar może być wykonany tylko z pewną dokładnością. Otrzymane przez nas wyniki pomiarów nie dają nam prawdziwych wartości mierzonej wielkości lecz tylko przybliżoną. Te przybliżone wartości różnią się od rzeczywistych o pewna wielkość, która nazywamy błędem bezwzględnym. Błędem bezwzględnym jakiegoś pomiaru nazywamy różnicę między rzeczywistą wartością mierzonej wielkości, a wartością przybliżona otrzymana na drodze pomiarowej

....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Aby można było określić wpływ wielkości błędu bezwzględnego na wykonany pomiar określamy tzw. błąd względny, który oznaczamy literą δ. Błąd względny danej wielkości jest to stosunek błędu bezwzględnego do rzeczywistej wartości mierzonej wielkości. Bardzo często błąd względny podajemy nie w postaci ułamka, lecz wyrażamy w procentach.

...................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Przy dużej liczbie pomiarów średnia arytmetyczna jest bardzo bliska rzeczywistej wartości mierzonej wielkości. Aby powiązać współczynnik dokładności z wartością błędów wprowadzamy tzw. błąd kwadratowy, który jest miarą rozbieżności błędu wokół jego wartości oczekiwanej.

...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Wnioski :

Błędy wynikające z tej metody są bardzo małe. Są one spowodowane niedoskonałością wzroku ludzkiego. Dowodzi to, że ta metoda jest prawie idealna.

4

---