ROZWIĄZANIA ETAPU 1:

Klasy pierwsze

Niech
dowolne, takie że
i
.

Warunek
równoważny jest
.

=
=
=
=
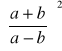
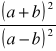
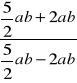
= 9.

Mogliśmy skrócić ułamek przez a i b, bo są to liczby różne od zera. Teraz pierwiastkując obie strony, otrzymujemy:

=3

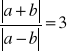
Korzystamy tutaj z faktu, że
.

Odp. 3

Klasy drugie

Funkcja
ma równomiernie rozłożone miejsca zerowe: 1, 2, 3, 4. Środek odcinka o końcach 1 i 4 wypada w punkcie o współrzędnych
.

Przesuńmy wykres funkcji f o 2,5 jednostki w lewo, otrzymując wykres funkcji g. Funkcje f i g będą miały to samo minimum.

=
.

Podstawmy teraz (dla łatwiejszej obserwacji) za
zmienną
.

dla
. Funkcja h - jest to funkcja kwadratowa.

Najmniejszą wartość przyjmie dla
.

.

Funkcja h będzie miała to samo minimum co funkcja h, a więc i funkcja f.

Odp. Najmniejsza wartość funkcji f to 9.

Klasy trzecie

Niech
.

Wtedy
.

Zwróćmy uwagę, że
.

. Korzystając z schematu Hornera obliczmy

	1	0	-3	-52
4	1	4	13	0

(
lub
).

Rozwiązaniem pierwszego równania jest 4, a drugie równanie jest sprzeczne
.

Odp.
, co należało udowodnić.