ROZWIĄZANIA ETAPU 3:

Klasy pierwsze

=
=
=
=
=
=
=
.

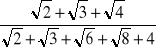
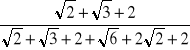
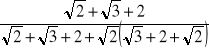
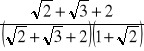
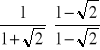
Odp.
.

Zadanie 3 dla klas drugich:

Niech
,
,
- liczby naturalne, takie że:
i
.

Wtedy
.

Z wzoru skróconego mnożenia wynika, że
.

Pamiętając, że
i
otrzymujemy układ równań (suma i różnica liczb naturalnych jest liczbą naturalną):

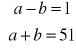
lub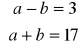
. Stąd

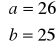
lub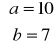
. Stąd

lub
.

Odp. 99.

Zadanie 3 dla klas trzecich:

Niech
. Wtedy nierówność
przyjmuje postać:
.

Szukamy pierwiastków trójmianu
. (rozwiązując równanie
).

Wyróżnik
. Zatem wykres funkcji
jest parabolą (której ramiona są skierowane do góry), która nie przecina osi
.

Z wykresu
można odczytać, że dla każdej liczby
funkcja
przyjmuje wartości dodatnie. Stąd nierówność
jest spełniona przez wszystkie liczby rzeczywiste x. Co należało udowodnić.

x

---