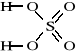
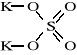
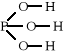
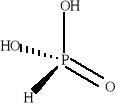
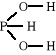
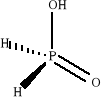
Chemia nieorganiczna - wstęp
Wstęp - geneza materii
Przedmiotem zainteresowania chemii nieorganicznej są pierwiastki i związki, a więc atomy i ich połączenia - cząsteczki. Nowoczesna chemia nieorganiczna stosuje tzw. podejście strukturalne, tj. tłumaczy właściwości pierwiastków i związków określonymi cechami budowy atomów i cząsteczek, innymi słowy - objaśnia właściwości materii przez jej budowę. Dochodzimy więc do stwierdzenia, że przedmiotem zainteresowania chemii nieorganicznej jest materia i to, jak jej budowa wpływa na jej właściwości. Przed szczegółową dyskusją zagadnienia korelacji budowy materii z jej właściwościami należałoby jednak zastanowić się, skąd w ogóle wzięła się materia, co wiąże się bezpośrednio z problemem powstania Wszechświata.
Znany ubiegłowieczny popularyzator nauki Hoimar von Ditfurth zatytułował jedną ze swych najbardziej znanych książek Na początku był wodór. Nie jest to jednak ścisłe podejście, w istocie bowiem wg obecnie obowiązującego paradygmatu naukowego, powstanie materii poprzedziła „era” energii. Na początku była zatem energia, a właściwie można nawet powiedzieć, że na samym początku było nie wiadomo co, ponieważ stan, z którego powstał Wszechświat, na razie wymyka się jakimkolwiek próbom dokładniejszego opisu. Mówiąc w uproszczeniu, stan taki nazywa się w fizyce punktem osobliwym. Stan ten uległ następnie przemianie określanej terminem „Wielki Wybuch”. Mówiąc w dużym uproszczeniu, był to proces nagłego wyemitowania ogromnych ilości energii, która to energia przechodziła następnie w materię i antymaterię, a te anihilowały ze sobą, dając na powrót energię, itd. W rezultacie pewnej przewagi materii nad antymaterią we Wszechświecie pozostała pewna ilość zwykłej materii, składającej się z ciężkich, względnie trwałych cząstek - barionów. Materia ta - materia barionowa - jest uznawana za materię wygenerowaną podczas Wielkiego Wybuchu. Cała istniejąca dziś we Wszechświecie materia stanowi produkty przemian tej materii początkowej, zachodzące w przestrzeni kosmicznej lub we wnętrzach gwiazd.
WAŻNE DATY W HISTORII WSZECHŚWIATA |
||
Czas |
Temperatura i typowa energia |
Możliwe zjawiska |
10-43 s |
1032K 1019 GeV |
grawitacja silna; konieczna kwantowa teoria grawitacji (na razie nieosiągalna) |
10-37 s |
>1029K >1016 GeV |
oddziaływania silne, elektromagnetyczne i słabe są zunifikowane |
10-33 s |
1027K 1014 GeV |
początek zamrażania procesów kontrolowanych przez bozony superciężkie; przypuszczalne ustanowienie przewagi materii nad antymaterią |
10-9 s |
1015K 102 GeV |
zamrażanie produkcji bozonów W; oddziaływania słabe słabną w porównaniu z elektromagnetyzmem (zakres energii osiągalny w zbudowanych ostatnio akceleratorach wysokich energii) |
10-2 s |
1013K 1 GeV |
siły kolorowe działające na kwarki i gluony grupują je, tworząc „białe" hadrony; siły koloru znikają z pola widzenia, powstają protony i neutrony |
100 s |
109K 1/10 MeV |
nukleosynteza - powstają hel i deuter |
106 lat |
103K 1/10 eV |
fotony oddzielają się od materii, powstaje promieniowanie tła (astronomia optyczna i elektromagnetyczna nie może spojrzeć w głąb czasu dalej niż do tej epoki) |
1010 lat |
3K 10-3 eV promieniowanie tła; gwiazdy stanowią lokalne gorące plamy |
dzień dzisiejszy - istnieją galaktyki i życie |
«1032 lat |
|
cała materia ulegnie erozji |
Dla porównania energie jonizacji większości atomów mieszczą się w przedziale od kilku do kilkudziesięciu eV. |
||
Źródło: Close, Kosmiczna cebula, PWN 1989. |
||
Pierwotna era życia Wszechświata była jednak erą dominacji energii i trwała do 100000 lat od Wielkiego Wybuchu. W erze tej dominowały cząstki przenoszące oddziaływania: bozony superciężkie i ciężkie, gluony (będące nośnikami sił międzykwarkowych) i wreszcie fotony (nośniki oddziaływań elektromagnetycznych). W swoistym tańcu energetycznym materii z antymaterią jako pierwsze cząstki powstały cząstki lekkie - kwarki i leptony, uważane dziś za „prawdziwe” cząstki elementarne, nie mające wewnętrznej struktury i nie dające się rozbić na mniejsze składowe. W miarę rozszerzania się Wszechświata spadała gęstość promieniowania, a zatem obniżała się i temperatura, co umożliwiało stopniowo tworzenie coraz bardziej złożonych struktur. Kwarki, związane siłami nazywanymi w fizyce „oddziaływaniami kolorowymi” (przenoszonymi przez gluony), połączyły się w cięższe cząstki - hadrony, takie jak proton i neutron. W miarę dalszego spadku temperatury do syntezy materii włączały coraz niżej energetyczne oddziaływania - najpierw doszło do nukleosyntezy, czyli łączenia się hadronów w jądra atomów cięższych od protu (wodoru-1). Gdy średnia energia we Wszechświecie spadła do poziomu niższego od energii dysocjacji, nastąpiła synteza atomów, przez połączenie się jąder atomowych z elektronami. Następnym etapem stała się synteza cząsteczek związków chemicznych i ta era trwa do dziś.
Powstanie pierwszych atomów, atomów wodoru, oznaczał początek drugiej ery życia Wszechświata, ery gwiazdowej. Fluktuacje gęstości materii powodowały formowanie się brył materii „odpornych” na działanie zewnętrznego promieniowania, a dalsza kondensacja tych brył doprowadziła do powstania gwiazd, co miało miejsce kilka milionów lat po Wielkim Wybuchu. Były to tzw. gwiazdy I generacji, których skład odpowiadał składowi materii pierwotnej, będącej bezpośrednim wynikiem Wielkiego Wybuchu. Materia pierwotna składała się w przeważającej ilości wodoru z dodatkiem niewielkiej ilości helu; zawierała też domieszki deuteru i litu. Wszystkie pozostałe pierwiastki i izotopy powstały w wyniku przemian termojądrowych we wnętrzu gwiazd lub przez te gwiazdy wywołanych.
Każda gwiazda I generacji (czyli powstała z materii wytworzonej w rezultacie Wielkiego Wybuchu) zaczyna swój cykl rozwojowy jako stopniowo zapadająca się pod wpływem własnej grawitacji kula gazowego wodoru. Zapadanie się materii w polu grawitacyjnym prowadzi do wytworzenia energii podgrzewającej materię, a gdy kompresja doprowadzi do powstania w centrum kuli odpowiedniej temperatury i ciśnienia, następuje zapłon - zainicjowanie syntezy termojądrowej wodoru w hel. Przemiana wodoru w hel nazywana jest ciągiem głównym; do gwiazd ciągu głównego należy też nasze Słońce.
Małe gwiazdy pod koniec spalania wodoru przechodzą bardziej burzliwy proces prowadzący przez etap czerwonego olbrzyma do białego karła, natomiast w przypadku gwiazd odpowiednio dużych (250% masy Słońca) po utworzeniu odpowiedniej ilości helu rozpoczyna się nukleosynteza węgla i tlenu. Jeśli masa gwiazdy jest mniejsza od 8 mas Słońca, kończy ona żywot gwałtownie jako supernowa, natomiast gwiazdy większe przechodzą kolejno stadia nukleosyntezy neonu, magnezu, krzemu i niklu. Końcowym etapem ewolucji gwiazdowej jest powstanie jądra żelaznego; żelazo, jako pierwiastek o najbardziej stabilnym jądrze atomowym, nie podlega już dalszym przemianom termojądrowym. Żelazowe jądro bardzo dużej gwiazdy zapada się, czemu towarzyszy eksplozja bardzo jasnej supernowej (zwanej niekiedy hipernową), połączona z rozpadem żelaza na hel. W trakcie wybuchów super- i hipernowych ma miejsce synteza pozostałych pierwiastków, które nie mogą powstać podczas zwykłego cyklu gwiazdowego (stąd wniosek, iż także życie na Ziemi, które nie może się bez takich pierwiastków obejść, zawdzięcza swoje istnienie supernowym). Pozostałością po eksplozji jest gwiazda neutronowa lub czarna dziura - obiekt o bardzo silnym polu grawitacyjnym skoncentrowanym w tak małych rozmiarach, że nie może z niego uciec nawet światło.
Cykl przemian termojądrowych, zachodzących we wnętrzu gwiazdy o odpowiednio dużej masie |
wodór → hel |
hel → węgiel, azot, tlen |
H, He, C, N, O → neon, magnez, nikiel |
wcześniejsze pierwiastki → żelazo |
Żyjemy wciąż w początkowym okresie ery gwiazdowej; wiek Wszechświata wynosi obecnie kilkanaście miliardów lat, zaś era gwiazdowa będzie trwać do chwili, gdy wiek Wszechświata będzie wynosić około 100 bilionów lat (100 milionów miliardów).
Jaka będzie przyszłość Wszechświata, a co za tym idzie - przyszłość materii? Z upływem czasu gwiazdy będą świecić coraz ciemniej, po czym nastąpi era degeneracji, w której większość gwiazd Wszechświata przekształci się z zdegenerowane pozostałości gwiazdowe, takie jak brązowe karły (obiekty gwiazdowe zbyt małe, by zapoczątkować syntezę wodoru w hel), białe karły (pozostałości małych gwiazd, takich jak Słońce), gwiazdy neutronowe (pozostałości wybuchów supernowych) i czarne dziury (pozostałości wybuchów największych supernowych i procesów kondensacji materii w centrach dawnych galaktyk). Era degeneracji jest erą ciemności i względnego zimna. Zachodzi w niej jednak sporo procesów generujących energię, tyle że rzadkich lub o niskiej wydajności. Do procesów tych należeć będą kolizje brązowych karłów, prowadzące do powstania „zwykłych”, świecących gwiazd (prowadzących nukleosyntezę), kolizje białych karłów, kończące się wybuchami supernowych, oraz - przede wszystkim - wychwyt i anihilacja ciemnej materii przez białe karły. Ciemna materia jest nie do końca jeszcze zidentyfikowaną, ale zasadniczą częścią materii zawartej we Wszechświecie, która nie emituje własnego promieniowania elektromagnetycznego, wobec czego nie możemy jej bezpośrednio zaobserwować. Wyniki badań prowadzonych w ostatnich latach sugerują, że w jej skład mogą wchodzić między innymi neutrina (bardzo słabo oddziałujące cząstki podobne do elektronów, tyle że pozbawione ładunku) oraz inne cząstki wysoce egzotyczne, których jak dotąd nie udało się otrzymać ani wykryć. Era degeneracji zakończy się rozpadem najbardziej trwałego hadronu - protonu.
Następnie rozpocznie się era czarnych dziur, w której jedynymi obiektami astronomicznymi będą właśnie czarne dziury - ciała o tak silnym polu grawitacyjnym, że nie może ich opuścić nawet światło. Będą one w tej erze jedynym źródłem energii. Jak to jednak możliwe, skoro nawet światło nie może ich opuścić? Odpowiedź przynosi współczesna fizyka kwantowa. Postuluje ona, że nawet doskonała próżnia nie jest absolutnie pusta - istnieją w niej tzw. cząstki wirtualne. Cząstkami tymi mogą być na przykład pary elektron - pozyton, generowane „z niczego” kosztem zaciągnięcia długo energetycznego, co jest możliwe w mikroświecie, którym nie rządzą zasady kategoryczne, a prawdopodobieństwa. Oczywiście cząstki powstałe „na kredyt” są ze sobą bardzo silnie związane, tak że anihilują ze sobą niemal natychmiast, generując dokładnie tyle energii, ile wynosi „dług” zaciągnięty na ich wytworzenie. Lecz jeśli taka para cząstek wirtualnych powstanie w pobliżu czarnej dziury, może się zdarzyć, że jedna z cząstek pary wpadnie do czarnej dziury. Absorpcja materii przez czarną dziurę jest procesem nieodwracalnym, więc druga cząstka z pary zostanie pozbawiona partnera do anihilacji. Będzie zatem istnieć niejako „przymusowo”, zaś energia na pokrycie „długu” zostanie pobrana z wnętrza czarnej dziury w chwili wnikania do niej pierwszej cząstki z pary. W ten sposób czarna dziura pozbędzie się części swojej energii.
W ostatecznym rozrachunku wszystkie czarne dziury wyparują w sposób opisany wyżej. We Wszechświecie pozostaną jedynie fotony o ogromnych długościach fali (rzędu średnicy całej galaktyki!), słabo oddziałujące z resztą materii neutrina oraz elektrony i pozytony, powstałe między innymi w wyniku procesu parowania czarnych dziur. Elektrony i protony będą się od czasu do czasu spotykać i tworzyć mało stabilne struktury „atomopodobne”, zwane pozytonium. Obiekty te, jako złożone z materii i antymaterii, będą jednak musiały prędzej czy później anihilować. Ostatecznym losem Wszechświata jest homogeniczna mieszanina neutrin i bardzo niskoenergetycznych fotonów.
Ery życia Wszechświata |
|||
Nazwa |
Czas |
Główne źródło energii |
Najważniejsze cechy |
Era pierwotna (energii) |
0 ÷ sto tysięcy lat |
Wielki Wybuch oraz anihilacja skondensowanej materii i antymaterii |
Bardzo wysokie temperatury, nieprzezroczystość - energii jest tyle, że droga swobodna fotonu jest znikomo mała. |
Era gwiazdowa (obecna) |
milion ÷ sto bilionów lat |
Synteza termojądrowa w gwiazdach (głównie wodór w hel) |
Temperatura od 1000K do 1K, przezroczystość, światło gwiazd. |
Era degeneracji |
tysiąc bilionów (1015) lat ÷ 1039 lat |
Anihilacja ciemnej materii we wnętrzach białych karłów |
Zimno i ciemno; pojedynczy biały karzeł generuje moc rzędu 400W; pod koniec następuje rozpad najbardziej trwałych ciężkich cząstek - protonów. |
Era czarnych dziur |
1040 ÷ 10100 lat |
Parowanie czarnych dziur |
Promieniowanie Hawkinga emitowane przez czarne dziury; jeszcze zimniej i jeszcze ciemniej. |
Ciemna era |
ponad 10100 lat |
Brak |
We Wszechświecie istnieją tylko elektrony i pozytony oraz bardzo niskoenergetyczne fotony i neutrina. |
Źródło: Adams, Laughlin, Ewolucja Wszechświata, PWN 2000 |
|||
Budowa materii
Pomijając wstępny etap, poprzedzający odkrycie pierwszej cząstki subatomowej - elektronu - historia badań nad budową materii stanowi wyrazisty przykład uzyskiwania coraz dokładniejszego wglądu w problem i coraz subtelniejszych wyników dzięki stosowaniu coraz bardziej wyrafinowanych i skomplikowanych metod badawczych. Odkrycia te wymuszały równocześnie odpowiednie doskonalenie teorii opisujących strukturę materii, co z kolei umożliwiło przewidywanie wielu nowych odkryć w tej dziedzinie. Jednym ze spektakularnych przykładów takiej predykcji było odkrycie neutrina w 25 lat po sformułowaniu przez Wolfganga Pauliego w 1931 roku postulatu o jego istnieniu; Pauli pragnął w ten sposób wyjaśnić niezgodną z wcześniejszymi teoriami utratę energii w rozpadzie neutronu.
Rozwój teorii budowy materii |
||
Data |
Etap |
Opis |
V wiek pne. |
Teoria atomistyczna Demokryta |
Koncepcja całkowicie teoretyczna - spekulacja filozoficzna niepoparta dowodami eksperymentalnymi. |
1805 |
Teoria atomistyczna Daltona |
Koncepcja teoretyczna mająca na celu wyjaśnienie określonych cech związków chemicznych, ale niepoparta dowodami eksperymentalnymi. |
1897 |
Odkrycie elektronu przez J.J.Thomsona |
Pozwoliło nie tylko wyjaśnić mechanizm zjawisk elektrycznych itp., ale dowiodło też, że atom nie musi być niepodzielny - może mieć strukturę wewnętrzną. Model atomu Thomsona: ciasto o ładunku dodatnim, nadziewane ujemnymi rodzynkami-elektronami. |
1911 |
Odkrycie jądra atomowego przez Rutherforda |
Uświadomiło, że materia w przeważającej części składa się z próżni. Planetarny model atomu (Rutherforda): jądro składające się z protonów i obiegane przez elektrony tak jak Księżyc obiega Ziemię. |
1913 |
Zastosowanie zasad mechaniki kwantowej przez Bohra |
Skwantowanie promieni „orbit” elektronów uniemożliwiło elektronom upadek na jądro (była to zasadnicza słabość planetarnego modelu Rutherforda). Pierwszy model atomu dobrze opisujący rzeczywistość - model Bohra. |
1932 |
Odkrycie neutronu przez Chadwicka |
Istnienie takiej cząstki było postulowane przez Rutherforda dla wyjaśnienia faktu, że na przykład masa atomu helu-4 jest cztery razy większa od masy atomu wodoru-1, ale atom ten zawiera tylko dwa elektrony, a więc i dwa protony. Z tego powodu musi zawierać dodatkowe cząstki obojętne elektrycznie. |
1936 |
Odkrycie mionu przez Andersona |
Odkrycie tego „rezerwowego elektronu” (mion przypomina elektron pod każdym względem z wyjątkiem masy, 200 razy większej) było zupełnie nieoczekiwane i nie udało się go wyjaśnić przez następne 40 lat. |
1947-50 |
Odkrycie pionów (mezonów π) przez Powella |
Stanowiło potwierdzenie koncepcji Yukawy, który postulował istnienie sił spajających jądro elektronowe, składające się z równoimiennych protonów i elektrycznie obojętnych neutronów (więc nie mógł za to odpowiadać elektromagnetyzm). |
1956 |
Odkrycie neutrina przez Reinesa i Cowana |
Istnienie takiej cząstki było postulowane w 1930/31 przez Pauliego dla wyjaśnienia faktu, że elektron i proton powstające w rozpadzie neutronu nie poruszają się dokładnie w przeciwnych kierunkach, ale pod kątem różnym od 180º - wobec tego musi im towarzyszyć jeszcze jedna cząstka. |
Od 1970 |
Model standardowy |
Model budowy materii tłumaczący różnorodność i obfitość cząstek subatomowych, a także ich budowę jako grup kwarków - „nowych” cząstek elementarnych postulowanych dla wyjaśnienia dysproporcji między rozmiarami elektronu i protonu, a następnie odkrywanych począwszy od lat 60. XX wieku. |
? |
Teoria wielkiej unifikacji |
Teoria jednocząca wszystkie oddziaływania - grawitację, elektromagnetyzm, oddziaływania silne i oddziaływania słabe w jednym opisie budowy materii. |
Opisując budowę materii należy przeanalizować dwa elementy: po pierwsze - składowe, które ją tworzą; a po drugie - siły, które spajają te składowe. Znane są obecnie cztery rodzaje oddziaływań; zgodnie z dualizmem korpuskularno-falowym każdemu z nich odpowiada określona cząstka lub cząstki, które są jego nośnikami, tj. transmitują to oddziaływanie między oddziałującymi elementami.
Podstawowe oddziaływania i ich nośniki |
||||
Typ |
Nośniki |
Zasięg |
Siła |
Charakterystyka |
Oddziaływanie grawitacyjne |
Grawitony? |
Nieskończony |
Słabe |
Działają przede wszystkim między ciałami makroskopowymi |
Oddziaływanie elektromagnetyczne |
Fotony |
Nieskończony |
Silne |
Odpowiadają za powstawanie wiązań chemicznych |
Oddziaływanie silne |
Piony |
10-14 m (skala jądra atomowego) |
Silne |
Wiążą protony i neutrony w jądrze |
Oddziaływanie kolorowe |
Gluony |
Poniżej 10-15 |
Silne |
Wiążą kwarki np. w protonach i neutronach |
Oddziaływanie słabe |
Bozony W i Z |
10-15 m (skala jądra atomowego) |
Słabe |
Odpowiadają za przemiany cząstek subatomowych i elementarnych, np. rozpad neutronu na proton i elektron albo przemianę neutrina w elektron |
|
Bozon X |
10-29 m |
Bardzo słabe |
Powoduje rozpad protonu? |
Materia składa się z atomów, które można nawet odpowiednimi metodami „sfotografować”, stosując do tego urządzenie zwane skaningowym mikroskopem tunelującym.
Atomy nie są jednak sztywnymi, litymi kulkami. Jak wykazało doświadczenie Rutherforda, każdy atom składa się z jądra otoczonego elektronami. Praktycznie cała masa atomu skupiona jest w jego jądrze, które zajmuje około jednej bilionowej całej objętości atomu, czyli 0,0000000001%! Resztę stanowi próżnia, wobec czego można się zastanowić, dlaczego materia wydaje się nam spoista i przeważnie twarda (zwłaszcza gdy jakiś przedmiot próbuje zająć miejsce, w którym znajduje się już inny przedmiot). Odpowiadają za to elektrony, a ściślej - tworzone przez nich wiązania i siły odpychania ładunków jednoimiennych. Wiązania między atomami tworzącymi dany przedmiot są odpowiedzialne za jego spoistość, natomiast twardość jest spowodowana odpychaniem się ładunków elektronów stykających się obiektów.
Cząstki składające się na atom nazywane są subatomowymi, jednak w rzeczywistości proton, neutron i elektron nie stanowią pełnej listy takich cząstek.
Klasyfikacja cząstek subatomowych |
||||
Grupa |
Charakterystyka |
Podgrupa/opis |
Przykłady |
Właściwości |
Leptony |
Nie odczuwają oddziaływań silnych |
Mają spin ½; mion i taon mają właściwości zbliżone do elektronu, tylko większe masy |
Elektron (negaton) |
trwały |
|
|
|
Neutrino (elektronowe) |
trwałe |
|
|
|
Mion |
τ ≈ 10-6 s |
|
|
|
Neutrino mionowe |
|
|
|
|
Taon |
τ ≈ 10-13 s |
|
|
|
Neutrino taonowe |
|
Hadrony |
Odczuwają oddziaływania silne |
Mezony - mają spin całkowity (0,1,2) (składają się z parzystej liczby kwarków) |
Pion (mezon π) |
τ = 10-8 s lub τ = 10-16 s |
|
|
|
Mezon η (eta) |
τ = 10-19 s |
|
|
|
Kaon (mezon K) |
τ = 10-8 s lub τ = 10-10 s |
|
|
Bariony - mają spin będący wielokrotnością ½ (składają się z nieparzystej liczby kwarków) |
Proton |
τ = 1032 lat |
|
|
|
Neutron |
τ ≈ 15 minut (swobodny) |
|
|
|
Rodzina Σ (sigma) |
τ = 10-10 s lub τ = 10-20 s |
|
|
|
Rodzina Λ (lambda) |
τ = 10-10 s |
|
|
|
Rodzina Ξ (ksi) |
τ = 10-23 s |
|
|
|
Rodzina Δ |
τ = 10-23 s |
|
|
|
Rodzina Σ* |
τ = 10-23 s |
|
|
|
Rodzina Ξ* |
τ = 10-23 s |
Leptony (całkowity ładunek elektryczny) i kwarki (ułamkowy ładunek elektryczny) składają się na grupę fermionów, cząstek rzeczywiście elementarnych, tj. nie mających wewnętrznej struktury i nie dających się rozłożyć na mniejsze cząstki. Wszystkie fermiony mają spin ½.
Każdy z fermionów ma swój odpowiednik „antymaterialny”, np. elektron - antyelektron (pozyton), neutrino - antyneutrino, kwarki - antykwarki. Ponadto kwarki różnią się od leptonów posiadaniem dodatkowej właściwości, podobnej do ładunku elektrycznego, a nazywanej kolorem - czerwonym, niebieskim lub żółtym. Właściwości tej nie obserwujemy u cząstek subatomowych złożonych z kwarków, ponieważ mezony składają się zawsze z pary kwark+antykwark tego samego koloru (co „znosi” kolor), a hadrony - z trzech kwarków wszystkich trzech kolorów (co daje „kolor biały”).
Budowa przykładowych barionów |
|||
Cząstka |
Skład kwarkowy |
Ładunek (obliczony na podstawie ładunku kwarków) |
Spin (obliczony na podstawie spinu kwarków) |
Pion+ |
górny+antydolny |
2/3 + 1/3 = 1 |
½ - ½ = 0 |
Kaon0 |
dolny+antydziwny |
-1/3 + 1/3 = 0 |
½ + ½ = 1 |
Proton |
górny+górny+dolny |
2/3 + 2/3 - 1/3 = 1 |
½ + ½ - ½ = ½ |
Neutron |
górny+dolny+dolny |
2/3 - 1/3 - 1/3 = 0 |
½ + ½ - ½ = ½ |
Rodzina kwarków w ujęciu satyrycznym: u - górny, d - dolny, c - powabny,
s - dziwny, t - wierzchni (prawdziwy, w chwili powstawania rysunku
jeszcze nie odkryty), b - spodni (denny)
Budowa atomu
Nieokreśloność mikroświata
W poprzednim wykładzie stwierdziliśmy, że grupa cząstek elementarnych obejmuje cząstki o połówkowym spinie, obdarzone zerowym (neutrina), jednostkowym (elektrony) lub ułamkowym (kwarki) ładunkiem elektrycznym. Kwarki, cząstki o ułamkowym ładunku, łączą się w większe cząstki subatomowe, z których najpopularniejszymi i najłatwiejszymi do zaobserwowania są proton i neutron. Protony i neutrony tworzą dodatnie jądra atomowe, o ładunku równym liczbie protonów, zwanej też liczbą atomową. Suma protonów i neutronów w jądrze atomu nazywa się liczbą masową. Liczby protonów i neutronów w jądrze nie są ze sobą powiązane, choć niektóre ich kombinacje są szczególnie korzystne energetycznie. Jądra parzysto-parzyste (czyli zawierające parzystą liczbę protonów i parzystą liczbę neutronów) są trwalsze od pozostałych, zaś szczególnie trwałe są te jądra atomowe, w których liczba protonów równa się liczbie neutronów.
Atom jako całość jest elektrycznie obojętny, więc dodatni ładunek jądra atomowego jest kompensowany przez elektrony otaczające to jądro. Jest oczywiste, że w obojętnym atomie liczba elektronów musi być równa liczbie protonów, a więc liczbie atomowej.
Zatem protony, neutrony i elektrony są najbardziej oczywistymi komponentami materii i z nich składają się atomy. Jakie jednak prawa rządzą tworzeniem atomów z cząstek subatomowych?
Należy w tym miejscu wspomnieć o dwóch faktach dotyczących mikroświata, w znaczący sposób odróżniających go od normalnie obserwowanego przez ludzi makroświata. Wśród zachowań cząstek subatomowych i atomów znajdziemy i takie, które świadczą o ich naturze falowej. Od dawna znana jest dwoistość opisu promieniowania elektromagnetycznego, które w pewnych aspektach lepiej opisuje się jako strumień cząstek - fotonów, a w innych - jako falę będącą zaburzeniem pola elektromagnetycznego. W trakcie badań nad elektronem okazało się jednak, że podobną dwoistość - dualizm korpuskularno-falowy - wykazują również cząstki subatomowe. Na przykład strumień elektronów ulega tak charakterystycznym falowym zjawiskom, jak dyfrakcja i interferencja. Wobec tego pęd - wielkość charakterystyczną dla cząstki (ciała materialnego) -można powiązać z długością fali:
p = h/λ
Skoro p = mv, to można wyprowadzić wzór na długość fali, odpowiadającej ciału o masie m, poruszającemu się z prędkością v, czyli fali de Broglie'a:
![]()
Jak widać z powyższego wzoru, długość fali materii jest odwrotnie proporcjonalna do masy poruszającego się ciała. Dlatego efekt dualizmu korpuskularno-falowego nie jest obserwowany dla ciał makroskopowych - mają one zbyt duże masy i odpowiadająca im fala materii ma zbyt znikomą długość. Natomiast elektronowi poruszającemu się z prędkością rzędu prędkości światła odpowiada fala o długości 10-10 m = 0,1 nm, porównywalna z wielkością atomów - dzięki temu właśnie atomy w sieci krystalicznej mogą działać jak siatka dyfrakcyjna i powodować rozpraszanie elektronów.
W oparciu o równanie de Broglie'a Schrødinger sformułował zasady mechaniki kwantowej, pozwalającej na opisanie fali materii dla cząstki poruszającej się w polu potencjału, czyli na przykład dla elektronu znajdującego się w polu elektrycznym jądra atomowego. Wg Schrødingera równanie fali materii pozwala obliczyć gęstość ładunku elektrycznego w danym punkcie przestrzeni. Elektron jest tu traktowany jako cząstka rozmyta. Obecnie jednak interpretuje się równanie Schrødingera (i same cząstki) statystycznie - elektron jest w tym ujęciu cząstką punktową, a kwadrat modułu funkcji falowej określa gęstość prawdopodobieństwa napotkania tej cząstki w danym fragmencie przestrzeni w danej chwili. Zastosowanie reguł statystyki wprowadza dodatkową nieokreśloność, zwaną zasadą nieoznaczoności Heisenberga. Zasada ta jest konsekwencją kwantowych właściwości mikroświata i mówi, że nigdy nie da się jednakowo pewnie określić położenia i prędkości cząstki. Granicę stanowi tu stała Plancka:
![]()
Z nierówności tej wynika, że im dokładniej wyznaczymy prędkość cząstki, tym mniej dokładnie ją zlokalizujemy. Stopień nieoznaczoności jest odwrotnie proporcjonalny do masy badanego ciała, przez co efektu tego nie obserwujemy w makroświecie.
Zasada nieoznaczoności wynika z prostego faktu, że na poziomie cząstek subatomowych sam akt pomiaru zaburza stan obserwowanej cząstki. W celu określenia położenia stołu w ciemnym pokoju musimy zapalić światło, czyli oświetlić ów stół strumieniem fotonów. Fotony, które odbiją się od stołu i dotrą do naszych oczu, dostarczą nam informacji o stanie stołu, tj. o jego prędkości i położeniu. Oczywiście będą one miały inną energię niż fotony padające na stół - część tej energii zostanie przekazana stołowi i wprawi go w ruch. Zgodnie z zasadą zachowania energii:
mfvf = msvs
zatem prędkość „ruchu” stołu można obliczyć ze wzoru:
![]()
Widać stąd, że ta prędkość jest odwrotnie proporcjonalna do masy stołu. Skoro masa fotonów jest znikomo mała w porównaniu z masą stołu, to i prędkość obserwowanego stołu zmieni się zaniedbywalnie. Innymi słowy - mimo bombardowania fotonami stół pozostanie na swoim miejscu, a my będziemy mogli określić zarówno jego położenie, jak i prędkość (równą 0 ze znakomicie wystarczającym przybliżeniem).
Inna sytuacja ma miejsce w przypadku elektronu, który ma masę porównywalną z fotonem. W celu zbadania położenia i prędkości fotonu musimy również „uderzyć” go fotonem. Foton ten pobierze informację o położeniu i prędkości badanego elektronu i dostarczy ją obserwatorowi - czyli po zderzeniu foton będzie mieć inną energię, niż przed. Ale ta zmiana energii nie może pozostać bez wpływu na elektron, znów z powodu zasady zachowania energii:
mfvf = meve
Zmieni się zatem zarówno energia fotonu, jak i elektronu. Foton przyniesie obserwatorowi informacje o stanie elektronu przed zderzeniem, jednak stan ten zmieni się w wyniku zderzenia i informacje przyniesione badaczowi przez foton będą już nieaktualne.
Funkcja falowa a zachowanie elektronu w atomie
Funkcja falowa Ψ opisuje zachowanie elektronu w atomie, przyjmując różne wartości w zależności od miejsca w przestrzeni. Jest więc funkcją zmiennych x, y i z, oznaczających współrzędne punktu w układzie kartezjańskim, w którego początku znajduje się jądro atomowe. Jak wspomnieliśmy, kwadrat modułu funkcji falowej |Ψ(x,y,z)|2 oznacza prawdopodobieństwo znalezienia elektronu w punkcie o współrzędnych x, y, z. Zbiór niezerowych wartości prawdopodobieństwa tworzy tzw. chmurę elektronową wokół jądra atomu. Wartość prawdopodobieństwa zależy od odległości, w której jest mierzone:
Jak widać, prawdopodobieństwo znalezienia elektronu zmierza asymptotycznie do zera w nieskończoności. O ile prawdą jest, że oddziaływania elektromagnetyczne (których częścią jest oddziaływanie elektrostatyczne między dodatnim jądrem a ujemnym elektronem) mają zasięg nieskończony, o tyle ze względów praktycznych przyjmuje się graniczną wartość prawdopodobieństwa, poniżej której prawdopodobieństwo znalezienia elektronu uznaje się za zaniedbywalne. W ten sposób „zasięg elektronu” kończy się w pewnej odległości od jądra atomowego. Przedstawiając to graficznie, otrzymamy powierzchnię graniczną:
Podsumowując - wg obecnie obowiązującego modelu atom składa się z jądra atomowego otoczonego elektronami, elektrony jednak nie są traktowane jako punktowe cząstki poruszające się po orbitach, tylko jako media rozproszone wokół jądra, a ich zachowanie i położenie jest opisywane przez funkcje zwane orbitalami i ich parametry - liczby kwantowe.
Orbitale atomowe i liczby kwantowe
Rozwiązanie równania Schrødingera pozwala znaleźć pewne funkcje własne tego równania. Funkcje te, zależne od zdefiniowanych parametrów n, l, m, nazywają się orbitalami, a parametry te - liczbami kwantowymi.
W mechanice kwantowej kwantowaniu podlega pięć właściwości elektronu w atomie (warto zauważyć, że elektron swobodny nie podlega już tak wielu ograniczeniom), a zatem jego stan opisuje pięć liczb kwantowych.
Główna liczba kwantowa
Główna liczba kwantowa o symbolu n może przyjmować wartości kolejnych liczb naturalnych 1,2,3,… teoretycznie do nieskończoności (w praktyce znamy pierwiastki, w których n przyjmuje wartości od 1 do 7).
Zbiór elektronów (stanów kwantowych) o tej samej wartości głównej liczby kwantowej nazywa się powłoką elektronową.
Kolejne powłoki elektronowe oznaczane są dużymi literami alfabetu łacińskiego, poczynając od K: K, L, M, N, P itd.
Główna liczba kwantowa kwantuje energię atomu (zasadniczo w atomie wodoru i helu, gdyż w przypadku atomów zawierających więcej niż dwa elektrony staje się niewystarczająca).
Energia elektronu w atomie wodoru określana jest następującym równaniem:
![]()
gdzie En - energia elektronu w stanie (na poziomie) n, n - główna liczba kwantowa, a E1 = 13,6 eV to bezwzględna wartość energii elektronu w stanie podstawowym.
Poboczna liczba kwantowa
Poboczna liczba kwantowa o symbolu l może przyjmować wartości kolejnych liczb całkowitych od 0 do n-1, czyli począwszy od powłoki L (n=2) może przyjmować więcej niż jedną wartość (w przypadku powłoki L: 0 i 1).
Zbiór elektronów o tej samej wartości pobocznej liczby kwantowej l nazywa się podpowłoką elektronową.
Podpowłoki oznaczane są małymi literami alfabetu łacińskiego. Wartości l=0 odpowiada podpowłoka s, wartości l=1 - podpowłoka p, wartości l=2 - podpowłoka d, wartości l=3 - podpowłoka f, zaś kolejnym podpowłokom - następne litery w kolejności alfabetycznej: g, h, i itd. W otrzymanych do tej pory atomach elektrony obsadzają podpowłoki s, p, d, f; teoretycznie rzecz biorąc obsadzanie podpowłoki g powinno się rozpocząć od pierwiastka o liczbie atomowej około 123, nie wiadomo jednak, kiedy uda się go otrzymać i zweryfikować to przypuszczenie.
Poboczna liczba kwantowa kwantuje moment pędu elektronu, a ściślej orbitalny moment pędu (związany z domniemanym ruchem elektronu wokół jądra atomowego). Moment pędu jest iloczynem masy obiektu, jego prędkości liniowej i promienia okręgu, jaki zakreśla. Jest to wielkość fizyczna odpowiadająca momentowi bezwładności w ruchu prostoliniowym.
Orbitalny moment pędu elektronu przybiera tyle wartości, ile wartości w danej powłoce może przyjąć poboczna liczba kwantowa, a to z kolei zależy od wartości głównej liczby kwantowej. W przypadku powłoki M, gdy n=3, orbitalny moment pędu może przybierać trzy wartości, ponieważ poboczna liczba kwantowa może wynosić 0, 1 lub 2.
Liczba podpowłok w danej powłoce jest równa wartości jej głównej liczby kwantowej. W powłoce K, gdy n=1, występuje jedna podpowłoka s; w powłoce L, gdy n=2, występują dwie podpowłoki, s i p; w powłoce M, gdy n=3 - trzy podpowłoki, s, p i d; zaś w powłoce N, gdy n=4 - cztery podpowłoki, s, p, d i f.
Magnetyczna liczba kwantowa
Magnetyczna liczba kwantowa o symbolu m (niekiedy ml) może przyjmować wartości całkowite od -l do +l włącznie z zerem. Począwszy od powłoki L liczba ta może przyjąć więcej niż jedną wartość: dla l=0 m=0, a dla l=1 m=-1,0,1.
Zbiór elektronów opisanych jednakowym zestawem liczb kwantowych n, l, m nazywa się poziomem orbitalnym.
Magnetyczna liczba kwantowa kwantuje orientację przestrzenną wektora orbitalnego momentu pędu elektronu. Moment pędu jest wielkością wektorową, czyli posiada nie tylko wartość, ale także kierunek i zwrot. Różne możliwe orientacje przestrzenne wektora orbitalnego momentu pędu elektronu ujawniają się po przyłożeniu zewnętrznego pola magnetycznego. Kwantowanie orientacji przestrzennej rozważanego wektora dotyczy właściwie wartości rzutu tego wektora na określony kierunek (na przykład na kierunek przyłożonego pola). Zatem magnetyczna liczba kwantowa kwantuje wartość rzutu wektora orbitalnego momentu pędu elektronu na dany kierunek.
Dla podpowłoki s (l=0) magnetyczna liczba kwantowa przyjmuje tylko jedną wartość m=0, a zatem istnieje w tym przypadku tylko jeden poziom orbitalny, także oznaczany s. Dla podpowłoki p (l=1) magnetyczna liczba kwantowa może przyjąć jedną z trzech wartości: -1, 0 lub +1, a każdej z nich odpowiada jeden poziom orbitalny: px, py lub pz. Wreszcie dla podpowłoki d (l=2) magnetyczna liczba kwantowa może przyjąć jedną z pięciu wartości: -2, -1, 0, +1 lub +2. Odpowiadają im poziomy orbitalne dxy, dyz, dxz, ![]()
i ![]()
.
Spinowa liczba kwantowa
Spinowa liczba kwantowa o symbolu s może przybrać tylko jedną wartość s=½.
Stany elektronu opisane jednakowym zestawem liczb kwantowych n, l, m, s noszą wspólną nazwę orbitalu.
Spinowa liczba kwantowa kwantuje spin elektronu, określany też jako wewnętrzny moment pędu. To drugie określenie jest o tyle mylące, że może kojarzyć się z ruchem obrotowym elektronu, podczas gdy elektron nie ma żadnej wewnętrznej struktury i nie można w żaden sposób określić, czy wiruje. Podobnie, obserwując stojącą w miejscu, dobrze wypolerowaną jednokolorową kulę bilardową nie możemy powiedzieć, czy się ona obraca, czy też jest nieruchoma.
Spin jest wielkością kwantowomechaniczną i nie ma odpowiednika w fizyce klasycznej. Stanowi - obok masy i ładunku - jeden z podstawowych parametrów opisujących cząstki elementarne. Nie jest to jednak pojęcie wzięte „z powietrza” - w spójnej teorii naukowej wszystkie elementy muszą mieć swoje uzasadnienie. Pojęcie spinu zostało wprowadzone w celu wyjaśnienia magnetycznych właściwości niektórych cząstek. Elektron na przykład jest dipolem magnetycznym i zachowuje się jak mikroskopowy magnes, czego bez użycia właściwości zwanego spinem wyjaśnić się nie da.
Ponieważ spinowa liczba kwantowa przyjmuje tylko jedną wartość, przy opisie stanu kwantowego można ją pominąć bez straty informacji.
Magnetyczna spinowa liczba kwantowa
Magnetyczna spinowa liczba kwantowa o symbolu ms może przybrać jedną z dwu wartości: -½ lub +½.
Ponieważ piąta liczba kwantowa przyjmuje tylko dwie wartości, każdy orbital obejmuje dwa stany kwantowe („mieści” dwa elektrony).
Magnetyczna spinowa liczba kwantowa określa orientację przestrzenną wektora spinu (czyli jest analogiczna do magnetycznej liczby kwantowej m, określającej orientację wektora orbitalnego momentu pędu).
Z uwagi na dwie dopuszczalne wartości magnetycznej spinowej liczby kwantowej, wektor spinu może ustawić się w polu magnetycznym tylko tak, by jego rzut przyjmował jedną z dwóch wartości (potocznie mówi się o zwrocie „w górę” i „w dół”).
Liczby kwantowe a postać orbitalu
Należy jednak podkreślić, że dokładne rozwiązanie równania Schrödingera jest możliwe wyłącznie dla układu jednoelektronowego (na przykład atomu wodoru, jonów He+, Li2+ itd.). W przypadku układów wieloelektronowych pojawiają się komplikujące sytuację oddziaływania między poszczególnymi elektronami, wskutek czego trzeba stosować w mechanice kwantowej pewne przybliżenia.
W przypadku, gdy rozważamy elektrony w atomie, rozwiązania równania Schrödingera będą nazywane orbitalami atomowymi. W celu lepszego wyobrażenia przestrzennej postaci orbitalu (czyli rozkładu prawdopodobieństwa) wprowadza się pojęcie obszaru orbitalnego.
Obszar orbitalny to część przestrzeni wokół jądra, na zewnątrz której gęstość ładunku jest zaniedbywalnie mała (mniejsza od założonej wartości granicznej), a jednocześnie niższa od gęstości ładunku wewnątrz owej części przestrzeni.
Obszar orbitalny jest często utożsamiany z orbitalem, należy jednak pamiętać, że orbital to określone rozwiązanie równania Schrödingera, natomiast obszar orbitalny jest definiowany w sposób umowny.
Rozwiązania równania Schrödingera składają się zwykle z części radialnej (określającej odległość elektronu od jądra) i kątowej, określającej kształt obszaru orbitalnego. Wyjątek stanowi pierwsza powłoka, gdyż dla n=1 istnieje tylko jedna funkcja falowa (orbital s), o idealnie kulistym kształcie. Jest to funkcja czysto radialna, gdyż odległość elektronu od jądra jest w niej jednakowa niezależnie od kierunku.
Postać obszaru orbitalnego zależy od trzech pierwszych liczb kwantowych:
Główna liczba kwantowa n decyduje o rozmiarach kształtu orbitalnego.
Poboczna liczba kwantowa l decyduje o kształcie obszaru orbitalnego.
Magnetyczna liczba kwantowa m decyduje o orientacji przestrzennej obszaru orbitalnego.
Wzrost głównej liczby kwantowej jest równoznaczny ze wzrostem promienia obszaru orbitalnego. Jak wiadomo, w pierwszej powłoce n=1, l=0 i jedynym orbitalem wchodzącym w skład tej powłoki jest kulisty orbital s. Jednak poboczna liczba kwantowa może przyjąć wartość 0 (odpowiadającą orbitalowi s) także na dalszych powłokach. Orbital typu s zyskuje zatem swoje odpowiedniki charakteryzujące się wyższą energią elektronu, istniejące na wyższych powłokach. Dlatego dla pełnego opisu orbitalu s należy podać przy nim także wartość głównej liczby kwantowej: 1s, 2s, 3s będą oznaczać orbitale s o coraz większym promieniu, należące do powłok K, L i M.
Na drugiej powłoce (i dalszych) poboczna liczba kwantowa może przyjąć także wartość 1, której odpowiada obszar orbitalny p w kształcie „obrotowej ósemki” (albo hantli). Taki kształt nie jest jednak idealnie symetryczny, powstaje więc konieczność określenia jego ułożenia w przestrzeni (w tym celu rozważa się atom umieszczony pośrodku trójwymiarowego układu kartezjańskiego). Tę informację niesie magnetyczna liczba kwantowa, która dla l=1 może przyjmować wartości -1, 0 i +1. Odpowiadają one ułożeniu „ósemki” wzdłuż osi X, Y lub Z układu kartezjańskiego, co daje orbitale px, py i pz. Podobnie, jak w przypadku orbitalu s, pełny opis orbitalu p wymaga podania głównej liczby kwantowej, określającej, do której powłoki orbital należy: 2px, 2py, 3px itd.
Ze wzrostem wartości l kształt obszaru orbitalnego komplikuje się. Począwszy od trzeciej powłoki poboczna liczba kwantowa może przyjąć wartość 2, odpowiadającą orbitalowi d o kształcie dwóch „obrotowych ósemek” skrzyżowanych pod kątem prostym. Orbitali tych jest pięć, ponieważ magnetyczna liczba kwantowa może dla l=2 przyjmować wartości -2, -1, 0, +1 i +2, co odpowiada orbitalom dxy, dyz, dxz, ![]()
i ![]()
. Trzy pierwsze z nich znajdują się w płaszczyźnie wyznaczonej przez odpowiednie osie, na przykład ramiona „podwójnej ósemki” orbitalu dxy znajdują się w płaszczyźnie XY, pomiędzy osiami X i Y. Ramiona orbitali ![]()
są położone wzdłuż osi X i Y, natomiast orbital ![]()
ma wyjątkowy kształt pojedynczej ósemki z prostopadłym do niej „obwarzankiem”, znajdującym się w miejscu przewężenia ósemki. Orbital ten jest w układzie kartezjańskim położony wzdłuż osi Z.
Orbitale przedstawione za pomocą powierzchni granicznych mają następującą postać:
Warto na koniec zauważyć, że używane powszechnie sformułowania, mówiące o elektronach obsadzających czy zajmujących orbitale lub elektronach zajmujących orbitale, stanowią pewne uproszczenie dydaktyczne. W rzeczywistości orbital nie jest czymś w rodzaju półki bibliotecznej, na której ustawiamy książki-elektrony; jest on „tylko” funkcją matematyczną opisującą stan elektronu w atomie, a nie obiektem czy miejscem istniejącym niezależnie od elektronu.
Struktura powłok elektronowych atomów wieloelektronowych - kolejność zabudowy poziomów energetycznych
Chemik wyposażony w opisany w poprzednich podrozdziałach aparat chemii kwantowej jest w stanie wreszcie przystąpić do zwięzłego opisywania stanu elektronów w atomach. Opisanie stanu elektronu w atomie wieloelektronowym wymaga podania wartości liczb kwantowych tego elektronu (wystarczą cztery: n, l, m i ms, ponieważ spinowa liczba kwantowa jest zawsze równa ½).
W ustalaniu kolejności obsadzenia powłok decydujący głos ma zasada minimum energii: układ fizyczny, jakim jest atom ze swymi elektronami, będzie dążyć do stanu, w którym jego energia będzie jak najmniejsza. W związku z tym elektrony będą obsadzać powłoki i orbitale poczynając od stanu o najniższej energii (gdyż niżej się już nie da), i będą to robić po kolei, bez pozostawiania pustych miejsc.
Zapis, przedstawiający poszczególne powłoki, podpowłoki i orbitale atomu, wraz z obsadzającymi je elektronami, nazywa się konfiguracją elektronową.
Wobec tego najprostszy atom, atom wodoru w podstawowym stanie energetycznym, można przedstawić następującą konfiguracją elektronową:
1H K1
Podanie symbolu i liczby atomowej pierwiastka ułatwia ustalenie liczby elektronów, które musimy „rozmieścić” na powłokach, aby konfiguracja była prawidłowa.
2He K2
Powłoka K mieści tylko dwa elektrony, zatem w atomach kolejnych pierwiastków elektrony zaczynają zapełniać powłokę L:
3Li K2 L1
4Be K2 L2
…
10Ne K2 L8
W atomie następnego pierwiastka rozpoczyna się obsadzanie powłoki M:
11Na K2 L8 M1
12Mg K2 L8 M2
Poniższy rysunek ilustruje radialny rozkład gęstości elektronowej w atomie argonu z zaznaczonymi poszczególnymi powłokami.
Czy jednak zapis powłokowy zapewnia wszystkie potrzebne informacje o elektronach? Z podrozdziału 1.11 wynika, że nie. Symbole powłok (K, L, M) informują nas bowiem jedynie o wartości głównej liczby kwantowej, nie mówiąc nic o pozostałych. Już w przypadku atomu helu otrzymujemy w ten sposób dwa pozornie jednakowe elektrony. Należy zatem w konfiguracji elektronowej przedstawić także symbol podpowłoki, a jeśli to konieczne, pokazać także, na jakich poziomach orbitalnych znajdują się poszczególne elektrony. W tym celu stosuje się zapis typu 3p4, w którym pierwsza liczba oznacza wartość głównej liczby kwantowej (numer powłoki), litera (p lub s, d, f) jest symbolem podpowłoki i umożliwia jednoznaczne określenie wartości pobocznej liczby kwantowej, zaś liczba w górnym indeksie stanowi liczbę elektronów na danej podpowłoce. Wobec czego konfiguracje pierwiastków będą przedstawiać się następująco:
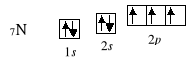
1H 1s1
2He 1s2
Obok reguły o minimum energii w mechanice kwantowej obowiązuje zasada, że poszczególne elektrony w atomie muszą różnić się wartością przynajmniej jednej opisującej je liczby kwantowej. Jest to tzw. zakaz Pauliego:
W danym atomie nie mogą istnieć elektrony opisane tymi samymi wartościami wszystkich liczb kwantowych.
W praktyce oznacza to, że jeśli elektrony znajdują się na tym samym poziomie orbitalnym, czyli są opisane jednakową wartością głównej, pobocznej i magnetycznej liczby kwantowej, to muszą różnić się wartością magnetycznej spinowej liczby kwantowej. Ta zaś ma tylko dwie dozwolone wartości, -½ i +½, więc poziom orbitalny mieści tylko dwa elektrony. Trzeci musi zacząć obsadzanie kolejnego poziomu, podpowłoki lub powłoki. Podpowłoka 1s obejmuje tylko jeden poziom orbitalny, więc kolejny elektron rozpoczyna obsadzanie podpowłoki 2s.
3Li 1s2 2s1
4Be 1s2 2s2
5B 1s2 2s2 2p1
10Ne 1s2 2s2 2p6
Analogicznie, podpowłoka p obejmuje trzy poziomy orbitalne, więc może maksymalnie pomieścić 3×2=6 elektronów. Kolejne elektrony rozpoczynają obsadzanie podpowłoki 3s i dalszych.
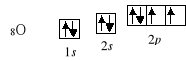
12Mg 1s2 2s2 2p6 3s2
16S 1s2 2s2 2p6 3s2 3p4
18Ar 1s2 2s2 2p6 3s2 3p6
Elektrony kolejnego pierwiastka teoretycznie powinny zacząć obsadzać podpowłokę 3d, tak się jednak nie dzieje, ponieważ niższą energię ma podpowłoka 4s.
20Ca 1s2 2s2 2p6 3s2 3p6 4s2
Dopiero teraz rozpoczyna się zapełnianie podpowłoki 3d:
21Sc 1s2 2s2 2p6 3s2 3p6 4s2 3d1
23V 1s2 2s2 2p6 3s2 3p6 4s2 3d3
33As 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p3
36Kr 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6
Od podanej wyżej kolejności obsadzania podpowłok istnieją pewne wyjątki, na przykład dla chromu i miedzi:
24Cr 1s2 2s2 2p6 3s2 3p6 4s1 3d5
29Cu 1s2 2s2 2p6 3s2 3p6 4s1 3d10
Przyczyna takich odstępstw zostanie wyjaśniona za chwilę, przy rozpatrywaniu obsadzenia poziomów orbitalnych.
Litania podpowłok zaczyna się wydłużać, a do końca układu okresowego jeszcze daleko. Cyrkon o liczbie atomowej 40 ma konfigurację elektronową:
40Zr 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d2
Zapis konfiguracji elektronowej pierwiastka można jednak skrócić, podając w nawiasie kwadratowym symbol pierwiastka, którego konfiguracja stanowi fragment konfiguracji zapisywanej, a potem resztę elektronów:
18Ar 1s2 2s2 2p6 3s2 3p6 ≡ [Ar]
20Ca [Ar] 4s2
21Sc [Ar] 4s2 3d1
33As [Ar] 4s2 3d10 4p3
Pierwiastek, który ma zastąpić część konfiguracji, wybiera się w oparciu o zapełnienie powłok. Hel ma zapełnioną całą pierwszą powłokę, a następny pierwiastek, lit, rozpoczyna zapełnianie powłoki drugiej. Argon ma zapełnione pierwsze trzy powłoki, a następny, potas, rozpoczyna zapełnianie powłoki czwartej. Podobna sytuacja występuje w przypadku neonu, kryptonu i pozostałych gazów szlachetnych - helowców. Ogólna zasada brzmi zatem:
Skrócony zapis konfiguracji elektronowej atomu pierwiastka polega na podaniu symbolu poprzedzającego go helowca oraz dopisaniu elektronów, nie występujących w atomie tegoż helowca.
Skrócony zapis konfiguracji elektronowej pozwala wysnuć dodatkowe ciekawe wnioski. Na przykład konfiguracje wapnia, skandu i wanadu różnią się jedynie liczbą elektronów po symbolu helowca (tu: argonu). Z drugiej strony konfiguracje elektronowe magnezu, wapnia i baru różnią się jedynie symbolem helowca, używanego dla skrócenia zapisu, natomiast liczba dopisywanych elektronów jest w przypadku wszystkich tych pierwiastków jednakowa. Można stąd wnosić, że o różnicach i podobieństwach we właściwościach chemicznych pierwiastków decyduje właśnie różna lub taka sama liczba elektronów.
Elektrony decydujące o właściwościach chemicznych pierwiastka znajdują się na ostatniej powłoce elektronowej atomu i nazywają elektronami walencyjnymi. Tylko te elektrony biorą udział w reakcjach chemicznych.
Najbardziej szczegółowy sposób przedstawienia konfiguracji elektronowej, prezentujący także rozmieszczenie elektronów na poziomach orbitalnych, polega na rysowaniu elektronów w kratkach wyobrażających poszczególne powłoki, podpowłoki i poziomy orbitalne. Podpowłoki s, p, d i f obejmują odpowiednio 1, 3, 5 i 7 poziomów orbitalnych, z których każdy przedstawiany jest w postaci jednej kratki o określonej wartości magnetycznej orbitalnej liczby kwantowej:
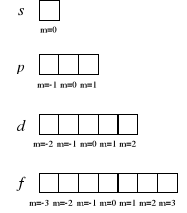
Elektrony są w tej metodzie przedstawiane jako pionowe strzałki o zwrocie w górę lub w dół, odpowiadającym zwrotowi wektora spinu, czyli odpowiednio dodatniej lub ujemnej wartości magnetycznej spinowej liczby kwantowej.
![]()
![]()
Zgodnie z zakazem Pauliego dwa elektrony obsadzające ten sam poziom orbitalny nie mogą mieć takiej samej wartości magnetycznej spinowej liczby kwantowej, czyli symbolizujące je strzałki muszą mieć przeciwny zwrot.
W analogiczny sposób przebiega zapełnianie podpowłoki/poziomu orbitalnego 2s w przypadku litu i berylu. Począwszy od boru elektrony zaczynają obsadzać podpowłokę 2p:
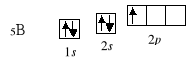
W tej sytuacji powstaje pytanie, gdzie powinien się znaleźć następny elektron? Jaka powinna być konfiguracja elektronowa następnego w kolejności atomu węgla? Nie jest to wcale problem akademicki - umieszczenie następnego elektronu na tym samym poziomie orbitalnym (w tej samej kratce) oznaczałoby, że atom węgla nie przejawiałby żadnych właściwości magnetycznych - byłby diamagnetykiem, natomiast umieszczenie elektronu na innym poziomie orbitalnym (powodujące obecność dwóch niesparowanych elektronów), pociągałoby za sobą paramagnetyzm tego atomu. Z pomocą przychodzi ponownie kryterium minimum energii, które mówi, że najkorzystniejszy energetycznie jest stan, w którym elektrony są maksymalnie „oddalone” od siebie, czyli w miarę możliwości zajmują odrębne poziomy orbitalne (potwierdzają to także właściwości magnetyczne atomu węgla). Szczegółowo rozwiązuje ten dylemat reguła Hunda:
W danej podpowłoce powinna istnieć możliwie jak największa liczba niesparowanych elektronów.
Niesparowane elektrony, obsadzające poziomy orbitalne tej samej podpowłoki, powinny mieć jednakową orientację spinu.
Do sparowania elektronów dochodzi dopiero po zajęciu wszystkich poziomów orbitalnych danej podpowłoki przez elektrony niesparowane.
Zgodnie z powyższymi zasadami konfigurację elektronową dalszych pierwiastków można przedstawić następująco:
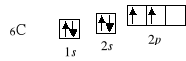
…
Począwszy od skandu, elektrony zaczynają obsadzać podpowłokę 3d. Podpowłoka d zapełnia się także zgodnie z regułą Hunda:

Następny w kolejności chrom powinien mieć konfigurację [Ar] 4s2 3d4, okazuje się jednak, iż różnica energii między poziomami 4s a 3d jest na tyle niewielka, że stanem korzystniejszym energetycznie jest umieszczenie pięciu elektronów na podpowłoce 3d. Zysk energetyczny, wynikający z utworzenia bardziej symetrycznego układu 4s1 3d5, z nawiązką wyrównuje nakład energii potrzebny do rozłączenia pary 4s2 i przeniesienia elektronu z podpowłoki 4s na 3d.

Konfiguracja d5 należy do szczególnie trwałych, podobnie jak konfiguracja d10, stąd kolejnym wyjątkiem jest miedź, charakteryzująca się konfiguracją [Ar] 4s1 3d10 zamiast [Ar] 4s2 3d9.
Zapis kratkowy umożliwia najdokładniejsze określenie wartości liczb kwantowych opisujących dany elektron. W poniższym przykładzie:
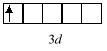
elektron znajduje się na trzeciej powłoce (n=3), podpowłoce d (l=2), poziomie orbitalnym o m=-2, a wartość jego magnetycznej spinowej liczby kwantowej wynosi +½ (liczba spinowa wynosi, jak zawsze, ½). Natomiast zapis typu 3d1 umożliwia odczytanie tylko dwóch pierwszych liczb kwantowych: n=3, l=2 (podpowłoka d).
Termy atomowe
Zapis konfiguracji elektronowej atomu, nawet w postaci kratkowej, nie zawiera jednak pełnej informacji na temat jego stanu energetycznego. W celu uzyskania takiej informacji należy uwzględnić fakt, że elektrony w atomie oddziałują między sobą, a ich wektory orbitalnych momentów pędu i spiny sumują się ze sobą. Dodawanie wektorów oczywiście nie jest prostą sprawą. Wektory należy składać, uwzględniając nie tylko ich wartości (długości), ale także orientację przestrzenną - kierunek i zwrot. Bezwzględną wartość wypadkowego wektora orbitalnego momentu pędu można obliczyć ze wzoru:
![]()
gdzie L to liczba kwantowa określona przez poboczne liczby kwantowe poszczególnych elektronów, np. l1 i l2. L przyjmuje wartości w zakresie l1+l2; l1+l2-1;... l1-l2. Jeśli rozważymy atom o konfiguracji ns2 np2, to L może być równe 2, 1 lub 0, przy czym skrajne wartości oznaczają odpowiednio antyrównoległą i równoległą orientację wektorów orbitalnego momentu pędu. Należy podkreślić, że w przypadku konfiguracji złożonych typu ns2 np2 całkowicie zapełnione podpowłoki, takie jak s2 czy p6, można pomijać w tego typu obliczeniach, ponieważ ich wypadkowy wkład jest zerowy.
Analogicznie składają się wektory spinu, a bezwzględną wartość wypadkowego wektora spinu oblicza się z podobnego wzoru:
![]()
W tym przypadku S jest spinową liczbą kwantową atomu, określoną przez spinowe liczby kwantowe poszczególnych elektronów. Ponieważ jednak wektor spinu ma znacznie bardziej ograniczone możliwości orientowania się w przestrzeni („w górę” lub „w dół”), dlatego możliwe wartości S stanowią jedynie zespół sum i różnic poszczególnych składników. W przypadku wspomnianego wcześniej pierwiastka o konfiguracji ns2 np2 S może wynosić ½+½=1 (spiny równoległe) albo ½-½=0 (spiny antyrównoległe).
Z uwagi na wzajemną zależność ruchów poszczególnych elektronów w atomie wieloelektronowym liczby kwantowe l i s tych elektronów nie mają takiego sensu fizycznego, jak w atomie jednoelektronowym. Służą jedynie do obliczania wartości L i S, i dopiero te liczby kwantowe, określające odpowiednio orbitalny i spinowy wypadkowy moment pędu atomu, opisują stan atomu (tzw. schemat Russella-Saundersa). Stany o różnych wartościach L i S różnią się energią z uwagi na odmienne orientacje wektorów orbitalnego momentu pędu i różny wkład energetyczny wynikając z odpychania się elektronów. Takie stany energetyczne atomu są nazywane termami atomowymi. Grupy termów o danej wartości L oznacza się odpowiednio:
Wartość L |
0 |
1 |
2 |
3 |
4 |
5 |
… |
Symbol termu |
S |
P |
D |
F |
G |
H |
… |
Oczywiście nie należy mylić liczby kwantowej wypadkowego spinu atomu S z termem S odpowiadającym minimalnej wartości wypadkowego orbitalnego momentu pędu.
Dodatkowy wpływ na energię atomu wywiera sprzężenie spinowo-orbitalne, polegające na wzajemnym oddziaływaniu orbitalnego i spinowego momentu magnetycznego. W efekcie uzyskujemy wektor pełnego momentu pędu:
![]()
którego wartość bezwzględną oblicza się z analogicznego wzoru, jak w przypadku L:
![]()
Liczba kwantowa pełnego momentu pędu J przyjmuje wartości z przedziału:
L+S, L+S-1, …, L-S (gdy L≥S)
Liczba możliwych wartości wektora pełnego momentu pędu wynosi 2S+1.
Sprzężenie spinowo orbitalne powoduje, że term rozszczepia się - staje się multipletem zawierającym 2S+1 poziomów o zbliżonej energii. Liczba 2S+1 to multipletowość termu.
Z powyższego rozumowania wynika, że danej konfiguracji atomu można przypisać kilka różnych stanów energetycznych, czyli kilka termów charakteryzujących różną wartością energii. Pełny symbol termu wymaga użycia wszystkich trzech liczba kwantowych atomu, tj. L, S i J:
![]()
Spróbujmy w takim razie ustalić term dla konfiguracji np2, czy raczej bardziej dokładnie dla ![]()
.
Zgodnie z przytoczonymi wcześniej wzorami L = 1 i S = 1. Multipletowość termu 2S+1=3. Zatem termem tej konfiguracji jest 3P, a J przyjmuje wartości 2, 1 i 0. Term jest zatem trypletem, składającym się ze stanów 3P2, 3P1, 3P0.
Dla niektórych konfiguracji może się zdarzyć, że wartość L będzie niższa od wartości S. Wtedy liczba J przyjmie wartości z przedziału:
S+L, S+L-1, …, S-L (gdy L<S)
W takim jednak przypadku multipletowość jest wielkością formalną, gdyż liczba składowych termu będzie odpowiadać 2L+1 (mniejszej od 2S+1).
Obliczmy termy atomowe dla wodoru i helu:
Parametr |
Wodór |
Hel |
Konfiguracja elektronowa |
1s1 |
1s2 |
Wartości L |
0 |
0 |
Symbol termu |
S |
S |
S |
½ |
0 |
Multipletowość (2S+1) |
2 |
1 |
Wartości J |
½ |
0 |
Pełne symbole termów |
2S1/2 (z uwagi na S>L multipletowość nie decyduje o liczbie termów) |
1S0 |
Warto zauważyć, że jak wspomniano wcześniej, wszystkie zapełnione podpowłoki (s2, p6, d10, f14) mogą być pomijane przy obliczeniach - nie wnoszą one wkładu ani do S, ani do L. Termem wszystkich pierwiastków o takich konfiguracjach jest 1S0; należą do tej grupy nie tylko gazy szlachetne, ale także berylowce (ns2), cynkowce ((n-1)d10 ns2), pallad (4s2 4p6 4d10), nobel (6s2 6p6 7s2).
Wodór i hel stanowią jednak proste przykłady z tylko jedną wartością L. Dla konfiguracji ns2 np2 ustaliliśmy wcześniej tryplet 3P2, 3P1, 3P0. Nie są to wszystkie możliwe termy takiej konfiguracji, ponieważ L może w jej przypadku przyjmować trzy wartości: 2, 1 i 0, odpowiadające symbolom D, P i S. Z kolei zwrot wektorów spinu elektronów p może być równoległy (S=1) lub antyrównoległy (S=0), co odpowiada multipletowości 3 lub 1. Pełny wykaz znajduje się w tabeli.
Nr |
ml |
L = Σ l |
S = Σ s |
Term |
||
|
1 |
0 |
-1 |
|
|
|
↑↓ |
|
|
2 |
0 |
1D |
|
↑ |
↑ |
|
1 |
1 |
3P |
|
↑ |
↓ |
|
1 |
0 |
1P |
|
↓ |
↑ |
|
1 |
0 |
1P |
|
↓ |
↓ |
|
1 |
-1 |
3P |
|
↑ |
|
↑ |
0 |
1 |
3S |
|
↑ |
|
↓ |
0 |
0 |
1S |
|
|
↑↓ |
|
0 |
0 |
1S |
|
↓ |
|
↑ |
0 |
0 |
1S |
|
↓ |
|
↓ |
0 |
-1 |
3S |
|
|
↑ |
↑ |
-1 |
1 |
3P |
|
|
↑ |
↓ |
-1 |
0 |
1P |
|
|
↓ |
↑ |
-1 |
0 |
1P |
|
|
↓ |
↓ |
-1 |
-1 |
3P |
|
|
|
↑↓ |
-2 |
0 |
1D |
|
Łatwo jednak zauważyć, że o ile wszystkie podane wyżej konfiguracje stosują się do zakazu Pauliego, o tyle część z nich nie spełnia reguły Hunda: 1, 8 i 15 w sposób oczywisty, a ponadto 3, 4, 7, 9, 12 i 13 - wszystkie o zerowym wypadkowym spinie. Właśnie reguła Hunda decyduje o wyborze termu podstawowego - stanu energetycznego odpowiadającego minimalnej energii. Stan (lokalnego) minimum energii jest bowiem stanem najtrwalszym.
Spośród termów o różnej multipletowości najniższej energii odpowiada term o najwyższej multipletowości. Oznacza to nie tylko, że elektrony powinny być maksymalnie „rozparowane”, ale również, że zwroty ich spinów powinny być zorientowane jednakowo, tylko wtedy bowiem uzyskamy maksymalną wypadkową wartość spinu (odpowiadającą maksymalnej multipletowości).
Spośród termów o danej multipletowości niżej energetyczny jest term o wyższej wartości liczby kwantowej L (czyli na przykład ze zbioru S, P, D - term D). Konsekwencją tej zasady jest fakt, że w zapisie konfiguracji kratkowej elektrony powinny wypełniać kratki po kolei od lewej lub od prawej (najpierw po jednym, a potem po drugim), bez pozostawiania luk - pustych kratek (orbitali).
Dla danych wartości S i L term o najniższej energii ma najniższą wartość J (L-S), gdy podpowłoka jest obsadzona mniej niż połową możliwych elektronów, a maksymalną wartość J (L+S) wtedy, gdy jest obsadzona co najmniej połową możliwych elektronów.
Zgodnie z powyższymi zasadami pełny symbol termu podstawowego pierwiastka o konfiguracji ns2 np2 (na przykład węgla) ma postać 3P0.
Biorąc pod uwagę zasady obsadzania orbitali i ustalania symboli termów, można zauważyć, że pewne konfiguracje elektronowe są „komplementarne” pod tym względem, że zawierają te same liczby niesparowanych elektronów i odpowiadają im te same wartości L. Jest tak nie tylko w przypadku konfiguracji s0 i s2 czy p0 i p6, ale także p1 i p5, p2 i p4, d1 i d9 itd. Z uwagi na zasadę nr 3 takie „komplementarne” konfiguracje będą mieć termy różniące się jedynie wartością J.
Konfiguracja elektronowa |
Term podstawowy (bez uwzględniania wartości J) |
s1 |
2S |
p1, p5 |
2P |
p2, p4 |
3P |
p3 |
4S |
d1, d9 |
2D |
d2, d8 |
3F |
d3, d7 |
4F |
d4, d6 |
5P |
d5 |
6S |
Warto zwrócić uwagę na fakt, że konfiguracjom charakteryzującym się połowicznym wypełnieniem podpowłoki, takim jak d5, odpowiada zawsze term typu S, podobnie jak podpowłokom pustym oraz całkowicie zapełnionym.
Układ okresowy. Periodyczność właściwości
Struktura układu okresowego
Tworząc swój układ okresowy, Dymitr Mendelejew opierał się na podobieństwie właściwości pierwiastków i - z małymi wyjątkami - rosnącej sekwencji ich mas atomowych. W ten sposób ułożył znane sobie pierwiastki w kolumny o zbliżonych właściwościach fizykochemicznych, a kolumny te ustawił według wzrostu mas, otrzymując tabelę złożoną z grup i okresów.
Lepsze poznanie struktury materii, a zwłaszcza budowy elektronowej atomów, umożliwiło bardziej dogłębne uzasadnienie kolejności pierwiastków w układzie okresowym. Podstawowymi kryteriami stały się w tym względzie całkowita liczba elektronów oraz liczba elektronów walencyjnych (czyli elektronów na ostatniej powłoce). Pierwiastki są w układzie okresowym ustawione w kolejności rosnącej całkowitej liczby elektronów, czyli wg liczby atomowej. Równocześnie są połączone w grupy (kolumny) obejmujące te pierwiastki, które zawierają jednakową liczbę elektronów walencyjnych na tych samych orbitalach (skand zawiera tyle samo elektronów, co gal, ale ma konfigurację 4s2 3d1, podczas gdy gal - 4s2 4p1). Dawniej używano też tzw. krótkiej tablicy Mendelejewa, zawierającej w jednej grupie oba zestawy pierwiastków o tej samej liczbie elektronów walencyjnych.
Liczba pierwiastków w okresie zależy od „pojemności elektronowej” danej powłoki. Pierwszy okres, w którym pierwiastki wypełniają powłokę K, mieszczącą dwa elektrony, liczy tylko dwa pierwiastki - wodór i hel. Drugi okres obejmuje osiem pierwiastków, gdyż powłoka L mieści osiem elektronów. Dalej sprawa zaczyna się komplikować. Teoretycznie kolejna powłoka mieści 18 elektronów, jednak po wypełnieniu podpowłoki s i p ośmioma elektronami (co ma miejsce w przypadku argonu) kolejny pierwiastek (19K) umieszcza 19. elektron na podpowłoce 4s, a nie 3d. Dzieje się tak wskutek kontrakcji powłok - rosnący ładunek jądra atomowego coraz silniej przyciąga otaczające je elektrony, lecz efekt ten zależy od symetrii orbitalu. Elektrony obsadzające podpowłokę d są przyciągane słabiej, niż elektrony z podpowłoki s. Dlatego w izolowanym atomie podpowłoka 4s ma niższą energię niż 3d i jej wypełnienie następuje wcześniej. Dopiero potem kolejny pierwiastek, skand, rozpoczyna wypełnianie podpowłoki 3d. Należy jednak już do czwartego okresu, gdyż wcześniejsze pierwiastki - potas i wapń - zaczęły wypełniać podpowłokę 4s, czyli zapoczątkowały kolejny okres. Analogiczne zjawisko ma miejsce w przypadku podpowłok 5s i 4d, 6s i 5d oraz 7s i 6d.
Wypełnienie w czwartym okresie podpowłok 4s, 3d i 4p (w takiej właśnie kolejności!) oznacza, że okres ten liczy 18 pierwiastków, bo tyle elektronów mieści się na tych trzech podpowłokach. Jednak czwarta powłoka teoretycznie obejmuje też podpowłoki 4d i 4f! Dlaczego nie zostają one wypełnione przez pierwiastki czwartego okresu? W przypadku podpowłoki 4d wyjaśnienie zostało już przytoczone - ma ona energię wyższą niż 5s i właśnie 5s zostanie wypełniona jako pierwsza. Jaka jest sytuacja w przypadku 4f? Ta podpowłoka ma energię wyższą nie tylko od 5s, ale także od 6s oraz - do pierwiastka 57 (La) - od 5d. W związku z tym kolejność wypełniania podpowłok jest następująca:
najpierw wypełniona zostanie podpowłoka 5s, co spowoduje zapoczątkowanie nowego, 5. okresu (rubid i stront);
potem elektrony obsadzają podpowłokę 4d, która ma niższą energię od 5p;
potem wypełniona zostaje podpowłoka 5p i na tym 5. okres się kończy, ponieważ podpowłoki 5d, 4f i 5f mają energię wyższą od 6s;
kolejne pierwiastki wypełniają zatem podpowłokę 6s (cez i bar), zapoczątkowując kolejny okres;
następnie rozpoczyna się wypełnianie podpowłoki 5d, ale po obsadzeniu jej jednym elektronem (lantan), w przypadku kolejnego pierwiastka (ceru) niższa staje się energia podpowłoki 4f i na niej lokuje się nie tylko kolejny elektron, ale i ten, który w przypadku lantanu znajduje się na podpowłoce 5d.
Niewielkie różnice energii między poszczególnymi poziomami w dalszych okresach powoduje, że poziomy energetyczne mogą się nakładać na siebie. W takim przypadku kolejność energetyczną poszczególnych powłok i podpowłok ustala się nie na podstawie najniższej wartości liczby n, ale sumy n+l - jest to zasada Kleczkowskiego. W tej interpretacji dla podpowłoki 4s otrzymujemy wartość 4+0=4, natomiast dla 3d 3+2=5, więc niższą energię ma podpowłoka 4s. Dopiero gdy suma n+l jest jednakowa, o kolejności decyduje wartość n - im niższa, tym niższa energia podpowłoki.
W związku z opisaną wyżej kolejnością obsadzania orbitali elektronowych układ okresowy dzieli się na okresy i grupy. Liczy siedem okresów, z których 1. zawiera dwa pierwiastki, 2. i 3. - po osiem, 4. i 5. - po osiemnaście, a 6. i 7. - po 32 (w siódmym okresie istnienie niektórych pierwiastków nie zostało jeszcze ostatecznie potwierdzone, zresztą część z nich otrzymano w znikomych ilościach po kilka atomów).
W zależności od tego, którą podpowłokę obsadzają w związkach chemicznych elektrony walencyjne pierwiastka, układ okresowy dzieli się na cztery bloki: s, p d i f. Grup w układzie okresowym znajduje się 18, przy czym im dalsza powłoka jest obsadzana elektronami, tym mniejsze różnice właściwości między pierwiastkami. Poszczególne lantanowce i aktynowce różnią się między sobą tak niewiele, że zamiast tworzyć dla nich 14 dodatkowych grup, ujmuje się te pierwiastki jako dwie „grupy poziome”. Pozostałe grupy - kolumny układu okresowego - ponumerowane są cyframi arabskimi od 1 do 18. Liczba elektronów walencyjnych pierwiastka jest grupach 1÷12 równa numerowi grupy, a w grupach 13÷18 - numerowi grupy pomniejszonemu o 10; liczba ta określa równocześnie maksymalny stopień utlenienia.
Maksymalna wartościowość pierwiastka zależy od liczby orbitali walencyjnych. Pojęcie tych orbitali definiuje się analogicznie, jak elektronów walencyjnych - są to orbitale ostatniej powłoki. W takiej sytuacji pierwiastki 1. okresu są maksymalnie 1-wartościowe (1s), drugiego okresu - maksymalnie 4-wartościowe (2s, 2px, 2py, 2pz), trzeciego - maksymalnie 9-wartościowe (3s, 3px, 3py, 3pz, 3dxy, 3dxz, 3dyz, 3dx2-y2, 3dz2). Teoretyczna maksymalna wartościowość w przypadku pierwiastków dalszych okresów przekracza 9, jednak w praktyce wartościowości wyższe od 9 pojawiają się bardzo rzadko - w przypadku pierwiastków bloku f.
Wykorzystanie elektronów walencyjnych i atomowych orbitali walencyjnych do tworzenia wiązań wiąże się z pojęciami wysycenia walencyjnego i koordynacyjnego. Wysycenie walencyjne oznacza wykorzystanie przez atom wszystkich elektronów walencyjnych do tworzenia wiązań, a wysycenie koordynacyjne - wykorzystanie do tworzenia wiązań wszystkich atomowych orbitali walencyjnych. Wysycenie to można stopniować w zależności od tego, jakie wiązania zostały utworzone z orbitali i elektronów walencyjnych. Atom, który zużył wszystkie elektrony/orbitale walencyjne do tworzenia samych wiązań σ jest bardziej wysycony niż taki, który utworzył oprócz wiązań σ także π.
Periodyczność właściwości fizykochemicznych pierwiastków
Właściwości fizykochemiczne pierwiastków zależą rzecz jasna od budowy ich atomów, a ściślej - od budowy powłok elektronowych, ponieważ to elektrony uczestniczą w procesach fizycznych, takich jak wzbudzenie czy jonizacja, oraz w reakcjach chemicznych (wyłącznie elektrony walencyjne). W takiej sytuacji periodyczność właściwości fizykochemicznych pierwiastków wynika w prosty sposób z faktu, że kolejne elektrony obsadzają w określonych odstępach między pierwiastkami analogiczne podpowłoki (na przykład 2s, 3s, 4s, 5s itd.) kolejnych powłok, w związku z czym można w układzie okresowym wyróżnić grupy pierwiastków o analogicznych konfiguracjach elektronowych i jednakowych liczbach elektronów walencyjnych. Sposób obsadzenia podpowłok decyduje więc o właściwościach fizycznych i chemicznych poszczególnych pierwiastków.
Ze wzrostem liczby atomowej pierwiastki zawierają coraz więcej cząstek w jądrze atomowym i coraz więcej elektronów wokół niego. O ile rozmiar jądra atomowego nie odgrywa żadnej roli dla chemika, a masa atomowa - dość ograniczoną, o tyle rozmiar atomu wyznaczony przez jego elektrony oraz liczba tych elektronów mają znaczenie zasadnicze. Spójrzmy jeszcze raz na radialny rozkład gęstości elektronowej, tym razem w atomie sodu:
Stan (położenie) elektronu w atomie jest określony przez funkcję falową, czyli w kategorii prawdopodobieństwa. Dlatego nie można w sposób całkowicie ścisły zmierzyć wielkości atomu, a promień atomowy należy zdefiniować w podobny sposób, jak definiuje się powierzchnie graniczne. Na powyższym wykresie nie ma ostrych, liniowych „pików”, odpowiadających ściśle określonym wartościom promienia atomowego. Jako promień swobodnego atomu można przyjąć teoretyczne położenie maksimum gęstości ładunku najbardziej zewnętrznej obsadzonej podpowłoki elektronowej, czyli 3s w przypadku sodu - jest to promień orbitalny.
W praktyce jednak atomy nie występują jako swobodne, chyba że w bardzo wysokiej próżni. Chemik ma do czynienia z atomami związanymi, czy to w cząsteczkach, czy w sieci krystalicznej, czy też - w przypadku helowców - pojedynczych atomów, które jednak nie są całkowicie niezależne. Dlatego praktyczne znaczenie mają tylko promienie efektywne. Jednak wielkość efektywnego promienia atomu zależy od natury oddziaływań między atomami; zasadniczo istotne są promienie w przypadku oddziaływań jonowych i kowalencyjnych (pozostałe rodzaje wiązań stanowią w mniejszym lub większym stopniu ich modyfikacje). Definiuje się zatem - i mierzy - promienie kowalencyjne (określane też po prostu jako promienie atomowe) i jonowe.
W miarę wzrostu liczby atomowej, a zatem i liczby elektronów w atomie, rośnie elektrostatyczne odpychanie między nimi, czego przejawem jest obsadzanie orbitali o coraz wyższych wartościach ml i l. Równocześnie jednak rośnie ładunek jądra, które przyciąga elektrony coraz silniej, dlatego w danym okresie promień atomu maleje w prawo (ze wzrostem Z). Jest to spowodowane również tym, że w konfiguracjach elektronowych pojawiają się zamknięte powłoki s2, p6 i d10, a zamknięte powłoki są zawsze szczególnie zwarte. Dlatego, jak widać na wykresie zależności promienia orbitalnego od liczby atomowej, małymi rozmiarami wyróżniają się atomy o całkowicie zapełnionych powłokach (helowce), a także o zamkniętych podpowłokach (cynkowce, (n-1)d10 ns2).
Z drugiej strony, rosnąca liczba podpowłok powoduje wzrost rozmiarów atomu, dlatego promień atomu (na ogół) rośnie w dół grupy (ze wzrostem Z). W rezultacie największy promień atomowy mają cez i frans (lewy dolny narożnik układu), a najmniejszy - hel i neon (prawy górny).
Wszystkie pozostałe właściwości pierwiastków w mniej lub bardziej bezpośredni sposób zależą właśnie od promienia atomowego.
Chemiczną naturę pierwiastka determinuje zdolność jego atomów do przyłączania lub oddawania elektronów, a tę z kolei określają takie parametry, jak powinowactwo do elektronu i elektroujemność z jednej strony oraz energia (potencjał) jonizacji z drugiej.
Energia (potencjał) jonizacji to energia potrzebna do „wyrwania” elektronu z atomu; często jest ona wyrażana przez napięcie, jakie jest potrzebne do wyrwania elektronu, stąd określa się ją też jako potencjał jonizacji i wyraża w elektronowoltach. Energia jonizacji zależy głównie od efektywnego ładunku jądra, radialnej odległości elektronu od jądra (czyli wartości promienia orbitalnego) oraz głębokości przenikania zewnętrznego elektronu do wewnętrznych powłok, która maleje w kolejności s>p>d>f. W związku z tym wartość energii jonizacji rośnie w okresach w prawo, zgodnie ze wzrostem ładunku jądra, a w grupach maleje ze wzrostem Z (ponieważ ze wzrostem Z rośnie promień atomowy). W rezultacie najwyższą energią jonizacji charakteryzuje się hel, a najniższą - cez i frans.

Jak widać na powyższym wykresie, najwyższą energią pierwszej jonizacji charakteryzują się atomy o całkowicie zapełnionych powłokach - helowce (wyróżniają się też pod tym względem cynkowce o konfiguracji (n-1)d10 ns2, zwłaszcza rtęć). Najniższą energię pierwszej jonizacji mają atomy zawierające tylko jeden elektron walencyjny - litowce (wodór jest oczywiście wyjątkiem).
Wartość energii jonizacji określa skłonność atomu do tworzenia kationu, a zatem decyduje o zdolnościach redukujących pierwiastków.
Energia powinowactwa elektronowego to efekt energetyczny procesu przyłączenia elektronu do obojętnego atomu, czyli utworzenia jednoujemnego anionu (zarówno atom, jak i anion muszą występować w stanie podstawowym). Na ogół energia powinowactwa elektronowego jest liczbowo równa energii jonizacji, ponieważ elektron przyłączany do atomu lokuje się na tym niezapełnionym orbitalu walencyjnym, co w większości pierwiastków oznacza ten sam orbital, z którego elektron jest usuwany w trakcie jonizacji. Reguły tej nie spełniają pierwiastki, których obojętne atomy w stanie podstawowym mają powłoki lub podpowłoki całkowicie zapełnione (helowce, berylowce) lub połowicznie (azotowce). Takie konfiguracje elektronowe są szczególnie trwałe i mogą wymagać umieszczenia elektronu na następnym, wyższym poziomie energetycznym. Dlatego proces tworzenia jednoujemnego anionu jest w przypadku np. berylowców procesem endoergicznym. Przyłączenie do atomu więcej niż jednego elektronu nie jest możliwe również z powodów energetycznych, dlatego wieloujemne jony typu O2-, N3- nie istnieją w stanie wolnym.
Proces tworzenia anionu jest więc na ogół procesem egzoergicznym, w przeciwieństwie do jonizacji, która jest zawsze endoergiczna.
Skłonność do tworzenia anionów rośnie w okresach w prawo, aczkolwiek niejednostajnie - litowce i borowce mają wyższą energię powinowactwa elektronowego niż berylowce. Skłonność ta maleje ponadto w dół grup, aczkolwiek i tu istnieją wyjątki. Wskutek słabszego odpychania elektronów atom chloru (o większych rozmiarach) ma wyższe powinowactwo elektronowe od atomu fluoru (jest silniejszym utleniaczem).
Energia powinowactwa elektronowego, jako przejaw skłonności do atomu do przyjmowania elektronu, określa też zdolności utleniające pierwiastków.
Poniższy rysunek dotyczy pierwiastków bloku p z wyłączeniem helowców.

Elektroujemność charakteryzuje względną zdolność danego atomu do uzyskiwania ładunku ujemnego w wyniku ściągnięcia na siebie gęstości elektronowej. Właściwość ta określa polaryzację elektryczną atomu danego pierwiastka w danym związku (to, czy przyjmuje on dodatni, czy ujemny stopień utlenienia). Stan polaryzacji elektrycznej atomu w związku zawsze zależy co najmniej od rodzaju drugiego atomu, z którym pierwszy tworzy wiązanie, może się więc zdarzyć, że ten sam pierwiastek będzie spolaryzowany dodatnio w związkach z pierwiastkami o wyższej elektroujemności, a ujemnie - w związkach z pierwiastkami o niższej elektroujemności. Np. wodór (2,1) w wiązaniu z tlenem (3,5) jest zawsze spolaryzowany dodatnio, a w związkach z litowcami (elektroujemność ≤ 1,0) - ujemnie.
W przypadku, gdy różnica elektroujemności jest niewielka lub zerowa, w celu ustalenia znaku polaryzacji elektrycznej atomu trzeba uciec się do rozważenia także innych czynników. Przyjmuje się np., że węgiel w węglowodorach jest spolaryzowany ujemnie, a wodór dodatnio, co znajduje potwierdzenie w odporności tych związków na hydrolizę. Takie polaryzacje można np. tłumaczyć większym ładunkiem jądra atomowego węgla niż wodoru, co powoduje silniejsze przyciąganie elektronów przez węgiel.
Elektroujemność jest obliczana teoretycznie, a metodyka tych obliczeń może być różna, dlatego istnieje wiele skal elektroujemności, z których najpopularniejsze są obecnie skale Paulinga i Allreda-Rachowa.

Jak widać na powyższym rysunku (nie uwzględniającym helowców!), elektroujemność rośnie w okresach w prawo, a w grupach maleje ze wzrostem liczby atomowej. W związku z tym najwyższą elektroujemnością (niezależnie od skali!) charakteryzuje się fluor, a najniższą - cez.
Podsumowując, o zmianach parametrów atomów można powiedzieć, że:
Z lewa na prawo:
promień atomowy maleje,
energia jonizacji rośnie,
elektroujemność rośnie.
Z góry na dół:
promień atomowy rośnie,
energia jonizacji maleje,
elektroujemność maleje.
W ramach ciekawostki warto zaprezentować też periodyczność rozpowszechnienia pierwiastków we Wszechświecie w zależności od liczby atomowej. W większych ilościach występują pierwiastki o parzystych Z (linia ciągła) niż o nieparzystych (linia przerywana). Wyjątkiem jest wodór, który, jak już wspomnieliśmy, powstał w największej obfitości w początkowej fazie istnienia Wszechświata. Pozostałe pierwiastki, które wyróżniają się na tym wykresie, to te, które mają najbardziej rozpowszechnione izotopy o jądrach parzysto-parzystych: ![]()
; oraz żelazo, którego jądro atomowe jest szczególnie trwałe i stanowi końcowy etap przemian termojądrowych, zachodzących we wnętrzach gwiazd zbyt małych, by wybuchnąć jako supernowe.
Typy wiązań i kryształów oraz ich wpływ na właściwości substancji
Wiązania chemiczne
Wiązanie chemiczne jest tym, co łączy atomy we wszelkiego rodzaju strukturach złożonych, począwszy od cząsteczek dwuatomowych. Rozróżnia się kilka rodzajów wiązań, wszystkie jednak mają w zasadzie naturę elektrostatyczną - są tworzone przez elektrony, których maksimum gęstości prawdopodobieństwa przypada na fragment przestrzeni między łączonymi atomami. Innymi słowy, ujemne elektrony są siłą spajającą ze sobą dodatnie jądra atomowe.
Wiązanie chemiczne może powstać tylko wtedy, kiedy towarzyszy mu wydzielenie energii. O ile tworzenie wiązania jest zawsze procesem egzoergicznym, o tyle należy pamiętać, że większość reakcji chemicznych jest związana nie tylko z tworzeniem wiązań, ale i rozerwaniem wcześniej istniejących (w cząsteczkach pierwiastków lub ich sieci krystalicznej). Dlatego nie wszystkie reakcje chemiczne są egzoergiczne i nie wszystkie zachodzą samorzutnie. Jednak spora część reakcji endoergicznych zachodzi w przyrodzie samorzutnie dzięki czynnikowi entropowemu (towarzyszy im wzrost entropii) albo dzięki zmianom warunków zewnętrznych (ciśnienia i temperatury), którym mogą też towarzyszyć zmiany efektu energetycznego reakcji.
Wiązania chemiczne można klasyfikować wg różnych kryteriów.
Kryterium |
Klasyfikacja |
|
Liczba atomów |
Obejmuje dwa atomy - wiązanie zlokalizowane (dwucentrowe) |
Obejmuje więcej niż dwa atomy - wiązanie zdelokalizowane (wielocentrowe) |
Krotność wiązania |
Pojedyncze - obejmuje tylko wiązanie σ |
Wielokrotne - oprócz wiązania σ zawiera też:
|
Zależność siły wiązania od kierunku pomiaru |
Zależy - wiązanie kierunkowe |
Nie zależy - wiązanie bezkierunkowe |
Pochodzenie elektronów tworzących wiązanie |
Po jednym od każdego atomu |
Pierwszy atom (donor) wnosi parę elektronową, a drugi (akceptor) przyjmuje ją na wolny orbital - wiązanie donorowo-akceptorowe |
Wysycenie elektronami |
Wszystkie wiążące orbitale molekularne wypełnione elektronami - wiązanie wysycone |
Nie wszystkie wiążące orbitale molekularne wypełnione elektronami - wiązanie niewysycone |
Wiązanie donorowo-akceptorowe bywa też nazywane koordynacyjnym, gdyż jest szczególnie charakterystyczne dla metali bloku d i f, których połączenia stanowią większość związków koordynacyjnych. Szczególny przypadek takiego wiązania stanowi wiązanie wodorowe, w którym atom wodoru o dodatniej polaryzacji (np. stanowiący dodatni biegun dipola), połączony wysoce polarnym wiązaniem z atomem o wysokiej elektroujemności, jest akceptorem pary elektronowej innego atomu o wysokiej elektroujemności.
Ponadto wiązania klasyfikuje się pod względem symetrii i pod względem charakteru, który zależy od wielu czynników: ładunku jąder atomowych, konfiguracji elektronowych atomów, promieni atomowych. Pod względem charakteru można wyróżnić trzy zasadnicze typy wiązania - kowalencyjne, jonowe i metaliczne. Jako przybliżoną zasadę można podać, że pierwiastki o wysokiej elektroujemności tworzą wiązania kowalencyjne, a o niskiej elektroujemności - metaliczne. W przypadku, gdy wiązanie tworzą dwa różne atomy, o jego naturze decyduje różnica elektroujemności obu pierwiastków. Przy dużej różnicy elektroujemności powstaje wiązanie jonowe, a przy niewielkiej - kowalencyjne spolaryzowane.
Najważniejsze parametry opisujące wiązanie to:
długość wiązania, mierzona na przykład za pomocą metod analizy rentgenostrukturalnej, jest miarą siły wiązania i pozwala pośrednio wnioskować o krotności lub rzędzie wiązania;
krotność wiązania - opisuje wiązania zlokalizowane i informuje o „składzie” wiązania, tj. czy na dane wiązanie składa się tylko wiązanie σ, czy także π i δ;
rząd wiązania - opisuje przede wszystkim systemy z wiązaniami zdelokalizowanymi, czyli układy wielocentrowe.
Rząd wiązania (rw) oblicza się ze wzoru:
![]()
gdzie nw - liczba elektronów wiążących, na - liczba elektronów antywiążących, LK - liczba koordynacji (liczba atomów bezpośrednio połączonych z danym atomem). Obie liczby elektronów najpewniej ustala się, rysując diagram orbitali molekularnych dla danej cząsteczki (o czym będziemy mówić na kolejnych wykładach). Istnieją jednak pewne przybliżone sposoby ustalania tych parametrów; na przykład w większości związków pierwiastków bloku p elektrony antywiążące nie występują i można obliczać rząd wiązania po prostu na podstawie wartościowości:
![]()
gdzie w liczniku występuje suma liczby poszczególnych rodzajów wiązań (σ, π i δ).
Obliczmy dla przykładu rząd wiązania w jonie siarczanowym(VI), który zawiera zdelokalizowane wiązanie π. W celu ustalenia liczby poszczególnych wiązań najlepiej wyjść ze wzoru strukturalnego (kreskowego) cząsteczki odpowiedniego kwasu; widać z niego, że siarka w H2SO4 tworzy cztery wiązania σ i dwa π (czyli jest sześciowartościowa). Liczba koordynacji siarki w jonie SO42- wynosi cztery, więc rw = 6/4 = 1½. W przeciwieństwie do wartościowości i krotności wiązania rw może przyjmować wartości ułamkowe - taka wartość świadczy o istnieniu wiązań zdelokalizowanych.
Wartość rzędu wiązania niższa od 1 świadczy o istnieniu słabych, zdelokalizowanych wiązań σ; związki tego typu są mało trwałe. Wartość rw równa 1 oznacza występowanie w związku wyłącznie wiązań σ. Rząd wiązania wyższy od 1 informuje o istnieniu także wiązań π (ewentualnie δ).
Wiązania w ujęciu mechaniki kwantowej
Kwantowomechaniczny opis budowy cząsteczki wykonywany jest analogicznie, jak opis budowy atomu wieloelektronowego. W większości cząsteczek (poza H2+) występuje bowiem więcej niż jeden elektron, co wymusza uwzględnienie elektrostatycznego odpychania między elektronami, a dodatkowo pojawia się też elektrostatyczne odpychanie między jądrami atomowymi.
Przed przystąpieniem do rozwiązania równania Schrødingera dla cząsteczki przyjmuje się tzw. zasadę Borna-Oppenheimera. Mówiąc w uproszczeniu, zasada ta uwzględnia fakt, że jądra atomowe mają masy od kilku do kilkuset tysięcy razy większe niż masa elektronu, wobec czego o wiele większa jest ich bezwładność. Drgania jąder atomowych w cząsteczce zachodzą stosunkowo wolno w porównaniu z ruchem elektronów, w związku z czym nie wpływają na stany elektronowe cząsteczek.
Uwzględnienie wszystkich oddziaływań, zwłaszcza międzyelektronowych, występujących w cząsteczce wieloelektronowej, jest trudne. Dlatego, podobnie jak w przypadku atomów, równanie Schrødingera można w sposób dokładny rozwiązać jedynie dla jonu H2+ (zawierającego tylko jeden elektron). W przypadku wszystkich pozostałych cząsteczek konieczne jest stosowanie przybliżeń, co czyni się w ramach formalizmów teorii zaburzeń i metody wariacyjnej.
W rezultacie otrzymujemy zestaw funkcji będących rozwiązaniami równania Schrødingera dla cząsteczki - czyli zestaw orbitali molekularnych. Dokładniejszy opis tego procesu i uzyskiwanych dzięki niemu wyników znajdzie się w wykładzie o teorii orbitali molekularnych (MO). Drugą podstawową teorią budowy cząsteczek jest teoria wiązań walencyjnych (VB).
Wiązanie a jego symetria
Symetria rozkładu gęstości ładunku/prawdopodobieństwa umożliwia sklasyfikowanie wiązań na σ, π i δ. Mówiąc ściślej, wiązania klasyfikuje się w ten sposób na podstawie pobocznej liczby kwantowej odpowiednich orbitali molekularnych, która decyduje o rozkładzie przestrzennym gęstości prawdopodobieństwa znalezienia elektronu.
Wartość l |
0 |
1 |
2 |
3 |
AO |
s |
p |
d |
f |
MO |
σ |
π |
δ |
… |
Orbitale molekularne, podobnie jak orbitale atomowe, można przedstawić w postaci powierzchni granicznych. W przypadku AO s nie obserwujemy żadnych płaszczyzn węzłowych. Orbitale p mają jedną płaszczyznę węzłową, d - dwie, a f - trzy (co najlepiej widać na płaskich rzutach konturów orbitali:
Analogiczne rozumowanie można przeprowadzić w odniesieniu do MO. Orbital (wiązanie) σ nie ma płaszczyzn węzłowych zawierających oś wiązania, orbital π ma jedną płaszczyznę węzłową, a δ - dwie.
Z powyższego zastrzeżenia co do położenia płaszczyzny węzłowej wynika, że można konstruować orbitale molekularne z takich AO, których płaszczyzny węzłowe nie będą zawierały osi wiązania. W związku z tym MO σ może powstać również z kombinacji orbitali p lub d, a nawet s z p i s z d.
Porównując powyższe rysunki można zauważyć, że w przypadku wiązania σ (zwłaszcza σss) największa część gęstości prawdopodobieństwa znalezienia elektronu znajduje się pomiędzy atomami tworzącymi wiązanie. Efekt wiążący jest więc tu najsilniejszy i wiązanie σ jest najmocniejsze. Jest to podstawowy rodzaj wiązania, który poza nielicznymi wyjątkami zawsze powstaje podczas tworzenia cząsteczki jako pierwszy. Następnie między dwoma danymi atomami mogą ewentualnie powstać dwa wiązania π, a na koniec wiązanie δ.
Jeśli założymy, że oś cząsteczki jest osią Z układu kartezjańskiego, wówczas wiązanie σ może powstać w pierwszej kolejności z orbitali s, następnie z orbitali pz, a wreszcie z orbitali dz2. Wiązanie σ zajmuje przestrzeń bezpośrednio między atomami, „blokując ją” dla innych wiązań. Zatem między dwoma danymi atomami zawsze powstaje tylko jedno wiązanie σ z tych orbitali, które są dostępne.
Wiązanie π (charakteryzujące się jedną płaszczyzną węzłową w osi wiązania) może powstać z orbitali, które mają jedną płaszczyznę węzłową zawierającą oś wiązania. Należą do nich przy takim ułożeniu cząsteczki orbitale px i py oraz dxz i dyz. Widać z tego, że w cząsteczce dwuatomowej mogą powstać dwa wiązania π, których maksima rozkładu gęstości elektronowej będą znajdować się „nad i pod” oraz „po bokach” osi wiązania. Jak w przypadku wiązań σ, powstanie określonych orbitali molekularnych π blokuje daną część przestrzeni dla innych wiązań, w związku z czym jeśli w cząsteczce istnieje już wiązanie π utworzone z orbitali px, orbitale dxz nie mogą utworzyć kolejnego wiązania π. Trzeba jednak zauważyć, że w wiązaniach π maksima rozkładu gęstości prawdopodobieństwa nie znajdują się bezpośrednio między atomami, czyli elektrony π rzadziej przebywają w tym obszarze i ich wpływ wiążący jest mniejszy niż wpływ elektronów σ. Oznacza to, że wiązanie π jest słabsze od wiązania σ.
Rozkłady gęstości prawdopodobieństwa obu wiązań π są względem siebie położone pod kątem prostym (podobnie jak orbitale px i py oraz dxz i dyz). W cząsteczce pozostaje jeszcze miejsce „pomiędzy” wiązaniami π. Czy istnieją jakieś orbitale atomowe, które mogłyby utworzyć wiązanie w tym miejscu? Okazuje się, że tak - orbital dxy leży między osiami X i Y (orbitale px i py oraz dxz i dyz - na tych osiach). Obie jego płaszczyzny węzłowe będą zawierać oś cząsteczki (sam orbital jest do niej prostopadły). Powstanie zatem wiązanie (MO), którego powierzchnie graniczne będą zawierać dwie płaszczyzny węzłowe - dlatego nie będzie to orbital typu π, tylko typu δ. Elektrony tworzące wiązanie typu δ przebywają jeszcze dalej od osi wiązania niż elektrony π, co oznacza, że wiązanie δ jest słabsze zarówno od σ, jak i π.
Teoretycznie możliwe jest też powstanie drugiego wiązania typu δ, ponieważ istnieje jeszcze jeden AO prostopadły do osi wiązania, którego obie płaszczyzny węzłowe będą zawierać tę oś - orbital dx2-y2. Powstanie takiego wiązania jest jednak nieco utrudnione, ponieważ jego maksimum rozkładu gęstości prawdopodobieństwa częściowo nakładałoby się na maksima odpowiadające wiązaniom π. Jak dotąd nie znaleziono przekonywujących dowodów na istnienie wiązania pięciokrotnego, czyli zawierającego oba wiązania δ.
Wiązanie |
Skład wiązania |
Wzrost długości wiązania |
Wzrost siły wiązania |
Pojedyncze |
σ |
|
|
Podwójne |
σ + π |
|
|
Potrójne |
σ + π + π |
|
|
Poczwórne |
σ + π + π + δ |
|
|
Należy podkreślić, że fakt, iż np. wiązanie π jest słabsze od wiązania σ, nie oznacza, że wiązanie podwójne jest słabsze od pojedynczego! Siła całego wiązania jest w przybliżeniu sumą siły wiązań poszczególnych komponentów σ, π i δ. Im silniejsze wiązanie, tym większe zbliżenie atomów powoduje, więc długość wiązania jest odwrotnie proporcjonalna do jego siły. Miarą siły wiązania jest energia wiązania (energia, jaką trzeba dostarczyć do jego zerwania, lub energia, jaka wydziela się w trakcie powstawania wiązania).
Wiązanie a jego charakter
Jak wspomniano wcześniej, trzema zasadniczymi typami wiązań są kowalencyjne, jonowe i metaliczne. Pozostałe typy wiązań, jakie czasami się wyróżnia, są podtypami jednego z tych trzech. Wiązanie donorowo-akceptorowe jest w rzeczywistości podtypem wiązania kowalencyjnego spolaryzowanego, zaś wiązanie wodorowe również powstaje w mechanizmie donorowo-akceptorowym.
Wiązanie kowalencyjne i kowalencyjne spolaryzowane
Wiązanie kowalencyjne powstaje w przypadku, gdy różnica elektroujemności obu łączących się atomów jest na tyle niewielka (albo zerowa), że elektrony tworzące wiązanie znajdują się pod wpływem obu jąder atomowych.
Pierwszym skrajnym przypadkiem jest sytuacja, w której oba atomy są tego samego rodzaju - wówczas elektrony wiążące znajdują się dokładnie pośrodku odległości między jądrami i wiązanie jest niespolaryzowane (nazywa się je też wiązaniem atomowym). Wiązanie atomowe występuje w cząsteczkach i kryształach pierwiastków niemetalicznych, na przykład F2, P4, diament, krzem, siarka.
Różnica elektroujemności i/lub promieni atomowych, występująca w przypadku, gdy wiązanie łączy dwa różne atomy, powoduje, że para wiążąca nie znajduje się już dokładnie pośrodku odległości między jądrami. Wiązanie staje się spolaryzowane: atom, który jest bliżej tej pary, przyjmuje polaryzację ujemną, a ten, który jest dalej - dodatnią.
Wiązania kowalencyjne (atomowe) powstają z elektronów obu atomów. Każdy atom może wnieść do wiązania wkład w postaci na przykład jednego elektronu - wówczas powstanie jedno wiązanie σ i atomy połączą się wiązaniem pojedynczym. Taka sytuacja ma miejsce na przykład w cząsteczce wodoru lub w krysztale diamentu. Jeśli atomy dysponują wystarczającą liczbą elektronów i orbitali walencyjnych, może dojść do uwspólnienia dalszych elektronów. Na przykład w cząsteczce azotu każdy z atomów wnosi do wiązania trzy elektrony: z pierwszej pary powstaje wiązanie σ, z drugiej - wiązanie π, a z trzeciej - drugie wiązanie π. Dzięki temu atomy azotu są połączone w cząsteczce N2 wiązaniem potrójnym.
Wiązanie kowalencyjne spolaryzowane może poza tym powstawać w mechanizmie donorowo-akceptorowym, kiedy atom ubogi w elektrony, ale dysponujący wolnym orbitalem, może przyjąć parę elektronową od atomu bogatego w elektrony. Zgodnie z takim mechanizmem powstają wiązania między atomem/jonem centralnym a ligandami w związkach kompleksowych, a także między atomem fluoru a atomami boru w BF3 oraz między atomem tlenu a atomem węgla w CO:
Mimo odmiennego mechanizmu powstawania, wiązanie donorowo-akceptorowe ma charakter wiązania kowalencyjnego spolaryzowanego. Widać to na przykład w jonie amonowym, który powstaje dzięki przyłączeniu jonu H+ (dysponującego wolnym orbitalem 1s) do cząsteczki amoniaku (dysponującej wolną parą elektronową, zlokalizowaną na atomie azotu). W powstałym jonie NH4+ w żaden sposób nie można rozpoznać, który z atomów wodoru przyłączył się jako proton do cząsteczki NH3. Z pomiarów strukturalnych wynika, że jon amonowy jest idealnie symetrycznym tetraedrem (hybrydyzacja azotu sp3) - wszystkie odległości między atomami wodoru a azotem są jednakowe, co świadczy o istnieniu w jonie czterech jednakowych wiązań N-H.
Wiązanie jonowe
Jak wspomniano wcześniej (trójkąt wiązań), wiązanie jonowe powstaje między atomami pierwiastków o znacznej różnicy elektroujemności, np. w związkach litowców i berylowców z lżejszymi fluorowcami. Różnica ta powoduje, że wskutek silniejszego przyciągania elektronów przez atom bardziej elektroujemny, maksimum gęstości elektronowej przesuwa się mocno w kierunku tego atomu - prawdopodobieństwo znalezienia się elektronu w pobliżu tego atomu jest znacznie większe, niż w pobliżu atomu o mniejszej elektroujemności.
Powstawanie wiązania jonowego opisuje np. model sferycznych jonów, oparty na następujących założeniach:
W atomie litowca występuje jeden elektron walencyjny, znajdujący się nad zamkniętą powłoką, która ma symetrię sferyczną i jest wysoce trwała. Dlatego pierwszy potencjał jonizacji takiego atomu jest niski - łatwo oderwać ten elektron i przeprowadzić atom w kation. Z kolei w atomie fluorowca znajduje się niezapełniona do końca powłoka, w której brakuje jednego elektronu. Atom fluorowca wykazuje więc tendencję do przyjęcia jednego elektronu i utworzenia anionu z wysoce symetryczną i trwałą, całkowicie zapełnioną powłoką. W związku z tym zbliżenie atomów litowca do atomów fluorowca może zaowocować przekazaniem łatwego do oderwania elektronu walencyjnego litowca do atomu fluorowca o wysokim powinowactwie elektronowym. Koszt energetyczny tego procesu (energia jonizacji litowca) jest pokrywany dzięki powinowactwu elektronowemu fluorowca, a dodatkową stabilność zapewnia powstałemu układowi przyciąganie elektrostatyczne między powstałymi różnoimiennymi jonami.
Siłom elektrostatycznego przyciągania, odpowiedzialnym za zbliżanie się obu jonów, przeciwstawiają się kwantowomechaniczne siły odpychania między zapełnionymi powłokami elektronowymi jonów. Dzięki temu ustala się stan równowagi, odpowiadający takiej odległości (równowagowej re) między jonami, przy której układ osiąga minimum energii. Otrzymujemy charakterystyczną krzywą potencjalną zależności energii układu od odległości między jonami.
Asymetria i asymptotyczność powyższej krzywej oznaczają, że po dostarczeniu odpowiedniej ilości energii do układu wzniesie się on ponad barierę energetyczną i jego komponenty będą mogły oddalić się do nieskończoności. Nastąpi dysocjacja związku; energia potrzeba do przekroczenia tej bariery nazywa się energią dysocjacji.
W środowisku polarnym, takim jak roztwór wodny, energia na dysocjację związku jest dostarczana przez proces solwatacji. Indywiduum polarne, czyli kation, anion lub dipol będzie podlegać oddziaływaniom polarnych cząsteczek rozpuszczalnika, czyli będzie solwatowany. Proces ten oznacza często powstanie akwakompleksów, czyli nowych wiązań, i dlatego jest zawsze egzoergiczny. Najczęściej pokrywa to z nawiązką koszt energetyczny dysocjacji związku.
Jeśli - zgodnie z modelem sferycznych jonów - potraktujemy jony jako „naładowane kulki”, wówczas otrzymamy równomierny rozkład linii sił pola elektrycznego tworzonego przez te jony - we wszystkich kierunkach przestrzeni.
Oznacza to, że każdy jon może przyciągać jony przeciwnego znaku z dowolnego kierunku, czyli wiązanie jonowe jest bezkierunkowe. Zaprezentowane na rysunku oddziaływanie pary różnoimiennych jonów wykazuje, że w przypadku takiej pary nie może nastąpić pełna wzajemna kompensacja linii sił pola elektrycznego („urwane” strzałki). Wiązanie jonowe charakteryzuje się zatem brakiem wysycenia, który pociąga za sobą rozszerzenie oddziaływania poszczególnych jonów na wszystkie kierunki przestrzeni, czyli jego delokalizację.
Powyższe cechy wiązania jonowego powodują, iż energetycznie korzystne jest, by każdy jon otoczony był w krysztale maksymalną możliwą liczbą jonów przeciwnego znaku. Liczba ta jest ograniczona po pierwsze miejscem dostępnym wokół jonu (czyli jego promieniem), a po drugie siłami elektrostatycznego odpychania między równoimiennymi jonami. Trwałość układu jest uzyskiwana przy określonej wzajemnej koordynacji jonów, przy czym w odróżnieniu od związków kowalencyjnych liczba koordynacji w związkach jonowych nie zależy od konfiguracji elektronowych poszczególnych pierwiastków, a jedynie od rozmiarów jonów. Budowa przykładowych związków jonowych jest przedstawiona w poniższej tabeli.
Stosunek promienia kationu do promienia anionu |
Typ koordynacji (przedział stosunku promieni) |
Przykład |
LK kationu |
LK anionu |
0,54 |
oktaedryczna (0,41÷0,73) |
NaCl |
6 |
6 |
0,91 |
kubiczna (0,73÷1,37) |
CsCl |
8 |
8 |
Parametrem opisującym trwałość sieci jonowej jest energia sieci krystalicznej. W jonowej sieci krystalicznej występują następujące oddziaływania:
kulombowskie przyciąganie różnoimiennych jonów,
przyciąganie van der Waalsa,
kulombowskie odpychanie równoimiennych jonów,
kwantowomechaniczne odpychanie zapełnionych powłok elektronowych.
W trwałej sieci efekty przyciągania przeważają nad efektami odpychania, a odległości między jonami stanowią wypadkową przyciągania i odpychania. Struktura równowagowa jest maksymalnie trwała, odpowiada jej minimum energii.
Miarą trwałości sieci jest zmiana energii w procesie rozpadu jednego mola kryształu w temperaturze 0 K. Proces rozpadu polega na oddaleniu się do nieskończoności jonów w stanie podstawowym. Wielkość ta nazywa się energią jonowej sieci krystalicznej.
Wiązanie metaliczne
Substancje zawierające wiązanie metaliczne charakteryzują się wyraźnie odmiennymi właściwościami w porównaniu z substancjami jonowymi i kowalencyjnymi. Właściwości te - wysokie przewodnictwo cieplne i elektryczne - wynikają z obecności w krysztale swobodnych nośników energii - swobodnych elektronów. Elektrony te są elektronami walencyjnymi atomów metalu, które - przynajmniej część z nich - łatwo jest oderwać. Kryształ metalu stanowi zatem zbiór kationów metalu, powiązanych przez poruszające się między nimi swobodnie elektrony, zwane „gazem”, „chmurą” lub „morzem” elektronowym.
Elektrony te wiążą kationy metalu niezależnie od kierunku w przestrzeni, wiązanie metaliczne jest zatem bezkierunkowe. Skoro elektrony mogą przemieszczać się swobodnie po całej sieci krystalicznej (co odpowiada za przewodnictwo cieplne i elektryczne metali), wiązanie metaliczne musi się na całą tę sieć rozciągać, czyli jest zdelokalizowane. A czy jest wysycone? Rozpatrzmy je z punktu widzenia teorii orbitali molekularnych. W metodzie LCAO MO, czyli tworzenia orbitali molekularnych metodą liniowej kombinacji orbitali atomowych, powstaje tyle samo MO, ile AO wzięto do kombinacji (taka jest natura matematyczna liniowej kombinacji funkcji). Jeśli uwzględnimy fakt, że np. atom litu ma 4 orbitale atomowe, to w krysztale zawierającym n atomów powstanie 4n orbitali molekularnych, które mogą pomieścić 8n elektronów. Z drugiej strony atom litu ma 1 elektron walencyjny, więc n atomów wnosi do tego układu n elektronów i jest oczywiste, że wiązanie metaliczne jest niewysycone.
Skąd biorą się owe nietypowe właściwości metali? Odpowiedź daje np. pasmowa teoria budowy kryształu. Zgodnie z powyższym rozważaniem, liczba stanów energetycznych w krysztale, czyli liczba MO, jest proporcjonalna do liczby atomów w tym krysztale:
Wysoka gęstość metalu powoduje, że poszczególne atomy w krysztale znajdują się bardzo blisko siebie, więc i różnice między poziomami energetycznymi poszczególnych MO są znikomo małe - zamiast zbioru orbitali molekularnych powstaje pasmo, a tworzące je MO są zdelokalizowane na cały kryształ (gdyż pasmo powstało z AO wszystkich atomów w krysztale).
Pasma w krysztale metalu powstają z AO analogicznego typu (analogicznej symetrii), mogą więc istnieć pasma s, p d i f (odpowiednio o pojemności 2n, 6n, 10n i 14n elektronów). Pasmo, które obsadzają elektrony wiążące (walencyjne), nazywa się pasmem walencyjnym. Pasmo wyższe - nieobsadzone - to pasmo przewodnictwa. Różnica energetyczna między tymi dwoma pasmami zależy od struktury elektronowej atomów i symetrii sieci krystalicznej i stanowi tzw. pasmo zabronione. Wielkość tej różnicy decyduje o tym, czy elektrony tworzące wiązanie mogą się łatwo przedostać z pasma walencyjnego na pasmo przewodnictwa i uzyskać swobodę ruchu, czy też nie. W związku z tym szerokość pasma zabronionego, oznaczana jako ΔE, decyduje o tym, czy dana substancja jest izolatorem (dielektrykiem, ΔE>3 eV), półprzewodnikiem (0,1 eV<ΔE<3 eV) czy przewodnikiem. W kryształach metalicznych pasmo przewodnictwa nakłada się na pasmo walencyjne i elektrony nie napotykają żadnej bariery energetycznej.
Stan podstawowy kryształu, czyli obsadzenie najniższych poziomów energetycznych, uzyskiwany jest w temperaturze 0 K. Najwyższy obsadzony poziom w temperaturze 0 K nazywa się poziomem Fermiego. W przypadku metalu poziom Fermiego mieści się w zakresie pasma przewodnictwa. Wzrost temperatury powoduje wzrost energii kryształu i przejście elektronów na coraz wyższe poziomy energetyczne. Wskutek tego procesu liczba częściowo choćby zapełnionych poziomów energetycznych wzrośnie i zmniejszy się swoboda ruchu nośników ładunku. Dlatego przewodnictwo metali maleje ze wzrostem temperatury (opór rośnie).
W przypadku półprzewodników sytuacja jest odwrotna, ponieważ wzrost temperatury i energii kryształu, pociągające za sobą przejścia elektronów na wyższe poziomy energetyczne, oznaczają, że coraz więcej elektronów pokonuje pasmo zabronione, przechodząc z pasma walencyjnego na pasmo przewodnictwa. Stężenie swobodnych nośników ładunku w paśmie przewodnictwa rośnie, więc i samo przewodnictwo półprzewodnika będzie wzrastać ze wzrostem temperatury. Oczywiście stężenie to można zmieniać także innymi metodami, np. przez domieszkowanie półprzewodnika pierwiastkami zawierającymi inną liczbę elektronów walencyjnych.
Inne typy wiązań
Jak wspomniano wcześniej, obok opisanych trzech zasadniczych typów wiązań wyróżnia się pewne podtypy o większym znaczeniu. Np. podtypem wiązania kowalencyjnego spolaryzowanego jest wiązanie donorowo-akceptorowe. Wiązanie tego typu może powstać zawsze, gdy możliwy jest kontakt między atomem lub cząsteczką mającą wolne orbitale, a atomem lub cząsteczką mającą dostępne pary elektronowe (zazwyczaj wolne pary elektronów niewiążących). Atom/cząsteczka przyjmująca elektrony na pusty orbital jest akceptorem, zaś atom/cząsteczka dostarczająca tych elektronów - donorem.
Wiązania tego typu mogą powstawać w następujących przypadkach:
Akceptor |
Donor |
Przykład związku |
Kation (H+, metal) |
Cząsteczka polarna posiadająca wolne pary elektronowe (NH3, H2O) |
NH4+, [Ni(OH2)6]2+ |
Kation (metalu) |
Anion (CN-, Cl-) |
[Fe(CN)6]3- |
Atom (metalu) |
Cząsteczka polarna posiadająca wolne pary elektronowe (CO) |
[Cr(CO)6] |
Atom (metalu) |
Anion (CN-) |
[Ni(CN)4]4- |
Cząsteczka (BF3) |
Cząsteczka polarna (NH3) |
H3N→BF3 |
Cząsteczka (BF3) |
Anion (F-) |
[BF4]- |
Uogólniając, można powiedzieć, że wiązanie donorowo-akceptorowe powstaje wskutek różnych oddziaływań: jon-dipol, atom-dipol, atom-jon, jon-jon i dipol-dipol. Zasadniczą przyczyną tych oddziaływań jest jednak zawsze elektrostatyczne przyciąganie różnoimiennych ładunków/biegunów dipoli.
Powstawanie wiązania donorowo-akceptorowego ma zasadnicze znaczenie dla chemii związków kompleksowych, czyli chemii koordynacyjnej. Wbrew jednak utartym przekonaniom chemia koordynacyjna nie dotyczy wyłącznie pierwiastków bloku d i f. W istocie większość związków nieorganicznych można rozpatrywać jako związki koordynacyjne, co jest możliwe przede wszystkim dlatego, iż wiązanie donorowo-akceptorowe ma charakter kowalencyjnego spolaryzowanego.
Związki kompleksowe tworzą nie tylko metale, ale również niemetale, np. cząsteczka jodu tworzy kompleksy z takimi donorami elektronów, jak amoniak, benzen czy eter dimetylowy.
Oddziaływania donorowo-akceptorowe często powodują przejście substancji ze stanu gazowego w ciekły i stały, ponieważ umożliwiają powstanie struktur o większej złożoności i masie cząsteczkowej. Np. difluorek berylu w stanie gazowym występuje w postaci pojedynczych liniowych cząsteczek BeF2, jednak dzięki obecności wolnych orbitali atomu berylu i par elektronowych fluoru może polimeryzować - wiązania między cząsteczkami powstają w mechanizmie donorowo-akceptorowym.
Istnieje pewna grupa związków o polarnej cząsteczce, które charakteryzują się nietypowymi właściwościami fizycznymi na tle swoich szeregów homologicznych. Najbardziej spektakularnym przykładem jest pod tym względem woda, która zachowuje stan ciekły w temperaturze pokojowej mimo ponaddwukrotnie mniejszej masy cząsteczkowej w porównaniu z siarkowodorem (gaz w warunkach normalnych). Przyczyną tego typu anomalii jest dodatkowe wiązanie, które łączy poszczególne cząsteczki substancji - wiązanie wodorowe.
Wiązanie tego typu powstaje w sytuacji, gdy w polarnej cząsteczce występuje z jednej strony atom wodoru jako dodatni biegun dipola - a zatem połączony wiązaniem silnie spolaryzowanym z atomem o wysokiej elektroujemności; zaś z drugiej strony - wysoce elektroujemne atomy dysponujące wolnymi parami elektronowymi, jako ujemne bieguny dipoli. W takiej sytuacji pojawia się oddziaływanie elektrostatyczne między dipolami, a atom wodoru staje się jakby szyną, po której elektrony donora przesuwają się w kierunku elektroujemnego atomu, z którym wodór jest połączony. Jest to możliwe tylko w przypadku atomów o niewielkich rozmiarach i posiadających mało „własnych” elektronów - atomów wodoru i litu. Tworzy się w ten sposób międzycząsteczkowe wiązanie wodorowe o sile dużo większej, niż wynikająca z samego oddziaływania elektrostatycznego między dipolami. Następuje łączenie się - asocjacja - cząsteczek.
Międzycząsteczkowe wiązanie wodorowe może tworzyć się zarówno między cząsteczkami tego samego związku - wody, amoniaku, fluorowodoru, jak i różnych związków, jak na przykład w roztworze wodnym amoniaku czy kwasu fluorowodorowego. Oddziaływanie to jest słabsze od zwykłego wiązania (na przykład kowalencyjnego), ale względnie silne. Kwasy karboksylowe nawet w stanie pary występują jako dimery, a fluorowodór - jako wyższe asocjaty.
Charakterystyczną cechą wiązania wodorowego jest jego asymetria. W przeciwieństwie do zwykłych wiązań donorowo-akceptorowych, które po utworzeniu są nieodróżnialne od wiązania kowalencyjnego spolaryzowanego, obie części wiązania wodorowego wyraźnie różnią się od siebie pod względem długości i siły, na przykład w cząsteczce wody:
O ile wiązanie wodorowe jest słabsze od zwykłych wiązań chemicznych, jest zarazem znacznie silniejsze niż oddziaływania van der Waalsa. Jego obecność ma też poważne konsekwencje dla właściwości fizykochemicznych związku, przejawiające się przede wszystkim nietypowym podwyższeniem temperatur topnienia i wrzenia substancji.
Oprócz międzycząsteczkowych wiązań wodorowych mogą powstawać również wiązania wewnątrzcząsteczkowe. Jest to możliwe przede wszystkich w przypadku bardziej złożonych związków organicznych, których cząsteczki mogą charakteryzować się budową umożliwiającą zbliżenie atomu donora i atomu wodoru-akceptora na odpowiednią odległość.
Bardzo spektakularnym przykładem wpływu obecności wiązania wodorowego i jego rodzaju na właściwości związku jest nitrofenol: odmiana orto, w której ze względów przestrzennych powstaje wewnątrzcząsteczkowe wiązanie wodorowe, blokujące częściowo możliwość tworzenia się asocjatów, ma temperaturę topnienia 45 ºC - o wiele niższą, niż odmiany meta (tt. 97 ºC) i para (tt. 114 ºC), w przypadku których wewnątrzcząsteczkowe wiązanie wodorowe nie powstaje, ale tworzy się za to między różnymi cząsteczkami:
Wiązanie wodorowe odgrywa bardzo istotną rolę w przypadku wielkocząsteczkowych związków organicznych, zwłaszcza białek i kwasów nukleinowych. Właśnie wiązania wodorowe decydują o drugo- i trzeciorzędowej strukturze białek. W cząsteczce DNA komplementarne nici nukleotydów również połączone są wiązaniami wodorowymi, które powstają między odpowiednimi zasadami azotowymi.
Podsumowanie wiązań |
||||
Cecha |
Wiązanie jonowe |
Wiązanie kowalencyjne i kowalencyjne spolaryzowane, także donorowo-akceptorowe |
Wiązanie metaliczne |
|
|
|
Wiązanie dwucentrowe |
Wiązanie wielocentrowe |
|
Kierunkowość |
Bezkierunkowe |
Kierunkowe |
Kierunkowe |
Bezkierunkowe |
Wysycenie |
Niewysycone |
Wysycone |
Niewysycone |
Niewysycone |
Lokalizacja |
Zdelokalizowane |
Zlokalizowane |
Zdelokalizowane |
Zdelokalizowane |
Inne rodzaje oddziaływań - siły van der Waalsa
Przejście substancji ze stanu gazowego w ciekły, czyli skroplenie, jest możliwe przede wszystkim dzięki temu, że między cząsteczkami występują pewne oddziaływania. Siły te nie mają charakteru zwykłych wiązań, co można rozpoznać dzięki ich większemu zasięgowi - większa jest też odległość równowagowa, co wskazuje na mniejszą siłę takich oddziaływań. Oddziaływania takie występują między cząsteczkami polarnymi (dipolami lub kwadrupolami), niepolarnymi cząsteczkami wysyconymi walencyjnie (na przykład CO2, I2), a nawet między atomami (w przypadku gazów szlachetnych). Z uwagi na ich powszechność, tego typu oddziaływania międzycząsteczkowe nazywa się oddziaływaniami uniwersalnymi; inna nazwa to oddziaływania (wiązania) van der Waalsa.
Krzywa energii potencjalnej „wiązania” van der Waalsa wyraża równowagę między przyciągającym oddziaływaniem chmur elektronowych atomów/cząsteczek, a siłami elektrostatycznego i kwantowomechanicznego odpychania tychże. Miarą siły oddziaływań międzycząsteczkowych może być entalpia parowania (cieczy) lub sublimacji (ciała stałego).
Międzycząsteczkowe oddziaływanie uniwersalne z wynika wzajemnego zaburzenia chmur elektronowych oddziałujących cząsteczek. W rezultacie energia układu obniża się proporcjonalnie do tego zaburzenia. Taki mechanizm wyjaśnia uniwersalny charakter sił van der Waalsa, ponieważ praktycznie wszystkie atomy i cząsteczki mają elektrony.
Jak wynika z obliczeń kwantowomechanicznych, w siły międzycząsteczkowe mają wkład oddziaływania elektrostatyczne (zaburzenia pierwszego rzędu) oraz indukcyjne i dyspersyjne (zaburzenia drugiego rzędu).
Oddziaływania elektrostatyczne obejmują indywidua chemiczne mające ładunek elektryczny (jony) lub moment elektryczny (dipolowy, kwadrupolowy lub inny). Oddziaływanie jonów lub cząsteczek prowadzi do takiej ich orientacji, przy której układ osiąga minimum energii. Jednak tego typu oddziaływania podlegają wpływowi temperatury, ponieważ ze wzrostem temperatury rośnie średnia energia kinetyczna cząsteczek, co utrudnia orientację.
Cząsteczka mająca trwały ładunek lub moment elektryczny indukuje w jonie lub innej cząsteczce (polarnej lub niepolarnej) dodatkowy moment elektryczny, co obniża energię potencjalną oddziałujących cząsteczek lub jonów i wzmacnia oddziaływanie międzycząsteczkowe, wnosząc do niego wkład indukcyjny. Oddziaływanie indukcyjne nie zależy od temperatury, ponieważ orientacja dipola indukowanego jest zależna wyłącznie od orientacji dipola indukującego; nie jest też addytywne.
Oddziaływanie tego typu odgrywa zasadniczą rolę podczas tworzenia klatratów gazów szlachetnych oraz w roztworach substancji polarnych w niepolarnych rozpuszczalnikach.
Indywidua chemiczne o symetrycznym rozkładzie ładunku, takie jak atomy gazów szlachetnych, nie oddziałują elektrostatycznie, nie mają bowiem ani ładunku, ani momentu elektrycznego. Wykazują jednak ściśliwość, umożliwiającą ich skroplenie i zestalenie. Odpowiedzialny jest za to ostatni rodzaj sił międzycząsteczkowych - oddziaływania dyspersyjne. Występują one także we wszystkich opisanych wcześniej przypadkach, jednak są wtedy maskowane przez silniejsze od nich oddziaływania indukcyjne lub silniejsze od obu typów oddziaływania elektrostatyczne.
Istnienie oddziaływań dyspersyjnych jest wytłumaczalne wyłącznie na gruncie mechaniki kwantowej. Elektrony w atomach i cząsteczkach traktuje się jako oscylujące wokół jąder atomowych. Oscylatory elektronowe o takiej samej częstotliwości oscylacji, zbliżone do siebie, wpadają w rezonans. W rezultacie sumaryczna energia zerowa oscylatorów ulega obniżeniu.
Właśnie oddziaływania dyspersyjne są przyczyną uniwersalności sił van der Waalsa, ponieważ wszystkie atomy i cząsteczki mają poruszające się elektrony. Oddziaływania dyspersyjne są ponadto addytywne, tzn. większa liczba oscylatorów oznacza większą siłę oddziaływań. Dlatego siła oddziaływań van der Waalsa rośnie ze wzrostem liczby elektronów w atomach i cząsteczkach, czyli największa jest dla makrocząsteczek.
Energia sił van der Waalsa jest dużo niższa od energii zwykłych wiązań, dlatego związki, w których siły te odgrywają główną rolę, są zwykle nietrwałe w temperaturze pokojowej (na przykład klatraty helowców). Istnieją jednak vanderwaalsowskie związki trwałe w podwyższonej temperaturze, na przykład kompleks trinitrobenzenu z naftalenem.
Typy wiązań w krysztale a właściwości substancji
Podobnie, jak wiązania chemiczne, kryształy klasyfikuje się według różnych kryteriów. Krystalografa najbardziej interesuje struktura kryształu, a więc jego symetria. Dla chemika jednak bardziej interesujące są same właściwości fizykochemiczne związku, a o tych decydują w większym stopniu wiązania występujące w krysztale.
Uwzględniając kryterium typu wiązania, możemy wyróżnić dwie zasadnicze grupy kryształów: „jednolite” (zawierające wiązania jednego typu) i „mieszane” (zawierające wiązania dwóch lub więcej typów).
Kryształy jednolite
Do grupy kryształów jednolitych należą kryształy jonowe, metaliczne i kowalencyjne.
Kryształy jonowe charakteryzują się na ogół dużą trwałością, ale i dużą reaktywnością, zwłaszcza w środowiskach polarnych. Na ogół dobrze rozpuszczają się w rozpuszczalnikach polarnych, takich jak woda. W stanie stałym nie przewodzą prądu, ale w roztworze - owszem, ponieważ po ich rozpuszczeniu w polarnym rozpuszczalniku następuje dysocjacja i nośniki ładunku - jony - uzyskują swobodę ruchu. Większość substancji o kryształach jonowych charakteryzuje się wysokimi temperaturami topnienia i wrzenia; są to bez wyjątku substancje stałe w warunkach normalnych.
Kryształy metaliczne, tworzone przez metale, stopy metali (zawierające czasem związki międzymetaliczne) oraz związki o charakterze metalicznym (na przykład niektóre wodorki bloku d), charakteryzują się również dużą trwałością (wysoka energia sieci krystalicznej), ale ich reaktywność jest bardzo zróżnicowana (wystarczy porównać metale szlachetne i litowce). Charakteryzują się też zróżnicowanymi temperaturami topnienia i wrzenia, ale w warunkach normalnych są w przeważającej większości substancjami stałymi. Przewodzą prąd elektryczny i ciepło w stanie stałym i ciekłym (rtęć!). Są trudno rozpuszczalne w większości rozpuszczalników, chociaż mogą z nimi reagować, dając rozpuszczalne związki (na przykład metale aktywne z wodą).
Kryształy kowalencyjne tworzą przede wszystkim niemetale, które w warunkach normalnych występują w stanie stałym, takie jak węgiel (diament), bor, krzem. Kryształy takie są słabymi przewodnikami ciepła i nie przewodzą prądu. Charakteryzują się wyjątkowo wysokimi temperaturami topnienia; są bierne chemicznie i trudno rozpuszczalne. Należą też do substancji o wysokiej twardości.
W tej grupie można też wymienić kryształy koordynacyjne. Tworzą je substancje o wysoce polarnym wiązaniu, zawierające zarówno atomy z wolnymi orbitalami, jak i atomy z wieloma wolnymi parami elektronowymi. Związki takie tworzą często polimery liniowe, warstwowe lub sieciowe dzięki temu, że atomy z wieloma wolnymi parami elektronowymi tworzą mostki łączące dwa lub więcej atomów z wolnymi orbitalami. Do grupy tej należą między innymi takie połączenia, jak fluorki metali o niezbyt niskiej elektroujemności (na przykład glinu). Wiązania „mostkowe” powstają w mechanizmie donorowo-akceptorowym, są jednak nieodróżnialne od pozostałych.
Kryształy mieszane
Grupa kryształów mieszanych obejmuje znaczną liczbę kombinacji; poniżej omówiono najważniejsze.
Kryształy molekularne zawierają w węzłach sieci krystalicznej obojętne elektrycznie, wysycone walencyjnie cząsteczki. W obrębie cząsteczek istnieją zwykle wiązania kowalencyjne (azot N2, jod I2, fosfor P4) lub kowalencyjne spolaryzowane (CO2), niekiedy powstałe także w mechanizmie donorowo-ackeptorowym ([Cr(CO)6]). Zdarza się - zwłaszcza w przypadku związków organicznych - że cząsteczki zawierają dość skomplikowane systemy wiązań, na przykład naftalen. Jednak między cząsteczkami nie ma zwykłych wiązań - działają tam siły van der Waalsa. Z tego powodu energia sieci w krysztale molekularnym jest niska - poszczególne cząsteczki łatwo od siebie oddzielić, co pociąga za sobą niskie temperatury topnienia i wrzenia. Substancje tworzące kryształy molekularne często sublimują w warunkach normalnych.
Kryształy koordynacyjno-kowalencyjne tworzą substancje o polarnych cząsteczkach, które mogą tworzyć wiązania wodorowe (asocjować): woda, amoniak, fluorowodór. Asocjacja cząsteczek powoduje podwyższenie temperatur topnienia i wrzenia w porównaniu ze spodziewanymi. W takich kryształach zachowana zostaje asymetria wiązania wodorowego.
Kryształy koordynacyjno-jonowe tworzy wiele związków kompleksowych. Jednostka kompleksowa może być cząsteczką obojętną (wtedy związek tworzy kryształ molekularny), ale częściej jest kationem lub anionem. W sieci krystalicznej ładunek jednostki koordynacyjnej może być kompensowany przez aniony proste, kationy metali lub również aniony lub kationy kompleksowe. W takiej sytuacji w jednostce kompleksowej istnieje wiązanie koordynacyjne (czyli kowalencyjne spolaryzowane powstające w mechanizmie donorowo-akceptorowym), zaś między jonami, niezależnie od ich charakteru, powstaje wiązanie jonowe. Tego typu kryształy tworzy większość związków kompleksowych, na przykład hydraty soli metali bloku d.
Do ostatniej grupy kryształów mieszanych, jaką warto wymienić, należy grafit. Grafit tworzy kryształ o wysokim stopniu złożoności, w którym istnieją właściwie trzy rodzaje oddziaływań. Kryształ grafitu składa się z warstw o strukturze plastra miodu, tzn. utworzonych z sześcioczłonowych pierścieni stykających się bokami. Atomy węgla mają w tej warstwie hybrydyzację sp2 - każdy z nich tworzy trzy wiązania kowalencyjne σ z innymi atomami C. Trzeci, niezhybrydyzowany orbital p ma symetrię π i wraz z pozostałymi tego typu orbitalami tworzy zdelokalizowane wiązanie π, rozciągające się na całą warstwę. Elektrony tworzące to wiązanie mają dzięki temu swobodę ruchu i są odpowiedzialne za przewodnictwo elektryczne grafitu. Między warstwami działają tylko siły van der Waalsa; warstwy są więc związane o wiele słabiej, niż atomy w poszczególnych warstwach. Z tego powodu łatwo oddzielać płaszczyzny od siebie i grafit wykazuje łupliwość.
Elementy teorii grup
Zaawansowana teoria grup, zastosowana w chemii, pozwala chemikowi wyciągać istotne wnioski i analizować bądź przewidywać budowę związków chemicznych na podstawie operacji matematycznych, wykonywanych na orbitalach atomowych zgodnie z elementami symetrii, jakie dana cząsteczka posiada. Poznanie zasad stosowania tego formalizmu wymagałoby znacznie obszerniejszego wykładu. Tutaj ograniczymy się jedynie do zdefiniowania pojęć operacji i elementów symetrii oraz zasad określania grupy punktowej (symetrii) cząsteczki, co umożliwi analizowanie podobieństw symetrii różnych związków i wpływu symetrii cząsteczki na właściwości fizykochemiczne związku.
Operacje i elementy symetrii
Operacją symetrii nazywa się takie przekształcenie przestrzenne obiektu (na przykład cząsteczki), które odtwarza jego ułożenie początkowe (na przykład wyjściowe położenie atomów). Innymi słowy, w wyniku operacji symetrii powinniśmy otrzymać stan nieodróżnialny od początkowego. Na przykład jeśli rozpatrzymy kwadrat i oś przechodzącą przez niego w punkcie przecięcia przekątnych, prostopadłą do jego powierzchni, to przy obrocie o 90 stopni w prawo każdy z wierzchołków zostanie zastąpiony przez inny wierzchołek, który wcześniej znajdował się na lewo od niego. Osoba, która widziała ten kwadrat tylko przed i po wykonanej operacji symetrii, ale nie widziała samego obrotu, nie będzie w stanie stwierdzić, czy kwadrat był obracany.
Elementem symetrii jest obiekt geometryczny, względem którego wykonuje się operację symetrii. W powyższym przykładzie oś obrotu jest elementem symetrii operacji obrotu. Najważniejsze elementy symetrii i odpowiadające im operacje są wymienione w poniższej tabeli. Z punktu widzenia geometrii elementy symetrii mogą być prostą, płaszczyzną lub punktem.
Element symetrii |
Symbol |
Operacja symetrii |
Komentarz |
Element tożsamościowy |
E |
Przekształcenie tożsamościowe |
Element i operacja dodane ze względów matematycznych, dla zapewnienia komplementarności całej teorii. |
Oś obrotu |
Cn |
Obrót |
Obrót oznacza, że dany punkt przesuwa się po wycinku okręgu o określony kąt. |
Płaszczyzna odbicia |
σ |
Odbicie |
Odbicie oznacza przeniesienie punktu na przeciwną stronę płaszczyzny, na taką samą odległość od płaszczyzny, w jakiej znajdował się wcześniej. |
Środek inwersji |
i |
Inwersja |
Inwersja jest operacją analogiczną do odbicia; oznacza przeniesienie punktu na przeciwną stronę środka inwersji, na taką samą odległość od środka, w jakiej znajdował się wcześniej. |
Indeks n w symbolu osi obrotu oznacza tzw. krotność osi, obliczaną ze wzoru ![]()
. Na przykład przy obrocie o 90º n=4. Krotność osi jest istotnym parametrem, ponieważ identyfikacja osi o największej krotności i ustalenie ich liczby ma zasadnicze znaczenie dla określenia symetrii cząsteczki. Jeśli w cząsteczce istnieje tylko jedna oś o najwyższej krotności, nazywa się ona osią główną cząsteczki. W przypadku związków chemicznych najczęściej spotykane są osi od C2 do C6, odpowiadające obrotom o 180º, 120º, 90º, 72º i 60º. Zazwyczaj oś główna o krotności n generuje w cząsteczce istnienie n osi C2, prostopadłych do niej.
Płaszczyzny odbicia klasyfikuje się pod względem ich położenia wobec osi głównej. Płaszczyzny zawierające tę oś nazywane są wertykalnymi (pionowymi) i oznaczane σv. Ich liczba w cząsteczce równa jest krotności osi głównej. Płaszczyzny prostopadłe do tej osi nazywają się horyzontalnymi (poziomymi) i oznaczane σh (ich liczba jest równa liczbie osi o najwyższej krotności - zwykle 1). Płaszczyzny, które oś główna przecina pod innymi kątami, nazywają się diagonalnymi i są oznaczane symbolem σd.
Środek inwersji znajduje się w geometrycznym środku cząsteczki (jeśli w ogóle istnieje). O ile cząsteczki mogą zawierać wiele osi obrotu i płaszczyzn odbicia, środek inwersji może być tylko jeden.
Znajdowanie elementów symetrii
Identyfikacja i określenie wszystkich elementów symetrii w cząsteczce ma zasadnicze znaczenie dla dalszej analizy jej symetrii i określenie, do jakiej rodziny symetrii należy.
Aby danego typu element symetrii istniał w cząsteczce, jej atomy muszą spełniać określone warunki co do liczby i ułożenia w przestrzeni. Na przykład w przypadku wzoru ogólnego cząsteczki AB4 możemy wyróżnić cząsteczki tetraedryczne (takie jak metan) lub kwadratowe (czyli płaskie). Jest oczywiste, że różnica ułożenia atomów w przestrzeni spowoduje, iż mimo ich jednakowej liczby oba typy cząsteczek będą mieć inne elementy symetrii, czyli charakteryzować się odmienną symetrią.
Element symetrii |
Wymaganie w odniesieniu do cząsteczki |
Tożsamościowy |
Brak |
Oś obrotu |
Liczba atomów danego typu musi pasować do krotności osi, to znaczy, że aby w cząsteczce istniała oś C4, muszą w niej się znajdować cztery jednakowe atomy leżące na jednej płaszczyźnie. Atomy, które nie spełniają tego warunku, muszą leżeć na osi. |
Płaszczyzna odbicia |
Poza płaszczyzną symetrii mogą leżeć wyłącznie atomy, które występują w cząsteczce w liczbie parzystej. Muszą znajdować się po przeciwległych stronach płaszczyzny, tzn. na prostej prostopadłej do tej płaszczyzny. „Nieparzyste” atomy muszą leżeć na płaszczyźnie. |
Środek inwersji |
Atomy muszą leżeć parami naprzeciwko środka inwersji (tzn. na prostych, które przechodzą przez środek), czyli powinny występować parzyście. „Nieparzysty” atom musi leżeć w środku inwersji (siłą rzeczy w cząsteczce może się więc znajdować tylko jeden taki atom). Jeśli cząsteczka ma więcej niż jeden atom „bez pary”, na pewno nie ma środka inwersji. |
Sprecyzujmy pojęcie „jednakowe atomy”. Czy wystarczy, aby były to atomy tego samego rodzaju, tzn. należące do jednego pierwiastka? Nie. Atomy muszą być równocenne, tzn. muszą ponadto zajmować takie samo położenie względem danego elementu symetrii. Prostokąt zawiera, tak samo jak kwadrat, cztery wierzchołki położone na jednej płaszczyźnie, ale nie ma w nim osi C4. Wierzchołki prostokąta nie są rozłożone równomiernie (symetrycznie), nie są równocenne, ale tworzą dwie równocenne pary. Dzięki temu prostokąt ma oś C2. W poszukiwaniu elementów symetrii istotne są zatem nie tylko grupy równocennych atomów, ale i równocenne grupy atomów.
Podsumowując:
znalezienie w cząsteczce n równocennych atomów, leżących na jednej płaszczyźnie, może oznaczać istnienie osi symetrii o krotności n, jeśli tylko wszystkie pozostałe atomy tej cząsteczki znajdą się na tej osi;
każda para równocennych atomów w cząsteczce może być związana z istnieniem płaszczyzny odbicia, położonej pośrodku odległości między nimi w taki sposób, że odcinek łączący te dwa atomy jest do niej prostopadły, jeśli tylko wszystkie pozostałe atomy cząsteczki leżą na tej płaszczyźnie lub odcinek łączący każdą parę równocennych atomów jest prostopadły do tej płaszczyzny i przecinany przez nią w połowie;
jeśli w cząsteczce nie ma nieparzystych atomów lub jest tylko jeden atom nieparzysty, może ona mieć środek inwersji, jeśli wszystkie pozostałe atomy można połączyć w pary równocennych, a odcinki łączące te pary przecinają się w jednym punkcie i w połowie; w punkcie tym może znajdować się nieparzysty atom.
Spróbujmy znaleźć wszystkie elementy symetrii dla kilku przykładowych cząsteczek.
Cząsteczka BF3 ma kształt trójkąta równobocznego. Główną osią jej symetrii jest prosta przechodząca przez punkt przecięcia środkowych, a krotność tej osi wynosi 3 (360º/120º). Oś główna o krotności 3 generuje trzy prostopadłe do niej osie C2, każda z nich przechodzi przez jeden z wierzchołków trójkąta i środek przeciwległego boku. Ponadto generuje też trzy płaszczyzny σv o analogicznym ułożeniu w przestrzeni. Poza tym BF3, jak każda cząsteczka płaska, ma płaszczyznę symetrii tożsamą z płaszczyzną cząsteczki, czyli prostopadłą do osi głównej, będzie to więc płaszczyzna σh. Innych elementów symetrii, poza tożsamościowym, cząsteczka BF3 nie posiada. Środka inwersji brak z uwagi na nieparzystą liczbę wierzchołków.
Cząsteczka benzenu C6H6 ma kształt sześciokąta foremnego. Główną osią jej symetrii jest prosta przechodząca przez punkt przecięcia przekątnych, a jej krotność wynosi 6, ponieważ dla odtworzenia położenia wierzchołków wystarczy obrót o 60º. Oś główna o krotności 6 generuje sześć prostopadłych do niej osi C2. Trzy z nich przechodzą przez parę przeciwległych wierzchołków sześciokąta, a pozostałe trzy - przez środki przeciwległych boków. Ponadto generuje też sześć płaszczyzn σv o analogicznym ułożeniu w przestrzeni. Poza tym benzen, jako cząsteczka płaska, ma płaszczyznę symetrii tożsamą z płaszczyzną cząsteczki, czyli prostopadłą do osi głównej, będzie to więc płaszczyzna σh. Wreszcie cząsteczka benzenu ma też środek inwersji, znajdujący się w punkcie przecięcia wszystkich osi symetrii.
W przypadku brył zadanie odnajdywania elementów symetrii zaczyna się komplikować, zwłaszcza w przypadku jednakowych wierzchołków. Wysoce symetryczne struktury trójwymiarowe mają bardzo dużo elementów symetrii i ich odnalezienie wymaga sporej wyobraźni przestrzennej. Przeanalizujmy hipotetyczną cząsteczkę o budowie prostopadłościanu o podstawie kwadratu (czyli wg terminologii stereochemicznej - pryzmatu kwadratowego; ostrosłup nazywa się w stereochemii piramidą).
Jest oczywiste, że osią główną pryzmatu kwadratowego będzie oś główna jego podstaw, czyli C4. Oś ta generuje cztery osie C2; dwie z nich przechodzą przez środki przeciwległych ścian pryzmatu, a dwie pozostałe - przez środki przeciwległych krawędzi bocznych. Ponadto oś główna C4 generuje istnienie czterech płaszczyzn symetrii σv; dwie z nich zawierają pary przeciwległych krawędzi bocznych (czyli przechodzą tak jak przekątne podstawy), a dwie pozostałe przechodzą przez środki przeciwległych boków podstawy. Pryzmat kwadratowy ma też płaszczyznę horyzontalną, która znajduje się w połowie jego wysokości i jest prostopadła do osi głównej, oraz środek inwersji, znajdujący się w punkcie przecięcia wszystkich osi. Być może to wniosek zaskakujący, ale pryzmat kwadratowy ma identyczny zestaw elementów symetrii, co kwadrat - a zatem również identyczną symetrię.
Jeszcze większe komplikacje pojawiają się w przypadku brył zawierających więcej osi o wysokiej krotności (wyższej niż 2). Na przykład sześcian zawiera następujące elementy symetrii:
trzy osie C4 (przechodzące przez środki boków);
cztery osie C3 (biegnące tak jak jego przekątne);
sześć osi C2 (przebiegających przez środki przeciwległych krawędzi);
trzy płaszczyzny ułożone prostopadle do osi C4, oznaczane jako σh;
sześć płaszczyzn, z których każda zawiera parę przeciwległych krawędzi, oznaczanych jako σd, ponieważ ani nie zawierają osi o najwyższej krotności, ani nie są do nich prostopadłe;
środek inwersji, znajdujący się w punkcie przecięcia przekątnych.
Grupy symetrii. Ustalanie symboli grup punktowych
istnieje płaszczyzna odbicia
istnieje środek inwersji (przypadek w związkach chemicznych niespotykany)
Opis orbitali z punktu widzenia symetrii
a i b oznaczają poziomy niezdegenerowane, czyli zawierające tylko jeden orbital;
e oznacza poziom dwukrotnie zdegenerowany;
t oznacza poziom trójkrotnie zdegenerowany
Symetria cząsteczki a właściwości związku
Uproszczenia a błędy w rozumieniu chemii
Wzory kreskowe, wartościowość i stopień utlenienia
koordynacyjną (sieci, łańcucha lub kryształu polimerycznego, w którym jony centralne są połączone mostkami tworzonymi przez ligandy);
jonową, w której kationy (aniony) kompleksowe są połączone z odpowiednimi anionami (kationami) siłami elektrostatycznymi.
Prawidłowe wzory strukturalne (kreskowe) anionów kwasów tlenowych
Wiązania chemiczne zawsze łączą co najmniej dwa atomy, a więc powstają między nimi i nie można ich rysować w postaci „luźnych” kresek, wolnych z jednej strony i prowadzących w próżnię. Wiązania nie mogą przypominać mostu w Avignon. Jeśli na drugim końcu zlokalizowanego wiązania nie ma żadnego atomu, wiązanie to nie istnieje!
Zgodnie z wynikami badań strukturalnych jon siarczanowy(VI) ma strukturę tetraedryczną. Tetraedr (czworościan) jest bryłą foremną, a zatem ma wszystkie ściany, krawędzie i kąty równe, a atom centralny musi znajdować się w jego geometrycznym środku, czyli być równoodległy od wszystkich atomów tlenu (wierzchołków tetraedru). Z drugiej strony wiadomo, że podwójne wiązanie siarka-tlen jest wyraźnie krótsze od pojedynczego wiązania S-O, wobec czego zasada równych odległości między siarką a wszystkimi czterema atomami tlenu nie byłaby w przytoczonym wzorze spełniona. Podobnie, jak w przypadku rozpatrywanego wcześniej wzoru kwasu azotowego(V), nie można się tu obejść bez koncepcji delokalizacji wiązań. Dzięki delokalizacji wiązań π otrzymujemy w siarczanie(VI) cztery jednakowe (równocenne) wiązania siarka-tlen, pośrednie między wiązaniem pojedynczym a podwójnym (i to dokładnie - rząd takiego wiązania wynosi 1,5).
Tetraedryczna symetria jonu SO42- obejmuje także rozkład ładunku. Zgodnie z badaniami strukturalnymi, nie można przypisać pełnego jednostkowego ładunku ujemnego żadnemu atomowi tlenu. Ładunek jest również zdelokalizowany na wszystkie atomy tlenu, podobnie jak ładunek dodatni jonu amonowego nie jest przypisany żadnemu konkretnemu atomowi wodoru, a jest rozproszony na wszystkie atomy wodoru w jonie NH4+. Delokalizacja wiązania jest w anionach kwasów tlenowych nierozerwalnie związana z delokalizacją ładunku, ponieważ atomy tlenu są w tych anionach dwuwartościowe. W cząsteczce kwasu siarkowego(VI) dwa atomy tlenu są połączone z atomem siarki wiązaniami podwójnymi, a dwa pozostałe tworzą po jednym wiązaniu z wodorem i siarką. W anionie siarczanowym(VI) każdy atom tlenu jest połączony z atomem siarki wiązaniem o rzędzie 1,5, a ponadto przypada nań „połówka” elektronu odpowiedzialnego za ładunek anionu (dwa elektrony są zdelokalizowane na cztery atomy tlenu), co łącznie daje „dwa” wiązania.
Sole „kwaśne” i „zasadowe”
w przypadku wodorosoli mocnego kwasu następuje (z wyjątkiem skrajnie stężonych roztworów) dysocjacja wodoroanionu, na przykład:
w przypadku wodorosoli słabego kwasu i mocnej zasady po dysocjacji następuje (z wyjątkiem roztworów skrajnie rozcieńczonych) hydroliza wodoroanionu:
w przypadku hydroksosoli mocnej zasady następuje dysocjacja hydroksokationu:
dysocjacja hydroksosoli słabej zasady i mocnego kwasu prowadzi do hydroksokationu, który ulega hydrolizie:
Karbid węglikiem?
Czy promocja jest wzbudzeniem?
Wzory nieoczywiste
Nazewnictwo związków nieorganicznych
z uwzględnieniem związków kompleksowychNazewnictwo i symbolika pierwiastków
Nazewnictwo związków chemicznych
Ogólne zasady nazewnictwa związków chemicznych
W przedrostkach oznaczających liczby atomów stosuje się wyłącznie liczebniki greckie: bi-, tri-, tetra- itd. lub bis-, tris-, tetrakis- itd. w przypadku złożonych ligandów w związkach kompleksowych.
Pierwiastki w związkach chemicznych mogą charakteryzować się dodatnim, ujemnym lub zerowym, całkowitym lub ułamkowym stopniem utlenienia. Stopień utlenienia podaje się cyframi rzymskimi (z wyjątkiem zera) z ewentualnym znakiem minus przed liczbą (znak plus pomija się): Al0, NaIO-IIClI, [Cr0(CIIO-II)6]. W obojętnej cząsteczce suma wszystkich stopni utlenienia pomnożonych przez liczby atomów jest równa zero; w jonie jest równa ładunkowi jonu.
W odróżnieniu od stopnia utlenienia ładunek jonu, który może przyjmować dodatnie lub ujemne wartości całkowite, podaje się w postaci liczby arabskiej z następującym po niej znakiem jonu (w prawym górnym indeksie). Jedynkę pomija się: H-, Cu2+, PO43-, O2+ itp.
Zgodnie z zalecanym przez Komisję Nomenklatury Polskiego Towarzystwa Chemicznego systemem Stocka stopień utlenienia podaje się w nazwie związku w nawiasie po nazwie pierwiastka (bez odstępu!). Stopień utlenienia pomija się, jeśli dany pierwiastek przyjmuje w związkach tylko jedną jego wartość (jak na przykład sód lub cynk).
Alternatywnym sposobem nazywania związków jest wskazanie liczb atomów tworzących cząsteczkę z użyciem odpowiednich liczebników greckich, na przykład: CO2 - ditlenek węgla, Fe2O3 - tritlenek diżelaza, SnI4 - tetrajodek cyny.
Rzadziej spotykanym systemem nazewnictwa jest system Ewansa-Basseta, wg którego po nazwie pierwiastka lub grupy pierwiastków (stanowiących osobny jon) podaje się w nawiasie okrągłym (bez odstępu!) ładunek jonu, na przykład FeCl2 - chlorek żelaza(2+). Podobnie, jak w systemie Stocka, robi się to tylko wtedy, gdy pierwiastek tworzy więcej jonów prostych: NaI - jodek ołowiu. W przeciwnym razie jedynki nie pomija się. W przypadku anionów kwasowych niezbędne jest podanie także liczby atomów tlenu: CuSO4 - tetraoksosiarczan(2-) miedzi(2+), Cu2SO3 - trioksosiarczan(2-) miedzi(1+).
We wzorach chemicznych na pierwszym miejscu umieszcza się zawsze pierwiastek mniej elektroujemny, a na drugim - bardziej elektroujemny. Nazwę związku tworzy się, podając składniki w odwrotnej kolejności.
W niektórych przypadkach, zwłaszcza w odniesieniu do związków spotykanych w życiu codziennym, dopuszczalne jest używanie nazw zwyczajowych, takich jak dwutlenek węgla, amoniak, woda, siarkowodór itp.
Nazewnictwo związków homopoliatomowych (wieloatomowych cząsteczek pierwiastków)
Nazewnictwo ważniejszych jonów
Kationy
Aniony
Nazewnictwo związków binarnych
Binarne związki wodoru
nazwy związków wodoru z pierwiastkami grup 14÷16 tworzy się, dodając do rdzenia nazwy (często łacińskiej) pierwiastka końcówkę „-an”, unikając jednocześnie podobieństwa do ewentualnych nazw anionów reszt kwasowych (na przykład tellan zamiast telluran):
nazwy związków wodoru z pierwiastkami grupy 17 tworzy się zgodnie z zasadami nazewnictwa innych związków binarnych:
nazwy związków boru z wodorem, stanowiących liczną grupę związków o zróżnicowanej strukturze, tworzy się na podstawie nazw typu „boran” lub borowodór, podając liczbę atomów boru w cząsteczce (z użyciem normalnych przedrostków) i -dla uzyskania jednoznaczności - liczbę atomów wodoru (wyjątkowo cyframi arabskimi w nawiasie okrągłym po nazwie związku, bez odstępu):
Binarne związki tlenu
zawierające atomy tego samego pierwiastka na różnych stopniach utlenienia; nazwę takiego związku tworzy się, wymieniając je w kolejności rosnącego stopnia utlenienia:
zawierające atomy różnych pierwiastków; nazwę takiego związku tworzy się, wymieniając te pierwiastki w kolejności alfabetycznej:
na -I stopniu utlenienia: nadtlenki
na ułamkowych ujemnych stopniach utlenienia (-½ - ponadtlenki i -1/3 - ozonki):
na dodatnich stopniach utlenienia:
Nazewnictwo związków wielopierwiastkowych
Kwasy
Kwasy beztlenowe
Oksokwasy
Kwasy traktowane jako związki kompleksowe
nazwa ligandu (nazwy ligandów) dołączonych do atomu centralnego z odpowiednimi przedrostkami liczbowymi,
rdzeń nazwy pierwiastka będącego atomem centralnym,
końcówka -owy,
stopień utlenienia pierwiastka będącego atomem centralnym (w razie potrzeby).
Nazwy wszystkich ligandów (czyli niekwasowych atomów wodoru i innych ligandów) dołączonych do atomu centralnego w kolejności alfabetycznej; w razie potrzeby poprzedzone odpowiednimi liczebnikami.
Nazwy wszystkich ligandów (czyli niekwasowych atomów wodoru i innych ligandów) dołączonych do atomu centralnego w kolejności alfabetycznej; w razie potrzeby poprzedzone odpowiednimi liczebnikami.
Rdzeń nazwy pierwiastka będącego atomem centralnym (niekiedy w języku polskim zmodyfikowany)
Rdzeń nazwy pierwiastka będącego atomem centralnym (niekiedy w języku polskim zmodyfikowany)
Końcówka -an lub -ian.
Końcówka -an lub -ian.
Liczba wyrażająca ładunek anionu (system Ewansa-Basseta) lub stopień utlenienia pierwiastka będącego atomem centralnym (system Stocka).
Wodorotlenki
Sole
Sole proste
Sole uwodnione
do nazwy soli, utworzonej zgodnie z pozostałymi zasadami, dodaje się po długiej kresce słowo „woda”, po którym w nawiasie podaje się liczbę cząsteczek wody przypadających na liczbę „cząsteczek” soli, na przykład:
przed nazwą soli (podawaną w dopełniaczu) umieszcza się słowo „hydrat” z odpowiednim przedrostkiem, określającym liczbę cząsteczek wody, przypadających na „cząsteczkę” soli:
Wodorosole
Sole podwójne, potrójne itd.
Oksosole
Hydroksosole
Sole będące tlenkami i wodorotlenkami podwójnymi, potrójnymi itd.
Podstawowe pojęcia chemii koordynacyjnej
Klasyfikacja i nomenklatura ligandów
Podział ligandów
Podział ze względu na naturę chemiczną - na ligandy organiczne (takie jak aminy, aniony kwasów karboksylowych, etery, EDTA, acetyloaceton) i ligandy nieorganiczne (jony halogenkowe, H-, O2-, O22-, O2-, woda, amoniak, CO, BH4-, aniony kwasów tlenowych itd.).
Podział ze względu na budowę - na ligandy proste (składające się z jednego atomu, na przykład H-, O2-, S2-, F-, Cl-, Br-, I-) i ligandy złożone (o cząsteczkach złożonych z wielu atomów, na przykład H2O, NH3, SO42-, CH3CO2-, bipirydyl itd.).
Podział ze względu na ładunek elektryczny - na ligandy anionowe (na przykład H-, O2-, O22-, O2-, BH4-, halogenki, aniony kwasowe) i ligandy obojętne (na przykład woda, amoniak, aminy, CO, fosfiny, arsyny, etery, ketony, alkohole).
Podział ze względu na liczbę atomów donorowych liganda. Pojęcie to nazywa się w polskojęzycznej literaturze dentnością, chelatowością lub kleszczowością; w niniejszym skrypcie stosowany jest pierwszy z tych terminów.
Ligandy monodentne, czyli zawierające jeden atom donorowy. Do tej grupy należą wszystkie ligandy proste, a ponadto: OH-, H2O, NH3 i monoaminy, PH3 i monofosfiny, proste etery, CO itd.
Ligandy polidentne, zawierające więcej niż jeden atom donorowy. W zależności od liczby tych atomów wyróżniamy ligandy bidentne (na przykład difos), tridentne (na przykład dietylenotriamina), tetradentne, heksadentne (na przykład EDTA) itd. Ligand o żądanej dentności można teoretycznie skonstruować w postaci odpowiedniej poliaminy etylenowej, polieteru etylowego (na przykład tridentny CH3CH2OCH2CH2OCH2CH2OCH2CH3) lub eteru koronowego.
Ligandy ambidentne. Jest to szczególna grupa ligandów polidentnych (najczęściej bidentnych), które mają wiele atomów donorowych, ale sztywna struktura cząsteczki uniemożliwia im koordynowanie danego atomu/jonu centralnego przez wszystkie atomy donorowe jednocześnie. Mogą one stanowić mostki w kompleksach wielordzeniowych; ponadto mogą koordynować dany atom/jon centralny na różne sposoby, na przykład w CN- rolę atomu donorowego może pełnić zarówno węgiel, jak i azot, w SCN- - azot lub siarka, w OCN- i NCO- - azot lub tlen.
Podział ze względu na symetrię elektronów donorowych liganda. Każdy ligand jest zawsze przede wszystkim donorem pary elektronowej. Pierwsze wiązanie koordynacyjne powstaje zawsze w kierunku L→M. Zależnie od natury pary elektronowej liganda, tworzącej to wiązanie, wyróżnia się:
Ligandy σ-donorowe, tj. te, które tworzą wiązanie z atomem/jonem centralnym za pomocą elektronów niewiążących (znajdujących się na orbitalach o symetrii σ). Należy do nich większość ligandów, na przykład OH-, Cl-, NH3, H2O, aniony kwasowe itd.).
Ligandy π-donorowe, tworzące wiązanie z atomem/jonem centralnym za pomocą elektronów wiążących z orbitali o symetrii π, na przykład: eten, benzen, anion cyklopentadienylowy.
Podział ze względu na naturę wiązania powstającego między ligandem a atomem/jonem centralnym. Jak wspomniano wcześniej, każdy ligand tworzy z atomem/jonem centralnym przede wszystkim wiązanie σ. Ponadto, jeśli istnieją sprzyjające warunki, między ligandem a pierwiastkiem centralnym może powstać wiązanie π (w mechanizmie donorowo-akceptorowym). Istnieją tu dwie możliwości. Gdy ligand obfituje w elektrony (tak jak na przykład jon chlorkowy, tlenkowy, siarczanowy(VI)), a atom/jon centralny dysponuje wolnymi orbitalami o odpowiedniej symetrii, w kompleksie powstaje wiązanie π L→M. Możliwa jest też odwrotna sytuacja - gdy atom/jon centralny jest bogaty w elektrony (dotyczy to przede wszystkim pierwiastków na niskich stopniach utlenienia), a w cząsteczce liganda występują puste orbitale molekularne o odpowiedniej symetrii, w kompleksie powstaje wiązanie π M→L. Najpewniejszą metodą ustalenia, czy dany ligand może tworzyć wiązanie π z atomem/jonem centralnym, jest narysowanie diagramu MO cząsteczki liganda i zbadanie, czy istnieją w nim orbitale HOMO lub LUMO o odpowiedniej symetrii i energii. W oparciu o to, jakie wiązania tworzy dany ligand z atomem/jonem centralnym, rozróżnia się trzy klasy ligandów:
(Czyste) σ-donory, które nie tworzą wiązań π. Przykłady: woda, amoniak, aminy, H-, siarkowodór.
π-donory, posiadające wysokoenergetyczne HOMO o symetrii π. Ligandy te tworzą wiązanie π L→M, czyli wykorzystują do tego „własne” elektrony. Do tej grupy należą wszystkie aniony kwasowe, aniony halogenkowe, O2-, O22-, O2- itd.
π-akceptory, posiadające niskoenergetyczne LUMO o symetrii π. Tworzą one wiązanie π M→L, czyli wykorzystują do tego elektrony pierwiastka centralnego. Przykładami takich ligandów są: N2, CO, CN-, fosfiny, arsyny.
Podział ze względu na siłę pola ligandów. Pole ligandów jest pojęciem z zakresu zaawansowanych teorii budowy związków koordynacyjnych - teorii pola krystalicznego i teorii pola ligandów. Mówiąc w uproszczeniu, gdy symetria otoczenia atomu/jonu centralnego odbiega od sferycznej (czyli w praktycznie każdym związku kompleksowym), stopień degeneracji poziomów orbitalowych tego atomu ulega zmniejszeniu. Jest to spowodowane oddziaływaniem elektronów, które mogą obsadzać orbitale, z ligandami (mającymi charakter anionów lub dipoli zwróconych biegunem ujemnym w kierunku atomu/jonu centralnego). Jeśli dany orbital znajduje się w przestrzeni bliżej ligandów, umieszczenie na nim elektronu (ujemnego) będzie wymagać wyższej energii. Gdy natomiast orbital atomowy jest oddalony od ligandów, umieszczenie na nim elektronu jest łatwiejsze, to jest wymaga niższej energii. Dzięki temu orbitale atomowe atomu/jonu centralnego ulegają rozszczepieniu. Na przykład gdy w cząsteczce kwadratowej ligandy leżą na osiach X i Y układu kartezjańskiego, orbitale px i py znajdują się bliżej ligandów, zaś orbital pz - dalej. Wskutek tego poziom orbitalowy p rozszczepia się na dwa podpoziomy: niżej energetyczny, obejmujący tylko orbital pz, i dwukrotnie zdegenerowany wyżej energetyczny, składający się z orbitali px i py. Różnica energii między tymi podpoziomami nazywa się parametrem rozszczepienia (oznaczanym na przykład Δo w kompleksach oktaedrycznych i Δt w kompleksach tetraedrycznych) i stanowi miarę siły pola ligandów.
Ligandy słabego pola, powodujące względnie niewielkie rozszczepienie orbitali atomu/jonu centralnego. Należą do nich praktycznie wszystkie π-donory.
Ligandy silnego pola, powodujące duże rozszczepienie orbitali atomu/jonu centralnego. Należą do nich wszystkie π-akceptory.
Ligandy średniego pola, do których zalicza się większość czystych σ-donorów.
Nazewnictwo ligandów
Klasyfikacja związków kompleksowych
Kompleksy kationowe, takie jak [Cr(H2O)6]3+, [Ni(NH3)6]2+. Mogą je tworzyć pierwiastki na dodatnich stopniach utlenienia z ligandami obojętnymi.
Kompleksy anionowe. Mogą je tworzyć pierwiastki na zerowym ([Ni(CN)4]4-) lub dodatnich stopniach utlenienia z ligandami anionowymi ([BH4]-, [Fe(CN)6]3-, [SO4]2-, [PF6]-, [MnO4]-) lub pierwiastki na ujemnych stopniach utlenienia z ligandami obojętnymi ([Co(CO)4]-).
Kompleksy obojętne. Mogą je tworzyć pierwiastki na zerowym stopniu utlenienia z ligandami obojętnymi (na przykład [Fe(CO)5], [Mo(N2)2(dppe)2]) lub pierwiastki na dodatnich stopniach utlenienia z ligandami anionowymi (na przykład [WH4(dppe)2]).
Kompleksy jednordzeniowe, zawierające jeden atom/jon centralny, na przykład [Cr(NH3)6]3+, [PtCl6]2-.
Kompleksy wielordzeniowe, zawierające co najmniej dwa atomy/jony „centralne”, na przykład: dwurdzeniowe [Cu2(CH3CO2)4(H2O)2], [(NH3)5Cr(OH)Cr(NH3)5]5+; trzyrdzeniowe [Nb3Br8]; sześciordzeniowe [Ta6Cl12]2+.
Kompleksy niskospinowe - związki o maksymalnej liczbie sparowanych elektronów walencyjnych atomu/jonu centralnego (są to m.in. kompleksy z ligandami silnego pola - patrz następny podrozdział).
Kompleksy wysokospinowe - związki, w których elektrony walencyjne atomu/jonu centralnego obsadzają OM pochodzące od orbitali d atomu/jonu centralnego zgodnie z regułą Hunda (są to przeważnie kompleksy z ligandami słabego pola - patrz następny podrozdział).
Kompleksy paramagnetyczne, czyli o momencie magnetycznym różnym od zera. Są to związki, w których atom/jon centralny ma co najmniej jeden niesparowany elektron. Do tej grupy należą wszystkie związki pierwiastków, mających w kompleksie nieparzyste liczby elektronów walencyjnych: d1, d7 itd. oraz niektóre związki pierwiastków o parzystych konfiguracjach elektronowych, przede wszystkim kompleksy o wysokim stopniu degeneracji OM pochodzących od orbitali d atomu/jonu centralnego.
Kompleksy diamagnetyczne, czyli związki o momencie magnetycznym równym zero. Są to związki, w których atom/jon centralny ma wszystkie elektrony sparowane. Do tej grupy należą wszystkie związki pierwiastków na maksymalnym stopniu utlenienia, czyli na przykład z konfiguracją d0 oraz niektóre związki pierwiastków o parzystych konfiguracjach elektronowych, (o niskim stopniu degeneracji OM pochodzących od orbitali d atomu/jonu centralnego). Większość klasterów jest diamagnetykami, stąd diamagnetyzm stanowi czasem kryterium umożliwiające wykrywanie wiązania klasterowego.
Kompleksy wewnątrzorbitalowe - na przykład związki pierwiastków IV okresu, tworzących wiązania z ligandami z wykorzystaniem orbitali 3d; [Cr(CO)6].
Kompleksy zewnątrzorbitalowe - związki pierwiastków tworzących wiązania z ligandami z wykorzystaniem orbitali d o tej samej głównej liczbie kwantowej, co używane orbitale s i p. Do tej grupy należą kompleksy pierwiastków bloku p oraz pierwiastków dalszych grup bloku d, na przykład 10, 11, 12 (pierwiastków bogatych w elektrony, na przykład o konfiguracji d8 wysokospinowej, d9, d10.
Kompleksy labilne - związki, w których występują wolne orbitale d na poziomie orbitalowym wykorzystanym do tworzenia wiązań między atomem/jonem centralnym a ligandami. Sytuacja taka ułatwia wymianę ligandów na inne.
Kompleksy bierne - związki, w których brak wolnych orbitali d na poziomie orbitalowym wykorzystanym do tworzenia wiązań między atomem/jonem centralnym a ligandami.
Nazewnictwo prostych związków kompleksowych jedno- i wielordzeniowych
Nazwy kationowych, anionowych i obojętnych jednostek koordynacyjnych
Nazewnictwo kompleksów z ligandami polidentnymi
Nazewnictwo kompleksów wielordzeniowych
kompleksy z ligandami mostkowymi (stanowiącymi „łącznik” między dwoma atomami/jonami „centralnymi”);
kompleksy klasterowe (zawierające wiązanie między atomami/jonami „centralnymi”);
kompleksy zawierające zarówno ligandy mostkowe, jak i wiązanie między atomami/jonami „centralnymi”.
Ligandy tworzące mostki wskazuje się w nazwie (i najlepiej również we wzorze) grecką literą μ z łącznikiem, na przykład μ-okso.
Całe wyrażenie określające mostek także oddziela się od reszty nazw łącznikami (w przypadku ligandów o bardziej skomplikowanych nazwach - nawiasami): amina-μ-okso-trisulfido.
Jeśli w cząsteczce występuje więcej niż jeden ligand mostkowy danego rodzaju, używa się odpowiednich przedrostków liczbowych: tri-μ-okso.
Liczbę centrów koordynacyjnych łączonych przez mostek oznacza się dolnym indeksem po μ (dwójkę najczęściej się pomija).
Ligandy mostkowe wymienia się w kolejności alfabetycznej wraz z innymi ligandami, jednak przed niemostkowymi ligandami tego samego typu, na przykład μ-okso-triokso.
Atomy/jony centralne wymienia się po ligandach w kolejności alfabetycznej, stosując w razie potrzeby odpowiednie przedrostki liczbowe.
Jeśli jednostka koordynacyjna jest anionem, nazwy atomów/jonów centralnych ujmuje się w nawias, po którym następuje końcówka an (ian) i liczba oznaczająca ładunek jonu.
Dla ułatwienia określania symetrii cząsteczki wykorzystuje się fakt, że cząsteczki o identycznych zestawach elementów symetrii mają identyczną symetrię (choć zdarza się, że mają odmienne kształty!). Charakterystyczne zestawy elementów symetrii nazywa się grupami symetrii lub grupami punktowymi. Dla pełnego określenia symetrii cząsteczki wystarczy zatem podanie symbolu grupy punktowej.
Grupy punktowe są oznaczane literami C, D, T, O, I lub S z odpowiednimi indeksami, informującymi o krotności osi głównej i/lub obecności środka inwersji lub płaszczyzn odbicia (i ich rodzaju). Poniżej przedstawiono algorytm określania grupy punktowej.
Stan symetrii w cząsteczce |
Grupa punktowa |
Brak elementów symetrii |
C1 |
Brak osi obrotów |
Cs Ci |
Istnieją osie, ale tylko niewłaściwe (przypadek w związkach chemicznych niespotykany) |
Sn |
Istnieje wiele osi o krotności wyższej od 2 (wysoce symetryczne cząsteczki o budowie jednej z pięciu brył platońskich) |
czworościan/tetraedr - Td ośmiościan/oktaedr - Oh sześcian - Oh dwunastościan/dodekaedr - Ih dwudziestościan/ikosaedr - Ih |
Istnieje oś Cn nie będąca konsekwencją osi niewłaściwej |
grupa typu Cn lub Dn |
W ostatnim przypadku ustalenie pełnego symbolu grupy punktowej wymaga przeprowadzenia następującego rozumowania (gwiazdką oznaczono grupy punktowe rzadkie dla cząsteczek związków chemicznych):
Istnieje oś Cn nie będąca konsekwencją osi niewłaściwej |
|||||
brak osi C2 prostopadłych do osi głównej |
istnieją osie C2 prostopadłe do osi głównej |
||||
istnieje σh (ewentualnie również inne płaszczyzny) |
brak σh, istnieje nσv |
brak płaszczyzn odbicia |
istnieje σh (ewentualnie również inne płaszczyzny) |
brak σh, istnieje nσd |
brak płaszczyzn odbicia |
Cnh * |
Cnv |
Cn |
Dnh |
Dnd |
Dn * |
Spróbujmy określić grupę punktową dla cząsteczki CO2, etenu, anionu cyklopentadienylowego i związku o wzorze WF4Cl2.
1. CO2 jest cząsteczką liniową niepolarną: O=C=O. Skoro wszystkie atomy leżą na jednej prostej, będzie ona zarazem osią główną cząsteczki; obrót o dowolny, nieskończenie mały kąt „odtwarza” początkowe położenie atomów, zatem krotnością tej osi jest nieskończoność. Dalsze rozumowanie odbywa się wg drugiej tabeli: oś C∞ generuje nieskończoną liczbę płaszczyzn σv; oprócz tego - ponieważ cząsteczka jest symetryczna - generuje istnienie nieskończonej liczby osi C2 prostopadłych do osi C∞, czyli grupa jest typu D. Oprócz wymienionych elementów symetrii istnieją w tej cząsteczce środek inwersji i płaszczyzna prostopadła do osi głównej, zatem grupą punktową CO2 jest D∞h.
2. Cząsteczka etenu jest płaska, prostokątna. Skoro wszystkie atomy leżą w jednej płaszczyźnie, będzie ona płaszczyzną symetrii tej cząsteczki. Wszystkie osie symetrii cząsteczki etenu są osiami dwukrotnymi C2, ewentualnie można potraktować oś prostopadłą do płaszczyzny cząsteczki jako główną. W takiej sytuacji płaszczyzna cząsteczki będzie σh. Oprócz niej istnieją w cząsteczce etenu jeszcze dwie płaszczyzny odbicia, przebiegające przez środki przeciwległych boków i środek inwersji, ale niezależnie od tego grupą punktową tej cząsteczki jest D2h.
3. Anion cyklopentadienylowy C5H5- również jest płaski; ma kształt pięciokąta foremnego. Zatem jego osią główną będzie oś C5 przebiegająca przez środek cząsteczki, prostopadle do niej. Płaszczyzna cząsteczki będzie płaszczyzną σh. Oś główna generuje istnienie 5 osi C2 prostopadłych do niej i przebiegających przez jeden z wierzchołków oraz środek przeciwległego boku (a także 5 ułożonych tak samo σv). Zgodnie z tym grupą punktową tego jonu jest D5h.
4. Cząsteczka dichlorku tetrafluorku wolframu może mieć jedną z dwóch możliwych struktur. Atomy chloru mogą leżeć po przeciwległych stronach atomu wolframu (konfiguracja trans) lub po tej samej stronie (konfiguracja cis). Konfiguracja trans ma wyższą symetrię, ponieważ ten wariant cząsteczki zawiera prostą, na której leżą oba atomy Cl i atom W, będącą zarazem osią obrotu C4. Jest to oś główna tej cząsteczki, które generuje istnienie 4 osi C2 (dwie z nich są prostymi, na których leżą dwa atomy F i atom W, dwie pozostałe przechodzą przez środki odległości między przeciwległymi parami atomów fluoru). Ponadto cząsteczka zawiera środek inwersji oraz płaszczyznę odbicia, na której leżą wszystkie atomy fluoru i atom wolframu, prostopadłą do osi głównej, a zatem σh. Grupą punktową trans-WF4Cl2 jest D4h.
W przypadku konfiguracji cis nie występuje oś o tak wysokiej krotności, a liczba elementów symetrii jest znacznie mniejsza. Jedyną osią obrotu jest oś przechodząca przez atom wolframu i środek odległości między atomami chloru - C2. Oś ta nie generuje jednak innych osi, a jedynie dwie płaszczyzny odbicia: jedną przechodzącą przez oba atomy Cl i atom W, a drugą prostopadłą do niej i zawierającą oś C2. Są to więc płaszczyzny σv, a grupą punktową cząsteczki jest C2v.
Symetrię orbitali atomowych i molekularnych również można określać, opisując ich zachowanie względem operacji symetrii. Jest to o tyle przydatne, że symetria jest jednym z kryteriów określania, które orbitale atomowe będą się ze sobą kombinować, dając orbitale molekularne. Kombinują się (efektywnie nakładają) orbitale o analogicznej symetrii, należy jednak pamiętać, że symetria orbitali atomowych silnie zależy od symetrii cząsteczki, którą atomy tworzą. Na przykład w liniowej cząsteczce dwuatomowej trzy orbitale p nie są równocenne: jeden z nich, leżący na osi cząsteczki, ma symetrię σ, a dwa pozostałe, prostopadłe do osi - symetrię π. Z drugiej strony w cząsteczce oktaedrycznej, gdy ligandy znajdują się na osiach układu kartezjańskiego, orbitale p, jako leżące na tych osiach, są równocenne i mają symetrię σ.
Symetrię orbitali atomowych i molekularnych oznacza się tzw. symbolami Mullikena:
Dla pełnego określenia symetrii orbitalu wymagane są jeszcze dalsze oznaczenia (chyba że cząsteczka nie ma żadnych elementów symetrii). Większość orbitali składa się z części dodatniej i ujemnej. Niektóre operacje symetrii mogą zachowywać układ znaków konturów orbitalu (mówimy, że orbital jest symetryczny względem danej operacji), a inne mogą zamieniać plus z minusem i odwrotnie (wtedy orbital jest antysymetryczny względem danej operacji).
Sposób ustalania symbolu symetrii orbitalu opisuje poniższa tabela.
Stopień degeneracji |
|||
niezdegenerowany |
dwukrotnie zdegenerowany |
trzykrotnie zdegenerowany |
|
a lub b |
e |
t |
|
Obrót względem osi głównej |
|||
symetryczny |
antysymetryczny |
||
a |
b |
||
Obrót względem C2 prostopadłej do osi głównej (jeśli jest) lub odbicie względem płaszczyzny σv |
|||
symetryczny |
antysymetryczny |
||
1 |
2 |
||
Odbicie względem płaszczyzny σh (jeśli jest) |
|||
symetryczny |
antysymetryczny |
||
' |
” |
||
Inwersja (jeśli istnieje środek inwersji) |
|||
symetryczny |
antysymetryczny |
||
g |
u |
||
Zgodnie z powyższymi zasadami, orbital s jest zawsze w pełni symetryczny - składa się tylko z części dodatniej, więc żadna operacja symetrii nie może zamienić jego części dodatniej z ujemną. Oznacza się go symbolem a1g/a1'.
Orbital pz w cząsteczce trójkątnej, położonej w płaszczyźnie XY, jest symetryczny wobec obrotu o oś główną (a), antysymetryczny wobec obrotu o oś C2 tej cząsteczki (2) i antysymetryczny wobec odbicia względem σh (”). Oznacza się go więc symbolem a2/a2”.
Podstawowa zasada, wiążąca właściwości związku z jego symetrią, brzmi: im wyższa symetria, tym mniejsza reaktywność. Cząsteczki o wysokiej symetrii są zwykle szczególnie trwałe i mało reaktywne, co jednak nie musi iść w parze. Przyczyną dużej trwałości cząsteczek wysoce symetrycznych jest fakt, że wobec wysokiej symetrii rozkładu gęstości prawdopodobieństwa ich chmura elektronowa nie ma „słabych punktów”, wyróżniających się miejsc, które łatwo byłoby zaatakować. Cząsteczka jest „gładka” wobec ataku reagentów - nie znajdują one punktu zaczepienia i nie mogą się połączyć z daną cząsteczką w celu utworzenia kompleksu aktywnego.
Oczywiście symetria nie jest jedynym czynnikiem wpływającym na reaktywność związku. Istotną rolę odgrywają tutaj także wysycenie walencyjne i koordynacyjne, a także inne czynniki.
Cząsteczka silanu SiH4 ma taką samą budowę, jak cząsteczka metanu - tetraedryczną. Jednak metan jest związkiem wysoce odpornym na działanie czynników zewnętrznych - na przykład nie ulega hydrolizie. Natomiast silan jest związkiem mało trwałym i w środowisku wodnym błyskawicznie hydrolizuje. Jest to spowodowane zarówno niewysyceniem koordynacyjnym atomu Si (krzem, w przeciwieństwie do węgla, ma orbitale d), jak i obecnością w cząsteczce silanu ujemnie spolaryzowanych atomów wodoru, które reagują z dodatnio spolaryzowanymi atomami H z cząsteczek wody.
Do podobnego wniosku prowadzi porównanie właściwości dwuatomowych cząsteczek homojądrowych azotu, tlenu i fluoru. Wszystkie należą do grupy D∞h, jednak cząsteczka azotu jest niezwykle trwała i bierna chemicznie, w przeciwieństwie do cząsteczek tlenu i fluoru. Zróżnicowanie reaktywności wynika z istnienia potrójnego wiązania w cząsteczce N2. O2 zawiera wiązanie podwójne, F2 - pojedyncze, a dodatkowym czynnikiem zwiększającym reaktywność molekularnego tlenu jest obecność w jego cząsteczce dwóch niesparowanych elektronów.
Wysoka symetria cząsteczek zmniejsza rolę oddziaływań międzycząsteczkowych. Cząsteczki wysoce symetryczne są niepolarne, co uniemożliwia powstanie oddziaływań dipol-dipol. Dlatego związki o wysoce symetrycznych cząsteczkach najczęściej tworzą kryształy molekularne, czyli charakteryzują się niskimi temperaturami topnienia i wrzenia oraz łatwością sublimacji.
Zagadnienia dodatkowe
W szkołach średnich i wcześniejszych nierzadko z różnych względów stosuje się uproszczone podejście do wielu problemów chemicznych. O ile na wcześniejszych szczeblach edukacji nie stanowi to wielkiego problemu, o tyle studenci chemii nie powinni się już tymi uproszczeniami posiłkować, ponieważ mogą one powodować błędne rozumienie wielu aspektów chemii.
Najpoważniejszym z tych problemów jest mylenie lub łączenie pojęć stopnia utlenienia i wartościowości. Przyczyną tego stanu rzeczy jest przypisywanie zbytniej uniwersalności strukturalnym wzorom kreskowym, w których kreski mają odzwierciedlać wiązania, a liczba kresek - wartościowość pierwiastka. Powszechnie uczy się rysowania takich wzorów dla wszystkich związków, zapominając, że wzór kreskowy jest wzorem pojedynczej cząsteczki, nie może więc reprezentować związków, które pojedynczych cząsteczek normalnie nie tworzą. Błąd ten dotyczy przede wszystkim soli i związków typu soli, takich jak związki kompleksowe (substancji tworzących jonowe sieci krystaliczne), a także związków, w których sieci krystalicznej występują wiązania koordynacyjne. Zatem:
TAK |
NIE |
Uzasadnienie |
H-Cl |
Na-Cl |
Chlorek sodu tworzy kryształ jonowy, w którym jony Na+ i Cl- występują w proporcji 1:1. Związek ten nie tworzy pojedynczych cząsteczek. |
O=C=O |
O=Ti=O |
Związek ten nie tworzy pojedynczych cząsteczek, a koordynacyjną sieć krystaliczną. LKTi może wynosić na przykład 6 (rutyl). |
|
|
Związek ten nie tworzy pojedynczych cząsteczek, a sieć zawierającą jony K+ i SO42-. |
|
|
Związek ten nie tworzy pojedynczych cząsteczek, a koordynacyjną sieć krystaliczną. LKAl wynosi, w zależności od odmiany, 6 lub 4. |
Cl-Hg-Cl** |
Cl-Zn-Cl |
Związek ten nie tworzy pojedynczych cząsteczek, a koordynacyjną sieć krystaliczną. LKZn wynosi 4. |
* w roztworach rozcieńczonych
** struktura poprawna w roztworze - związek ten nie dysocjuje
Rysowanie poprawnych wzorów kreskowych substancji stałych wymaga uprzedniego zdobycia wiedzy o strukturze krystalicznej danego związku. Niekiedy nawet to nie wystarcza, gdyż może się zdarzyć, że dany związek tworzy kryształ molekularny, ale skład cząsteczek znajdujących się w sieci krystalicznej nie odpowiada najprostszemu wzorowi chemicznemu. Jest tak między innymi w przypadku tlenków fosforu.
Szczególne zagrożenie niesie ze sobą rysowanie wzorów kreskowych związków kompleksowych, na przykład NiCl2·6H2O jako Cl-Ni-Cl (o czym więcej za chwilę). Dlaczego zaś błędny wzór kreskowy jest niebezpieczny? Dlatego, że może posłużyć jako podstawa do określania parametrów tworzących związek atomów, jak na przykład wartościowość.
Bywa, zwłaszcza w gimnazjum, że rysuje się coś takiego:
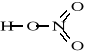
i podpisuje „kwas azotowy(V)”. Uczeń dostrzega zbieżność rzymskiej piątki z „pięcioma” wiązaniami wytworzonymi przez atom azotu i utrwala sobie kwas azotowy(V) jako związek azotu „pięciowartościowego”, podczas gdy jest to związek azotu na V stopniu utlenienia. Absurd ten podejmują nawet niektóre oficjalne wydawnictwa, zwłaszcza nieco starsze.
Zastanówmy się, czym jest wartościowość. Przede wszystkim trzeba zauważyć, że wartościowość powinna być zawsze odnoszona do konkretnego atomu w konkretnym związku, a nie do abstrakcyjnego pierwiastka. Najprostsza definicja mówi, że wartościowość to liczba tworzonych przez atom wiązań. Można je na przykład policzyć, korzystając z prawidłowo narysowanego wzoru kreskowego. Taka definicja wartościowości jest zupełnie wystarczająca w szkołach ponadgimnazjalnych, jednak trzeba zauważyć, że „pewniejsza” jest definicja sformułowana na gruncie teorii orbitali molekularnych: wartościowość to liczba orbitali atomowych danego atomu, które biorą udział w tworzeniu orbitali molekularnych danej cząsteczki. Z natury rzeczy w grę wchodzą tu wyłącznie orbitale walencyjne - orbitale ostatniej powłoki - podobnie, jak w reakcjach chemicznych biorą udział wyłącznie elektrony walencyjne atomów.
Orbitale molekularne są tworzone (według teorii LCAO MO) metodą liniowej kombinacji orbitali atomowych, a liniowa kombinacja ma to do siebie, że liczba powstających orbitali molekularnych równa jest liczbie wziętych do kombinacji orbitali atomowych. Podsumowując: liczba wiązań, a więc i wartościowość pierwiastka, może być maksymalnie równa liczbie jego walencyjnych (bo tylko te biorą udział w tworzeniu wiązań) orbitali atomowych. Azot zaś, mający konfigurację elektronową 1s2 2s2 2p3, ma cztery orbitale walencyjne (2s, 2px, 2py, 2pz) i tyle też wynosi jego maksymalna wartościowość! Piątego wiązania atom azotu nie wytworzy, bo po prostu nie ma z czego. Dotyczy to także pozostałych pierwiastków drugiego okresu. Natomiast atomy pierwiastków dalszych okresów mają do dyspozycji niskoenergetyczne orbitale d, co umożliwia im tworzenie większej liczby wiązań.
Jak w takim razie rysować wzór kwasu azotowego(V)? Istnieją dwa sposoby, z których jeden jest do przyjęcia, a drugi jest absolutnie poprawny:
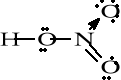
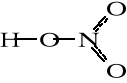
Zastosowanie strzałki wyobrażającej wiązanie kowalencyjne spolaryzowane, które powstaje w mechanizmie donorowo-akceptorowym, może budzić pewne wątpliwości, czy odpowiada ono wiązaniu pojedynczemu (jak w HNO3), czy podwójnemu (jak w H2SO4). Ponadto różnicowanie wiązania donorowo-akceptorowego od „zwykłego” wiązania kowalencyjnego spolaryzowanego nie jest zbyt właściwe, gdyż wiązania te - gdy już powstaną - są całkowicie nierozróżnialne: na przykład jon NH4+ ma strukturę w pełni symetrycznego tetraedru.
Drugi wariant, z kreskami przerywanymi, oznaczającymi wiązanie zdelokalizowane, zapewnia maksymalną zgodność z rzeczywistością, choć oczywiście jego wprowadzenie wymagałoby od uczniów znajomości pojęcia delokalizacji wiązań.
Problem mylenia wartościowości ze stopniem utlenienia wygląda jeszcze gorzej w przypadku związków koordynacyjnych, to znaczy ogromnej większości związków pierwiastków bloku d oraz części związków metali s- i p-elektronowych. Bardzo często mówi się o żelazie trójwartościowym czy miedzi dwuwartościowej - niestety, nawet na wyższych uczelniach, wśród chemików nie będących nieorganikami. Tymczasem wartościowość atomu centralnego w związku koordynacyjnym zależy najczęściej (wyjątkiem jest blok s, którego pierwiastki tworzą bardzo mało typowych związków kompleksowych) od składu wewnętrznej sfery koordynacji: liczby i charakteru ligandów. Sieć krystaliczna związków kompleksowych może mieć budowę:
Zasada o ustalaniu wartościowości metalu centralnego w związku kompleksowym jest banalnie prosta: jeśli ligand tworzy z atomem/jonem centralnym tylko wiązania σ (jak na przykład woda lub amoniak), wartościowość metalu centralnego jest równa liczbie koordynacji. Jeśli ligand tworzy także wiązania π, wartościowość metalu centralnego jest zawsze większa od liczby koordynacji (na przykład dla metali bloku d wynosi 9). Wartościowość atomu/jonu centralnego w związku kompleksowym nigdy nie może być niższa od liczby koordynacji! Analiza przykładowych związków koordynacyjnych zamieszczona jest w tabeli:
Wzór sumaryczny |
Związek zawiera |
Rzeczywista budowa |
Rzeczywista wartościowość |
AlF3 |
Glin(III) „trójwartościowy” |
Sieć koordynacyjna, zawierająca jako jednostkę strukturalną oktaedry AlF6 |
6 |
NiCl2·6H2O |
Nikiel(II) „dwuwartościowy” |
Sieć jonowa, składająca się z kationów kompleksowych [Ni(H2O)6]2+ i anionów Cl- |
6 |
CuSO4·5H2O |
Miedź(II) „dwuwartościową” |
Jony miedzi mają LK=6, jak widać na rysunku. |
6 |
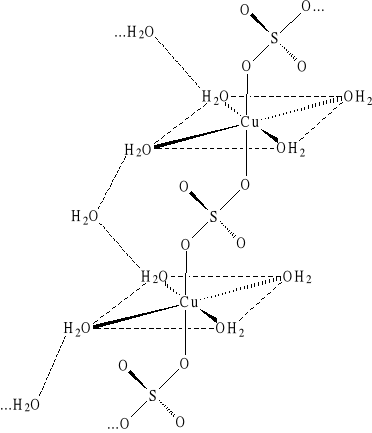
W przypadku związków kompleksowych wartościowość najczęściej nie ma nic wspólnego ze stopniem utlenienia, ponieważ zależy ona jedynie od atomów, z którymi jon centralny łączy się bezpośrednio, to jest tymi, które znajdują się w jego wewnętrznej sferze koordynacji.
Poważne problemy sprawią miłośnikom rysowania wzorów kreskowych związki nieco mniej typowe, o których wspomina się jednak w podręcznikach chemicznych przeznaczonych dla profilu rozszerzonego. Przyjrzyjmy się ponadtlenkom i ozonkom: są to związki zawierające odpowiednio jony O2- i O3-. Tlen tworzy je z najbardziej aktywnymi metalami z grupy litowców (potas, cez, rubid). Czy można narysować wzory strukturalne na przykład KO2 albo RbO3? Zgodnie z tradycyjnym traktowaniem litowców jako metali „jednowartościowych” i tlenu jako zawsze „dwuwartościowego” - nie jest to możliwe w żaden sposób. Dodatkowa wątpliwość pojawia się po obliczeniu stopnia utlenienia tlenu: jest on ułamkowy, wynosi -½ w ponadtlenkach i -1/3 w ozonkach (litowce występują - mając tylko jeden elektron walencyjny - na I stopniu utlenienia). A wartościowość, jako liczba wiązań, powinna być zawsze liczbą naturalną.
To jeszcze nie koniec kłopotów, jakie sprawia tlen osobom utożsamiającym wartościowość ze stopniem utlenienia. Przyjrzyjmy się budowie ozonu - związku, który zyskał ostatnio ogromną medialną popularność. Zmierzony doświadczalnie kąt między wiązaniami w cząsteczce O3 wynosi około 120º, co wskazywałoby na hybrydyzację sp2 centralnego atomu tlenu. W takiej sytuacji atom ten musi być stabilizowany dodatkowym wiązaniem. W cząsteczce ozonu powstaje zatem zdelokalizowane wiązanie π. Wartościowość centralnego atomu tlenu wynosi 3. Ale terminalne atomy tlenu nie tworzą wiązania między sobą; gdyby tworzyły, nie można by ich nazwać terminalnymi, a kąt między wiązaniami musiałby wynosić 60º (jak w trójkącie równobocznym).
TAK |
NIE |
|
|
Kolejny twardy orzech do zgryzienia, uzmysławiający niewłaściwość utożsamiania lub mylenia stopnia utlenienia z wartościowością, to związki na zerowym stopniu utlenienia. Abstrahując od „przyznawanego formalnie” zerowego stopnia utlenienia w niektórych związkach chemicznych (w takiej sytuacji jest na przykład centralny atom węgla w cząsteczce H2C=C=CH2), istnieją pewne związki kompleksowe, w których występują atomy metali na rzeczywistym zerowym stopniu utlenienia. Należą do nich m.in. kompleksy karbonylowe, otrzymywane przez łączenie metalu z tlenkiem węgla, na przykład [Cr(CO)6]. Cząsteczka takiego związku jest elektrycznie obojętna, tak samo jak cząsteczka CO, nie ma więc innego wyjścia, jak tylko przyjąć wynik nieskomplikowanego obliczenia matematycznego: 0 - 0 = 0 i uznać, że chrom występuje na zerowym stopniu utlenienia. Ale przecież tworzy cząsteczkę, więc jego wartościowość nie może wynosić zero, ponieważ oznaczałoby to brak jakichkolwiek wiązań, czyli nieistnienie cząsteczki! Wystarczy przeanalizować budowę tego związku na gruncie teorii VB, by ujrzeć, ile wynosi wartościowość chromu w heksakarbonylchromie(0) - jest równa 9 z uwagi na obecność wiązań π.
Na zakończenie tych przydługich dywagacji wypada napomknąć o czynionych ostatnio próbach przysłowiowego „wyganiania diabła szatanem”, a mianowicie o zastąpieniu pojęcia „wartościowość” liczbą koordynacji, a pojęcia „stopień utlenienia” - tzw. elektrowartościowością. Autor pozwala sobie jednak zadać pytanie: dlaczego jeden dobrze zdefiniowany termin (stopień utlenienia) miały zostać zastąpiony drugim, oznaczającym dokładnie to samo (elektrowartościowość)? Przypomina to podjętą kilka lat temu próbę zastąpienia utleniania dezelektronacją, a redukcji elektronacją (przy czym próba ta była o tyle zasadna, iż nowe terminy zwracały uwagę, że procesy redoksowe są związane z przemieszczaniem elektronów).
Termin „wartościowość” miałby zostać odesłany do lamusa z uwagi na rzekomą nieokreśloność czy nieścisłość definicji. Być może w niektórych źródłach takie nieścisłe definicje się znajduje, cóż jest jednak nieścisłego w stwierdzeniu, iż wartościowość atomu to liczba wytworzonych przezeń wiązań? A jeśli ktoś pragnie większej ścisłości, ma do dyspozycji także przytoczoną powyżej definicję opartą na teorii orbitali molekularnych.
Pomysł zastąpienia wartościowości liczbą koordynacji jest pomysłem w najlepszym razie nieszczęśliwym. Znów należy stanowczo powiedzieć, że przede wszystkim nie jest to to samo! Widać to nie tylko na przykładzie opisywanego przed chwilą związku kompleksowego [Cr(CO)6], gdzie LKCr=6, a wartościowość chromu wynosi 9. Znacznie bardziej oczywistym przykładem jest dobrze znany tlenek węgla(IV). W cząsteczce O=C=O LK atomu węgla wynosi 2, ale jego wartościowość - o czym nikogo nie trzeba przekonywać - jest równa cztery. W wielu cząsteczkach ma miejsce sytuacja, w której inną wartość przyjmuje stopień utlenienia, inną liczba koordynacji, a jeszcze inną - wartościowość. Na przykład w jonie manganianowym(VII), MnO4-, liczba koordynacji manganu jest równa 4, stopień utlenienia manganu wynosi VII, a wartościowość - z uwagi na obecność w cząsteczce czterech wiązań σ i pięciu wiązań π - jest równa 9. Wartościowość i liczba koordynacji to pojęcia opisujące różne parametry cząsteczki, dlatego rezygnacja z któregoś z nich jest nieuzasadniona.
Do najpoważniejszych błędów należy również rysowanie wzorów strukturalnych anionów kwasów tlenowych, uzyskiwanych przez zwykłe „oderwanie” atomów wodoru od cząsteczki odpowiedniego kwasu, na przykład w przypadku anionu siarczanowego(VI):
Wzór ten jest absolutnie nieprawidłowy z co najmniej trzech powodów:
Wobec tego prawidłowy wzór strukturalny jonu siarczanowego(VI) jest następujący:
Należy oczywiście pamiętać o fakcie, że na powyższym rysunku pominięto informację o przestrzennej (tetraedrycznej), a nie płaskiej (kwadratowej) budowie tego jonu. Widoczna jest w każdym razie delokalizacja wiązań π oraz delokalizacja ładunku, zaznaczona przez zapis wartości ładunku poza nawiasem kwadratowym obejmującym cały jon.
Podobne rozumowanie dotyczy też innych anionów kwasów tlenowych, w których występują wiązania π, na przykład:
Delokalizacja wiązań π i ładunku powoduje, że anion kwasowy ma najczęściej wyższą symetrię niż cząsteczka wyjściowego kwasu. Wzrost symetrii można powiązać ze skłonnością kwasu do dysocjowania w odpowiednim środowisku. Jeśli porównać szereg podobnych kwasów, na przykład kwasów chloru na poszczególnych stopniach utlenienia, to moc kwasu jest proporcjonalna do wzrostu symetrii następującego w wyniku dysocjacji. Przyczyną tego faktu jest rola czynnika entropowego, ponieważ zwiększeniu symetrii odpowiada wzrost entropii.
Innym błędem związanym z tym zagadnieniem jest „mieszanie” dwóch wzorów, tj. zaznaczanie delokalizacji ładunku bez uwzględniania delokalizacji wiązań π. W rezultacie otrzymujemy wzór w rodzaju:

Obliczmy jednak, ile elektronów gromadzi atom tlenu, na przykład połączony z siarką podwójnym wiązaniem. Tlen jest pierwiastkiem drugiego okresu i jego atom ma cztery orbitale walencyjne (2s, 2px, 2py, 2pz), może więc mieć w swoim otoczeniu maksymalnie osiem elektronów, bo tyle zmieszczą te orbitale. Tymczasem w powyższym wzorze atom tlenu z grupy S=O ma dwie wolne pary elektronowe oraz dwie uwspólnione z siarką pary tworzące wiązanie σ i π. Wskutek delokalizacji ładunku musiałby jednak przyjąć jeszcze „część” elektronu, ponieważ zdelokalizowane ładunek obejmuje wszystkie atomy tlenu w anionie! Nie może jednak tego zrobić, ponieważ nie ma już wolnych orbitali. Zatem powyższy wzór jest błędny - we wzorach anionów kwasowych delokalizacja ładunku jest nierozerwalnie związana z delokalizacją wiązania π. Dopiero przy delokalizacji obu tych elementów anion kwasowy osiąga swoją maksymalną symetrię.
Mimo iż w nomenklaturze chemicznej kwestia ta została już dość dawno uregulowana, dość często zdarza się nawyk nazywania wodorosoli solami kwaśnymi, a hydroksosoli - solami zasadowymi. Jest to oczywiście niewłaściwe, ponieważ odczyn wodorosoli wcale nie musi być kwasowy, a hydroksosoli - zasadowy. Odczyn wodnego roztworu soli zależy przede wszystkim od faktu, czy w trakcie rozpuszczania tej soli zachodzi wyłącznie dysocjacja, czy również hydroliza.
NaHSO4 ![]()
Na+ + H+aq + SO42-
i powstaje oczywiście odczyn kwasowy. Gdy rozważamy wodorosól mocnego kwasu i słabej zasady, dalsza hydroliza kationu metalu także przyczynia się do zakwaszenia roztworu.
NaHCO3 ![]()
Na+ + HCO3-
HCO3- + H2O ![]()
CO2·H2O + OH-
Jak widać, roztwór takiej wodorosoli ma odczyn zasadowy.
Ba(OH)Cl ![]()
Ba2+ + OH- + Cl-
i powstaje odczyn zasadowy
Cu(OH)Cl ![]()
Cu(OH)+ + Cl-
Cu(OH)+ + H2O ![]()
Cu(OH)2 + H+aq
i powstaje odczyn kwasowy.
Nazywanie karbidu węglikiem bierze się z niedostatecznej skrupulatności w klasyfikowaniu tego związku. Porównajmy związki o wzorach H2O i H2O2. Ten pierwszy można by niewątpliwie nazwać tlenkiem wodoru; drugiego związku „tlenkiem” żaden chemik nie nazwie. To oczywiście nadtlenek wodoru. W tlenkach występuje tlen na -II stopniu utlenienia, a w nadtlenkach - tlen na -I stopniu. Porównajmy teraz związki Ca2C i CaC2. Jeśli ten drugi (karbid) nazwiemy węglikiem, to jak nazwiemy pierwszy? Skoro wapń jest zawsze na II stopniu utlenienia, to węgiel w pierwszym związku występuje na -IV stopniu utlenienia, a w karbidzie - na -I. Jeśli już, to węglikiem można nazwać raczej pierwszy związek, zaś karbid - ewentualnie nadwęglikiem. Nie można tej pary związków zaliczać do tych samych grup, gdyż są one różne. Dowodzą tego chociażby produkty hydrolizy:
Ca2C + 4H2O → 2Ca(OH)2 + CH4↑
CaC2 + 2H2O → Ca(OH)2 + C2H2↑
Związki węgla -IV tworzą w wyniku hydrolizy metan, wobec czego można je nazywać metankami, natomiast związki węgla -I prowadzą do acetylenu, przez co uzasadnione jest nazywanie ich acetylenkami.
Przyczyną powstawania acetylenu podczas hydrolizy karbidu i innych acetylenków jest struktura tych związków. Na przykład acetylenek wapnia ma sieć krystaliczną typu chlorku sodu, zawierającą kationy Ca2+ i aniony C22-, w których atomy węgla połączone są potrójnym wiązaniem, jak w cząsteczce acetylenu.
Pojęcie promocji stosowane jest podczas objaśniania teorii wiązań walencyjnych i analizowania budowy związków za pomocą konfiguracji kratkowych, zwłaszcza w związkach boru, węgla, siarki, których budowa tłumaczona jest hybrydyzacją orbitali atomowych. Wygląda to zatem następująco (na przykładzie węgla):

W rzeczywistości można etap promocji pominąć, gdyż cztery orbitale zhybrydyzowane, wypełnione zgodnie z regułą Hunda, dadzą dokładnie taki sam rezultat:

W istocie „promocja” jest koncepcją czysto teoretyczną, nieszkodliwą, dopóki nie nazywa się jej wzbudzeniem. Wzbudzenie jest bowiem realnym procesem fizycznym, zachodzącym dzięki pochłonięciu przez elektron odpowiedniej energii. Nie można oczekiwać, by jakikolwiek elektron rzeczywiście przeskoczył z podpoziomu 2s na 2p bez dostarczenia mu energii.
Zdarza się, że wzory strukturalne niektórych mniej popularnych związków chemicznych rysowane są „po linii najmniejszego oporu”, tak by pasowały do najprostszych (acz niekiedy zwodniczych) zasad rysowania wzorów kreskowych. Otrzymane w ten sposób wzory strukturalne są jednak często niezgodne z danymi eksperymentalnymi, dotyczącymi struktury lub właściwości chemicznych danego związku. Oto niektóre przykłady:
Związek |
Błędnie |
Prawidłowo |
Uzasadnienie |
N2O |
Tlenek azotu(I)
|
Tlenek azotek azotu(V)
|
Badania strukturalne jednoznacznie wskazują na liniową budowę cząsteczki (hybrydyzacja sp centralnego atomu azotu). |
H3PO3 |
|
|
Analiza chemiczna wykazuje, że kwas ten jest dwuwodorotlenowy, ponadto atom fosforu dąży do wysycenia koordynacyjnego i walencyjnego, a to najlepiej zapewnia hybrydyzacja sp3 atomu fosforu przy LKP=4. |
H3PO2 |
|
|
Analiza chemiczna wykazuje, że kwas ten jest jednowodorotlenowy, ponadto atom fosforu dąży do wysycenia koordynacyjnego i walencyjnego, a to najlepiej zapewnia hybrydyzacja sp3 atomu fosforu przy LKP=4. |
Błędna jest też interpretacja kwasu borowego jako kwasu trójzasadowego, podczas gdy z przebiegu dysocjacji widać, iż kwas ten zachowuje się jak kwas jednozasadowy:
H3BO3 + 2H2O ![]()
[B(OH)4]- + H3O+
Taki przebieg dysocjacji wynika z faktu, że atom boru tworzy trwałe związki, w których występują cztery wiązania: albo z trzema wiązaniami σ i jednym π (jak w BF3), albo z czterema wiązaniami σ (jak w boraksie lub anionie BH4-). Jest to spowodowane dążnością do uzyskania wysycenia nie tylko walencyjnego (zużycie wszystkich elektronów walencyjnych na tworzenie wiązań), ale i koordynacyjnego (zużycie wszystkich orbitali walencyjnych na tworzenie wiązań, zwłaszcza σ). Gdyby kwas borowy miał dysocjować jak inne kwasy, to w powstałym jonie BO33- istniałyby jedynie trzy wiązania σ. Jon ten byłby stabilizowany wiązaniem π, powstałym w mechanizmie donorowo-akceptorowym O→B; stan ten jest jednak mniej trwały od czterech wiązań σ, ponieważ hybrydyzacja sp3 odpowiada wyższej symetrii niż sp2.
Chemia, jako nauka ścisła, wymaga od swoich adeptów jednoznacznego posługiwania się pojęciami dobrze zdefiniowanymi i rozumianymi. Jest to niezbędne, aby dwaj chemicy mogli się dobrze porozumieć. Szczególną rolę odgrywa w tym używanie prawidłowej nomenklatury związków chemicznych. Prawidłowej, to znaczy aktualnej.
Zasady nazewnictwa związków chemicznych są ustalane przez IUPAC (Międzynarodową Unię Chemii Czystej i Stosowanej). Zmiany wprowadzane w tych zasadach mają na celu minimalizację dowolności i umożliwienie nadania wszystkim znanym związkom jednoznacznych i niepowtarzalnych nazw. Zmiany te spotykają się czasem z niechęcią części chemików, gdyż mogą się wydawać nieuzasadnionym utrudnianiem opanowania chemii. Jednak mimo swej niedogodności powodują zwykle większe usystematyzowanie milionów znanych związków chemicznych.
Nazwy i symbole pierwiastków o liczbach atomowych od 1 do 103 są dobrze znane i ustalone od dawna. Warto jedynie zauważyć, że dla izotopów wodoru stosuje się oznaczenia D (deuter 2H) i T (tryt 3T). Ponadto jod (symbol I) i wanad (symbol V) mogą być oznaczane odpowiednio Id i Va, jeśli istnieje możliwość pomylenia ich symboli z cyframi rzymskimi.
Nazwy i symbole pierwiastków o liczbach atomowych od 104 do 109 są, zgodnie z zaleceniem IUPAC (1997), następujące:
Tabela 1. Nazwy pierwiastków 104-109.
Z |
Nazwa |
Symbol |
104 |
rutherford |
Rf |
105 |
dubn |
Db |
106 |
seaborg |
Sg |
107 |
bohr |
Bh |
108 |
has |
Hs |
109 |
meitner |
Mt |
Nazwy nowych pierwiastków o liczbie atomowej większej od 109 są tworzone od liczby atomowej pierwiastka z użyciem następujących liczebników:
0 = nil |
1 = un |
2 = bi |
3 = tri |
4 = kwad |
5 = pent |
6 = heks |
7 = sept |
8 = okt |
9 = enn |
Utworzona w ten sposób nazwa hipotetycznego pierwiastka 139 brzmiałaby:
Symbole nowych pierwiastków tworzy się biorąc pierwsze litery trzech liczebników składających się na nazwę pierwiastka (w powyższym przykładzie: untrienn ≡ Ute).
Zgodnie z tą zasadą nazwy znanych pierwiastków o Z>109 są następujące:
Tabela 2. Nazwy istniejących pierwiastków 110-118.
Z |
Nazwa |
Symbol |
110 |
ununnil |
Uuo |
111 |
ununun |
Uuu |
112 |
ununbi |
Uub |
114 |
ununkwad |
Uuq |
116 |
ununheks |
Uuh |
118 |
ununokt |
Uuo |
Wieloatomowe cząsteczki pierwiastków nazywa się z użyciem nazw pierwiastków i odpowiednich liczebników, na przykład N2 - diazot, O2 - ditlen, O3 - tritlen, S8 - oktasiarka.
Terminy jon/kation oraz jon/anion stosuje się zamiennie. Nazewnictwo jonów kompleksowych zostało omówione wraz z nomenklaturą związków kompleksowych.
Fe3+ - kation żelaza(III), jon żelaza(3+)
Hg22+ - kation dirtęci(I), jon dirtęci(2+)
O2+ - jon dioksonylu, kation dioksygenylu
H3O+ - jon oksoniowy lub oksonium
NH4+ - jon amonowy, amonium, azanium
PH4+ - jon fosfoniowy, fosfonium
NO+ - kation nitrozylu
NO2+ - kation nitroilu
SO2+ - kation sulfinylu
SO22+ - kation sulfonylu
BiO+ - kation oksobizmutu(III), dopuszczalnie: kation bizmutylowy(III), kation bizmutylu(1+)
VO2+ - kation oksowanadu(IV), dopuszczalnie: kation wanadylowy(IV)
VO2+ - kation dioksowanadu(V), dopuszczalnie: kation wanadylowy(V)
UO22+ - kation dioksouranu(VI), dopuszczalnie: kation uranylowy(VI)
Poniższe nazwy dotyczą jonów nie będących ligandami w cząsteczce związku kompleksowego.
H- - jon wodorkowy
OH- - anion wodorotlenkowy
S2- - jon siarczkowy
S22- - jon disiarczkowy
C4- - jon węglikowy
C22- - jon diwęglikowy(-I), jon diwęglikowy(2-), dopuszczalnie: jon acetylenkowy
C5H5- - jon cyklopentadienylowy, anion cyklopentadienidowy
O2- - jon ditlenkowy (1-), dopuszczalnie: anion ponadtlenkowy
O22- - jon ditlenkowy (2-), dopuszczalnie: anion nadtlenkowy
O3- - jon tritlenkowy (1-), dopuszczalnie: anion ozonkowy
N3- - jon azotkowy(-III), jon azotkowy(3-)
N3- - jon triazotkowy (1-), dopuszczalnie: anion azydkowy
ClO4- - jon chloranowy(VII), jon tetraoksochloranowy(1-)
HSO3- - jon wodorosiarczanowy(IV)
CH3COO- - jon octanowy, anion etanianowy
Związki binarne to związki, których cząsteczki zawierają atomy tylko dwóch pierwiastków (taka cząsteczka nie musi składać się z dwóch atomów!). We wzorze związku binarnego na pierwszym miejscu umieszcza się symbol pierwiastka zajmującego wcześniejszą pozycję w szeregu:
Rn, Xe, Kr, B, Si, C, Sb, As, P, N, H, Te, Se, S, At, I, Br, Cl, O, F.
Nazwę związku tworzy się, jak wspomniano wcześniej, podając pierwiastki w odwrotnej kolejności. Do nazwy składnika bardziej elektroujemnego dodaje się końcówkę „-ek” lub „-ik”.
PbS2 - siarczek ołowiu(IV)
OF2 - fluorek tlenu(II)
FeN - azotek żelaza(III)
Al4C3 - węglik glinu
W przypadku złożonych związków binarnych pierwiastki wymienia się grupami: najpierw bardziej elektroujemne zgodnie z odwróconym powyższym szeregiem, a potem mniej elektroujemne zgodnie z odwróconym powyższym szeregiem:
N2O (właściwie z uwagi na strukturę cząsteczki: NNO) - tlenek azotek azotu(V).
Ta grupa związków jest powszechnie zwana wodorkami, formalnie jednak wodorkiem możemy nazwać tylko taki związek, w którym wodór jest spolaryzowany ujemnie - czyli związek wodoru z pierwiastkiem o elektroujemności niższej niż elektroujemność wodoru. Należą do nich wszystkie pierwiastki grup 1÷13, lantanowce i aktynowce oraz Si, Ge, Sn, Pb, P, Sb, Bi, Te, Po i At. W przypadku, gdy dany pierwiastek wykazuje identyczną elektroujemność, jak wodór, przyjmuje się, że elektrony tworzące wiązanie znajdują się bliżej atomu o większej liczbie atomowej i atom wodoru przyjmuje polaryzację dodatnią.
NaH - wodorek sodu
MgH2 - wodorek magnezu
Należy zauważyć, że związki większości metali bloku d i f z wodorem mogą mieć skład niestechiometryczny, a wodór nie zawsze jest w nich połączony z atomami metalu zwykłym wiązaniem. W takich przypadkach może on przybierać różną polaryzację, zależną od struktury krystaliczne danego związku, a nie od różnicy elektroujemności między wodorem a metalem. Natomiast nazwy lotnych związków wodoru z pierwiastkami grup 14÷17 tworzy się w inny sposób:
Tabela 3. Nazwy związków wodoru z pierwiastkami grup 14-16.
Wzór |
Nazwa systematyczna |
Nazwa dopuszczalna |
SiH4 |
silan |
|
NH3 |
azan |
amoniak* |
N2H4 |
diazan |
hydrazyna* |
PH3 |
fosfan |
fosfina |
AsH3 |
arsan |
arsyna |
H2O |
oksydan |
woda* |
H2S |
sulfan |
siarkowodór* |
H2Se |
selan |
selenowodór* |
H2Te |
tellan |
tellurowodór* |
* nazwa zalecana
HF - fluorek wodoru
HCl - chlorek wodoru
HBr - bromek wodoru
HI - jodek wodoru
B2H6 - diboran(6) lub diborowodór(6)
B10H14 - dekaboran(14) dub dekaborowodór(14)
W ogromnej większości związków chemicznych tlen występuje na -II stopniu utlenienia (oprócz tlenków należą tu kwasy tlenowe, wodorotlenki, hydroksosole oraz sole i wodorosole kwasów tlenowych). Nazwy tlenków, w których tlen stanowi zawsze pierwiastek bardziej elektroujemny, tworzy się zgodnie z nomenklaturą innych związków binarnych, łącząc słowo „tlenek” z nazwą pierwiastka w dopełniaczu. W razie potrzeby podaje się też stopień utlenienia tego pierwiastka:
BaO - tlenek baru
SiO2 - tlenek krzemu
WO3 - tlenek wolframu(VI)
Cl2O7 - tlenek chloru(VII)
Powyższe przykłady dotyczą tlenków prostych. Znane są również tlenki podwójne (potrójne itd.):
Pb3O4 ≡ Pb2PbO4 ≡ PbO2·2PbO - tlenek diołowiu(II) ołowiu(IV)
Fe3O4 ≡ Fe2O3·FeO - tlenek żelaza(II) diżelaza(III)
MgWO4 ≡ MgO·WO3 - tetratlenek magnezu wolframu(VI)
FeNiO4 ≡ Fe2O3·NiO - tetratlenek niklu(II) diżelaza(III).
Ponadto tlen tworzy następujące związki:
H2O2 - nadtlenek wodoru
BaO2 - nadtlenek baru;
RbO2 - ponadtlenek rubidu
Ba(O2)2 - ponadtlenek baru
CsO3 - ozonek cezu;
IV: O3 - ozon (tritlen, formalnie można by go nazwać tlenkiem tlenu(IV))
II: OF2 - fluorek tlenu(II)
I: O2F2 - difluorek ditlenu(I)
½: O2[AsF6] - heksafluoroarsenian(V) dioksygenylu
Nazwy anionów kwasów beztlenowych mają charakterystyczną końcówkę „-kowy”, a soli tych kwasów „-ek”.
Tabela 4. Nazwy kwasów beztlenowych i ich pochodnych.
Wzór kwasu |
Nazwa systematyczna |
Nazwa dopuszczalna |
Nazwa anionu |
Nazwa soli |
HF |
fluorek wodoru |
kwas fluorowodorowy |
anion fluorkowy |
fluorek |
HCl |
chlorek wodoru |
kwas chlorowodorowy |
anion chlorkowy |
chlorek |
HBr |
bromek wodoru |
kwas bromowodorowy |
anion bromkowy |
bromek |
HI |
jodek wodoru |
kwas jodowodorowy |
anion jodkowy |
jodek |
H2S |
siarczek diwodoru |
kwas siarkowodorowy |
anion siarczkowy |
siarczek |
H2S2 |
disiarczek diwodoru |
|
anion disiarczkowy |
disiarczek |
H2Se |
selenek wodoru |
|
anion selenkowy |
selenek |
HCN |
cyjanek wodoru |
kwas cyjanowodorowy |
anion cyjankowy |
cyjanek |
HNCO |
izonitrydooksowęglan wodoru |
kwas izocyjanowy |
anion izocyjanowy |
izocyjanian |
HN3 |
azydek wodoru |
kwas azotowodorowy |
anion azydkowy |
azydek |
Nazwy kwasów tlenowych mają charakterystyczną końcówkę „-owy”, nazwy ich anionów „-anowy”, zaś nazwy soli tych kwasów „-an”. Jeśli dany pierwiastek tworzy kwasy na więcej niż jednym stopniu utlenienia (na przykład chlor - na I, III, V, VII), podaje się ten stopień zgodnie z systemem Stocka. Różnice stosunku molowego tlenku kwasowego i wody wyraża się przedrostkami meta- (mniejszy stopień uwodnienia) i orto- (większy stopień uwodnienia). Niedozwolone jest natomiast stosowanie przedrostków nad- i pod- oraz końcówki -awy (w przypadku nazwy anionu lub soli -końcówki -yn).
Tabela 5. Nazwy kwasów tlenowych i ich soli.
wzór kwasu |
nazwa w systemie Stocka |
nazwa soli* |
H3AsO3 |
kwas arsenowy(III) |
arsenian(III) (anion arsenianowy(III)) |
H3AsO4 |
kwas arsenowy(V) |
arsenian(V) |
HNO2 |
kwas azotowy(III) |
azotan(III) |
HNO3 |
kwas azotowy(V) |
azotan(V) |
(HBO2)n |
kwas metaborowy |
metaboran |
H3BO3 |
kwas ortoborowy |
ortoboran |
HClO |
kwas chlorowy(I) |
chloran(I) |
HClO2 |
kwas chlorowy(III) |
chloran(III) |
HClO3 |
kwas chlorowy(V) |
chloran(V) |
HClO4 |
kwas chlorowy(VII) |
chloran(VII) |
H2CrO4 |
kwas chromowy(VI) |
chromian(VI) |
H2Cr2O7 |
kwas dichromowy(VI) |
dichromian(VI) |
H3PO3 (H2PHO3) |
kwas fosforowy(III) |
fosforan(III) |
(HPO3)n |
kwas metafosforowy(V) |
metafosforan(V) |
H3PO4 |
kwas (orto)fosforowy(V) |
(orto)fosforan(V) |
H4P2O7 |
kwas difosforowy(V) |
difosforan(V) |
HIO4 |
kwas (meta)jodowy(VII) |
(meta)jodan(VII) |
H5IO6 |
kwas ortojodowy(VII) |
ortojodan(VII) |
H4SiO4 |
kwas ortokrzemowy |
ortokrzemian |
(H2SiO3)n |
kwas metakrzemowy |
metakrzemian |
HMnO4 |
kwas manganowy(VII) |
manganian(VII) |
H2MnO4 |
kwas manganowy(VI) |
manganian(VI) |
H2SO3 |
kwas siarkowy(IV) |
siarczan(IV) |
H2SO4 |
kwas siarkowy(VI) |
siarczan(VI) |
H2S2O7 |
kwas disiarkowy(VI) |
disiarczan(VI) |
H2S2O8 |
kwas peroksodisiarkowy(VI) |
peroksodisiarczan(VI) |
H2S2O3 |
kwas tiosiarkowy(VI) |
tiosiarczan(VI) |
H2CO3 |
kwas węglowy |
węglan |
HOCN |
kwas cyjanowy |
cyjanian |
HNCO** |
kwas izocyjanowy |
izocyjanian |
* W przypadku kwasów wieloprotonowych obecne są również aniony zawierające kationy wodorowe; przykład: HSO4- - anion wodorosiarczanowy(VI); sól - wodorosiarczan(VI)
** Kwas izocyjanowy nie jest oksokwasem, gdyż atom wodoru nie jest związany bezpośrednio z atomem tlenu
Jedną z nowszych propozycji nomenklaturowych IUPAC jest traktowanie kwasów o złożonych anionach jako związków kompleksowych, najczęściej z ligandem tlenkowym (okso). Istnieją tutaj dwa warianty nomenklatury, bardziej tradycyjna nomenklatura kwasowa oraz zalecana tzw. nomenklatura wodorowa.
Nazwa zgodna z nomenklaturą kwasową składa się ze słowa „kwas” oraz słowa identyfikującego anion. Składa się ono z czterech części:
Przykładowo kwasy jodu będą nosić nazwy:
HIO3 - kwas trioksojodowy(V)
HIO4 - kwas tetraoksojodowy(VII)
H5IO6 - kwas heksaoksojodowy(VII)
Nomenklatura kwasowa ma zastosowanie ograniczone w zasadzie wyłącznie do kwasów wymienionych w tabeli na końcu podrozdziału.
Drugi wariant - nomenklatura wodorowa - jest zgodny z obecnym trendem nomenklaturowym, którego celem jest eliminacja nazw odwołujących się do charakteru właściwości chemicznych związku (takich jak kwas czy bezwodnik). Nazwa związku powinna opisywać jego skład i strukturę
Zgodnie z nomenklaturą wodorową kwasy traktuje się jako sole wodoru. Nazwa kwasu w tym ujęciu składa się z dwóch słów, przy czym istnieją tu dwa warianty:
Pierwsze słowo |
||
|
||
|
||
|
|
|
Drugie słowo |
„wodoru” |
„wodoru” poprzedzone przedrostkiem liczbowym, wyrażającym liczbę atomów wodoru |
Tabela 6. Przykładowe nazwy kwasów według nomenklatury wodorowej.
Wzór |
Wariant 1. |
Wariant 2. |
HNO2 |
dioksoazotan(III) wodoru lub |
dioksoazotan (mono)wodoru |
HNO3 |
trioksoazotan(V) wodoru lub |
trioksoazotan (mono)wodoru |
H2SO4 |
tetraoksosiarczan(VI) wodoru lub tetraoksosiarczan(2-) wodoru |
tetraoksosiarczan diwodoru |
H2S2O3 |
trioksotiosiarczan(VI) wodoru lub trioksotiosiarczan(2-) wodoru |
trioksotiosiarczan diwodoru |
H3PO3 (H2PHO3) |
hydrydotrioksofosforan(III) wodoru lub hydrydotrioksofosforan(2-) wodoru |
hydrydotrioksofosforan diwodoru |
Więcej przykładów wraz z nazwami anionów znajduje się w tabeli 7. na końcu rozdziału.
Przykłady nazw kompleksowych kwasów beztlenowych:
H[B(C6H5)4] - tetrafenyloboran wodoru
H2[SiF6] - heksafluorokrzemian diwodoru lub heksafluorokrzemian(2-) wodoru, ewentualnie kwas heksafluorokrzemowy
H[PF6] - heksafluorofosforan(V) wodoru, ewentualnie kwas heksafluorofosforowy(V)
H[AuCl4] - tetrachlorozłocian(III) wodoru, ewentualnie kwas tetrachlorozłotowy(III)
H2[Pt(CN)4] - tetracyjanoplatynian(IV) diwodoru lub tetracyjanoplatynian(2-) wodoru, ewentualnie kwas tetracyjanoplatynowy(IV)
Nazwy oksokwasów wg nomenklatury kwasowej i wodorowej prezentuje tabela 7.
Tabela 7. Nazwy wybranych kwasów tlenowycha według nomenklatury wodorowej i kwasowej.
Wzór |
Nomenklatura wodorowa |
Nomenklatura kwasowac |
Dopuszczalna nazwa kwasu |
Dopuszczalna nazwa anionu |
H3BO3 |
trioksoboran triwodoru |
kwas trioksoborowy |
kwas borowy |
boran |
(HBO2)n |
poli[dioksoboran wodoru] |
kwas polidioksoborowy |
|
|
H2B2(O2)2(OH)4 |
di-μ-perokso-tetrahydroksodiboran diwodoru |
kwas di-(μ-per-okso)-tetrahydrokso-diborowy(2-) |
|
|
H4SiO4 |
tetraoksokrzemian tetrawodoru |
kwas tetraoksokrzemowy |
|
|
(H2SiO3)n |
poli(trioksokrzemian diwodoru) |
kwas politrioksokrzemowy |
|
|
H2CO3 |
trioksowęglan diwodoru |
kwas trioksowęglowy |
kwas węglowy |
węglan |
HOCNb |
nitrydooksowęglan wodoru |
kwas nitrydooksowęglowy(1-) |
kwas cyjanowy |
cyjanian |
HONC |
karbidooksoazotan wodoru |
kwas karbidooksoazotowy(1-) |
kwas piorunowy |
piorunian |
H2N2O2 |
dioksodiazotan(N--N) diwodoru |
kwas dioksodiazotowy(N--N)(2-) |
|
azotan(V) |
HNO2 |
dioksoazotan wodoru |
kwas dioksoazotowy(III) |
kwas azotowy(III) |
azotan(III) |
HNO3 |
trioksoazotan wodoru |
kwas trioksoazotowy(V) |
kwas azotowy(V) |
|
HNO4 |
dioksoperoksoazotan wodoru |
kwas dioksoperoksoazotowy(V) |
|
|
H3PO2 (HPH2O2) |
dihydrydodioksofosforan wodoru |
kwas dihydrydodioksofosforowy(1-) |
kwas fosforowy(I) |
fosforan(I) |
H3PO3 (H2PHO3) |
trioksofosforan triwodoru (hydrydotrioksofosforan diwodoru) |
kwas trioksofosforowy(2-) (kwas hydrydotrioksofosforowy(2-)) |
kwas ortofosforowy(III) |
ortofosforan(III) |
H4P2O5 |
μ-okso-tetraoksodifosforan tetrawodoru |
kwas μ-okso-tetraoksodifosforowy(III) |
|
|
H3PO4 |
tetraoksofosforan triwodoru |
kwas tetraoksofosforowy(V) |
kwas ortofosforowy(V) |
ortofosforan(V) |
H4P2O7 |
μ-okso-heksaoksodifosforan tetrawodoru |
kwas μ-okso-heksaoksodifosforowy(V) |
kwas difosforowy(V) |
difosforan(V) |
(HPO3)n |
poli[trioksofosforan wodoru] |
kwas politrioksofosforowy(V) |
|
|
(OH)2OPPO(OH)2, czyli H4P2O6 |
heksaoksodifosforan(P—P) tetrawodoru |
kwas heksaoksodifosforowy(4-) |
|
|
H3AsO4 |
tetraoksoarsenian triwodoru |
kwas tetraoksoarsenowy(V) |
kwas arsenowy(V) |
arsenian(V) |
H3AsO3 |
trioksoarsenian triwodoru |
kwas trioksoarsenowy(III) |
kwas arsenowy(III) |
arsenian(III) |
H2SO4 |
tetraoksosiarczan diwodoru |
kwas tetraoksosiarkowy(VI) |
kwas siarkowy(VI) |
siarczan(VI) |
HSO3F |
fluorotrioksosiarczan wodoru |
kwas fluorotrioksosiarkowy(1-) |
|
|
H2S2O5 czyli H2SO3(O2) |
trioksoperoksosiarczan diwodoru |
kwas trioksoperoksosiarkowy(2-) |
|
|
H2S2O8 |
μ-perokso-heksaoksodisiarczan diwodoru |
kwas μ-perokso-heksaoksodisiarkowy(VI) |
|
|
H2S2O3 |
trioksotiosiarczan diwodoru |
kwas trioksotiosiarkowy(2-) |
kwas tiosiarkowy(VI) |
tiosiarczan(VI) |
H2S2O7 |
μ-okso-heksaoksodisiarczan diwodoru |
kwas μ-okso-heksaoksodisiarkowy(VI) |
kwas disiarkowy(VI) |
disiarczan(VI) |
H2S3O10 |
di-μ-okso-oktaoksotrisiarczan diwodoru |
kwas di-μ-okso-oktaoksotrisiarkowy(VI) |
|
|
H2SO4·nSO3 |
poli-μ-okso-polioksopolisiarczan diwodoru |
kwas poli-μ-okso-polioksopolisiarkowy(VI) |
|
|
H2S2O5 |
μ-okso-tetraoksodisiarczan diwodoru |
kwas μ-okso-tetraoksodisiarkowy(IV) |
kwas disiarkowy(IV) |
disiarczan(IV) |
H2S2O6 |
heksaoksodisiarczan(S—S) diwodoru |
kwas heksaoksodisiarkowy(2-) |
kwas ditionowy |
ditionian |
H2S3O6 |
heksaoksotrisiarczan(S—S) diwodoru |
kwas heksaoksotrisiarkowy(2-) |
|
|
H2S4O6 |
heksaoksotetrasiarczan(S—S) diwodoru |
kwas heksaoksotetrasiarkowy(2-) |
|
|
H2S2O4 |
tetraoksodisiarczan(S—S) diwodoru |
kwas tetraoksodisiarkowy(2-) |
|
|
H2SO3 |
trioksosiarczan diwodoru |
kwas trioksosiarkowy(IV) |
kwas siarkowy(IV) |
siarczan(IV) |
H2CrO4 |
|
kwas tetraoksochromowy(VI) |
kwas chromowy(VI) |
chromian(VI) |
H2Cr2O7 |
|
kwas μ-okso-heksaoksodichromowy(VI) |
kwas dichromowy(VI) |
dichromian(VI) |
HClOd |
oksochloran wodoru |
kwas oksochlorowy(I) |
kwas chlorowy(I) |
chloran(I) |
HClO2d |
dioksochloran wodoru |
kwas dioksochlorowy(III) |
kwas chlorowy(III) |
chloran(III) |
HClO3d |
trioksochloran wodoru |
kwas trioksochlorowy(V) |
kwas chlorowy(V) |
chloran(V) |
HClO4d |
tetraoksochloran wodoru |
kwas tetraoksochlorowy(VII) |
kwas chlorowy(VII) |
chloran(VII) |
HIO3 |
trioksojodan wodoru |
kwas trioksojodowy(V) |
kwas jodowy(V) |
jodan(V) |
HIO4 |
tetraoksojodan wodoru |
kwas tetraoksojodowy(VII) |
|
|
H5IO6 |
heksaoksojodan pentawodoru |
kwas heksaoksojodowy(5-) |
|
|
HMnO4 |
|
kwas tetraoksomanganowy(1-) |
kwas manganowy(VII) |
manganian(VII) |
H2MnO4 |
|
kwas tetraoksomanganowy(2-) |
kwas manganowy(VII) |
manganian(VII) |
H3P3O9 |
cyklo-trifosforan triwodoru |
|
|
|
H6Mo7O19 |
heptamolibdenian heksawodoru |
|
|
|
H4SiW12O40 |
heksatriakontaokso(tetraoksokrzemiano)dodekawolframian tetrawodoru |
|
|
|
H6P2W18O62 |
tetrapentakontaoksobis(tetraoksofosforano)oktadekawolframian heksawodoru |
|
|
|
a Występowanie nazwy „kwas” w powyższym zestawieniu niekoniecznie oznacza, że dany związek został wyizolowany. Na przykład kwas węglowy nie został dotąd otrzymany w postaci czystego związku, lecz węglany są dobrze znane. Związki takie wymieniono dla zilustrowania metody nomenklatury.
b Kwas izocyjanowy o wzorze HNCO nie jest kwasem tlenowym, ponieważ wodór nic jest w mm związany bezpośrednio z atomem tlenu.
c Podano stopień utlenienia pierwiastka „centralnego” (system Stocka) lub ładunek anionu kwasowego (system Ewansa-Bassetta).
d Znany jest kwas bromu o analogicznej cząsteczce i nazwie.
Nazwy wodorotlenków prostych, tworzy się łącząc słowo „wodorotlenek” z nazwą pierwiastka w dopełniaczu. W razie potrzeby podaje się też stopień utlenienia tego pierwiastka:
Ba(OH)2 - wodorotlenek baru
Fe(OH)3 - wodorotlenek żelaza(III)
Nazwy wodorotlenków złożonych tworzy się, podając poszczególne elementy związku w grupach - najpierw anionowe (bardziej elektroujemne) w kolejności alfabetycznej, a potem kationowe (mniej elektroujemne) w kolejności alfabetycznej, na przykład:
AlO(OH) - tlenek wodorotlenek glinu
W razie potrzeby podaje się też stopnie utlenienia pierwiastków.
Sól jest związkiem składającym się z części kationowej (która może obejmować wodór kwasowy) i części anionowej (mogącej zawierać jony wodorotlenkowe). Tworząc nazwy soli, słowa „jon”, „kation” i „anion” pomija się. Uwaga: w przypadku soli kwasów organicznych obowiązuje obecnie stosowanie się do konwencji „najpierw kation, potem anion”, co wymusza zapis NaCH3CO2 zamiast dawnego CH3COONa!
Sole proste zawierają tylko jeden rodzaj kationu (bez H+aq) i jeden rodzaj anionu (bez OH-).
Sole kwasów beztlenowych nazywa się zgodnie z podanymi wcześniej zasadami nazewnictwa związków binarnych:
NaCl - chlorek sodu
K2S - siarczek potasu
Cu(N3)2 - azydek miedzi(II) lub azydek miedzi(2+)
Podawanie stopni utlenienia jest szczególnie istotne, ponieważ istnieją różne sole o jednakowym wzorze sumarycznym, na przykład:
Tl(I3) - trijodek talu(I) lub trijodek talu(1+)
TlI3 - jodek talu(III) lub trijodek talu lub jodek talu(3+)
Nazwy soli kwasów tlenowych składają się z nazwy anionu kwasowego (tworzonej wg zasad podanych w podrozdziale 2.5.1.2. lub 2.5.1.3.), po której następuje nazwa kationu lub pierwiastka pełniącego rolę kationu:
CaCO3 - węglan wapnia lub trioksowęglan wapnia
CuSO4 - siarczan(VI) miedzi(II) lub tetraoksosiarczan(VI) miedzi(II)
(NH4)3PO4 - ortofosforan(V) amonu lub tetraoksofosforan(V) amonu
Woda hydratacyjna może być związana w sieci krystalicznej na różne sposoby. Może wchodzić w skład sfery koordynacyjnej kationu lub kationów (nazewnictwo takich związków zostanie bardziej szczegółowo omówione w podrozdziale 2.6.), może być związana z anionami lub kationami za pośrednictwem wiązań wodorowych, może wreszcie występować w lukach sieci krystalicznej. Tworząc nazwę soli uwodnionej na ogół nie rozpatruje się sposobu wiązania wody.
Nazwy soli uwodnionych można tworzyć na dwa sposoby:
CuSO4·5H2O - siarczan(VI) miedzi(II)---woda(1/5)
CaCl2·6H2O - chlorek wapnia---woda(1/6)
2CaSO4·H2O - siarczan(VI) wapnia---woda(2/1)
CuSO4·5H2O - pentahydrat siarczanu(VI) miedzi(II)
CaCl2·2H2O - dihydrat chlorku wapnia
Drugi sposób tworzenia nazwy jest jedyny, jeśli sól zawiera niestechiometryczną lub nie określoną dokładnie liczbę cząsteczek wody (nH2O).
Wodorosole to związki zawierające wodór kwasowy, czyli będące na przykład produktem niecałkowitego zobojętnienia kwasu. Uwaga: istnieją kwasy, których cząsteczki zawierają atomy wodoru połączone bezpośrednio z atomem niemetalu (na przykład H3PO3≡H2PHO3, H3PO2≡HPH2O2) - sól takiego kwasu nie jest wodorosolą, jeśli nie zawiera grupy -O-H!
Nazwy wodorosoli tworzy się przez dodanie do nazwy odpowiedniego anionu przedrostka „wodoro” z odpowiednim przedrostkiem liczbowym, na przykład:
KHSO4 - wodorosiarczan(VI) potasu lub wodorotetraoksosiarczan(1-) potasu
NaH2PO4 - diwodoroortofosforan(V) sodu lub diwodorotetraoksofosforan(V) sodu
LiH2PO3 ≡ LiHPHO3 - wodorohydrydotrioksofosforan(III) litu
Tworząc nazwy bardziej skomplikowanych soli, najpierw wymienia się nazwy wszystkich anionów (w kolejności alfabetycznej), a potem nazwy wszystkich kationów (w kolejności alfabetycznej). Wodór wymienia się na końcu jako kation (zwłaszcza gdy jego sposób wiązania nie jest znany), chyba że należy zaznaczyć, iż stanowi on część anionu. W razie potrzeby uwzględnia się odpowiednie przedrostki liczbowe (dla anionów - bis, tris, tetrakis itd.). Na przykład sole zawierające więcej niż jeden kation (także kompleksowy):
KNaCO3 - węglan potasu sodu
AlK(SO4)2·12H2O - siarczan(VI) glinu potasu---woda(1/12)
MgNH4PO4·6H2O - heksahydrat tetraoksofosforanu(V) amonu magnezu
Na(UO2)3[Zn(H2O)6](CH3CO2)9 - nonaoctan heksaakwacynku sodu triuranylu(VI)
Sole zawierające więcej niż jeden anion:
Ca5F(PO4)3 - fluorek tris(ortofosforan(V)) pentawapnia
KBr·KF·2KHSO4 ≡ K4BrF(HSO4)2 - bromek fluorek bis(wodorosiarczan(VI)) tetrapotasu
Sole tlenowe (oksosole) z punktu widzenia nomenklatury są uważane za sole podwójne zawierające anion O2-. Tworząc ich nazwy, należy wymieniać wszystkie nazwy poszczególnych anionów (nie jako ligandów), unikając formy „okso”. Ponadto obowiązują zasady podane w podrozdziade 2.5.3.4.
BiOI - jodek tlenek bizmutu(III)
VOSO4 - siarczan(VI) tlenek wanadu(IV)
ZrCl2(O)·8H2O - oktahydrat dichlorku tlenku cyrkonu
Sole wodorotlenowe (hydroksosole) z punktu widzenia nomenklatury są uważane za sole podwójne zawierające anion OH-. Ponadto przy tworzeniu nazw takich soli obowiązują zasady podane w podrozdziale 2.5.3.4.
CaCl(OH) - chlorek wodorotlenek magnezu
(CuOH)2CO3 ≡ Cu(OH)2·CuCO3 - węglan diwodorotlenek dimiedzi(II)
Zasady nazewnictwa złożonych tlenków zostały podane w podrozdziale 2.4.2. W przypadku nazw wodorotlenków złożonych obowiązują zasady umówione w rozdziale 2.5.3. Niekiedy przy nazwie systematycznej podaje się typ struktury krystalicznej. Przykłady:
Ca3[Al(OH)6]2 - bis(heksahydroksoglinian) triwapnia (nazwa utworzona zgodnie z zasadami nomenklatury związków kompleksowych, patrz rozdział 2.6.)
AlCa2(OH)7·nH2O - hydrat heptawodorotlenku glinu diwapnia
W tradycyjnym ujęciu przedmiotem zainteresowania chemii koordynacyjnej są związki „zawierające” wiele wiązań koordynacyjnych, czyli donorowo-akceptorowych. Wiemy jednak, że wiązania takie są w istocie nieodróżnialne od zwykłych wiązań kowalencyjnych spolaryzowanych, a pojęcie „donorowo-akceptorowe” określa jedynie mechanizm ich powstawania. Zgodnie z formalizmem chemii koordynacyjnej można więc opisywać również związki z wiązaniami kowalencyjnymi spolaryzowanymi, powstającymi w zwykłym mechanizmie, zgodnie z którym każdy z atomów wnosi do wiązania po jednym elektronie.
Prawidłowa definicja związku kompleksowego (koordynacyjnego) brzmi: związek, w którego strukturze cząsteczkowej lub krystalicznej można wyróżnić tzw. jednostki koordynacyjne.
Jednostka koordynacyjna jest strukturą składającą się z atomu lub jonu centralnego (najczęściej kationu metalu, ale czasem także niemetalu, a niekiedy w ogóle obojętnego atomu) i ligandów. Granice jednostki koordynacyjnej, czyli tzw. wewnętrzną sferę koordynacji, zaznacza się we wzorach (zwłaszcza sumarycznych) nawiasem kwadratowym. Jednostka koordynacyjna może być kationem, anionem lub cząsteczką elektrycznie obojętną.
Ligand to jon prosty, złożony lub polarna cząsteczka, który łączy się z atomem/jonem centralnym (koordynuje go) za pośrednictwem wiązania powstającego w mechanizmie donorowo-akceptorowym. Rolę liganda może odgrywać każda cząsteczka lub jon, dysponujące wolną parą elektronową, przy czym dipole/kwadrupole będą się łączyć z atomem/jonem centralnym poprzez biegun ujemny.
W związku z tym ligandami mogą być pierwiastki tworzące aniony (charakteryzujące się wysoką elektroujemnością) - na przykład aniony tlenu, azotu, siarki, wodoru, fluorowców - oraz cząsteczki zawierające atomy tych pierwiastków, na których zlokalizowana jest co najmniej jedna para elektronowa - na przykład aniony kwasów tlenowych, amoniak i aminy, woda, ketony, etery, fosfiny, arsyny itp. Szczególnie bogaty i ciągle rozszerzający się zbiór ligandów stanowią związki organiczne zawierające atomy tlenu, azotu i fosforu.
Atom/jon centralny w związku (niekoniecznie koordynacyjnym) charakteryzowany jest między innymi przez liczbę koordynacji. Pojęcie to oznacza liczbę atomów, które są bezpośrednio połączone z atomem/jonem centralnym. Definiowanie liczby koordynacji jako liczby ligandów jest błędne, ponieważ istnieje wiele ligandów koordynujących atom/jon centralny przez więcej niż jeden atom, na przykład w jonie kompleksowym [Co(en)3]3+ ligand - etylenodiamina - łączy się z jonem kobaltu przez dwa atomy azotu, więc jon centralny jest otoczony przez 6 atomów (i tyle wynosi jego liczba koordynacji), mimo iż w jednostce koordynacyjnej występują tylko trzy cząsteczki liganda.
Ligandy można klasyfikować z punktu widzenia różnych kryteriów. Do prostszych klasyfikacji należą:
Znacznie bardziej użyteczne są jednak klasyfikacje uwzględniające ważniejsze aspekty budowy liganda, naturę wiązania, jakie tworzy ligand z pierwiastkiem centralnym oraz oddziaływanie liganda na atom/jon centralny.
Do ligandów bidentnych należą też wszystkie aniony kwasowe (organiczne i nieorganiczne), choć najczęściej nie są one w stanie koordynować danego atomu/jonu centralnego przez więcej niż jeden atom tlenu - mogą jednak stanowić mostki w kompleksach wielordzeniowych (jak anion CH3CO2- w dihydracie tetraoctanu dimiedzi(II)). Może się zatem zdarzyć, że dany ligand będzie mieć więcej atomów donorowych, niż jest w stanie obsadzić miejsc koordynacji - na przykład jon BF4-, z uwagi na swoją budowę tetraedryczną, może koordynować atom/jon centralny najwyżej przez trzy atomy fluoru, a i to tylko w wyjątkowych przypadkach.
Trzeba jeszcze raz podkreślić, że wszystkie grupy ligandów z tej klasyfikacji, także π-donory i π-akceptory, tworzą wiązanie σ z atomem/jonem centralnym. Ponadto nie należy jej mylić z klasyfikacją z punktu 5, w której występują podobne nazwy. W dalszej części skryptu pojęcia „ligandy σ-donorowe”, „ligandy π-donorowe” i „ligandy π-akceptorowe” dotyczą klasyfikacji z punktu 6.
Ligandy uporządkowane według siły pola tworzą tzw. szereg spektrochemiczny ligandów. Niezależnie od tego, można je podzielić na trzy grupy:
Wielkość rozszczepienia decyduje o tym, czy orbitale molekularne kompleksu, mające charakter orbitali walencyjnych atomu/jonu centralnego, są zapełniane zgodnie z regułą Hunda, czy też nie. W konsekwencji siła pola ligandów decyduje o właściwościach magnetycznych związków kompleksowych. Ligandy silnego pola powodują większe sparowanie elektronów walencyjnych atomu/jonu centralnego niż ligandy słabego pola, dlatego kompleksy z ligandami silnego pola są zwykle niskospinowe, a kompleksy z ligandami słabego pola - wysokospinowe.
Należy tutaj podkreślić, że określenia „wysoko-” i „niskospinowe” dotyczą wyłącznie kompleksów. Nazywanie ligandów silnego pola „niskospinowymi”, a ligandów słabego pola „wysokospinowymi” jest absolutnie niedopuszczalne! Terminy te dotyczą konfiguracji elektronowej atomu/jonu centralnego w kompleksie, podczas gdy stan spinowy każdego liganda jest w danych warunkach stały i niezależny od atomu/jonu centralnego, z którym ligand tworzy kompleks.
Należy też unikać stosowania określeń „ligandy parujące elektrony” i „ligandy nie parujące elektronów” jako synonimów ligandów silnego i ligandów słabego pola. To, czy dany ligand powoduje sparowanie elektronów atomu/jonu centralnego w kompleksie, zależy bowiem nie tylko od rodzaju liganda, ale także od rodzaju atomu/jonu centralnego (patrz przypis 21). Ten sam ligand może tworzyć kompleks niskospinowy z jednym jonem centralnym, a wysokospinowy - z innym (niekiedy nawet są to jony tego samego pierwiastka!). Jest to widoczne zwłaszcza w przypadku ligandów σ-donorowych.
Ligandy obojętne mają nazwy stosowane w mianowniku i poza nielicznymi wyjątkami (na przykład amoniak jako ligand nosi nazwę „amina”) takie same, jak nazwa związku. Jeśli ligandem jest cząsteczka pierwiastka, nosi on nazwę zgodną z zasadami tworzenia nazw cząsteczek homopoliatomowych.
Nazwy ligandów anionowych tworzy się przez dodanie do nazwy jonu przyrostka „o” (na przykład jon NO3- występujący jako ligand nosi nazwę „azotano(V)”). Do wyjątków należą proste aniony, na przykład halogenkowe: jon chlorkowy jako ligand nosi nazwę „chloro”. W przypadku, gdy ligandem jest anion kwasowy, najpewniejszą metodą jest zastosowanie nomenklatury wodorowej z podaniem stopnia utlenienia pierwiastka tworzącego anion.
Nazwy ligandów stanowiących obojętne związki organiczne stosuje się bez zmian. Niekiedy używa się tu starszych nazw związków organicznych, zalecane jest jednak stosowanie nazw systematycznych zalecanych przez IUPAC.
Tabela 11. obejmuje najważniejsze ligandy nieorganiczne i organiczne, w żadnym wypadku nie stanowi jednak pełnego wykazu ligandów. W razie wątpliwości co do nazwy danego liganda organicznego należy posiłkować się zasadami nomenklatury związków organicznych.
Przegląd ligandów wraz z ich nazwami.
Wzór sumaryczny lub półstrukturalny |
Nazwa liganda w kompleksie |
Skrót stosowany we wzorach i inne ewentualne uwagi |
|
H2 |
diwodór |
|
|
H- |
hydrydo |
Wyjątkowo w przypadku wodorkowych kompleksów boru, takich jak [BH4]-, dopuszczalna jest nazwa „hydro”. |
|
D- |
[2H]hydrydo |
|
|
C22- |
acetyleno |
|
|
CO |
karbonyl |
|
|
CS |
tiokarbonyl |
|
|
CO32- |
węglano |
|
|
H2C=CH2 |
etylen (eten) |
|
|
C6H6 |
benzen |
|
|
C8H12 |
cyklooktadien |
cod |
|
C5H5- |
cyklopentadieno |
Cp lub cp; grupa kompleksów z dwoma anionami C5H5- lub ich pochodnymi nazywa się metalocenami. |
|
CH3O- |
metanolano |
W analogiczny sposób nazywa się aniony pozostałych alkoholanów. |
|
HCO2- |
metaniano, mrówczano |
W analogiczny sposób nazywa się aniony pochodzące od pozostałych kwasów karboksylowych. |
|
CH3CO2- |
etaniano, octano |
|
|
(CO2)22- |
etanodiano, szczawiano |
ox |
|
[CH3CO(CH)COCH3]- |
acetyloacetono, |
acac (acetyloaceton w postaci cząsteczki obojętnej oznaczany jest skrótem Hacac) |
|
N2 |
diazot |
|
|
N22- |
dinitrydo(2-) |
|
|
N24- |
dinitrydo(4-) |
|
|
N3- |
nitrydo |
|
|
N3- |
azydo, trinitrydo |
|
|
NO2- |
azotano(III) |
|
|
NO3- |
azotano(V) |
|
|
(N2O2)2- |
dioksodiazotano(I) |
|
|
NH3 |
amina, azan |
|
|
NF3 |
trifluoroazan |
|
|
NH2- |
amido |
|
|
NH2- |
imido |
|
|
(CH3)2N- |
dimetyloamido |
|
|
CH3CONH- |
acetamido |
|
|
N2H4 |
hydrazyna, diazan |
|
|
N2H2 |
diimina, diazen |
|
|
H2NNH- |
hydrazydo |
|
|
NNH22- |
hydrazydo(2-)-N,N |
|
|
HNNH2- |
hydrazydo(2-)-N,N' |
|
|
CH3NH2 |
metyloamina |
W analogiczny sposób nazywa się pozostałe aminy organiczne występujące jako ligandy. |
|
(CH3)2NH |
dimetyloamina |
|
|
(CH3)3N |
trimetyloamina |
|
|
H2NCH2CH2NH2 |
etylenodiamina |
en |
|
H2NCH2CH2(NH)CH2CH2NH2 |
dietylenotriamina |
dien, w analogiczny sposób powstają nazwy zwyczajowe pozostałych poliamin tego szeregu. |
|
|
azolidyna (pirolidyna) |
|
|
|
azol (pirol) |
|
|
|
azyna (pirydyna) |
py |
|
|
1,4-diazyna (pirazyna) |
|
|
|
chinolina |
|
|
|
8-hydroksychinolina |
oxinate; jako ligand występuje w postaci anionu |
|
|
bipiridyl |
bipy, bpy |
|
|
1,10-fenantrolina |
phen |
|
NH2OH |
hydroksyloamina (hydroksoazan) |
|
|
H2NCH2CH2OH |
etanoloamina, 2-aminoetanol |
Hea |
|
NO |
nitrozyl, tlenek azotu(II) |
|
|
NS |
tionitrozyl, siarczek azotu(II) |
|
|
N2O |
azotek tlenek azotu(V) |
|
|
EDTA |
kwas etylenodiaminotetraoctowy, kwas (etano-1,2-diylodinitrylo)tetraoctowy |
H4edta; w kompleksach występuje też w formie w różnym stopniu zdeprotonowanej |
|
(NH2)2CO |
mocznik |
ur |
|
(NH2)2CS |
tiomocznik |
tu |
|
HCON(CH3)2 |
N,N-dimetyloformamid |
dmf |
|
PH3 |
fosfina |
|
|
PH2(C6H5) |
(mono)fenylofosfina |
mpp |
|
PH(C6H5)2 |
difenylofosfina |
dpp |
|
P(C6H5)3 |
trifenylofosfina |
PPh3, tpp |
|
P(CH3)2(C6H5) |
fenylodimetylofosfina |
PMe2Ph, dmpp |
|
(C6H5)2PCH2CH2P(C6H5)2 |
bis-(1,2-difenylofosfino)etan, difos, etano-1,2-diylobis(difenylofosfina) |
dppe |
|
PO43- |
ortofosforano(V) |
|
|
P2O74- |
μ-okso-heksadioksodifosforano(4-), disfosforano(V) |
|
|
As(C6H5)3 |
trifenyloarsyna |
AsPh3, triars, tpa |
|
AsO33- |
arseniano(III) |
|
|
AsO43- |
arseniano(V) |
|
|
O2 |
ditlen |
|
|
O2- |
okso (oksydo) |
|
|
O22- |
perokso, dioksydo(2-) |
|
|
O2- |
superokso, dioksydo(1-) |
|
|
O3- |
ozonido, trioksydo(1-) |
|
|
H2O |
akwa |
|
|
OH- |
hydrokso |
|
|
H2O2 |
nadtlenek wodoru |
|
|
HO2- |
hydroperokso |
|
|
|
oksol (furan) |
|
|
|
oksolan (tetrahydrofuran) |
thf |
|
|
oksan (tetrahydropiran) |
|
|
|
1,4-dioksan (dioksan) |
|
|
H2S |
sulfan |
|
|
HS- |
sulfanido, hydrosulfido |
|
|
S2- |
tio, sulfido |
|
|
H2S2 |
disulfan |
|
|
HS2- |
disulfanido, hydrodisulfido |
|
|
S22- |
ditio, disulfido(2-) |
|
|
H2S5 |
pentasulfan |
|
|
SO42- |
siarczano(VI) |
|
|
S2O32- |
tiosiarczano(VI), trioksotiosiarczano(2-) |
|
|
S2O62- |
heksaoksodisiarczano(S-S)(2-), ditioniano(V) |
|
|
S2O72- |
μ-okso-heksaoksodisiarczano(2-), disiarczano(VI) |
|
|
maximum record size = 517
record size = 3424780288
|
tiol (tiofen) |
|
|
|
tiolan (tetrahydrotiofen) |
|
|
(CH3)2SO |
dimetylosulfotlenek, sulfinylodimetan |
dmso |
|
H2Se |
selan |
|
|
HSe- |
selanido, hydroselenido |
|
|
Se2- |
selenido |
|
|
H2Se2 |
diselan |
|
|
Se22- |
diselenido(2-) |
|
|
SeO22- |
seleniano(II), dioksoseleniano(2-) |
|
|
H2Te |
tellan |
|
|
HTe- |
tellanido, hydrotellurydo |
|
|
Te2- |
tellurydo |
|
|
Te22- |
ditellurydo(2-) |
|
|
TeO66- |
heksaoksotellurano(6-) |
|
|
F2 |
difluor |
W analogiczny sposób tworzy się nazwy pozostałych halogenów i jonów halogenkowych występujących jako ligandów. |
|
F- |
fluoro |
|
|
I3- |
trijodo(1-) |
|
|
[ClF2]- |
difluorochlorano(I) |
|
|
[IF4]- |
tetrafluorojodano(III) |
|
|
[IF6]- |
heksafluorojodano(V) |
|
|
ClO- |
chlorano(I), oksochlorano(1-) |
|
|
[ClO2]- |
chlorano(III), |
|
|
[ClO3]- |
chlorano(V), |
|
|
[ClO4]- |
chlorano(VII), |
|
|
[IO6]- |
heksaoksojodano(VII) |
|
|
Przykładowe ligandy makrocykliczne.
Skrót |
Nazwa zwyczajowa |
Nazwa systematyczna |
18-crown-6 |
|
1,4,7,10,13,16-heksaoksacyklooktadekan |
benzo-15-crown-5 |
2,3-benzo-1,4,7,10,13-pentaoksacyklopentadec-2-en |
2,3,5,6,8,9,11,12-oktahydro-1,4,7,10,13-benzopentaoksacyklopentadecen |
[12]aneS4 |
|
1,4,7,10-tetratiacyklododekan |
[14]aneN4, cyklam |
|
1,4,8,11-tetraazacyklotetradekan |
[18]aneP4O2 |
|
1,10-dioksa-4,7,13,16-tetrafosfacyklooktadekan |
H2oep |
oktaetyloporfiryna |
2,3,7,8,12,13,17,18- oktaetyloporfiryna |
ppIX |
protoporfiryna IX |
kwas 3,7,12,17-tetrametylo-8,13-diwinyloporfiryno-2,18-dipropionowy |
Związki koronowe, takie jak etery, tioetery oraz pochodne azotowe i fosforowe charakteryzują się polidentnymi, elastycznymi cząsteczkami, obsadzającymi wiele miejsc koordynacji. Układy porfirynowe z kolei są najczęściej tetradentne. Ich cząsteczki zawierają płaskie pierścienie złożone z czterech jednostek pirolowych (chociaż obecność podstawników pierścieni może sprawiać, że cała cząsteczka jest przestrzenna). Porfiryny mają ogromne znaczenie biologiczne, występują między innymi w hemie (barwniku hemoglobiny, w postaci kompleksu z żelazem(II)) i w chlorofilu (kompleks z magnezem).
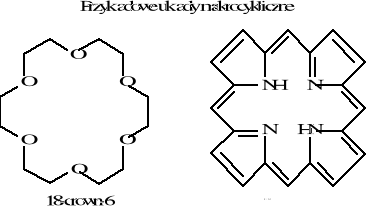
Podstawowy układ porfirynowy jest oznaczany literą p, do której w razie potrzeby dopisuje się litery oznaczające podstawniki lub pochodne zawierające układ porfirynowy, jak w przypadku ftalocyjaniny (oznaczanej pc):
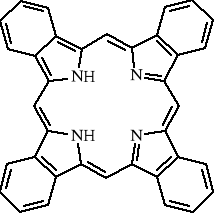
Istnieje wiele rodzajów klasyfikacji związków kompleksowych. Poniżej przedstawiono najważniejsze z nich.
Najważniejsze klasyfikacje związków kompleksowych.
Kryterium |
Klasyfikacja |
Ładunek elektryczny jednostki koordynacyjnej. |
Kompleksy obojętne są pozbawione zewnętrznej sfery koordynacji i tworzą kryształy molekularne. W kompleksach kationowych i anionowych ładunek jonu kompleksowego jest kompensowany obecnością odpowiednich innych jonów, niekiedy także kompleksowych. Związki te tworzą kryształy jonowe. |
Obecność ligandów polidentnych. |
Kompleksy chelatowe - są to kompleksy, w których występują ligandy co najmniej bidentne. Ligand koordynuje ten sam atom/jon centralny co najmniej dwoma atomami donorowymi. Przykłady: [Fe(ox)3]3-, [Co(en)2]3+. |
|
Chelaty wewnętrzne - jest to szczególny przypadek kompleksów obojętnych, tworzony przez pierwiastki na dodatnich stopniach utlenienia z ligandami anionowymi, w sytuacji, gdy ładunki ligandów neutralizują ładunek jonu centralnego. Przykłady: [W(ox)6], kompleks glinu z 8-hydroksychinoliną, kompleks cyrkonu(IV) z EDTA, [Fe(C5H5)2]. |
Liczba atomów/jonów „centralnych” w jednostce koordynacyjnej. |
|
Obecność wiązań między atomami/jonami „centralnymi”. |
Kompleksy klasterowe - jest to szczególny przypadek kompleksów wielordzeniowych, w których oprócz lub zamiast ligandów pełniących rolę mostków między atomami/jonami „centralnymi” występuje wiązanie między tymi atomami lub jonami. Przykłady: [Cr(CO)2(η-C6H6)]2, [Nb3I8]3+, [Mo6Cl8]4+, [Re3Br9], [Mo2Cl8]2-. |
Wypadkowy spin elektronów walencyjnych atomu/jonu centralnego. |
|
Właściwości magnetyczne. |
Istnieją też pewne związki kompleksowe, w których oddziaływanie między elektronami dwóch jonów metali jest nietypowe. Na przykład karboksylanowe kompleksy miedzi(II), takie jak [Cu2(CH3CO2)4(H2O)2], mają charakter antyferromagnetyków. Oddziaływanie między jonami miedzi nie prowadzi w tym kompleksie do powstania zwykłego wiązania metal-metal, ponieważ odległość między nimi jest zbyt duża. |
Główna liczba kwantowa orbitali d wykorzystanych do tworzenia wiązań między atomem/jonem centralnym a ligandami. |
Kompleks nie może być równocześnie wewnątrz- i zewnątrzorbitalowy. |
Obecność wolnych orbitali d na poziomie orbitalowym wykorzystanym do tworzenia wiązań między atomem/jonem centralnym a ligandami. |
Podstawową regułą tworzenia nazw związków kompleksowych jest zasada addytywności. Zgodnie z tą zasadą: nazwę związku tworzy się, łącząc nazwy ligandów (poprzedzone w razie potrzeby odpowiednimi przedrostkami liczbowymi) z nazwą atomu/jonu centralnego (również poprzedzoną w razie potrzeby odpowiednim przedrostkiem liczbowym). Niezbędne jest podanie ładunku jednostki koordynacyjnej lub stopnia utlenienia atomu/jonu centralnego; przy czym system Stocka wydaje się pewniejszy.
We wzorze związku kompleksowego kationowe jednostki koordynacyjne mają pierwszeństwo przed anionowymi. Pisząc wzór jednostki koordynacyjnej, atom/jon centralny wymienia się zawsze jako pierwszy. Następnie podaje się ligandy anionowe w kolejności alfabetycznej według pierwszych symboli ich wzorów, a potem ligandy obojętne ułożone według tej samej zasady. Ligandy polidentne zapisuje się we wzorze w tej samej kolejności alfabetycznej, co monodentne.
Należy pamiętać, że budowa związku kompleksowego wymusza niekiedy odstępowanie od tej zasady. Niektórzy autorzy stosują zasadę wymieniania na początku wzoru liganda tego atomu, przez który ligand koordynuje atom/jon centralny: bez zmian dla amoniaku NH3, ale OH2 dla wody. Jest to szczególnie istotne w przypadku ligandów ambidentnych. Poza tym ligandy o skomplikowanej budowie często oznacza się we wzorach skrótami.
Wzór związku kompleksowego zapisujemy bez odstępów. Wszystkie odrębne jednostki koordynacyjne, występujące we wzorze, zapisujemy w osobnych nawiasach kwadratowych - nawias kwadratowy we wzorze jest zwykle zastrzeżony dla oznaczenia granic jednostki koordynacyjnej! Ligandy złożone zapisujemy w nawiasie okrągłym, nawet jeśli w danej jednostce koordynacyjnej występuje tylko jeden taki ligand:
[CoCl(NO2)(NH3)4]Cl
Dzięki temu wiadomo, że atomy zapisane bez nawiasów stanowią zawsze odrębne ligandy proste. W przypadku nawiasów zagnieżdżających się w następnej kolejności najlepiej używać nawiasu klamrowego:
[CuCl2{O=C(NH2)2}2]
Przy tworzeniu nazwy związku kompleksowego najpierw wymienia się wszystkie ligandy w kolejności alfabetycznej nazw (z ewentualnymi przedrostkami liczbowymi, które nie wpływają na kolejność). Na koniec podaje się nazwy atomów/jonów centralnych w kolejności alfabetycznej (jw.). Jeśli dany atom/jon centralny tworzy związki na więcej niż jednym stopniu utlenienia, podajemy jego stopień utlenienia w danym związku kompleksowym (lub ładunek jednostki koordynacyjnej); w wyjątkowych przypadkach, gdy ustalenie stopnia utlenienia nie jest możliwe, system Ewansa-Bassetta stanowi jedyną możliwość. Nazwę jednostki koordynacyjnej zapisuje się bez odstępów - w postaci jednego słowa!
Szczególną staranność należy zachować przy tworzeniu nazw jednostek koordynacyjnych zawierających ligandy, których nazwy obejmują już przedrostki liczbowe, takich jak diazot, trifenylofosfina itp. Przedrostki liczbowe stanowiące integralną część nazwy liganda mają wpływ na kolejność wymieniania. Jeśli jednostka koordynacyjna zawiera kilka cząsteczek takiego liganda, do określenia ich liczby stosuje się przedrostki bis-, tris-, tetrakis-, pentakis- itd. zamiast zwykłych bi-, tri-, tetra-, penta- itd.
Dodatkowe symbole używane przy zapisywania wzorów i nazw związków kompleksowych.
Symbol |
Znaczenie |
μ |
Ligand jest mostkowy, to znaczy łączy dwa lub więcej atomów/jonów; liczbę atomów mostkowanych można podać w indeksie dolnym, na przykład μ3 (gdy mostek łączy dwa atomy, indeks ten jest zwykle pomijany). |
η |
Ligand jest koordynowany bocznie, jak na przykład etylen, diazot, benzen lub anion cyklopentadienylowy. Liczba w górnym indeksie odpowiada liczbie atomów wchodzących w kontakt z atomem/jonem centralnym, na przykład η2 (etylen, diazot, diwodór), η5 (anion cyklopentadienylowy). |
κ |
Wskazuje donorowy atom liganda polidentnego w kompleksie chelatowym lub liganda ambidentnego; liczba w górnym indeksie odpowiada liczbie atomów donorowych liganda, biorących udział w tworzeniu wiązań z atomem/jonem centralnym. Na przykład difos, koordynujący za pośrednictwem dwóch atomów fosforu, uzyskuje w nazwie kompleksu oznaczenie κ2P. |
Zagnieżdżone nawiasy w nazwach związków kompleksowych oznacza się kolejno (), [] i {}. Nawiasami obejmuje się zawsze nazwy ligandów poprzedzonych przedrostkiem bis-, tris-, tetrakis-, pentakis- itd.
Nazwę kationowej jednostki koordynacyjnej rozpoczyna się od słowa kation, a nazwę atomu/jonu centralnego na końcu podaje się w dopełniaczu:
[Ni(H2O)6]2+ - kation heksaakwaniklu(II)
[CoCl(NH3)5]2+ - kation pentaaminachlorokobaltu(III)
[Co(en)3]3+ - kation tris(etylenodiamina)kobaltu(III)
[Fe(CNCH3)6]2+ - kation heksakis(izocyjanek metylu)żelaza(II)
[PtCl(NH2CH3)(NH3)2]+ - kation diaminachloro(metyloamina)platyny(II)
W nazwie obojętnej jednostki koordynacyjnej nazwa atomu/jonu centralnego występuje zawsze w mianowniku:
[Ni(CO)4] - tetrakarbonylnikiel(0)
[CoCl3(NH3)3] - triaminatrichlorokobalt(III)
[Ru(HSO3)2(NH3)4] - tetraaminabis(wodorotrioksosiarczano(IV))ruten(II)
[PtCl2(dpp)(tu)] - dichloro(difenylofosfina)(tiomocznik)platyna(II)
[W(N2)6] - heksakis(diazot)wolfram(0)
[MnFO3] - fluorotrioksomangan(VII)
Nazwę anionowej jednostki koordynacyjnej można rozpocząć od słowa anion, a nazwę atomu/jonu centralnego na końcu podać w dopełniaczu. Bardziej zalecaną i bardziej uniwersalną metodą jest jednak niestosowanie słowa anion, a zamiast tego dodanie do tematu nazwy atomu/jonu centralnego końcówki -an lub -ian:
[PtCl6]2- - heksachloroplatynian(IV)
[OsCl5N]2- - pentachloronitrydoosmian(VI)
[Fe(CN)6]4- - heksacyjanożelazian(II)
[Ni(CN)4]4- - tetracyjanoniklan(0)
[Co(CO)4]- - tetrakarbonylkobalt(-I)
Tworząc nazwy związków kompleksowych z uwzględnieniem przeciwjonów, używa się zasad tworzenia nazw soli (2.5.3.1.):
[Ni(H2O)6](NO3)2 - azotan(V) heksaakwaniklu(II)
[Ag(NH3)2]Cl - chlorek diaminasrebra(I)
K3[TaF8] - oktafluorotantalan(V) potasu
Na3[Al(OH)6] - heksahydroksoglinian sodu
Znane są oczywiście również związki, w których zarówno kationy, jak i aniony mają również charakter koordynacyjny:
[Zn(NH3)4][BF4]2 - tetrafluoroboran tetraaminacynku
[Pt(NH3)4][PtCl6] - heksachloroplatynian(IV) tetraaminaplatyny(II)
[Hg2(H2O)2]2[ReH9] - nonahydrydorenian(VII) diakwadirtęci(I)
[MoOCl(dppe)2]3[Fe(CN)6] - heksacyjanożelazian(III) chlorobis[bis-(1,2-difenylofosfino)etan]oksomolibdenu(IV)
W celu uzyskania maksymalnej ścisłości nazwy kompleksu z ligandem polidentnym można wskazywać w niej atomy, przez które ligand koordynuje atom/jon centralny. Na przykład anion ditioszczawianowy może koordynować centrum koordynacji przez atomy siarki lub tlenu, co oznacza się ditioszczawiano-O,O', ditioszczawiano-S,S' lub ditioszczawiano-O,S. W przypadku różnych atomów donorowych wymienia się je w kolejności alfabetycznej.
W przypadku bardziej złożonych ligandów stosuje się tzw. konwencję κ (kappa). Donorowe atomy liganda wskazuje się za pomocą symbolu pierwiastka, pisanego kursywą i poprzedzonego grecką literą κ. Górny indeks po κ oznacza liczbę jednakowych atomów donorowych. Po symbolu atomu donorowego używa się w razie potrzeby symboli ', ”, '” itd. oraz liczb oznaczających na przykład numer atomu węgla w łańcuchu lub pierścieniu.
Do zilustrowania tych zasad dobrze nadają się kompleksy z EDTA, który może obsadzać 2, 3, 4, 5 lub 6 miejsc koordynacji:

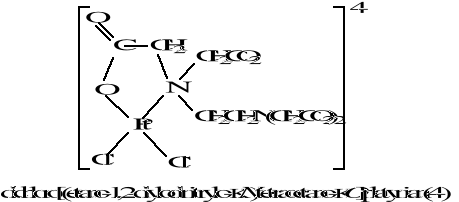
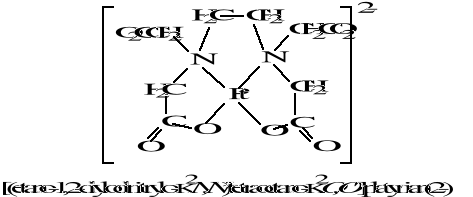
Istnieją trzy rodzaje kompleksowych związków wielordzeniowych:
Ponadto każda z tych klas obejmuje związki symetryczne (zawierające atomy/jony „centralne” jednego pierwiastka) i niesymetryczne (zawierające atomy/jony „centralne” różnych pierwiastków lub centra koordynacji o różnych otoczeniach koordynacyjnych).
Najlepszy opis nomenklaturowy tego typu związków zapewnia tzw. nomenklatura strukturalna. Według jej zasad:
Nazwy przykładowych nieklasterowych kompleksów mostkowych:
[Cr2O7]2- ≡ [(CrO3)2(μ-O)]2- - μ-okso-heksaoksodichromian(VI) lub μ-okso-bis(trioksochromian)(VI)
[Cu2(μ-CH3CO2)4(H2O)2] - diakwa-tetra-μ-octano-dimiedź(II) lub tetra-μ-octano-bis(akwamiedź)(II)
[{Cr(NH3)5}2(μ-OH)]Cl5 - pentachlorek μ-hydrokso-bis(pentaaminachromu)
[{PtCl(PPh3)}2(μ-Cl)2] - di-μ-chloro-bis[chloro(trifenylofosfina)platyna](II)
[{Mo(N2)(dppe)2}2(μ-N2)] - μ-diazot-bis{bis[bis-(1,2-difenylofosfino)etan]diazotmolibden}
Według nomenklatury strukturalnej obecność wiązania między atomami/jonami „centralnymi” zaznacza się w nazwie związku, zapisując w nawiasie okrągłym symbole łączących się atomów, pisane kursywą i połączone długą kreską, na przykład (Cr--Cr), (Mn--Mn). Zapis ten umieszcza się po nazwach atomów centralnych, a przed ładunkiem jednostki koordynacyjnej (stopniem utlenienia atomu/jonu centralnego). Nazwy przykładowych kompleksów klasterowych (bez mostków):
[Mn2(CO)10] ≡ [{Mn(CO)5}2] - dekakarbonyldimangan(Mn--Mn) lub bis(pentakarbonylmangan)(Mn--Mn)(0)
[Cr2(C6H6)2(CO)4] ≡ [{Cr(C6H6)(CO)2}2] - bis(η6-benzen)tetrakarbonyldichrom(Cr--Cr) lub bis(η6-benzendikarbonylchrom)(Cr--Cr)(0)
[Re2Cl8]2- - oktachlorodirenian(Re--Re)(III) lub bis(tetrachlororenian)(Re--Re)(2-)
Nazwy przykładowych klasterów mostkowych:
[Mo2(μ-CH3CO2)4(H2O)2] - diakwa-tetra-μ-octano-dimolibden(Mo--Mo)(II) lub tetra-μ-octano-bis(akwamolibden)(Mo--Mo)(II)
[Co2(CO)8] ≡ [Co2(CO)6(μ-CO)2] - di-μ-karbonyl-heksakarbonyldikobalt(Co--Co)
[W2Cl9]3- ≡ [W2Cl6(μ-Cl)3]3- ≡ [(WCl3)2(μ-Cl)3]3- - tri-μ-chloro-heksachlorodiwolframian(W--W)(3-) lub tri-μ-chloro-bis(trichlorowolframian)(W--W)(III)
Dlatego linie widmowe, odpowiadające przeskokom elektronów z jednego stanu energetycznego do drugiego, ulegają w polu magnetycznym rozszczepieniu na większą ilość linii - więcej stanów energetycznych oznacza więcej możliwości przeskoków. Jest to tzw. efekt Zeemana.
Indeksy te oznaczają orientację przestrzenną, co jest wyjaśnione dokładniej w rozdziale 1.12.
Kształt ten wynika oczywiście z podstawienia odpowiednich wartości liczb kwantowych do równania Schrödingera, podobnie jak w przypadku wszystkich pozostałych orbitali.
Otrzymany niedawno w niewielkiej ilości izotop 5H nie ma jeszcze żadnej nazwy i prawdopodobnie jej nie uzyska z uwagi na niewielkie znaczenie praktyczne.
Wymowa „raterford”
Wymowa „s-iborg” (s twarde)
Wymowa „bor” (niestety stwarza to możliwość pomyłki z borem B)
Wymowa „majtner” (podobnie nazwę einsteinu wymawia się „ajnsztajn”)
Łac./ang „quad”, stąd w symbolu pierwiastka temu liczebnikowi odpowiada litera „q”.
Jest ona krytykowana przez znaczną część społeczności chemicznej jako zbyt sztywna i formalna, ale zarzucenie jej jest mało prawdopodobne.
Odkrycie tego pierwiastka jest na razie uważane za niepotwierdzone.
Wg skali Allreda-Rachowa.
Cząsteczka tego związku ma budowę podobną, jak cząsteczka H2O2, dlatego nie można zapisać jego wzoru jako OF.
Zasady nazewnictwa związków kompleksowych i ich pochodnych zostaną przedstawione w dalszej części niniejszego rozdzialu.
Ściślej - koordynujące zawsze tylko przez jeden atom donorowy.
W przypadku ligandów prostych chodzi po prostu o elektrony walencyjne na orbitalach atomowych, które w cząsteczce kompleksu mają symetrię π.
Z wyjątkiem jonu fluorkowego; fluor tworzy wiązania π tylko w nielicznych przypadkach (np. w BF3), ponieważ ma mały promień atomowy i jonowy.
Degeneracja poziomów energetycznych oznacza, że dany poziom składa się z więcej niż jednego orbitalu. I tak w izolowanym atomie poziom orbitalowy p jest zdegenerowany trzykrotnie (składa się z trzech orbitali, px, py i pz, o jednakowej energii), poziom orbitalowy d - pięciokrotnie, a poziom f - siedmiokrotnie.
σ-donory powodujące najsilniejsze rozszczepienie należą do ligandów silnego pola, a σ-donory powodujące najsłabsze rozszczepienie - do ligandów słabego pola. Ponadto trzeba pamiętać, że siła pola ligandów nie jest jedynym parametrem decydującym o rozszczepieniu orbitali atomu/jonu centralnego w kompleksie. Należy uwzględnić też podatność pierwiastka centralnego na oddziaływanie ligandów; jony uporządkowane według tej podatności tworzą szereg spektrochemiczny jonów centralnych.
Widać to szczególnie w przypadku jonów fosforanowych i arsenianowych, gdzie podanie ładunku jonu nie zapewnia informacji niezbędnych do ustalenia wzoru.
Tego typu nazwy ligandów typu anionów kwasowych stosuje się tylko wtedy, gdy cały anion wchodzi w skład wewnętrznej sfery koordynacji atomu/jonu centralnego - zazwyczaj gdy koordynuje go przez więcej niż jeden atom tlenu.
Z wyjątkiem oznaczeń izotopów, takich jak [15N], [2H], oraz jonów o zdelokalizowanym ładunku, nie będących związkami kompleksowymi.
Chyba że sama nazwa liganda składa się z dwóch słów, na przykład „tlenek azotu(II)”.
Podawanie ładunku anionu kompleksowego nie jest w tym przypadku konieczne, ponieważ definiuje go podana wcześniej liczba przeciwjonów (pentachlorek).
2
4
88
Wyszukiwarka
Podobne podstrony:
wstęp, chemia nieorganiczna, zalaczniki2
CHEMIA NIEORGANICZNA 2
Chemia nieorganiczna zadania 4 Nieznany
Chemia nieorganiczna zadania 7 Nieznany
KationyV, Farmacja, I rok, Chemia nieorganiczna
egz 2010-pytania spisane(1), Chemia nieorganiczna- egzmain
Tlenowce(1), Chemia, Chemia nieorganiczna
testy chemia2, Biotechnologia PŁ, chemia nieorganiczna
CHEMIA KOSMETYCZNA Chemia nieorganiczna (tlenki, kwasy, sole
Chemia nieorganiczna egzamin
Chemia nieorganiczna sciaga
iloczynrozw, ~ NOTATKI, przedmioty obowiązkowe I rok, Chemia Nieorganiczna, Kolokwia
Nierganiczna cw teoria, semestr 1, Chemia, Nieorganiczna teoria
odp test 1, 1 ROK Biologia i geologia, spec.Ochrona przyrody, Chemia nieorganiczna
nieorgany-pytania2, Studia - Chemia kosmetyczna UŁ, II rok, III semestr, CHEMIA NIEORGANICZNA labora
KationyIIB, Farmacja, I rok, Chemia nieorganiczna
ligandy, Studia POLSL, STUDIA, Chemia nieorganiczna, teoria
więcej podobnych podstron