1. Ciągi skończone i nieskończone.

2. Przestrzenie liniowe, metryczne, unormowane i przestrzenie liniowe z iloczynem skalarnym.

3. Układy funkcji ortogonalnych. Układ trygonometryczny

4. Układy funkcji ortogonalnych. Wielomiany Legendre'a
   .

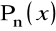
5. Układy funkcji ortogonalnych. Wielomiany Czebyszev'a pierwszego rodzaju
   .

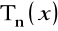
6. Układy funkcji ortogonalnych. Wielomiany Laguerre'a
   .

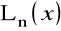
7. Układy funkcji ortogonalnych. Wielomiany Hermite'a
   .

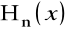
8. Błędy bezwzględne i względne liczby przybliżonej. Źródła błędów.

9. Błędy bezwzględne i względne liczby przybliżonej. Błędy działań arytmetycznych.

10. Błędy bezwzględne i względne liczby przybliżonej. Błąd funkcji jednej zmiennej.

11. Parametry rozkładów wielkości fizycznych. Rodzaje średnich i odchylenie standardowe.

12. Rozkład normalny i jego parametry.

13. Obliczanie niepewności pomiarów pośrednich. Obliczanie odchyleń standartowych.

14. Obliczanie niepewności pomiarów pośrednich. Obliczanie niepewności maksymalnych.

15. Wartości własne i wektory własne macierzy.

16. Układ równań liniowych. Przekształcenia elementarne.

17. Układ równań liniowych. Twierdzenia o istnieniu rozwiązania.

18. Układ równań liniowych. Metody dokładne ich rozwiązania.

19. Układ równań liniowych. Metoda eliminacji Gaussa (schemat blokowy).

20. Układ równań liniowych. Metoda eliminacji Jordana (schemat blokowy).

21. Układ równań liniowych. Metoda kolejnych przybliżeń (schemat blokowy).

22. Układ równań liniowych. Metoda Seidla (schemat blokowy).

23. Rozwiązywanie numeryczne równań nieliniowych. Wyznaczanie przedziałów izolacji (schemat blokowy).

24. Rozwiązywanie numeryczne równań nieliniowych. Metoda równego podziału (schemat blokowy).

25. Rozwiązywanie numeryczne równań nieliniowych. Metoda siecznych (schemat blokowy).

26. Rozwiązywanie numeryczne równań nieliniowych. Metoda stycznych (schemat blokowy).

27. Rozwiązywanie numeryczne równań nieliniowych. Metoda iteracji (schemat blokowy).

28. Zagadnienie interpolacji. Wielomian interpolacyjny Taylor'a.

29. Zagadnienie interpolacji. Różnice progresywne i różnice wsteczne.

30. Zagadnienie interpolacji. Wzory interpolacyjne Newtona.

31. Zagadnienie interpolacji. Wzór interpolacyjny Lagrange'a.

32. Zagadnienie interpolacji. Wzory interpolacyjne Gaussa.

33. Zagadnienie interpolacji. Interpolacja funkcjami sklejanymi.

34. Aproksymacja funkcji. Rodzaje aproksymacji.

35. Aproksymacja interpolacyjna a jednostajna. Podstawowe twierdzenia.

36. Aproksymacja w przestrzeni unormowanej.

37. Aproksymacja średniokwadratowa. Aproksymacja trygonometryczna.

38. Aproksymacja średniokwadratowa. Aproksymacja wielomianami Legendre'a.

39. Różniczkowanie numeryczne za pocą wielomia­nów interpolacyjnych Newtona i Gaussa.

40. Równania pierwszego rzędu. Równanie Riccati'ego.

41. Równania pierwszego rzędu. Zagadnienie i twierdzenie Cauchy'ego.

42. Równania pierwszego rzędu. Metoda kolejnych przybliżeń Picard'a (iteracja).

43. Równania pierwszego rzędu. Całkowanie za pomocą szeregów. Szereg Taylor'a.

44. Równania pierwszego rzędu. Metody Rungego-Kutty.

45. Równania pierwszego rzędu. Ekstrapolacyjna metoda Adamsa.

46. Całkowanie numeryczne (wzór Newtona-Cotesa). Wzór prostokątów.

47. Całkowanie numeryczne (wzór Newtona-Cotesa). Wzór trapezów.

48. Całkowanie numeryczne (wzór Newtona-Cotesa). Wzór Simpsona.

---