Zadanie 1) W wyniku przeprowadzonego badania ustalono, iż współczynniki korelacji Pearsona wynoszą - między stażem pracy a wydajnością 0,93 między stażem pracy a płacą 0,88 między płacą a wydajnością 0,90.

Przeciętny staż pracy jest równy 8 lat, przeciętna wydajność 5 szt./godz. zaś przeciętna płaca 1500 zł.

Odchylenie standardowe płacy wynosi 252 zł a odchylenie standardowe wydajności 2 szt./godz.

Ponadto ustalono, iż wzrost stażu pracy o rok wiąże się ze wzrostem płacy średnio o 45 zł przy stałej wydajności pracy.

Oszacuj płacę robotnika, którego staż pracy wynosi 15 lat a wydajność
20 szt./godz.

Rozwiązanie:

Naszym celem jest wyznaczenie funkcji regresji y^ = a₀ + a₁⋅x₁ + a₂⋅x₂ i oszacowanie zmiennej Y dla podanych wartości zmiennych x₁ i x₂

Oznaczenia:

Y - płaca (zmienna zależna, bo ją musimy oszacować)

X₁ - staż pracy (pierwsza zmienna niezależna)

X₂ - wydajność (druga zmienna niezależna)

Dane:

Współczynniki korelacji całkowitej Pearsona: rx1y = 0,88 rx2y = 0,90 rx1x2 = 0,93

Średnie: = 8 = 5 = 1500

Odchylenia: sx1 = nie jest podane sx2 = 2 sy = 252

Przedostatnie zdanie mówi, że parametr a₁ funkcji regresji wynosi 45.

Obliczenia:

Najpierw wyznaczamy parametr a₂ funkcji regresji ze wzoru:

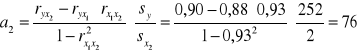
Następnie wyraz wolny a₀ ze wzoru:

Otrzymujemy funkcję regresji y^ = 760 + 45⋅x₁ + 76⋅x₂ , do której podstawiamy x₁=15 oraz x₂=20 co daje wynik 2955 zł.

Do prognozy musimy jeszcze uwzględnić odchylenie standardowe składnika resztowego (średni błąd prognozy) czyli Sy:

gdzie: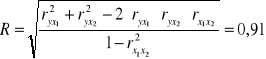

(współczynnik korelacji wielorakiej)

Komentarz:

Przy stażu pracy 15 lat i wydajności 20 sztuk należy się spodziewać płacy wynoszącej teoretycznie 2955 zł, która przeciętnie może się wahać o ± 106 zł

---