Wydział Automatyki Elektroniki i Informatyki

Zjawisko Halla

Informatyka, sem.2, gr.2, sekcja 10

Sebastian Gaś

Kornel Grzywocz

Marek Nowak

1. Wstęp teoretyczny.

W roku 1879 E. H. Hall przeprowadził doświadczenie, które w łatwy sposób pozwala określić znak ładunku płynącego w przewodniku lub półprzewodniku. Zjawisko to, nazwane później zjawiskiem Halla, związane jest z oddziaływaniem stałego pola magnetycznego na ru­chome nośniki ładunku. Jeśli np. przez płaski pasek miedziany, przepuścić prąd o natężeniu I i umieścić go w prostopadłym do jego powierzchni jednorodnym polu magnetycznym o indukcji B, to na każdy elektron swobodny uczestniczący w ruchu uporządkowanym działa siła prosto­padła zarówno do wektora B, jak i do wektora j (gęstości), która nazywana jest siłą Lorenza.

Rys. 1.: Powstawanie napięcia Halla w płytce półprzewodnika.

Siła ta jest określona ­wzorem :

(1) F = qVxB

zaś związek między wektorem gęstości prądu j i prędkością (zwaną prędkością unoszenia elek­tronów) jest następujący:

(2) j = neVu

gdzie

n - gęstość objętościowa ładunku (koncentracja elektronów w

jednostce objętości)

e - ładunek elektronu

Vu - prędkość unoszenia elektronów

(3)

gdzie

I - natężenie prądu

S - przekrój przewodnika

Skutkiem działania tej siły jest odchylenie elektronów ku jednej krawędzi paska i powstanie tam nadmiaru elektronów. Na drugiej krawędzi niedomiar elektronów jest równoważny powstaniu ładunku dodatniego. Tak więc na krawędziach paska zgromadzą się ładunki o przeciwnych znakach. Tę różnicę potencjałów UH nazywamy napięciem Halla. Oczywiście gęstość elektro­nów na jednej krawędzi nie będzie rosnąć nieograniczenie. Proces ów będzie trwał tak długo, dopóki powstałe w jego wyniku poprzeczne pole elektryczne o natężeniu E nie wytworzy siły, która zrównoważy działającą na te nośniki siłę Lorenza.

(4) qEH + q(VuxB )

lub inaczej:

(5) EH = -VuxB

Z równania tego jasno widać, że jeżeli zmierzymy EH i B, to będziemy mogli określić za­równo wartość bezwzględną, jak i kierunek Vu. Znając kierunek prędkości możemy podać znak nośników ładunków.

Jako że:

(6) U = EH b

to uwzględniając (6) zapiszemy:

(7) U = -Vu B b

gdzie

b - szerokość płytki (odległość między punktami A i B).

Uwzględniając wzory (2) i (3) otrzymujemy:

(8) IH = n e Vu b d

gdzie

n - gęstość objętościowa elektronów w przewodniku

e - ładunek elektronu

Vu - prędkość unoszenia elektronów

b - szerokość płytki

d - grubość płytki

Wielkością charakteryzującą zjawisko Halla jest tzw. stała Halla zdefiniowana następująco:

(9)

Ponieważ: , to mając na uwadze zmienną wartość napięcia Halla dla zada­nej wartości indukcji magnetycznej B można bez trudu wyznaczyć stałą Halla R_H, a co za tym idzie koncentrację nośników ładunku w płytce półprzewodnika.

Zjawisko Halla zostało wykorzystane do budowy elementów półprzewodnikowych tzw. hallotronów. Hallotrony stosowane są do pomiarów natężenia pola magnetycznego, pomiaru mocy w technice mikrofalowej, regulacji natężenia pola magnetycznego, pomiaru mocy czynnej i biernej. Najczęściej są one zbudowane z warstwy półprzewodnikowej, antymonku (InSb lub arsenku indu (InAs), naniesionej na płytkę ceramiczną, szklaną lub mikową.

2. Stanowisko pomiarowe.

Źródłem pola magnetycznego jest solenoid o całkowitej liczbie zwojów N = 3000 i długo­ści l = 97.5 cm, w którego uzwojeniu płynie prąd o stałym natężeniu Is, mierzonym za pomocą podłączonego do niego amperomierza (rys. 2). Badana płytka półprzewodnika (hallotron) umieszczona jest wewnątrz solenoidu. Pole magnetyczne wewnątrz solenoidu można uważać za jednorodne. Grubość hallotronu wynosi 2 m.

Schemat obwodu służącego do pomiaru napięcia Halla i natężenia płynącego przez hallo­tron przedstawia rysunek 2.

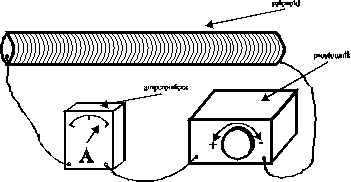
Rys. 2.: Pomiar natężenia prądu w solenoidzie

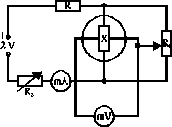
Rys.3.: Schemat obwodu pomiarowego do pomiaru prądu i napięcia Halla: X - hallotron, mA, mV - miliamperomierz i miliwoltomierz

3. Przebieg pomiarów.

Po zapoznaniu się ze schematem pomiarowym przeprowadzono 5 serii pomiarów napię­cia Halla U_H dla zadanych wartości prądu I_H. Każda z serii pomiarowej przeprowadzona była dla innej wartości prądu płynącego przez solenoid Is, a co się z tym wiąże dla innej wartości indukcji magnetycznej B.

Ustalone wartości prądu Is były następujące: 2A, 3A, 4A, 5A, 6A, zaś zadane wartości prądu Ih: 2 mA, 4 mA, 6 mA, 8 mA, 10 mA, 12 mA, 14 mA, 16 mA, 18 mA, 20 mA, 22 mA, 24 mA, 26 mA, 28 mA, 30 mA.

Odpowiednie wartości napięć Halla U_H odczytywane były na jednym zakresie miernika w celu uniknięcia dodatkowych błędów związanych z samym ustrojem pomiarowym.

4. Wyniki pomiarów.

Po dokonaniu pomiarów zyskano następujące wyniki:

IS=2A			IS=3A			IS=4A			IS=5A			IS=6A
IH	UH	IH	UH	IH	UH	IH	UH	IH	UH
[mA]	[mV]	[mA]	[mV]	[mA]	[mV]	[mA]	[mV]	[mA]	[mV]
2	0,1	2	0,3	2	0,5	2	0,6	2	0,9
4	0,3	4	0,7	4	0,9	4	1,2	4	1,5
6	0,5	6	1,0	6	1,4	6	1,9	6	2,3
8	0,8	8	1,4	8	2,0	8	2,6	8	3,2
10	1,2	10	1,8	10	2,5	10	3,4	10	4,1
12	1,5	12	2,2	12	3,1	12	4,1	12	4,9
14	1,7	14	2,6	14	3,6	14	4,8	14	5,8
16	1,9	16	3,0	16	4,2	16	5,5	16	6,6
18	2,1	18	3,3	18	4,7	18	6,1	18	7,4
20	2,3	20	3,7	20	5,3	20	6,9	20	8,2
22	2,5	22	4,1	22	5,8	22	7,5	22	9,0
24	2,7	24	4,4	24	6,3	24	8,1	24	9,7
26	2,9	26	4,9	26	6,8	26	8,7	26	10,4
28	3,1	28	5,1	28	7,2	28	9,3	28	11,1
30	3,2	30	5,3	30	7,6	30	9,8	30	11,7

5. Analiza wyników.

A = 0.1143 ±0.0034 [Ω]

B = -0.042 ±0.062 [mV]

A = 0.1848 ±0.0027 [Ω]

B = -0.0037 ±0.044 [mV]

A = 0.2627 ±0.0027 [Ω]

B = -0.076 ±0.050 [mV]

A = 0.3361 ±0.0039 [Ω]

B = -0.010 ±0.070 [mV]

A = 0.3975 ±0.0046 [Ω]

B = 0.093 ±0.084 [mV]

Is	A	dA	R	dR
[A]	[Ω]	[Ω]	[]	[]
2	0.114	0.004	2.95.10-07	0.11.10-07
3	0.185	0.003	3.19.10-07	0.06.10-07
4	0.263	0.003	3.40.10-07	0.04.10-07
5	0.336	0.004	3.48.10-07	0.05.10-07
6	0.398	0.005	3.43.10-07	0.05.10-07

Wartość średnia (ważona): 3.37.10-07

Błąd średniej: 0.03.10-07

Po zaokrągleniu wyników otrzymujemy:

R_H=(3.37 0.3).10-07 ­­

Mając daną stałą Halla można wyznaczyć wartość koncentracji nośników ładunku w płytce hallotronu korzystając z zależności (9):

n=(1.85 0.02).1025

6. Podsumowanie i wnioski.

Wnioski:

1. Hallotron jest elementem liniowym.

Przyczyny błędów:

1. Klasa dokładności mierników analogowych 0,5.

2. Przypuszczalny błąd pomiaru miliamperomierza przy maksymalnym wy­chyleniu dla zakresu 30 mA (patrz wyniki pomiarów).

3. Wpływ zewnętrznych pól magnetycznych dla małej wartości indukcji magnetycznej w solenoidzie wywołanej prądem Is=2 A.

4. Niestabilne zamocowanie hallotronu w solenoidzie.

5. Niestabilne wskazania miliwoltomierza cyfrowego i związany z tym przy­bliżony pomiar.

---