Część obliczeniowa

1. POZ 1 - płyta

• obciążenia płyty:

	Obciążenia char. [kN / m^2]	Współczynnik obciążeniowy [-]	Obciążenia oblicz. [kN / m^2]
stałe:
lastryko (22,0x0,03)	0,66	1,3	0,858
gładź (21,0x0,02)	0,42	1,3	0,546
płyta żelbetowa (25,0x0,10)	2,50	1,1	2,75
tynk (19,0x0,02)	0,38	1,3	0,494
Σ=	3,96		4,648
zmienne:
użytkowe (q)	8,70	1,2	10,440
Σ=	12,66		15,088

• Obliczenia statyczne:

l_S1 = l₁ - 0,50 * b_w + h_f / 2 = 2,00 - 0,50 * 0,20 + 0,10 / 2 = 1,95 [m]

l_S2 = l₂ - b_w = 2,20 - 0,20 = 2,00

gdzie: l_S1, l_S2 - rozpiętości w świetle

b_w - szerokość przekroju teowego

h_f - grubość płyty

M₁ =
=
= 5,22 kNm

M₂ =
=
= 5,49 kNm

M₂ =
=
= 3,78 kNm

Sprawdzenie momentów przęsłowych:

M_cr > | M_min * w|,

gdzie w =
= 0,839

M_cr = f_ctm * w_c,

gdzie f_ctm = 2,2 MPa (dla B25)

w_c =
=
= 0,001(6) m³

M_cr = 2,2 * 0,001(6) = 0,003(6) MNm

• przęsło przyskrajne

M_min =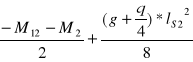
=
= - 1,01 kNm =

= -0,00101 MNm

M_cr > | M_min * w|

0,003(6) > |-0,00101 * 0,839|

0,003(6) > 0,00085

Moment rysujący jest większy niż otrzymany - zbrojenie górą jest zbędne.

• przęsło środkowe

M_min =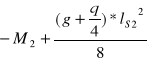
=
= - 0,151 kNm = -0,000151 MNm

M_cr > | M_min * w|

0,003(6) > |-0,000151 * 0,839|

0,003(6) > 0,000127

Moment rysujący jest większy niż otrzymany - zbrojenie górą jest zbędne.

Obliczenie zbrojenia płyty:

• przęsło przyskrajne

A_o =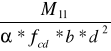
=
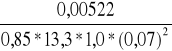
= 0,0939

ξ_eff = 1 -
= 1 -
= 0,0988

ζ_eff = 1 - 0,5 * ξ_eff = 1 - 0,5 * 0,0988 = 0,951

A_S11 =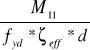
=
= 0,000373 m² = 3,73 cm²

• podpora przyskrajna

A_o =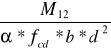
=
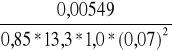
= 0,0991

ξ_eff = 1 -
= 1 -
= 0,1046

ζ_eff = 1 - 0,5 * ξ_eff = 1 - 0,5 * 0,1046 = 0,948

A_S12 =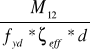
=
= 0,000394 m² = 3,94 cm²

• przęsło środkowe i podpora środkowa

A_o =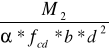
=
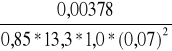
= 0,0682

ξ_eff = 1 -
= 1 -
= 0,0707

ζ_eff = 1 - 0,5 * ξ_eff = 1 - 0,5 * 0,0707 = 0,965

A_S2 =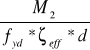
=
= 0,000271 m² = 2,71 cm²

Dobór zbrojenia:

• dla A_S11 = 3,73 cm² → 8φ8 (8 * 0,503 = 4,02 cm²),

• dla A_S2 = 2,71 cm² → dla przęsła - 10φ6 (10 * 0,283 = 2,83 cm²), dla podpory - odginamy z przęsła lewego i prawego po 5φ6 (2 * 5 * 0,283 = 2,83 cm²),

• dla A_S12 = 3,94 cm² → odginamy z przęsła skrajnego 5φ8 i z przęsła przyskrajnego 5φ6 (5 * 0,503 + 5 * 0,283 = 3,93 cm²)

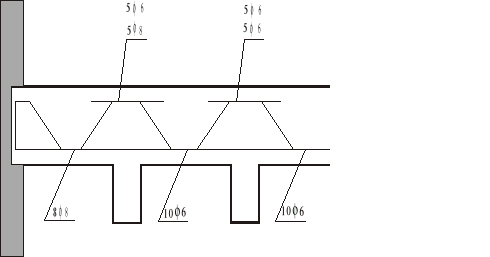
2. POZ 1 - żebro

• obciążenia żebra:

	Obciążenia char. [kN / m^2]	Współczynnik obciążeniowy [-]	Obciążenia oblicz. [kN / m^2]
stałe:
z POZ1 (lastryko+gładź+ tynk) (0,66+0,42+0,38)x2,20	3,21	1,3	4,173
płyta żelbetowa (2,50x2,20)	5,50	1,1	6,050
żebro (0,4-0,1)x0,2x25	1,50	1,1	1,650
Σ=	10,21		11,873
zmienne:
użytkowe (8,70x2,2)	19,14	1,2	22,968
Σ=	29,35		34,841

d =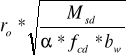

gdzie :

• r_o =
  
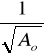
  2,0

• M_sd = 0,8 * M

M =
=
= 136,577 kNm

M_sd = 0,8 * 136,577 = 109,261 kNm

d =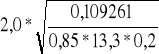
= 0,4397 m

h = d + a = 0,4397 + 0,04 = 0,4797 m

Założona wysokość przekroju okazała się zbyt mała i przyjmuje się nową - h = 0,5 m,

powstaje więc nowa tabela zebrania obciążeń:

	Obciążenia char. [kN / m^2]	Współczynnik obciążeniowy [-]	Obciążenia oblicz. [kN / m^2]
stałe:
z POZ1 (lastryko+gładź+ tynk) (0,66+0,42+0,38)x2,20	3,21	1,3	4,173
płyta żelbetowa (2,50x2,20)	5,50	1,1	6,050
żebro (0,5-0,1)x0,2x25	2,00	1,1	2,20
Σ=	10,71		12,423
zmienne:
użytkowe (8,70x2,2)	19,14	1,2	22,968
Σ=	29,85		35,391

M = (w₁ * g + w_i * q) * l_eff²

V = (w₁ * g + w_i * q) * l_eff

gdzie:

• l_eff = l_n + a₁

natomiast a₁ musi spełniać normowe warunki :

oraz

stąd

oraz

przyjmuje się a₁ = 0,1 m

l_eff = 5,60 + 0,10 = 5,70 m

• w₁, w_i - z tablic Winklera dla belki trójprzęsłowej

M_AB = (0,080 * 12,423 + 0,101 * 22,968) * 5,70² = 107,659 kNm

M_BC = (0,025 * 12,423 + 0,075 * 22,968) * 5,60² = 63,760 kNm

M_B = (-0,100 * 12,423 - 0,117 * 22,968) * 5,70² = -127,671 kNm

V_A = (0,400 * 12,423 + 0,450 * 22,968) * 5,70 = 87,237 kNm

V_B^L = V_C^P = (-0,600 * 12,423 - 0,517 * 22,968) * 5,70 = -110,171 kNm

V_B^P = V_C^L = (0,500 * 12,423 + 0,583 * 22,968) * 5,60= 109,770 kNm

Obliczenie zbrojenia żebra:

Przyjęte wcześniej wymiary:

• h = 0,5 m

• h_f = 0,1 m

• b_w = 0,2 m

• d = h - a = 0,5 - 0,06 = 0,44 m

Przyjmuje się również do zbrojenia żebra stal żebrowaną A III → f_yd = 350 MPa

M_Rd = α * f_cd * b_eff * h_f * (d - 0,5 * h_f) > M_sd - przekrój pozornie teowy

< M_sd - przekrój rzeczywiście teowy

• przęsło przyskrajne (M_sd = 0,108 MNm)

b_eff = bw + lo / 5 = 0,2 + (0,85 * 5,7) / 5 = 1,17 m

b_eff = bw + 2 * b_eff1 = 0,2 + 2 * (6 * 0,1) = 1,40 m

Przyjmuje się wartość b_eff = 1,17 m

M_Rd = 0,85 * 13,3 * 1,17 * 0,1 * (0,44 - 0,5 * 0,1) = 0,516 MNm

0,516 > 0,108

Przekrój jest pozornie teowy - obliczenie zbrojenia jak dla przekroju prostokątnego o b_eff = 1,17 m.

A_o =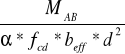
=
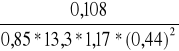
= 0,0422

ξ_eff = 1 -
= 1 -
= 0,0431

ζ_eff = 1 - 0,5 * ξ_eff = 1 - 0,5 * 0,0431 = 0,978

A_S1 =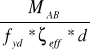
=
= 0,000717 m² = 7,17 cm²

• przęsło środkowe (M_sd = 0,0678 MNm)

b_eff = bw + lo / 5 = 0,2 + (0,70 * 5,60) / 5 = 0,98 m

b_eff = bw + 2 * b_eff1 = 0,2 + 2 * (6 * 0,1) = 1,40 m

Przyjmuje się wartość b_eff = 0,98 m

M_Rd = 0,85 * 13,3 * 0,98 * 0,1 * (0,44 - 0,5 * 0,1) = 0,432 MNm

0,432 > 0,0678

Przekrój jest pozornie teowy - obliczenie zbrojenia jak dla przekroju prostokątnego b_eff = 0,98 m.

A_o =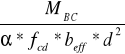
=
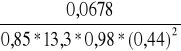
= 0,0316

ξ_eff = 1 -
= 1 -
= 0,0321

ζ_eff = 1 - 0,5 * ξ_eff = 1 - 0,5 * 0,0321 = 0,984

A_S1 =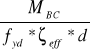
=
= 0,000447 m² = 4,47 cm²

• podpora przyskrajna (M_sd = 0,1277 MNm)

b_w = 0,2 m

M_Rd = 0,85 * 13,3 * 0,2 * 0,1 * (0,44 - 0,5 * 0,1) = 0,088 MNm

0,088 > 0,1277

Przekrój jest pozornie teowy - obliczenie zbrojenia jak dla przekroju prostokątnego o b_w = 0,2 m.

A_o =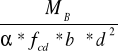
=
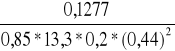
= 0,2917

ξ_eff = 1 -
= 1 -
= 0,3549

ζ_eff = 1 - 0,5 * ξ_eff = 1 - 0,5 * 0,3549 = 0,823

A_S1 =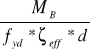
=
= 0,001008 m² = 10,08 cm²

Dobór zbrojenia:

• dla przęsła przyskrajnego A_s = 7,17 cm² → 5φ14 (5 * 1,54 = 7,7 cm²)

• dla przęsła środkowego A_s = 4,47 cm² → 3φ14 (3 * 1,54 = 4,62 cm²)

• dla podpory przyskrajnej A_s = 10,08 cm² → 7φ14 (7 * 1,54 = 10,78 cm²)

Sprawdzenie tabelaryczna rys i ugięcia

Dane: h = 0,5 m

b = 0,2 m

d = 0,44m

• rysy podłużne:

• przęsła skrajne

l_eff = 5,7 m

A_s = 7,7 cm²

wartość charakterystyczna momentu -

M_AB = (0,080 * 10,71 + 0,101 * 19,14) * 5,70² =90,645 kNm

σ_s =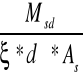

ρ_L =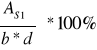
=
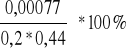
= 0,875 %

dla ρ_L ε (0,5 ; 1,0) ↔ ξ = 0,85

σ_s =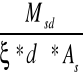
=
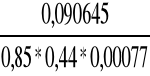
= 314,761 MPa

Dla σ_s = 314,761 MPa oraz ρ_L = 0,875 % odczytano z tablicy D. 1 maksymalną średnicę prętów zbrojenia → φ24 i jest ona większa niż dobrana φ14.

• przęsło środkowe

l_eff = 5,6 m

A_s = 4,62 cm²

wartość charakterystyczna momentu -

M_BC = (0,025 * 10,71 + 0,075 * 19,14) * 5,60² = 53,414 kNm

σ_s =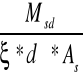

ρ_L =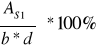
=
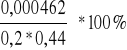
= 0,525 %

dla ρ_L ε (0,5 ; 1,0) ↔ ξ = 0,85

σ_s =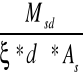
=
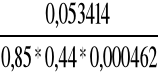
= 309,13 MPa

Dla σ_s = 309,13 MPa oraz ρ_L = 0,525 % odczytano z tablicy D. 1 maksymalną średnicę prętów zbrojenia → φ14 i jest ona równa dobranej φ14.

• rysy ukośne:

Zgodnie z normą PN - B - 03264 pkt 6.4. dla zbrojenia poprzecznego żebra ze stali A-III prętami φ14 wymagane jest sprawdzenie rys ukośnych ze wzoru (99) w/w normy - obliczenia pomijamy.

• ugięcie:

• przęsła skrajne

Dla danych: beton B25, l_eff = 5,7 m < 6,0 m, ρ_L = 0,875 % odczytujemy z tablicy 15 maksymalną wartość stosunku l_eff / d = 23,5

Rzeczywisty stosunek l_eff / d = 5,7 / 0,44 = 12,95

max l_eff / d > l_eff / d

23,5 > 12,95

Ugięcie jest więc dopuszczalne.

• przęsło środkowe

Dla danych: beton B25, l_eff = 5,6 m < 6,0 m, ρ_L = 0,525 % odczytujemy z tablicy 15 maksymalną wartość stosunku l_eff / d = 35

Rzeczywisty stosunek l_eff / d = 5,6 / 0,44 = 12,73

max l_eff / d > l_eff / d

35 > 12,73

Ugięcie jest więc dopuszczalne.

Obliczenie zbrojenia żebra na ścinanie

• podpory skrajne (V_A = V_D) - V_sd = 87,237 kN

V_sd ^k = V_sd - a₁ * (g + q) = 87,237 - 0,1 * (35,391) = 83,698 kN

V_sd ^d = V_sd ^k - d * (g + q) = 83,698 - 0,44 * (35,391) = 68,126 kN

V_Rd1 = [1,4 * k * τ_Rd * (1,2 + 40 * ρ_L) + 0,15 * σ_cp] * b_w* d

k = 1,6 - d = 1,16

τ_Rd dla betonu B25 (z tablicy 13) = 0,26 MPa

ρ_L = 0,00875 < 0,02

σ_cp= 0 (N_sd = 0)

V_Rd1 = [1,4 * 1,16 * 260 * (1,2 + 40 * 0,00875)] * 0,2 * 0,44 = 57,594 kN

V_Rd1 < V_sd ^k - odcinek drugiego rodzaju

V_Rd2 = υ * f_cd * b_w * z *

υ = 0,7 -
= 0,7 -
= 0,6

z = 0,9 * d = 0,9 * 0,44 = 0,396

1 < cotΘ < 2; przyjęto cotΘ = 1,5

V_Rd2 = 0,6 * 13,3 * 0,2 * 0,396 *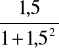
= 291,70 kN

Długość odcinka belki, który podlega ścinaniu:

l_t =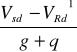
=
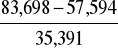
= 0,738 m

Przyjmuje się zbrojenie na odcinku l_t strzemionami φ6 ze stali A-0.

V_Rd3 =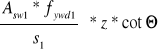
=> s₁ =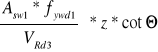

A_sw1 = 2 * π * (0,003)² = 0,57 cm²

f_ywd1 = 190 MPa

s₁ =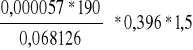
= 0,0944 m = 9,44 cm

Przyjmuje się rozstaw strzemion na odcinku lł co 9 cm.

• podpory przyskrajne (V_B^L = V_C^P) - V_sd = 110,171 kN

V_sd ^k = V_sd - a₁ * (g + q) = 110,171 - 0,1 * (35,391) = 106,632 kN

V_sd ^d = V_sd ^k - d * (g + q) =106,632 - 0,44 * (35,391) = 91,06 kN

V_Rd1 = 57,594 kN < V_sd ^k - odcinek drugiego rodzaju

V_Rd2 = 291,70 kN

l_t =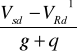
=
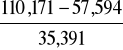
= 1,486 m

Przyjmuje się zbrojenie na odcinku l_t podwójnymi strzemionami φ6 ze stali A-0.

V_Rd3 =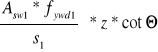
=> s₁ =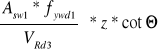

A_sw1 = 4* π * (0,003)² = 1,14 cm²

f_ywd1 = 190 MPa

s₁ =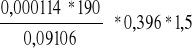
= 0,1413 m = 14,13 cm

0,2 * V_Rd2 = 0,2 * 291,70 = 58,34 kN

0,(6) * V_Rd2 = 0,(6) * 291,70 = 194,467 kN

0,2 * V_Rd2 < V_sd < 0,(6) * V_Rd2

58,34 < 87,237 < 194,467

s_max = 0,6 * d < 30 cm

s_max = 0,6 * 0,44 = 0,264 m

Przyjmuje się rozstaw strzemion na odcinku l_t co 14 cm, natomiast w pozostałej części przęsła AB co 26 cm.

• podpory przyskrajne (V_B^P = V_C^L) - V_sd = 109,977 kN

V_sd ^k = V_sd - a₁ * (g + q) = 109,977 - 0,1 * (35,391) = 106,438 kN

V_sd ^d = V_sd ^k - d * (g + q) =106,438 - 0,44 * (35,391) = 90,866 kN

V_Rd1 = [1,4 * k * τ_Rd * (1,2 + 40 * ρ_L) + 0,15 * σ_cp] * b_w* d

k = 1,16

τ_Rd = 0,26 MPa

ρ_L = 0,00525 < 0,02

σ_cp= 0 (N_sd = 0)

V_Rd1 = [1,4 * 1,16 * 260 * (1,2 + 40 * 0,00525)] * 0,2* 0,44 = 52,391 kN

V_Rd1 < V_sd ^k - odcinek drugiego rodzaju

V_Rd2 = 291,70 kN

Długość odcinka belki, który podlega ścinaniu:

l_t =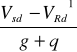
=
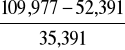
= 1,627 m

Przyjmuje się zbrojenie na odcinku l_t podwójnymi strzemionami φ6 ze stali A-0.

V_Rd3 =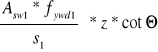
=> s₁ =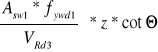

A_sw1 = 4 * π * (0,003)² = 1,14 cm²

f_ywd1 = 190 MPa

s₁ =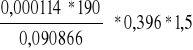
= 0,1416 m = 14,16 cm

Przyjmuje się rozstaw strzemion na odcinku l_t co 14 cm.

---