Wykład 1: Podstawowe pojęcia rachunku prawdopodobieństwa.
Teoria prawdopodobieństwa (także rachunek prawdopodobieństwa lub probabilistyka) to dział matematyki zajmujący się zdarzeniami losowymi.
W teorii prawdopodobieństwa zdarzeniem losowym nazywa się każdy element przestrzeni probabilistycznej (lub przestrzeni zdarzeń). Intuicyjnie, zdarzenie losowe to pewien zbiór możliwych wyników danego eksperymentu. Może być to zarówno pojedynczy wynik, jak i zbiór złożony z większej ilości elementów.
Eksperyment losowy polega np. na rzucie sześcienną kostką do gry. Za zbiór Ω przyjmijmy zbiór możliwych wyników, tzn. Ω = {1,2,3,4,5,6}.
Przykład 1:
- zbiór zdarzeń losowych zdegenerowany. Można je skonstruować dla dowolnego zbioru zdarzeń elementarnych. W tej przestrzeni dysponujemy zatem tylko zdarzeniem niemożliwym
oraz zdarzeniem pewnym Ω.
Zdarzenie losowe niemożliwe - w rachunku prawdopodobieństwa pusty podzbiór przestrzeni zdarzeń elementarnych. Jest ono interpretowane jako zdarzenie losowe, które nie może zaistnieć.
Istnieje tylko jedno zdarzenie niemożliwe (bo jeden jest podzbiór pusty przestrzeni zdarzeń elementarnych), jednak można je uzyskać na różne sposoby. W szczególności zdarzeniem niemożliwym jest iloczyn dowolnych dwóch zdarzeń rozłącznych, np. jednoczesne wyrzucenie jednego oczka i liczby parzystej przy jednokrotnym rzucie kostką do gry.
Zdarzenie losowe pewne - zbiór składający się ze wszystkich zdarzeń elementarnych danej przestrzeni zdarzeń elementarnych. Jest ono interpretowane jako zdarzenie, które musi na pewno zajść.
W danej przestrzeni probabilistycznej istnieje tylko jedno zdarzenie losowe pewne, można je jednak otrzymać na różne sposoby. Przykładem konstrukcji zdarzenia pewnego jest wylosowanie przy dwóch próbach (bez zwracania) przynajmniej jednej czerwonej kuli, podczas gdy w urnie znajduje się tylko jedna kula niebieska i kilka czerwonych.
P(Ω)=1
Przykład 2:
- tutaj zdarzeniami losowymi oprócz niemożliwego i pewnego będą także zbiory {1} oraz {2,3,4,5,6}.
Działania na zdarzeniach losowych:
Suma (alternatywa) zdarzeń

;Iloczyn (koniunkcja) zdarzeń

Zdarzenia rozłączne (wyłączające się): ![]()
∅
Negacja (zdarzenie przeciwne):
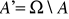
.
Matematyczna teoria prawdopodobieństwa sięga swoimi korzeniami do analizy gier losowych podjętej w siedemnastym wieku przez Pierre de Fermata oraz Blaise Pascala. Z tego powodu, początkowo teoria prawdopodobieństwa zajmowała się niemal wyłącznie zjawiskami dyskretnymi i używała metod kombinatorycznych.
Uwaga !!! : Powtórzyć wiadomości z matematyki dyskretnej z I roku.
Gra losowa - gra, której wynik jest mocno uzależniony od czynników losowych. Do gier tych zwykle używa się kości, urn z kulami, monet, kart czy ruletki.
Pierre de Fermat |
|
Urodzony |
17 sierpnia 1601 |
Zmarł |
12 stycznia 1665 |
|
|
Pierre de Fermat (ur. 17 sierpnia 1601 w Beaumont-de-Lomagne, zm. 12 stycznia 1665 w Castres) - matematyk (samouk) francuski, z wykształcenia prawnik i lingwista, od 1631 radca parlamentu (ówczesna nazwa sądu) w Tuluzie. Większość jego prac opublikował dopiero po jego śmierci syn (1679). Dokonał wielu odkryć w teorii liczb, m.in. sformułował słynne wielkie twierdzenie Fermata i jeszcze przed Kartezjuszem opracował i stosował metodę współrzędnych w geometrii. Wykazał, że wszystkie krzywe drugiego stopnia da się uzyskać przez odpowiednie przecinanie płaszczyzną powierzchni stożka; podał metodę znajdowania ekstremum funkcji. Jego prace stworzyły też podstawy pod późniejszy rozwój rachunku prawdopodobieństwa.
Zobacz też:
Blaise Pascal (1623-1662)
Blaise Pascal (ur. 19 czerwca 1623 w Clermont-Ferrand, zm. 19 sierpnia 1662 w Paryżu) - francuski filozof, matematyk, pisarz i fizyk. Tematem jego badań były prawdopodobieństwo, próżnia, ciśnienie atmosferyczne, oraz apologetyka, teodycea i fideizm. Na jego cześć nazwano jednostkę ciśnienia paskal oraz język programowania Pascal.
Ciekawostki
Blaise Pascal jest wynalazcą ruletki.
Zmienne losowe ciągłe zostały wprowadzone do teorii prawdopodobieństwa znacznie później. Za początek stworzenia współczesnej teorii prawdopodobieństwa powszechnie uważa się jej aksjomatyzację, której w 1933 dokonał Andriej Kołmogorow.
Prawdopodobieństwo a częstość
Przypuśćmy, że ktoś zaproponował nam grę losową: "orzeł wygrywamy, reszka przegrywamy". Na pewno zanim zagramy, będziemy chcieli zbadać jakie są szanse wygranej, przeprowadzamy więc doświadczenie, polegające na wielokrotnym rzucie monetą. Rzucamy 100 razy, orzeł wypadł 48 razy, a więc w 48/100 = 0,48 wszystkich przypadków. Kontynuujemy doświadczenie, po 1000 rzutów orzeł wypadł 508 razy, czyli w 508/1000 = 0,508 wszystkich przypadków. Zaobserwowaliśmy, że badany przez nas iloraz jest ciągle bliski wartości 0,5. Znaleziona przez nas wielkość to częstość wypadania orła. Teraz mamy już pewne wyobrażenie o zaproponowanej grze.
Co jednak stałoby się, jeśli nie mielibyśmy możliwości przeprowadzenia doświadczenia? Chcielibyśmy mieć możliwość obliczenia prawdopodobieństwa wyrzucenia orła przed pierwszym rzutem. Możemy zauważyć, że są tylko dwa rezultaty: orzeł i reszka. Jeżeli moneta nie jest oszukana, tzn. obydwa rezultaty są jednakowo możliwe, orzeł powinien pojawić się w 1/2 = 0,5 możliwych przypadków. Obliczyliśmy prawdopodobieństwo zdarzenia bez konieczności przeprowadzania doświadczenia.
Definicja prawdopodobieństwa
Klasyczna
Geometryczna
Aksjomatyczna
1.Klasyczna definicja prawdopodobieństwa
(Laplace'a)
Sposób liczenia prawdopodobieństwa podał po raz pierwszy Pierre Simon de Laplace w roku 1812. Definicję tę nazywamy klasyczną:
Prawdopodobieństwem zajścia zdarzenia A nazywamy iloraz liczby zdarzeń sprzyjających zdarzeniu A do liczby wszystkich możliwych przypadków, zakładając, że wszystkie przypadki wzajemnie się wykluczają i są jednakowo możliwe.
Definicję tę można zapisać również w bardziej formalny sposób:
Oznaczmy zbiór wszystkich możliwych przypadków przez Ω. Elementami zbioru Ω są zdarzenia elementarne ω, zaś zbiór Ω to zbiór zdarzeń elementarnych. Zbiór zdarzeń sprzyjających A będzie w takim wypadku podzbiorem zbioru Ω: A ⊂ Ω.
Prawdopodobieństwo zajścia zdarzenia A możemy zapisać w postaci:
gdzie |A| oznacza liczbę elementów (moc) zbioru A, zaś |Ω| liczbę elementów (moc) zbioru Ω.
Przykład: Rzucamy sześcienną kostką. Jakie jest prawdopodobieństwo, że liczba oczek będzie większa od 5?
Odpowiedź: Zbiór zdarzeń elementarnych Ω = {1, 2, 3, 4, 5, 6}, zatem liczba możliwych zdarzeń |Ω| = 6. Zbiór zdarzeń sprzyjających A = {6}, liczba zdarzeń sprzyjających |A| = 1. Prawdopodobieństwo zajścia zdarzenia wynosi:
Problemy z definicją klasyczną
Definicja klasyczna pozwala obliczać prawdopodobieństwo w prostych przypadkach, jednak zawiera szereg wad: nie można jej stosować dla zbiorów nieskończonych, a przede wszystkim zawiera błąd logiczny. Zdarzenia elementarne muszą być jednakowo możliwe, co znaczy przecież to samo co jednakowo prawdopodobne. Okazało się więc, że w definicji użyliśmy pojęcia, które definiujemy.
2.Geometryczna definicja prawdopodobieństwa
Definicja klasyczna nie pozwala obliczać prawdopodobieństwa w przypadku, gdy zbiory A i Ω są nieskończone, jeśli jednak zbiory te mają interpretację geometryczną, zamiast liczebności zbiorów można użyć miary geometrycznej (długość, pole powierzchni, objętość).
Przykład: z przedziału [0,4] wybieramy losowo punkt. Jakie jest prawdopodobieństwo, że wybrany punkt będzie należał do przedziału [1,2]?
Odpowiedź: Długości przedziałów wynoszą odpowiednio: |[0,4]| = 4 i |[1,2]| = 1. Zatem prawdopodobieństwo opisanego zdarzenia wynosi:
3.Aksjomatyczna definicja prawdopodobieństwa (Kołmogorowa)
Prawdopodobieństwem nazywamy dowolną funkcję
o wartościach rzeczywistych, określoną na podzbiorze zbioru zdarzeń elementarnych
, spełniającą warunki:
(A1)
dla każdego
;
(A2)
;
(A3) Jeśli
oraz
dla
, to
Warunki (A1-A3) zostały sformułowane przez Kołmogorowa w roku 1933 jako aksjomaty teorii prawdopodobieństwa.
Andriej Kołmogorow
Andriej Kołmogorow pracujący nad wykładem
Andriej Nikołajewicz Kołmogorow, ros. Андре́й Никола́евич Колмого́ров (ur. 25 kwietnia 1903, zm. 20 października 1987) - rosyjski matematyk, twórca współczesnej teorii prawdopodobieństwa. Pracował nad rozwojem topologii, logiki i teorii złożoności obliczeniowej, znany jest również z wyników w analizie harmonicznej i mechanice klasycznej. Laureat wielu nagród, m.in. Nagrody Wolfa w matematyce w 1980.
Studiował na Uniwersytecie Moskiewskim, który ukończył w 1925. Przez kolejne 4 lata kontynuował tam badania naukowe, głównie pod kierunkiem Nikołaja Łuzina i doktoryzował się w 1929. Został zatrudniony na Uniwersytecie Moskiewskim, gdzie mianowano go profesorem w 1931.
Matematyczny model doświadczenia losowego to trójka
gdzie
jest prawdopodobieństwem, określonym na pewnym podzbiorze
zbioru zdarzeń elementarnych
. Trójkę tę nazywamy przestrzenią probabilistyczną.
Prawdopodobieństwo - funkcja P(X), która przyporządkowuje każdemu elementowi zbioru zdarzeń losowych pewną nieujemną wartość rzeczywistą i ma następujące własności:
P(A1 ∪ ... ∪ An ∪ ... ) = P(A1) + ... + P(An) + ...
Wartość P(X) nazywa się prawdopodobieństwem zdarzenia X.
P(A) ≥ 0
P(Ø) = 0 (UWAGA: odwrotna implikacja nie jest prawdziwa - P(A)=0 nie implikuje A=Ø)
A ⊂ B ⇒ P(A) ≤ P(B)
P(A) ≤ 1
A ⊂ B ⇒ zdarzenie warunkowe P(B|A) = 1
P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
Własności wykorzystywane przy obliczaniu prawdopodobieństwa:
Działania jak na zbiorach, np.
![]()
![]()
;
Zasada iloczynu (drzewo prawdopodobieństw):
![]()
dla zdarzeń niezależnych;
Pomimo że wynik pojedynczego rzutu monetą lub kością do gry często z praktycznego punktu widzenia można uważać za nieprzewidywalny, jeżeli eksperyment taki powtórzony zostaje wielokrotnie, mogą pojawić się pewne prawidłowości i wzory statystyczne, które można badać i przewidzieć - kolejne wykłady!!!
Wiedza do przyswojenia:
zdarzenia losowe - rodzaje i działania;
definicje i aksjomaty prawdopodobieństwa;
matematyczny model doświadczenia losowego;
wiadomości z kombinatoryki z I roku.
Wyszukiwarka
Podobne podstrony:
ZARZ SRODOWISKIEM wyklad 1a
Audyt personalny 1a stud
1a wz2id 18643
II, rzis analityczny 1A Likpol
L1-1a, Ratownictwo Medyczne, Materiały ze studiów, Medycyna Ratunkowa
praca-magisterska-7092, 1a, prace magisterskie Politechnika Krakowska im. Tadeusza Kościuszki
praca-magisterska-7091, 1a, prace magisterskie Politechnika Krakowska im. Tadeusza Kościuszki
2 1a
BLOK 1a 2 3 id 90304 Nieznany
04 1a LICZNIKI XBK KATALOGid 4946
Cwiczenia z ochrony gleby cz 1a Nieznany
8 6 1a
praca-magisterska-6927, 1a, prace magisterskie Politechnika Krakowska im. Tadeusza Kościuszki
praca-magisterska-6888, 1a, prace magisterskie Politechnika Krakowska im. Tadeusza Kościuszki
1a-.Starożytność, PRAWO UŁ, I rok, Prawo rzymskie
więcej podobnych podstron