Piotr Grzybowski Gdańsk 2000.01.21

Telekomunikacja sem.V, gr.II

Laboratorium cyfrowego przetwarzania sygnałów.

Filtry cyfrowe.

Cyfrowa obróbka sygnału polega na wykonywaniu operacji matematycznych na kolejnych próbkach, co przy pomocy odpowiednich algorytmów obliczeniowych pozwala między innymi na filtrację sygnału. Mówimy wtedy o filtracji cyfrowej z zastosowaniem filtrów cyfrowych.

Filtry cyfrowe pozwalają na realizację wszystkich filtrów realizowanych dotychczas drogą analogową, ponadto można uzyskać charakterystyki filtrów cyfrowych, których stworzenie przy zastosowaniu filtrów analogowych mogłoby się okazać bardzo trudne. Kolejną przewagą filtrów cyfrowych nad analogowymi jest możliwość dowolnej modyfikacji ich charakterystyki w trakcie filtracji, która sprowadza się do zmiany odpowiednich współczynników filtru. Można w ten sposób łatwo tworzyć filtry adaptacyjne, tzn. takie, których charakterystyka ulega zmianie w zależności od nadchodzącego sygnału.

Istnieją dwa podstawowe typy filtrów cyfrowych:

FIR - filtr o skończonej odpowiedzi impulsowej (Finite Impulse Response)

IIR - filtr o nieskończone odpowiedzi impulsowej (Infinite Impulse Response)

Zasadnicza różnica pomiędzy tymi filtrami polega na tym, że do obliczenia kolejnej próbki za pomocą filtru FIR wykorzystuje się próbki wcześniej poddawane filtracji (w ilości zależnej od rzędu filtru), oraz próbkę bieżącą. W przypadku filtru typu IIR dodatkowo brane pod uwagę są próbki wcześniej filtrowane.

x[n] y[n]

W przypadku filtrów typu FIR filtrowanie odbywa się według wzoru:

Po dokonaniu transformacji Z powyższego równania można otrzymać transmitancję filtru:

Filtracja typu FIR polega na pomnożeniu próbek wejściowych bieżącej i wcześniejszych przez

odpowiednie współczynniki oznaczone jako b0-bN, oraz ich dodanie. Tak otrzymana suma jest kolejną

przefiltrowaną próbką y(n). Wartość N oznacza rząd filtru i ilość współczynników.

W przypadku filtrów typu IIR przy obliczaniu kolejnej próbki wyjściowej uwzględnia się również poprzednie próbki wyjściowe.

Filtracja odbywa się wg wzoru:

Po dokonaniu transformacji Z powyższego równania można otrzymać transmitancję filtru:

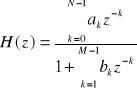
Jako przykład został poniżej omówiony telewizyjny filtr cyfrowy - korektor apertury na w.cz. Jest to wersja najprostsza - FIR o długości 3 ( rzędu 2 - go ) .

x[ n ] y[ n ]

-1/4 1/2 -1/4 k≥0

Dla danego filtru :

1. równanie różnicowe

2. odpowiedź impulsowa

3. transmitancje

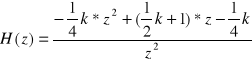
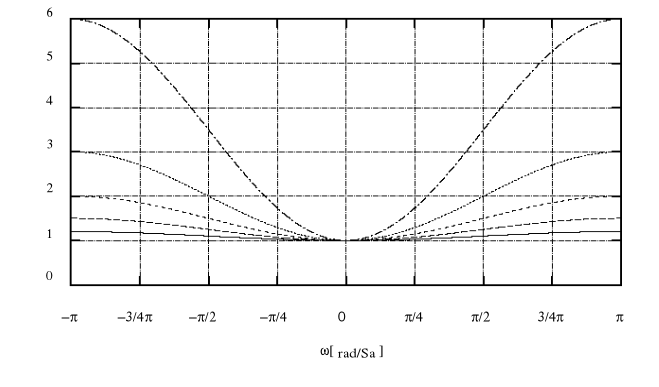
Rodzina charakterystyk analizowanego filtru przy zmianie parametru k ( skala liniowa ).

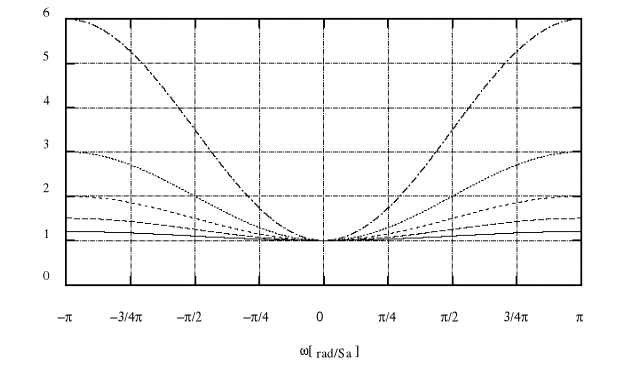
|H( e^j ) |

k = 0.2 k = 0.5 - - - - - k = 1.0 - - - - - k = 2.0 -------- k = 5.0 . . .

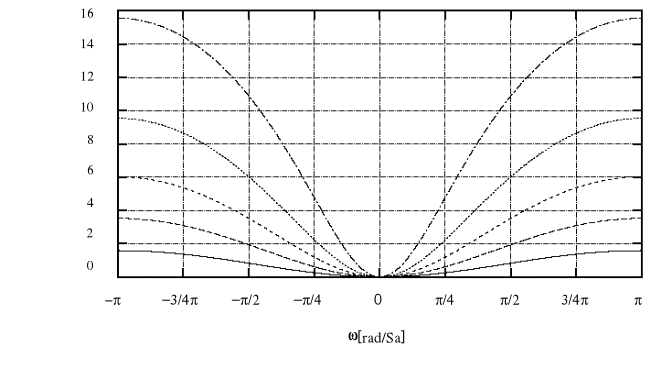
Rodzina charakterystyk analizowanego filtru przy zmianie parametru k ( skala decybelowa).

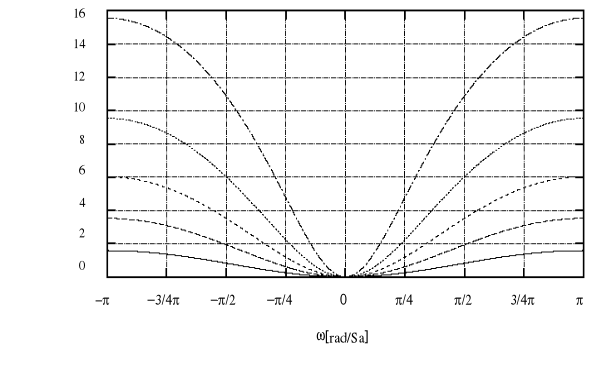
|H( e^j ) |

[ dB ]

k = 0.2 k = 0.5 - - - - - k = 1.0 - - - - - - k = 2.0 --------- k =5.0 . .

Jak łatwo zauważyć na podstawie powyższej rodziny charakterystyk filtr nie zmienia amplitudy niskich częstotliwości, natomiast wzmacnia częstotliwości wysokie. Wartość wzmocnienia zależy od parametru k i dla k rosnącego wzmocnienie rośnie.

Omówiony powyżej filtr jest filtrem typu FIR. W ogólności filtry te mogą mieć dokładnie liniową charakterystykę fazową. Nie wnoszą wtedy zniekształceń fazowych do przetwarzanego sygnału, co jest bardzo ważne w przetwarzaniu audio, video, transmisji danych. Z kolei charakterystyki fazowe filtrów IIR są silnie nieliniowe, zwłaszcza na krańcach pasm.

Filtry FIR wymagają niestety więcej współczynników by uzyskać ostre zbocza charakterystyki amplitudowej. Wymagają one na skutek tego dłuższego czasu przetwarzania i większej pamięci przy tej samej specyfikacji charakterystyki amplitudowej.

Filtry analogowe można łatwo przeprojektować w filtry IIR im równoważne ( tj. o podobnej specyfikacji ). Niestety nie można tego uczynić z filtrami FIR, które nie mają odpowiedników analogowych. Można za to przy pomocy filtrów FIR łatwiej syntezować filtr o dowolnie zadanej charakterystyce częstotliwościowej.

Porównując filtry cyfrowe i analogowe dostrzegamy zarówno wady i zalety obu tych rodzajów filtrów.

Zalety filtrów cyfrowych ( w porównaniu z analogowymi ):

1. gwarantowana dokładność zależna jedynie od liczby bitów. Dokładność osiągana za pomocą filtrów analogowych jest ograniczona. Maksymalne tłumienie zaporowe osiągane w filtrach aktywnych wynosi ok. 60 - 70 dB, a w filtrach cyfrowych może być dużo większe.

2. perfekcyjna powtarzalność charakterystyk - nie ma zmian termicznych na skutek starzenia, stąd nie ma potrzeby kalibracji okresowej

3. lepsze charakterystyki nieosiągalne w filtrach analogowych np. liniowa charakterystyka fazowa

4. większa elastyczność - charakterystyki częstotliwościowe można dostrajać używając programowalnych procesorów lub je modyfikować bez modyfikacji sprzętu ( przeprogramowanie )

5. możliwość uzyskania filtrów cyfrowych o większej niezawodności, mniejszych wymiarach, niższej cenie i niższym poborze mocy

6. możliwość używania ich do przetwarzania sygnałów o bardzo niskich częstotliwościach, gdzie filtry analogowe są niepraktyczne. Mogą pracować w szerokim zakresie częstotliwości przy zmianie jedynie częstotliwości próbkowania sygnału.

Wady filtrów cyfrowych ( w porównaniu z analogowymi ):

1. ograniczona szybkość. Maksymalna szerokość pasma sygnałów przetwarzanych przez filtry cyfrowe w czasie rzeczywistym jest dużo mniejsza niż dla filtrów analogowych. Głównym ograniczeniem jest szybkość konwerterów ADC i DAC limitująca maksymalną częstotliwość sygnałów przetwarzanych przez filtr. Ponadto szybkość pracy filtru cyfrowego zależy od szybkości procesora, liczby działań arytmetycznych algorytmu filtracji rosnąca ze wzrostem złożoności ( rzędu ) filtru.

2. długi czas projektowania i realizacji sprzętowej w porównaniu z filtrami analogowymi. Jednak raz zaprojektowany filtr cyfrowy można użyć do różnych typów filtracji i różnych zadań CPS z małymi tylko modyfikacjami.

Z^-1

Z^-1

Σ

Σ

Σ

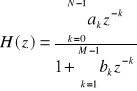
h[n]

---