I. Cześć teoretyczna (najważniejsze informacje dotyczące badanego zagadnienia).

Poniższe ćwiczenia mają na celu pomiary w układach szeregowych, równoległych i mieszanych rezystorów, aby dowieść prawdziwość praw Kirchhoffa. Szczególnie dotyczy to pierwszego prawa dla układu równoległego i mieszanego, oraz drugiego prawa dla układu szeregowego i mieszanego.

W elektrotechnice oporem nazywamy stosunek napięcia do natężenia w słownictwie powszechnym zwany rezystancją. Rezystancja charakteryzuje każdy przepływ prądu przez przewodnik lub odbiornik. Jest oczywiste, że im większa jest długość przewodu, tym większa proporcjonalnie droga jaką muszą przebyć elektrony swobodne w przewodzie, a wiec większy opór stawia przewód przepływowi prądu elektrycznego. Jeżeli zastosujemy przewód tej samej długości ale o większym przekroju opór będzie mniejszy. Opornikiem albo rezystorem nazywamy element obwodu elektrycznego wykonany celowo do potrzebnej rezystancji. Każde urządzenie elektryczne stawia opór który należy uwzględniać projektowania obwodów elektrycznych.

Opór elektryczny jest to wielkość charakteryzująca element przewodzący (przewodnik). Miarą rezystancji w przypadku prądu stałego - jest stosunek napięcia elektrycznego U między jego końcami do natężenia I płynącego przezeń prądu elektrycznego. R = U/I (prawo Ohma). Opór ten, zwany oporem elektrycznym czynnym (omowym) lub rezystancją, w przypadku elementu przewodzącego wykonanego z jednorodnego materiału izotropowego o stałym przekroju poprzecznym S i długości d jest równy R =ρd/S, gdzie ρ-opór elektryczny właściwy, zw. też rezystywnością , charakteryzuje właściwości elektryczne materiału przewodnika. Wartość oporu elektrycznego właściwego dla różnych materiałów jest różna - najmniejsza dla metali (10^-8-10^-4 · m), największa dla dielektryków (>10⁷ · m), pośrednia dla półprzewodników - i w różnym stopniu zależy od temperatury, zanieczyszczeń, składu chemicznego, naprężeń mechanicznych i innych czynników (np. padającego światła w przypadku półprzewodników). W analizie obwodów elektrycznych, w których zmiany napięć i prądów mają charakter sinusoidalny, wprowadza się pojęcie oporu elektrycznego pozornego (zespolonego) Z, zwanego też impedancją (zespoloną), zdefiniowanego (zgodnie z prawem Ohma dla wartości skutecznych zespolonych) zależnością Z = U/I . W ogólnym przypadku Z = R + jX, a jej moduł |Z|=R²+X², przy czym R jest oporem elektrycznym czynnym (rezystancją), natomiast X jest oporem elektrycznym biernym nazywanym też reaktancją. W szczególnym przypadku - szeregowo połączonych elementów o indukcyjności L i pojemności C - wypadkowa reaktancja wynosi X = L - (  pulsacja prądu zmiennego). Wyrażenie L jest zwane oporem elektrycznym biernym indukcyjnym (reaktancją indukcyjną, induktancją), a 1/C — oporem elektrycznym biernym pojemnościowym (reaktancją pojemnościową, kapacitancją ). Do pomiaru oporu elektrycznego używa się omomierza, megaomomierza, mostka elektrycznego, logometru, woltomierza i amperomierza, kompensatora elektrycznego itp. Jednostką oporu elektrycznego jest Ohm Ω.

II. Część praktyczna.

1)Treść zadania:

a) Połączenie szeregowe rezystorów :

Dla trzech wartości napięcia zasilającego zmierzyć spadki napięcia na rezystorach oraz prąd płynący w obwodzie. Obliczyć rezystancję zastępczą na podstawie pomiarów (R_z) oraz na podstawie parametrów znamionowych rezystorów (R_zobl). Na podstawie pomiarów obliczyć błąd względny i bezwzględny wielkości mierzonych.

R= U/I (z prawa Ohma)

R_z=R1+R2+R3 [Ω]

Uc _obl=U1+U2+U3 [V]

R_z'=U_{c obl}/I_obl [Ω]

b) Połączenie równoległe rezystorów :

Dla trzech wartości napięcia zasilającego zmierzyć spadki napięcia na rezystorach oraz prąd płynący w obwodzie. Obliczyć rezystancję zastępczą na podstawie pomiarów (R_z) oraz na podstawie parametrów znamieniowych rezystorów (R_zobl). Na podstawie pomiarów obliczyć błąd względny i bezwzględny wielkości mierzonych.

Ic _obl=I1+I2+I3 [ A]

R=U/I

R_obl=1/R1+1/R2+1/R3 [Ω]

R_obl'=U/I_obl [Ω]

c) Połączenie mieszane rezystorów :

Dla trzech wartości napięcia zasilającego zmierzyć spadki napięcia na rezystorach oraz prąd płynący w obwodzie. Obliczyć rezystancję zastępczą na podstawie pomiarów (R_z) oraz na podstawie parametrów znamieniowych rezystorów (R_zobl). Na podstawie pomiarów obliczyć błąd względny i bezwzględny wielkości mierzonych.

Uc=U1+U2 [V]

I_obl=I1+I2 [A]

R_z= Uc/I3 [Ω]

Rz _obl= [R1*R2/R1+R2] + R3 [Ω]

2)Sprawdzane przedmioty i wymiary (szkic mierzonego przedmiotu i wymiary symbolowe, schemat urządzenia itp.):

a) Połączenie szeregowe rezystorów :

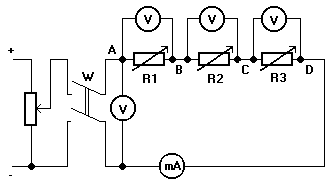
b) Połączenie równoległe rezystorów :

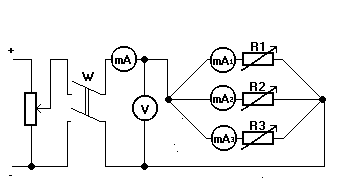
c) Połączenie mieszane rezystorów :

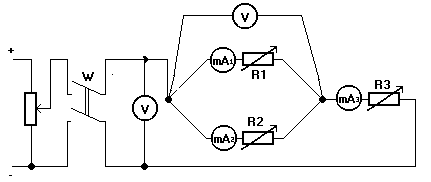
3)Sprzęt mierniczy:

• Zasilacz TYP ZT-980-2M

• Amperomierz- 60mV LM1 PRLT104 370546/73

• Amperomierz - 60mV LM1 PRLT104 3507150/74

• Amperomierz- 60mV LM1 PRLT104 3708057/73

• Amperomierz- 60mV LM1 PRLT104 3707581/73

• Woltomierz- 3mA LM1 PRLT104 2303590/72

• Woltomierz - 3mA LM1 PRLT104 2103496/73

• Woltomierz- 3mA LM1 PRLT104 3507357/74

• Woltomierz- 3mA LM1 PRLT104 3507349/74

• Opornik dekadowy R=10x10 Ω T_max=300mA kl.01

• Opornik - 10 Ω

• Opornik - 20 Ω - 3A

4)Wyniki pomiarów (tabela zestawieniowa wyników):

a) Połączenie szeregowe rezystorów :

	Woltomierz U1			Woltomierz U2			Woltomierz U3			Amperomierz A			Woltomierz Uc			Obliczenia
	Cu	α	U	Cu	α	U	Cu	α	U	Ca	α	I	Cu	α	U	Uc obl.	R	Rz
	V/dz	α	V	V/dz	α	V	V/dz	dz	V	V/dz	α	A	V/dz	α	V	V	Ω	Ω
1. 2. 3.	0,5 0,5 0,5	7 10 14	3,5 5 7	0,5 0,5 0,5	7 10 15	3,5 5 7,5	0,5 0,5 0,5	14 20 29	7 10 14,5	0,01 0,01 0,01	15 20 30	0,15 0,2 0,3	1 1 1	15 20 24	15 20 24	14 20 29	100 100 80	93,3 100 96,6
Śr	0,5	10,3	5,16	0,5	10,66	533	0,5	21	10,5	0,01	21,66	0,21	1	19,66	19,66	21	93,3	96,63

b) Połączenie równoległe rezystorów :

	Woltomierz			Amperomierz I1			Amperomierz I2			Amperomierz I3			Amperomierz I			Obliczenia
	Cu	α	U	Ca	α	I	Ca	α	I	Ca	α	I	Ca	α	I	Iobl	R	Robl
	V/dz	Dz	V	A/dz	dz	A	A/dz	dz	A	A/dz	Dz	A	A/dz	dz	A	A	Ω	Ω
1. 2. 3.	1 1 1	4 7 9	4 7 9	0,01 0,01 0,01	11 20 27	0,11 0,2 0,27	0,01 0,01 0,01	19 28 37	0,19 0,28 0,37	0,01 0,01 0,01	10 14 19	0,1 0,14 0,19	0,01 0,01 0,01	24 46 62	0,24 0,46 0,62	0,4 0,62 0,83	16,6 15,2 14,5	10 11,29 10,84
Śr	1	6,66	6,66	0,01	19,33	0,19	0,01	28	0,28	0,01	14,3	0,14	0,01	44	0,44	0,62	15,4	10,71

c) Połączenie mieszane rezystorów :

	Amperomierz I3			Amperomierz I2			Amperomierz I1			Woltomierz V1			Woltomierz V2			Obliczenia			Obliczenia
	Ca	α	I	Ca	α	I	Ca	α	I	Cu	α	U	Cu	α	U	Uc	Iobl	Rz	Robl
	A/dz	α	A	A/dz	α	A	A/dz	α	A	V/dz	α	V	V/dz	α	V	V	A	Ω	Ω
1. 2. 3.	0,01 0,01 0,01	30 34 59	0,3 0,34 0,59	0,01 0,01 0,01	11 12 23	0,11 0,12 0,23	0,01 0,01 0,01	5 7 21	0,05 0,07 0,21	1 1 1	12 16 21	12 16 21	1 1 1	2 3 5	2 3 5	14 19 26	0,45 0,58 0,91	46,66 55,88 44,06
Śr	0,01	41	0,41	0,01	15,3	0,15	0,01	11	0,11	1	16,3	16,3	1	3,3	3,3	19,6	0,64	48,86

5)Obliczenia:

a) Połączenie szeregowe rezystorów :

R=U/I=15V/0,15A=100Ω

R=U/I=20V/0,2A=100Ω

R=U/I=24V/0,3A=80Ω

U_cobl=U1+U2+U3=3,5V+3,5V+7V=14V

U_cobl=U1+U2+U3=5V+5V+10V=20V

U_cobl=U1+U2+U3=7V+7,5V+14,5V=29V

Rz'=U_cobl/I=14V/0,15A=93,3Ω

Rz'=U_cobl/I=20V/0,2A=100Ω

Rz'=U_cobl/I=29V/0,3A=96,6Ω

b) Połączenie równoległe rezystorów :

R=U/I=4V/0,24A=16,67Ω

R=U/I=7V/0,46A=15,21Ω

R=U/I=9V/0,62A=14,51Ω

I_cobl=I1+I2+I3=0,11A+0,19A+0,1A=0,4A

I_cobl=I1+I2+I3=0,2A+0,28A+0,14A=0,62A

I_cobl=I1+I2+I3=0,27A+0,37A+0,19A=0,83A

Rz'=U_cobl/I=4V/0,4A=10Ω

Rz'=U_cobl/I=7V/0,62A=11,29Ω

Rz'=U_cobl/I=9V/0,83A=10,84Ω

c) Połączenie mieszane rezystorów :

U_c=U1+U2=12V+2V=14V

U_c=U1+U2=16V+3V=19V

U_c=U1+U2=21V+5V=26V

I_obl=I1/I2=0,05A/0,11A=0,45A

I_obl=I1/I2=0,07A/0,12A=0,58A

I_obl=I1/I2=0,21A/0,23A=0,91A

R_z=U_c/I3=14V/0,3A=46,66Ω

R_z=U_c/I3=19V/0,34=55,88Ω

R_z=U_c/I3=26V/0,59A=44,06Ω

6)Uwagi i wnioski końcowe:

W powyższym ćwiczeniu obliczone wartości napięcia pokrywają się z wartością zmierzoną w granicach klasy dokładności mierników oraz rezystorów. Dowodzi to prawdziwość drugiego prawa Kirchhoffa, które mówi, że w dowolnym oczku obwodu prądu stałego suma algebraiczna napięć odbiornikowych, występujących na rezystancjach rozpatrywanego oczka oraz suma algebraiczna napięć źródłowych jest równa zeru. Wartość wypadkowa rezystancji obwodu dla rezystorów połączonych szeregowo jest równa sumie rezystancji.

W tym ćwiczeniu dowodzimy prawdziwość pierwszego prawa Kirchhoffa, które mówi iż dla każdego węzła obwodu elektrycznego suma prądów dopływających jest równa sumie prądów odpływających od węzła. Wartość rezystancji wypadkowej rezystorów połączonych równolegle jest równa wartości [R1*R2/R1+R2].

Dla mieszanego połączenia rezystancji wartość wypadkowej rezystancji zastępczej jest kombinacją wzorów na połączenie równoległe i szeregowe rezystorów. W powyższym ćwiczeniu możemy dowieść prawdziwość pierwszego u drugiego prawa Kirchhoffa. Spadek napięcia na rezystorach połączonych równolegle jest jednakowy dla obu rezystorów, lecz wartości prądów przez nie płynące są różne. W przypadku połączenia szeregowego spadki napięć na poszczególnych rezystancjach jest inny, równy jest natomiast prąd przez nie płynący.

Rezystancja równoważna równa się sumie połączonych rezystancji ( R= 1R+2R+...), odwrotność rezystancji równoważnej równa się sumie połączonych rezystancji ( 1/R=1/1R+1/2R+...). Natężenie prądu przepływającego jest jednakowe w odbiornikach i źródle I=1I=2I=...W każdym odbiorniku płynie prąd o tym samym natężeniu. Całkowite napięcie rozkłada się wprost proporcjonalnie na poszczególne opory czyli U1: U2:U3= R1:R2:R3. Napięcie na wszystkich oporach jest jednakowe (wspólne) w połączeniu równoległym U1=U2=U3=U. Rezystancja przewodu jest wprost proporcjonalna do jego długości, a odwrotnie proporcjonalna do jego przekroju. Opornikiem albo rezystorem nazywamy element obwodu elektrycznego wykonany celowo dla uzyskania potrzebnej rezystancji odwrotność rezystancji nazywamy konduktancją albo przewodnością elektryczną oznaczamy literą G=1/R jednostką konduktancji jest simens.

Michał Królewski ZPiU

5

---