Krótki wstęp teoretyczny.

Jeżeli do zacisków 1-2 układu złożonego z szeregowo połączonych: rezystancji R, pojemności C i indukcyjności L (rysunek) przyłożymy siłę elektromotoryczną sinusoidalnie zmienną:
E=Eosint,
(Eo - amplituda siły elektromotorycznej), to w układzie popłynie prąd sinusoidalnie zmienny o natężeniu
I=Iosin(t-),
gdzie: Io - amplituda natężenia prądu
 - przesunięcie fazowe między natężeniem prądu a siłą elektromotoryczną

Można wykazać, że między Eo a Io zachodzi związek:
Io=Eo/Z. który można też przedstawić jako Isk=Esk/Z

Powyższa zależność przedstawia prawo Ohma dla prądu zmiennego. Łatwo zauważyć, że Z jest odpowiednikiem R w prawie Ohma dla prądu stałego. Z nazywamy zawadą.

Dla układu z rysunku, korzystając z II prawa Kirchhoffa otrzymujemy:
IR + U = E + Es
gdzie: U - napięcie na kondensatorze
Es - siła elektromotoryczna samoindukcji Es= - L dI/dt.

Po wykonaniu kilku przekształceń otrzymamy wzór:
Io=Eo/(R2+(L-1/C)2)

Jeżeli go porównamy z poprzednim wzorem na Io, otrzymamy następujący wzór na zawadę:
Z=(R2+(L-1/C)2)
wymiarem zawady są Ohmy - pod pierwiastkiem mamy:
2 =V*s/C
(H/s)2 H=V*s2/C, czyli H/s=V*s/C
(s/F)2 F=C/V, czyli s/F=V*s/C

Jak widać powyżej, każdy z członów równania pod pierwiastkiem ma ten sam wymiar.Przesunięcie fazowe  możemy obliczyć korzystając ze wzoru :
tg=(L-1/C)/R

Ponieważ przy zagadnieniach technicznych posługujemy się częstotliwością zwykłą, a nie kołową,  we wzorach zastępujemy przez 2f. Ze względu zaś na mierzone wielkości
wzór Io=Eo/Z zastępujemy przez Isk=Esk/Z.

Wzory:

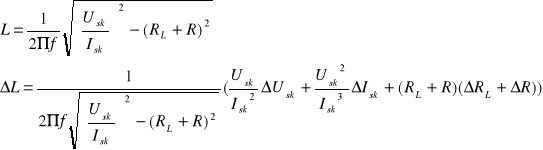
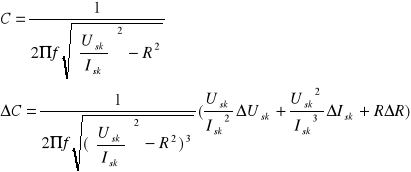
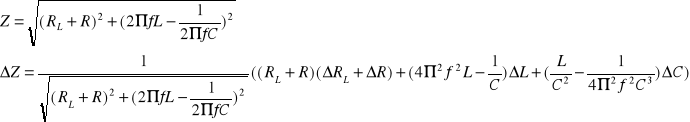
Błędy pomiarów obliczyłem korzystając z metody różniczki zupełnej.

Obliczenia zawady:

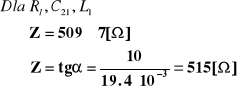
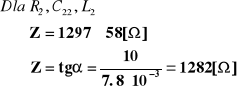
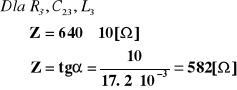
Dyskusja błędów i wnioski:

Wykonane doświadczenie dowiodło słuszności prawa Ohma dla prądu przemiennego. O prawdziwości tego prawa przekonują nas dwa elementy naszego doświadczenia. Otóż jak łatwo zauważyć na zamieszczonym wykresie istnieje liniowa zależność pomiędzy napięciem i natężeniem skutecznym prądu, co więcej obserwujemy dużą zbieżność wyników obliczeń zawady układu z wartością tangensa nachylenia wykreślonych prostych U=f(I). Wyjątkowo tylko dla trzeciego układu RLC wartość tangensa nie zawiera się w przedziale błędu wartości zawady obliczonej ze wzoru (przypuszczalnie wynika to z niedokładności wykonanego wykresu).

Otrzymane niskie wartości błędu względnego świadczą o dużej dokładności pomiaru. Wadą układu pomiarowego, która na pewno wpłynęła na dokładność wyników było użycie niewłaściwych mierników. Dla wielu punktów pomiarowych byliśmy zmuszeni dokonywać odczytu w sytuacji, gdy wskazówka przyrządu nie przekroczyła jeszcze 2/3 skali, a nawet czasami 1/2 skali. Niestety nie można było zmienić zakresu na niższy. Dla uzyskania większej dokładności możnaby zastosować mierniki cyfrowe. Jednakże w większości przypadków nie ma potrzeby zwiększania dokładności (np. w większości sprzętu elektronicznego stosuje się kondensatory z błędem względnym 5%).

Ze względu na swoją prostotę układy RLC znajdują wiele zastosowań. Dzięki nim można np. tak jak w doświadczeniu dokonywać pomiaru pojemności i indukcyjności. Istnieje wiele modyfikacji układu RLC, które są szeroko stosowane jako generatory, np generatory: Meissnera, Hartleya, Colpittsa, Clappa.

---