1. Zebranie obciążeń.
1.1. Określenie podstawowych danych liczbowych
- pole powierzchni płyty żelbetowej
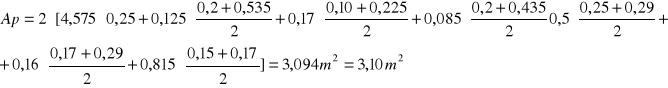
- pole powierzchni kap chodnikowych
![]()
1.2. Faza I
Materiał |
Obciążenie charakterystyczne [kN/m] |
|
Obciążenie obliczeniowe [kN/m] |
1.Płyta żelbetowa 3,10m2x28,0kN/m3 |
86,8 |
0,9 1,2 |
78,12 104,16 |
2. Deskowanie 12,66mx0,04mx6,0kN/m2 |
3,038 |
0,9 1,2 |
2,734 3,646 |
3.Dźwigary stalowe 5x[0,2x0,02+0,4x0,04+1,44x0,02]x78,5kN/m3 |
17,584 |
0,9 1,2 |
15,826 21,101 |
4. Stężenia 12% 17,584/m3 |
2,11 |
0,9 1,2 |
1,899 2,532 |
∑ |
109,232 |
|
98,579 131,348 |
Obciążenie przypadające na jeden dźwigar |
21,846 |
|
19,716 26,270 |
1.3. Faza II
Materiał |
Obciążenie charakterystyczne [kN/m] |
|
Obciążenie Obliczeniowe [kN/m] |
1.Kapy chodnikowe 1,10m2x27,0kN/m3 |
29,70 |
0,9 1,5 |
26,73 44,55 |
2. Papa termozgrzewalna 12,66mx0,01mx23,0kN/m3 |
2,912 |
0,9 1,5 |
2,621 4,367 |
3. Nawierzchnia chodnikowa 2x2,38x0,01x23,0kN/m3 |
1,095 |
0,9 1,5 |
0,985 1,642 |
4. Asfalt lany 7,0mx0,04mx23,0kN/m3 |
6,44 |
0,9 1,5 |
5,80 9,66 |
5. Beton asfaltowy 7,0x0,04x23,0kN/m3 |
6,44 |
0,9 1,5 |
5,80 9,66 |
6. Krawężniki 0,03m2x2x25,0kN/m3 |
1,500 |
0,9 1,5 |
1,350 2,250 |
7. Bariery i balustrady 0,5kN/m3x4 |
2,000 |
0,9 1,5 |
1,800 3,00 |
8. Zdjęte deskowanie |
-3,038 |
0,9 1,2 |
-2,734 -3,646 |
9.Ciężar wody w płycie - odparowanie |
-3,10 |
0,9 1,2 |
-2,79 -3,72 |
∑ |
43,949 |
|
39,554 52,739 |
Obciążenie przypadające na jeden dźwigar |
8,79 |
|
7,911 10,548 |
1.4.Obciążenie użytkowe
obciążenie taborem samochodowym
obciążenie rozłożone qo = 2,0 [kN/m2]
siły skupione Ko = 400 [kN]
nacisk na oś Po = 100 [kN]
współczynnik dynamiczny
![]()
![]()
- rozpiętość teoretyczna mostu
![]()
obciążenie pojazdem „K” (ze współczynnikiem dynamicznym)
obciążenie równomiernie rozłożone obliczeniowe
![]()
![]()
- współczynnik obciążeń równy 1,5
![]()
obciążenie skupione obliczeniowe
![]()
![]()
- współczynnik dynamiczny
![]()
- współczynnik obciążeń równy 1,5
![]()
obciążenie przypadające na oś obliczeniowe
![]()
![]()
obciążenie tłumem pieszych
![]()
![]()
![]()
- współczynnik obciążeń równy 1,3
Wstępne wymiarowanie
Schemat statyczny to ustrój swobodnie podparty, 3 przęsłowy o rozpiętości teoretycznej przęseł L=30,8m. Obciążenie taborem klasy B
Szerokość jezdni Ba = 6,5 + 2*0,5m = 7,5m
Szerokość chodników Bb = 2 * 1m
A. Płyta żelbetowa
Przyjęto wysokość płyty żelbetowej t=25cm
Pogrubienie nad dźwigarami stalowym średnio przyjęto 0,10cm
Klasa betonu B30
Rm = 17,3 MPa
Eb= 32,6 GPa
B. Dźwigar stalowy
Ilość dźwigarów głównych r= 5, rozstaw L = 2,4m
Wysokość środnika:
ho = (1/20 - 1/15)L
ho = (31,2/20 - 31,2/15)
ho = (1,54 - 2,053)
Przyjmuję ho = 2,0m
Grubość środnika:
tw = 2,0mm
Smukłość środnika:
λ= ho / tw
λ= 2000/20 = 100 <= 200
Szerokość półki górnej:
b1 = 200mm
Grubość półki górnej:
t1= 20mm
Szerokość półki dolnej:
b2= (0,2 *ho - 0,4*ho)
b2= (3,6 - 7,8)
Przyjęto b2= 600mm
Grubość półki dolnej:
t2= 30mm
2. Rozdział poprzeczny obciążenia metodą sztywnej poprzecznicy
b2=b4=2,4m; b1=b5=4,8m
Wzór ogólny : 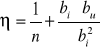
![]()
- liczba dźwigarów
![]()
bi,bu - odległość odpowiedniego dźwigara od środka przekroju
DŹWIGAR 1
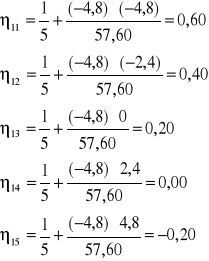
DŹWIGAR 2
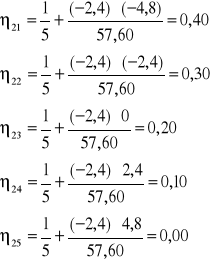
DŹWIGAR 4
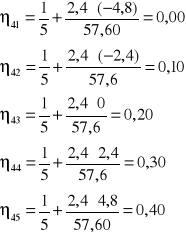
DŹWIGAR 5
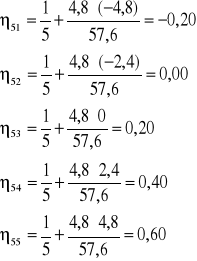
Obciążenie zmienne działające na dźwigary:
- dźwigar 5 (1)
- obciążenia obliczeniowe
obciążenie siłą skupioną od nacisku koła
![]()
![]()
obciążenie równomiernie rozłożone od taboru samochodowego
![]()
![]()
obciążenie równomiernie rozłożone od tłumu na chodniku
![]()
![]()
![]()
![]()
obciążenie siłą skupioną od nacisku koła
![]()
![]()
obciążenie równomiernie rozłożone od taboru samochodowego
![]()
![]()
obciążenie równomiernie rozłożone od tłumu na chodniku
![]()
![]()
![]()
![]()
- dźwigar 4 (2)
- obciążenia obliczeniowe
obciążenie siłą skupioną od nacisku koła
![]()
![]()
obciążenie równomiernie rozłożone od taboru samochodowego
![]()
![]()
obciążenie równomiernie rozłożone od tłumu na chodniku
![]()
![]()
![]()
![]()
- obciążenia charakterystyczne
obciążenie siłą skupioną od nacisku koła
![]()
![]()
obciążenie równomiernie rozłożone od taboru samochodowego
![]()
![]()
obciążenie równomiernie rozłożone od tłumu na chodniku
![]()
![]()
![]()
![]()
Wniosek: najbardziej obciążone są dźwigary skrajne 1 i 5
3. Obwiednie momentów zginających i sił poprzecznych w fazach od obciążeń stałych i ruchomych
3.1. Rozdział podłużny
3.2. Obliczenie momentów minimalnych i maksymalnych oraz sił poprzecznych
![]()
gdzie : p - pole powierzchni pod linia wpływu
q - obciążenie równomierne
l1 - rozpiętość przęsła skrajnego
Do dalszych obliczeń przyjęto dźwigar nr 1 gdyż jest on bardziej obciążony:
P=
68,68 kN
q = 6,760 kN/m
∑Ma = 0 →P * x - Rb * L = 0→ Rb= x/L
∑Mb= 0 → -P * ( L-x )+Ra * L = 0→ Ra= 1 -x/L
ŋmax = Ra * x, pole linii wpływu: pole Lw = 0,5 * L * ŋmax
Przęsło podzielono na 10 części
Wartość rzędnej LwM z lewej strony:
, gdzie a= 1,2m/ 2,4m/ 3,6m
Wartość rzędnej LwM z prawej strony
, gdzie b= 1,2m/ 2,4m/ 3,6m
Do obliczeń przyjęto cztery największe wartości z wyliczonych powyższymi wzorami rzędnych. Przy czym ŋmax = ŋ1. Obliczenia wykonano w arkuszu kalkulacyjnym
Linia wpływu momentu zginającego w pkt 1
X Є (0; 3,12)
Rzędne Lw [m]
ŋ1 = 2,808 ŋ2= 2,688 ŋ3 = 2,568 ŋ4 = 2,448 ∑ ŋ= 10,512
pole Lw = 43,805 m2
Faza I
Mmax = 26,270*43,805 = 1150,752 kNm
Mmin = 19,716 *43,805 = 863,655 kNm
Faza II - obciążenia stałe
Mmax = 10,548 * 43,805 = 462,053 kNm
Mmin = 7,911 * 43,805 = 346,540 kNm
Faza II - obciążenia zmienne
Mmax = 6,760 * 43,805 + 68,68 * 10,512 = 967,490 kNm
Suma
Mmax = 462,053 +967,490 = 1429,543 kNm
Mmin = 346,540 + 0 = 346,540 kNm
Linia wpływu momentu zginającego w pkt 2
X Є (0; 6,24)
Rzędne Lw [m]
ŋ1 = 4,99 ŋ2= 4,752 ŋ3 = 4,512 ŋ4 = 4,272 ∑ ŋ= 18,528
pole Lw = 77,875 m2
Faza I
Mmax = 26,270 * 77,875 = 2045,782 kNm
Mmin = 19,716 * 77,875 = 1535,387kNm
Faza II - obciążenia stałe
Mmax = 10,548 * 77,875 = 821,428kNm
Mmin = 7,911 * 77,875 = 616,071kNm
Faza II - obciążenia zmienne
Mmax = 6,760 * 77,875 + 68,68 * 18,528 = 1709,071kNm
Suma
Mmax = 821,428+1709,071= 2530,499 kNm
Mmin = 616,071+ 0 = 616,071 kNm
Linia wpływu momentu zginającego w pkt 3
X Є (0; 9,36)
Rzędne Lw [m]
ŋ1 = 6,55 ŋ2= 6,192 ŋ3 = 5,832 ŋ4 = 5,472 ∑ ŋ= 24,048
pole Lw = 102,211 m2
Faza I
Mmax = 26,270 * 102,211 = 2685,088 kNm
Mmin = 19,716 * 102,211 = 2015,196 kNm
Faza II - obciążenia stałe
Mmax = 10,548 * 102,211 = 1078,124 kNm
Mmin = 7,911 * 102,211 = 808,593 kNm
Faza II - obciążenia zmienne
Mmax = 6,760 * 102,211 + 68,68 * 24,048 = 2224,51 kNm
Suma
Mmax = 1078,124 + 2224,51 = 3302,634 kNm
Mmin = 808,593 + 0 = 808,593 kNm
Linia wpływu momentu zginającego w pkt 4
X Є (0; 12,48)
Rzędne Lw [m]
ŋ1 = 7,49 ŋ2= 7,008 ŋ3 = 6,528 ŋ4 = 6,048 ∑ ŋ= 27,072
pole Lw = 116,813 m2
Faza I
Mmax = 26,270 * 116,813 = 3068,672 kNm
Mmin = 19,716 * 116,813 = 2303,081 kNm
Faza II - obciążenia stałe
Mmax = 10,548 * 116,813 = 1232,141 kNm
Mmin = 7,911 * 116,813 = 924,106 kNm
Faza II - obciążenia zmienne
Mmax = 6,760 * 116,813 + 68,68 * 27,072 = 2514,041 kNm
Suma
Mmax = 1232,141 + 2514,041 = 3746,182 kNm
Mmin = 924,106 + 0 = 924,106 kNm
Linia wpływu momentu zginającego w pkt 5
X Є (0; 15,6)
Rzędne Lw [m]
ŋ1 = 7,80 ŋ2= 7,200 ŋ3 = 6,600 ŋ4 = 6,000 ∑ ŋ= 27,600
pole Lw = 121,68 m2
Faza I
Mmax = 26,270 * 121,68 = 3196,534 kNm
Mmin = 19,716 * 121,68 = 2399,043 kNm
Faza II - obciążenia stałe
Mmax = 10,548 * 121,68 = 1283,481 kNm
Mmin = 7,911 * 121,68 = 962,610 kNm
Faza II - obciążenia zmienne
Mmax = 6,760 * 121,68 + 68,68 * 27,600 = 2577,584 kNm
Suma
Mmax = 1283,481 + 2577,584 = 3861,065 kNm
Mmin = 962,610 + 0 = 962,610 kNm
Linie wpływu sił poprzecznych
∑Ma = 0 →P * x - Rb * L = 0→ Rb= x/L
∑Mb= 0 → -P * ( L-x )+Ra * L = 0→ Ra= 1 -x/L
Część ujemna LwT:
ηmin = - (x/L), pole = - 0,5 * x * ηmin
Część dodatnia LwT:
ŋmax = 1- (x/L), pole = 0,5 * (L-x ) * ŋmax
Rzędna linii wpływy T
,
, gdzie b= 1,2m/ 2,4m/ 3,6m
Obliczenia wykonano w arkuszu kalkulacyjnym
Linia wpływu tnącej w pkt 0
X = 0
Rzędne dodatnie Lw [m]
ŋ1 = 1 ŋ2=0,961 ŋ3 = 0,923 ŋ4 = 0,885 ∑ ŋ= 3,769
pole Lw = 15,600
Rzędne ujemne Lw [m]
ŋ1 = 0 ŋ2=0 ŋ3 = 0 ŋ4 = 0 ∑ ŋ= 0
pole Lw = 0
Faza I
Tmax = 26,270 *15,600 + 19,716 * 0= 467,667kN
Tmin = 19,716 * 15,600 + 26,270 * 0= 307,569 kN
Faza II - obciążenia stałe
Tmax = 10,548 * 15,600 + 7,911 * 0 = 164,549 kN
Tmin = 7,911 * 15,600 + 10,548 * 0 = 123,411 kN
Faza II - obciążenia zmienne
Tmax = 6,760 * 15,600 + 68,68 * 3,769= 346,309 kN
Tmin = 6,760 * 0 + 68,68 * 0= 0
Suma
Tmax = 164,549 +346,309 = 510,858 kN
Tmin = 123,411 + 0 = 123,411 kN
Linia wpływu tnącej w pkt 1
X Є (0; 3,12)
Rzędne dodatnie Lw [m]
ŋ1 = 0,9 ŋ2=0,862 ŋ3 = 0,823 ŋ4 = 0,785 ∑ ŋ= 3,369
pole Lw = 12,64 m2
Rzędne ujemne Lw [m]
ŋ1 = -0,1 ŋ2=-0,062 ŋ3 = -0,023 ŋ4 = 0,015 ∑ ŋ= -0,169
pole Lw = -1,404 m2
Faza I
Tmax = 26,270 *12,64 + 19,716 * -1,404= 304,266 kN
Tmin = 19,716 * 12,64 + 26,270 * -1,404= 212,248 kN
Faza II - obciążenia stałe
Tmax = 10,548 * 12,64 + 7,911 * -1,404 = 122,177 kN
Tmin = 7,911 * 12,64 + 10,548 * -1,404 = 85,154 kN
Faza II - obciążenia zmienne
Tmax = 6,760 * 12,64 + 68,68 * 3,369= 302,236 kN
Tmin = 6,760 * -1,404 + 68,68 * -0,169= -19,494
Suma
Tmax = 133,284 +302,236 = 435,521 kN
Tmin = 85,154 + (-19,494) = 65,66 kN
Linia wpływu tnącej w pkt 2
X Є (0; 6,24)
Rzędne dodatnie Lw [m]
ŋ1 = 0,8 ŋ2=0,762 ŋ3 = 0,723 ŋ4 = 0,685 ∑ ŋ= 2,969
pole Lw = 9,984 m2
Rzędne ujemne Lw [m]
ŋ1 = -0,2 ŋ2=-0,162 ŋ3 = -0,123 ŋ4 = -0,085 ∑ ŋ= -0,569
pole Lw = -2,496 m2
Faza I
Tmax = 26,270 *9,984+ 19,716 * -2,496= 213,068 kN
Tmin = 19,716 * 9,984+ 26,270 * -2,496= 131,275 kN
Faza II - obciążenia stałe
Tmax = 10,548 * 9,984+ 7,911 * -2,496= 85,565 kN
Tmin = 7,911 * 9,984+ 10,548 * -2,496= 52,656 kN
Faza II - obciążenia zmienne
Tmax = 6,760 * 9,984+ 68,68 * 2,969= 259,897 kN
Tmin = 6,760 * -2,496+ 68,68 * -0,569= -53,087
Suma
Tmax = 85,565 +259,897 = 345,462 kN
Tmin = 52,656 + (-53,087) = -0,432 kN
Linia wpływu tnącej w pkt 3
X Є (0; 9,36)
Rzędne dodatnie Lw [m]
ŋ1 = 0,7 ŋ2=0,662 ŋ3 = 0,623 ŋ4 = 0,585 ∑ ŋ= 2,569
pole Lw = 7,644 m2
Rzędne ujemne Lw [m]
ŋ1 = -0,3 ŋ2=-0,262 ŋ3 = -0,223 ŋ4 = -0,185 ∑ ŋ= -0,969
pole Lw = -3,276 m2
Faza I
Tmax = 26,270 *7,644+ 19,716 * -3,276= 136,218 kN
Tmin = 19,716 * 7,644+ 26,270 * -3,276= 64,648 kN
Faza II - obciążenia stałe
Tmax = 10,548 * 7,644+ 7,911 * -3,276= 54,712 kN
Tmin = 7,911 * 7,644+ 10,548 * -3,276= 25,916 kN
Faza II - obciążenia zmienne
Tmax = 6,760 * 7,644+ 68,68 * 2,569= 219,307 kN
Tmin = 6,760 * -3,276+ 68,68 * -0,969= -84,932
Suma
Tmax = 54,712 +219,307 = 274,0195 kN
Tmin = 25,916 + (-84,932) = -59,016 kN
Linia wpływu tnącej w pkt 4
X Є (0; 12,48)
Rzędne dodatnie Lw [m]
ŋ1 = 0,6 ŋ2=0,562 ŋ3 = 0,523 ŋ4 = 0,485 ∑ ŋ= 2,169
pole Lw = 5,616 m2
Rzędne ujemne Lw [m]
ŋ1 = -0,4 ŋ2=-0,362 ŋ3 = -0,323 ŋ4 = -0,285 ∑ ŋ= -1,369
pole Lw = -3,744 m2
Faza I
Tmax = 26,270 *5,616+ 19,716 * -3,744= 73,716 kN
Tmin = 19,716 * 5,616+ 26,270 * -3,744= 12,370 kN
Faza II - obciążenia stałe
Tmax = 10,548 * 5,616+ 7,911 * -3,744= 29,619 kN
Tmin = 7,911 * 5,616+ 10,548 * -3,744= 4,936 kN
Faza II - obciążenia zmienne
Tmax = 6,760 * 5,616+ 68,68 * 2,169= 180,466 kN
Tmin = 6,760 * -3,744+ 68,68 * -1,369= -115,028
Suma
Tmax = 29,619 +180,466 = 210,085 kN
Tmin = 4,936 + (-115,028) = -110,091 kN
Linia wpływu tnącej w pkt 5
X Є (0; 15,6)
Rzędne dodatnie Lw [m]
ŋ1 = 0,5 ŋ2=0,462 ŋ3 = 0,423 ŋ4 = 0,385 ∑ ŋ= 1,769
pole Lw = 3,90 m2
Rzędne ujemne Lw [m]
ŋ1 = -0,5 ŋ2=-0,462 ŋ3 = -0,423 ŋ4 = -0,385 ∑ ŋ= -1,769
pole Lw = -3,90 m2
Faza I
Tmax = 26,270 *3,90+ 19,716 * -3,90= 25,560 kN
Tmin = 19,716 * 3,90+ 26,270 * -3,90= -25,560 kN
Faza II - obciążenia stałe
Tmax = 10,548 * 3,90+ 7,911 * -3,90= 10,284 kN
Tmin = 7,911 * 3,90+ 10,548 * -3,90= -10,284 kN
Faza II - obciążenia zmienne
Tmax = 6,760 * 3,90+ 68,68 * 1,769= 143,374 kN
Tmin = 6,760 * -3,90+ 68,68 * -1,769= -143,374 kN
Suma
Tmax = 10,284 +143,374 = 153,658 kN
Tmin = -10,284 + (-143,374) = -153,658 kN
4. Charakterystyka przekroju stalowego
Wymiary przekroju :
Dźwigar stalowy:
ho= 180m
tw = 20mm
b1=200mm
t1=20mm
b2=600mm
t2=30mm
Całkowita wysokość dźwigara= 1800+20 +30 = 1850mm
Pole przekroju stalowego
Fs = t1 *b1 + t2 * b2 + tw * ho
Fs = 20 * 200 + 30 * 600 + 20 * 1800 = 564cm2
Moment statyczny względem osi x1:
![]()
Środek ciężkości przekroju stalowego:
![]()
![]()
Moment bezwładności przekroju względem osi x przechodzącej przez środek ciężkości dźwigara
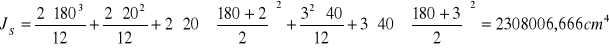
Moment bezwładności przekroju względem środka ciężkości S:
![]()
Wskaźnik bezwładności przekroju:
![]()
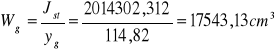
![]()
![]()
Naprężenia w przekroju stalowym w fazie I:
- max moment przęsłowy: M1= 3196,534 kNm
- R=185 MPa
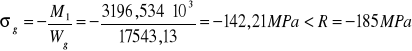
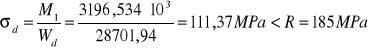
5.Charakterystyka przekroju betonowego
Określenie szerokości współpracującej.
t = 25cm ts = 12,5cm bp= 20cm H=185cm
s= 240cm L= 31,2m d=38cm
b0 = bp + 2ts = 20 + 25 = 45cm
b1=1/2*(s-b0)= 1/2*(240-45)=97,5cm = b2
![]()
![]()
![]()
Szerokość współpracująca płyty na wsporniku λ = 1
bm1= λ * b1 = 1 * 0,975 = 0,975m
W pole wewnętrznym płyty λ = 1
![]()
![]()
![]()
bm2= λ * b2 = 1 * 0,975 = 0,975m
Szerokość współpracująca całkowita:
bm = bo + bm1 + bm2 = 45 + 110 + 68 = 223 cm
Pole przekroju betonowego
![]()
![]()
Moment statyczny względem osi x1
![]()
![]()
Środek ciężkości przekroju względem osi x
![]()
Moment bezwładności względem środka ciężkości
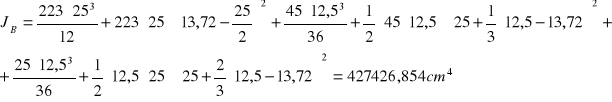
Charakterystyka przekroju zespolonego
Es = 206 GPa Eb=32,6 GPa
![]()
Do obliczeń przyjęto wartość współczynnika α = 15
Pole przekroju zespolonego
![]()
![]()
![]()
![]()
Środek ciężkości przekroju zespolonego
d=38cm g2=3cm h=223cm hs=180cm z0=22,82cm
zb=13,72cm
- odległość pkt. „S” do dolnej półki:
![]()
- odległość między pkt. „B” i „S”
![]()
- odległość między pkt. „S” i „C”
![]()
- odległość między pkt. „B” i „C”
![]()
Warunek na występowanie środka ciężkości przekroju zespolonego w części stalowej:
![]()
oś ciężkości przekroju zespolonego leży w przekroju stalowym
Moment bezwładności względem środka ciężkości dźwigara zespolonego
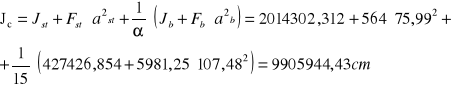
Naprężenia w przekroju stalowym i betonowym w fazie II:
max moment przęsłowy: M2=3861,065 kNm
R=185 MPa
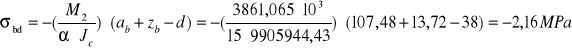
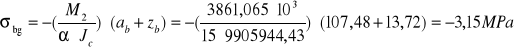
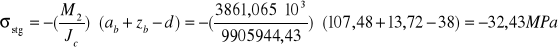
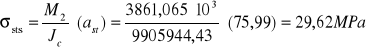
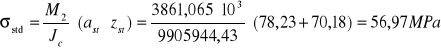
Suma naprężenia w przekroju stalowym fazy I i fazy II
![]()
![]()
Suma naprężeń z fazy I i II mieszczą się w granicach dopuszczalnych
Stopień wykorzystania przekroju:
![]()
29
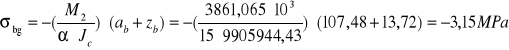
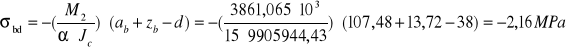
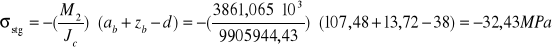
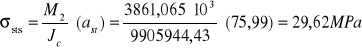
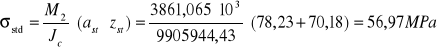
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Projekt mostu sprężonego, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 8, Podstawy konstru
Mathcad Projekt mostu sprężanego
Projekt mostu - tabela momentow Adam poprawka, Budownictwo UTP, III rok, DUL stare roczniki, drogowe
Opis projektowanego mostu, Budownictwo0, Mosty(1)
PROJEKT MOSTU, Opis most
Projekt mostu sprężonego, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 8, Podstawy konstru
Projekt produkcji parówek obliczania maszyny, Procesy Produkcyjne
projekt grubosci szybu , Obliczenie grubości obudowy szybowej
Projekt Rzędzian tabelki i obliczenia
Projekt MJW 2010 (obliczenia)
BUD OG projekt 16 Przykład obliczenia ławy fundamentowej
projekt fundamentu palowego [obliczenia+rysunki], Cwiczenie 2
MiUMIŚ projekt przewodnik do obliczen v5
Budownictwo Ogólne 2 - Projekt - przykład 2, Pozycja obliczeniowa nr 4, Obliczenia ław fundamentowyc
Projekt Nr 3 Wał Obliczenia Stare
Projekt Nr 3 Wał Obliczenia
Projekt Nr 3 Wał Obliczenia
7. stopnie-odporn-stali, Studia, Projekt - materialy konstrukcyjne, 4. Obliczenia, 1. Wytyczne i nor
więcej podobnych podstron