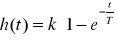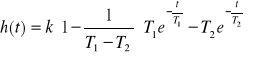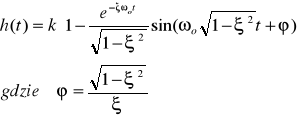Dr inż. Edward Żak

Podstawy automatyki - wykład

„CZŁONY UKŁADÓW REGULACJI AUTOMATYCZNEJ”

Członem będziemy nazywali element układu sterowania, w którym wyodrębniono wielkość wejściową np.
zwaną wymuszeniem i wielkość wyjściową np.
zwaną odpowiedzią, rozpatrywany z punktu widzenia matematycznej funkcji przetwarzania
w
.

Rys.1. Umowne oznaczenie członu

1. Człon proporcjonalny (bezinercyjny, wzmacniający)

Równanie dynamiki:

Transmitancja operatorowa: G(s) = k Parametry: k - współczynnik wzmocnienia

Charakterystyki czasowe:

h(t)=k1(t)

Odpowiedź członu jest proporcjonalna do wymuszenia (stąd nazwa element proporcjonalny).

Odpowiedź członu ma tę samą postać co wymuszenie, odpowiedź „nadąża” za wymuszeniem - nie występuje inercja (stąd nazwa element bezinercyjny).

Transmitancja widmowa:
P(ω) = k, Q(ω) =0

Charakterystyki częstotliwościowe:

Charakterystyka amplitudowo - fazowa członu proporcjonalnego (bezinercyjnego) dla pulsacji zmieniającej się od ω = 0 do ω=∞ ma postać punktu o współrzędnych (k, j0). Logarytmiczne charakterystyki (amplitudowa i fazowa) członu są liniami prostymi.

2. Człon inercyjny pierwszego rzędu

Równanie dynamiki:

Transmitancja operatorowa:
Parametry: k - wsp. wzmocnienia, T - stała czasowa

Charakterystyki czasowe:

Z zależności Y(s) = G(s)X(s) oraz X(s) = L{1(t)} = 1/s

Równanie M(s) = 0 ma tylko jeden pierwiastek niezerowy
, stąd dla n=1 z zależności

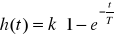
1(t)

Im mniejsza jest stała czasowa T, tym przebieg charakterystyki skokowej h(t) członu inercyjnego pierwszego rzędu zbliża się coraz bardziej do przebiegu charakterystyki skokowej h(t) = kl(t) członu bezinercyjnego. W szczególnym przypadku dla stałej czasowej równej zeru z członu inercyjnego pierwszego rzędu otrzymujemy człon bezinercyjny.

Transmitancja widmowa:

;

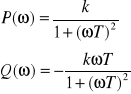
Charakterystyki częstotliwościowe:

Charakterystyka amplitudowo-fazowa członu inercyjnego pierwszego rzędu dla pulsacji zmieniającej się od ω= 0 do ω=∞ ma postać półokręgu o średnicy k ze środkiem w punkcie (k/2, j0). W zależności od wartości stałej czasowej T zmienia się tylko rozkład punktów odpowiadających poszczególnym pulsacjom ω₁, ω₂, ω₃, ω₄.

Logarytmując moduł transmitancji widmowej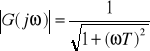

otrzymuje się logarytmiczną charakterystykę amplitudową

Charakterystyki amplitudowo-fazowa członu inercyjnego pierwszego rzędu dla dwóch różnych stałych czasowych T₁ i T₂ (T₂>T₁): a)stała czasowa T₁, b) stała czasowa T₂

Wykreślając logarytmiczną charakterystykę amplitudową wygodnie jest przyjąć jej aproksymację liniami prostymi (charakterystyki asymptotyczne - Bodego)

3. Człon inercyjny drugiego rzędu i człon inercyjny n-tego rzędu

Równanie dynamiki:

Transmitancja operatorowa:

Parametry: k - współczynnik wzmocnienia członu, T₁,T₂ - stałe czasowe

Człon inercyjny drugiego rzędu o transmitancji G(s) otrzymać możemy w wyniku połączenia łańcuchowego (kaskadowego) dwóch nie obciążających się wzajemnie członów inercyjnych pierwszego rzędu o transmitancjach

Charakterystyki czasowe:

Równanie M(s)=0 ma dwa pierwiastki rzeczywiste

Biorąc pod uwagę, że

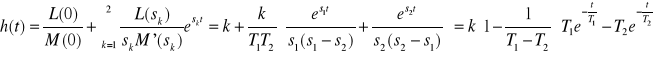
Transmitancja widmowa:

Charakterystyki częstotliwościowe:

Charakterystyka amplitudowo - fazowa członu inercyjnego drugiego rzędu dla pulsacji zmieniającej się od ω=0 do ω=∞ jest regularna i przechodzi przez dwie ćwiartki.

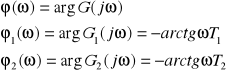
Logarytmiczna charakterystyka amplitudowa i fazowa członu inercyjnego drugiego rzędu jest sumą logarytmicznych charakterystyk amplitudowych i odpowiednio fazowych dwóch członów inercyjnych pierwszego rzędu.

Członem inercyjnym n - tego rzędu nazywamy człon o transmitancji operatorowej

Parametry: k - współczynnik wzmocnienia członu, T₁,T₂,...,T_n stałe czasowe

Człon taki otrzymuje się w wyniku połączenia łańcuchowego „n” nieobciążających się wzajemnie członów inercyjnych pierwszego rzędu o transmitancjach:

Charakterystyki czasowe:

Charakterystyka amplitudowo-fazowa:

4. Idealny człon różniczkujący

Równanie dynamiki:

Transmitancja operatorowa:

Charakterystyki czasowe:

Odpowiedź idealnego członu różniczkującego dla x(o) =0 jest proporcjonalna do pierwszej pochodnej względem czasu wymuszenia.

h(t) = k δ(t) bo transformata funkcji Dirac'a δ(t) jest równa jedności

h(t) = k δ(t)

Transmitancja widmowa:

Charakterystyki częstotliwościowe:

Charakterystyka amplitudowo—fazowa idealnego członu różniczkującego dla pulsacji zmieniającej się od ω = 0 do ω = ∞ pokrywa się z dodatnią półosią liczb urojonych

Logarytmiczne charakterystyki amplitudowa i fazowa ideal­nego członu różniczkującego mają postać

5. Rzeczywisty człon różniczkujący (z inercją)

Równanie dynamiki:

Transmitancja operatorowa:

Parametry: k - współczynnik wzmocnienia członu, T - stała czasowa.

Charakterystyki czasowe:

Biorąc pod uwagę, że
otrzymamy

Transmitancja widmowa:

Charakterystyka amplitudowo - fazowa rzeczywistego członu różniczkującego dla pulsacji zmieniającej się od ω=0 do ω=∞ma postać półokręgu o średnicy k/T i środku w punkcie (k/2T,j0).

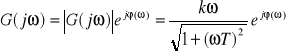
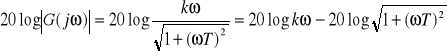
6. Idealny człon całkujący

Równanie dynamiki:

Transmitancja operatorowa:
Parametry: k - współczynnik wzmocnienia członu, tzw. prędkościowy.

Charakterystyki czasowe:

Dla transformaty H(s) charakterystyki skokowej h(t) idealnego członu całkującego z zależności Y(s) =G(s)X(s) oraz dla X(s) = 1/s otrzymamy
. Biorąc pod uwagę, że
h(t)=kt

Transmitancja widmowa:

przy czym

Charakterystyka amplitudowo - fazowa idealnego członu całkującego dla pulsacji zmieniającej się od ω=0 do ω=∞ pokrywa się z ujemną półosią liczb urojonych.

Logarytmiczne charakterystyki amplitudowa i fazowa

7. Rzeczywisty człon całkujący

Równanie dynamiki:

Transmitancja operatorowa:
Parametry: k - współczynnik wzmocnienia członu, T - stała czasowa.

Charakterystyki czasowe:

Biorąc pod uwagę, że

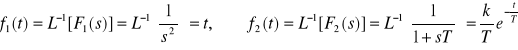
oraz korzystając z twierdzenia o splocie otrzymamy

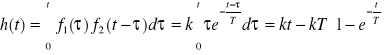
Transmitancja widmowa:

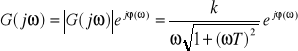
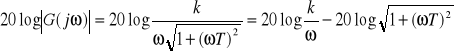
8. Człon oscylacyjny drugiego rzędu

Równanie dynamiki:

Transmitancja operatorowa:

lub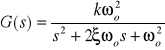

Parametry: k - współczynnik wzmocnienia , ω_o- pulsacja oscylacji własnych ,

ξ - względny współczynnik tłumienia, T - stała czasowa

Charakterystyki czasowe:

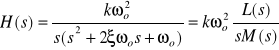
Równanie M(s)=0 ma dwa pierwiastki zespolone sprzężone

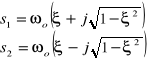
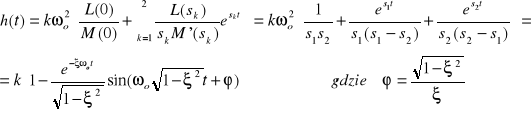
Transmitancja widmowa:

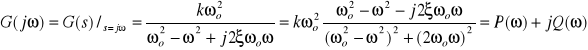
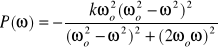
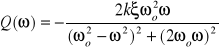
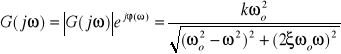
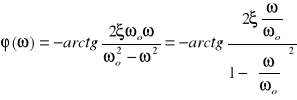
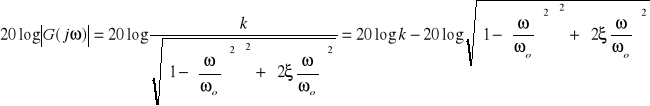
Logarytmiczna charakterystyka amplitudowa dla
osiąga maksimum dla ω=ω_o, przy czym wartość tego maksimum jest tym większa im mniejszą wartość ma względny współczynnik tłumienia ξ.. Dla ξ=0 oraz ω=ω_o logarytmiczna charakterystyka amplitudowa osiąga wartość nieskończenie wielką.

9. Człon opóźniający (opóźnienie transportowe, czyste opóźnienie) Równanie dynamiki: Transmitancja operatorowa: Parametry: - czas opóźnienia Charakterystyki czasowe: (z twierdzenia o przesunięciu) Transmitancja widmowa: P(ω) = cos ωT, Q(ω) = - sin ωT Charakterystyka amplitudowo - fazowa członu opóźniającego ma postać okręgu o promieniu równym jedności i środku w początku układu współrzędnych . Logarytmiczna charakterystyka amplitudowa członu opóźniającego pokrywa się z osią odciętych, logarytmiczna charakterystyka fazowa jest linią prostą przechodzącą przez początek układu.

Podstawowe człony dynamiczne

--------------------------------------------------------------------------------------------------------------------------------------

12

1

Podstawowe człony dynamiczne

G(s)

---