1

Dr Galina

Cariowa

2

Legenda

Iteracyjne układy
kombinacyjne

Sumatory
binarne

Sumatory - substraktory
binarne

Funkcje i układy
arytmetyczne

Układy
mnożące

3

Układy arytmetyczne

Układ arytmetyczny jest to kombinacyjny układ
logiczny, który wykonuje operacje arytmetyczne:

dodawanie;

odejmowanie;

mnożenie;

dzielenie

liczb binarnych lub liczb dziesiętnych przedstawionych
za pomocą kodu binarnego.

Podstawowe bloki arytmetyczne :

półsumator

(ang.

half

adder

)

pełny sumator

(ang.

full adder

),

Z tych bloków projektowane inne układy arytmetyczne.

4

Układy iteracyjne

Jeśli w rozwiązywanym zadaniu nie jest określona
liczba zmiennych, wtedy można zaprojektować układ
dla jednej lub kilku zmiennych, a następnie łączyć
takie układy ze sobą.

Takie układy przyjęto nazywać

układami

iteracyjnymi.

Zaleta układów iteracyjnych

: możliwość ich

łatwego rozbudowywania dla większej liczby
zmiennych.

Wady układów iteracyjnych

:

- nie stanowią one minimalnego

rozwiązania

pod względem liczby

bramek;

- wnoszą znacznie większe opóźnienie
niż

klasycznie projektowane układy.

5

Sieć iteracyjna

Układy iteracyjne

są zbudowane z sieci komórek

kombinacyjnych.

Podstawowe bloki funkcjonalne realizujące proste
funkcje składowe są określane jako

komórki,

A całą implementację określamy jako

sieć

komórek

.

Komórki w sieci są często
identyczne

Cały blok
funkcjonalny
jest określany
jako

sieć

iteracyjna

.

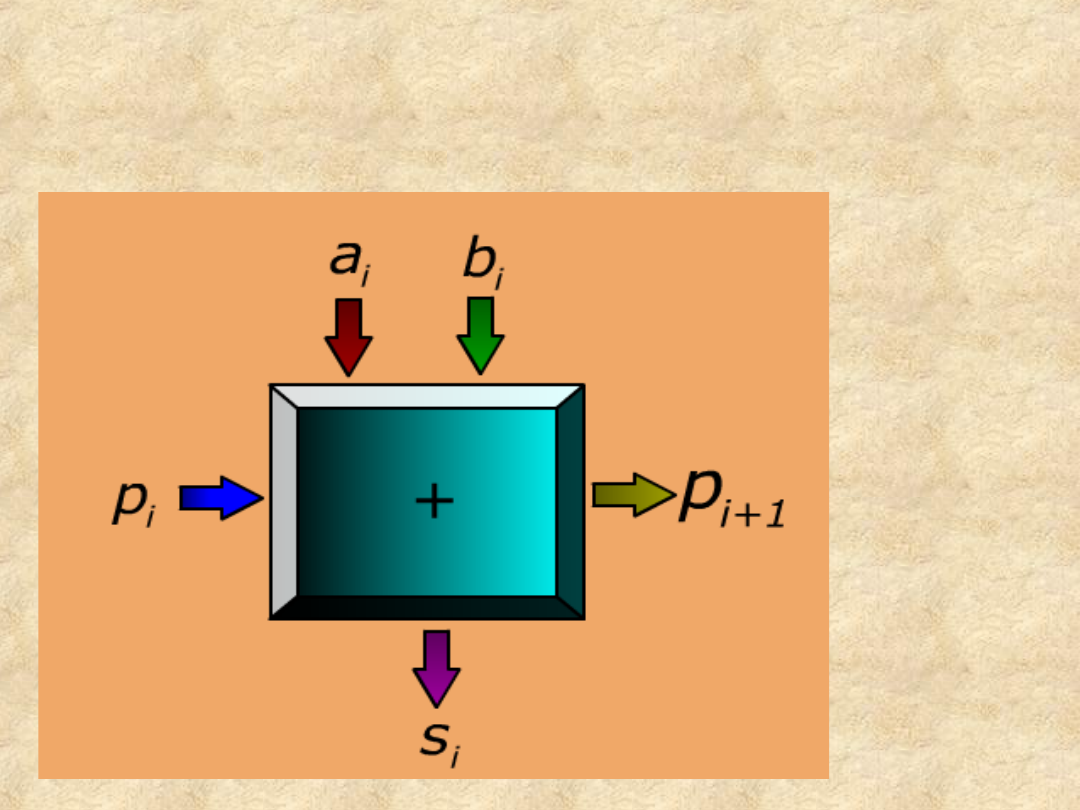
6

Symbol i-tej komórki dwóch

liczb

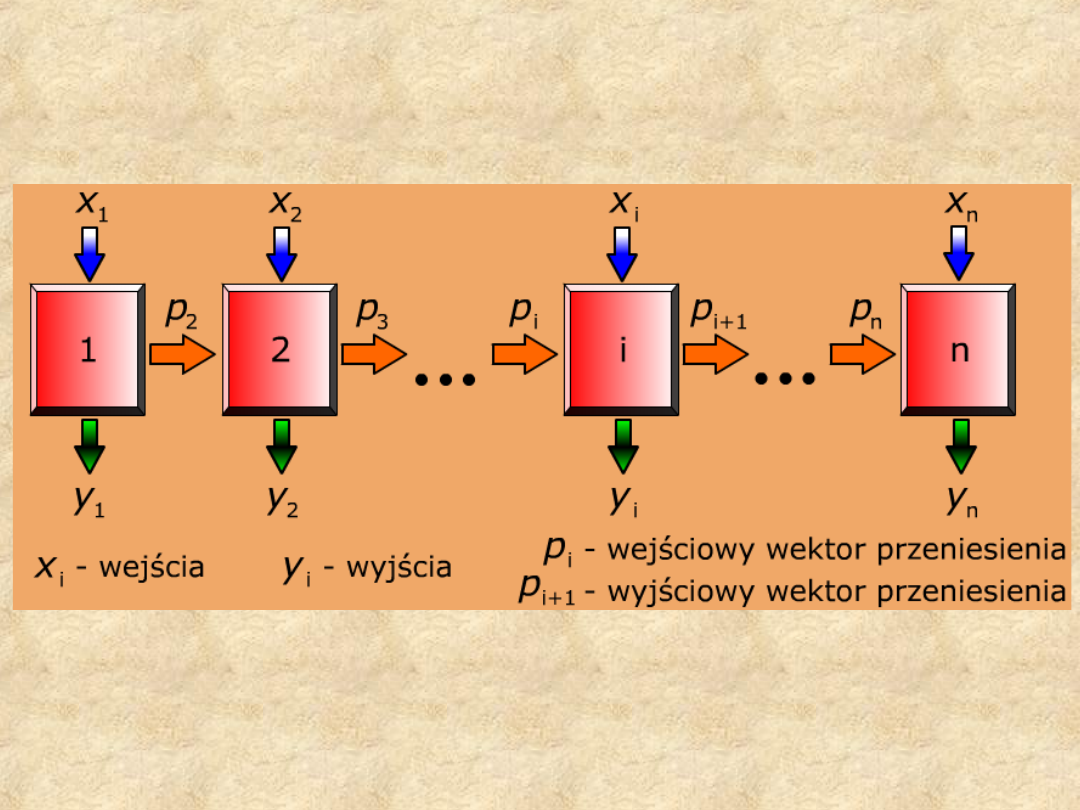
7

Schemat blokowy układu

iteracyjnego

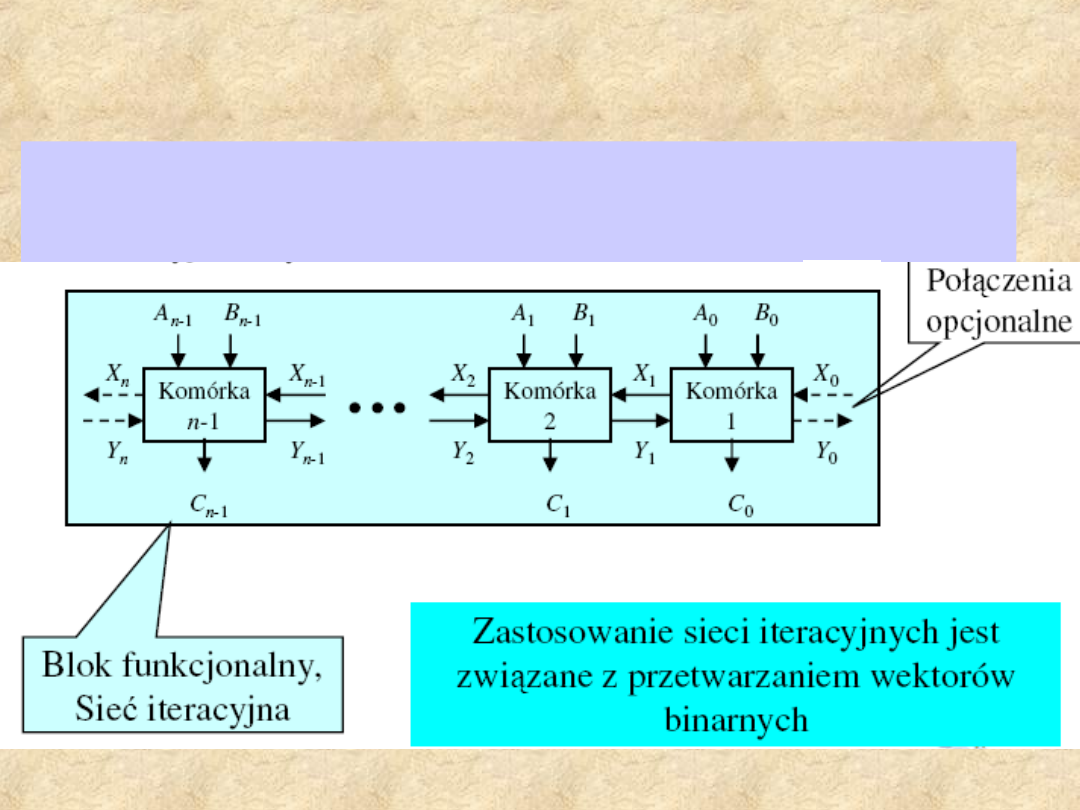
8

Schemat blokowy układu

iteracyjnego

Układ wykonujący działania na dwóch wektorach n
-bitowych wejściowych A,B i tworzy n -bitowy wektor
wyjściowy C.

9

Układ iteracyjny

Między każdą parą komórek
sieci istnieją dwa boczne
połączenia.

Liniami przerywanymi
zaznaczone opcjonalne
połączenia na prawym i
lewym krańcu sieci komórek.

Liczba zastosowanych
połączeń i ich funkcji
wpływa zarówno na koszt,
jak i na szybkość układu
iteracyjnego.

Zdefiniujemy komórki
wykonujące dodawanie
bitów na pojedynczej
pozycji, a następnie
zdefiniujemy układ
realizujący dodawanie
dwóch liczb binarnych.

10

Układ realizujązujący

dodawanie dwóch liczb

binarnych

Dodawanie składa się z czterech możliwych operacji elementarnych:

0+0=0, 0+1=1, 1+0=1, 1+1=10

Wynik dodawania jest zawsze
reprezentowany dwoma bitami,

bitem

przeniesienia

i sumy.

Przeniesienie jest dodawane do
następnej pary bardziej znaczących
bitów.

Układ kombinacyjny realizujący dodawanie
dwóch bitów jest nazywany

półsumatorem

.

Sumator realizujący sumę trzech bitów (dwóch
bitów znaczących i bitu przeniesienia z
poprzedniej pozycji) jest nazywany

pełnym

sumatorem.

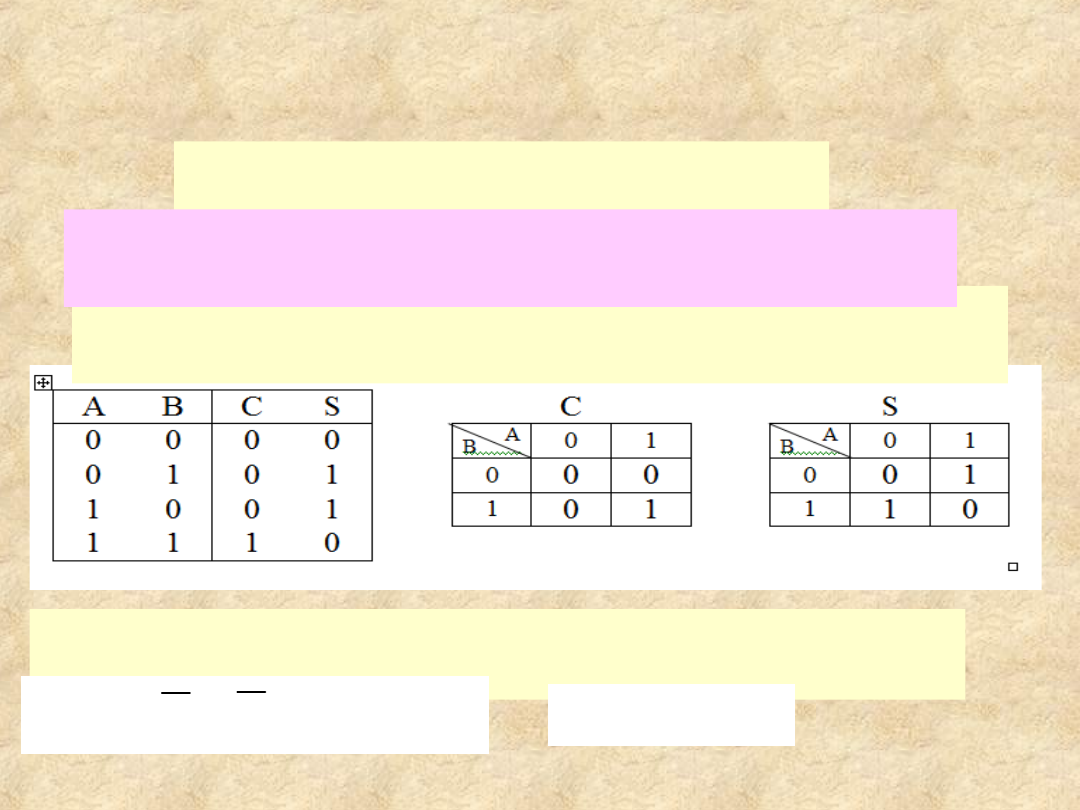
11

Półsumator

(dodawanie jednobitowych liczb

dwójkowych)

Tablica prawdy półsumatora i 2 tablicy
Karnaugha

Wejście – bity dodajnej A i
dodajnika B.

Wyjście – bity sumy S i przeniesienia C (ang.
carry)

Z tablicy prawdy można odczytać funkcję boolowskie dla
obu wyjść

.

B

A

B

A

B

A

S













B

A

C





12

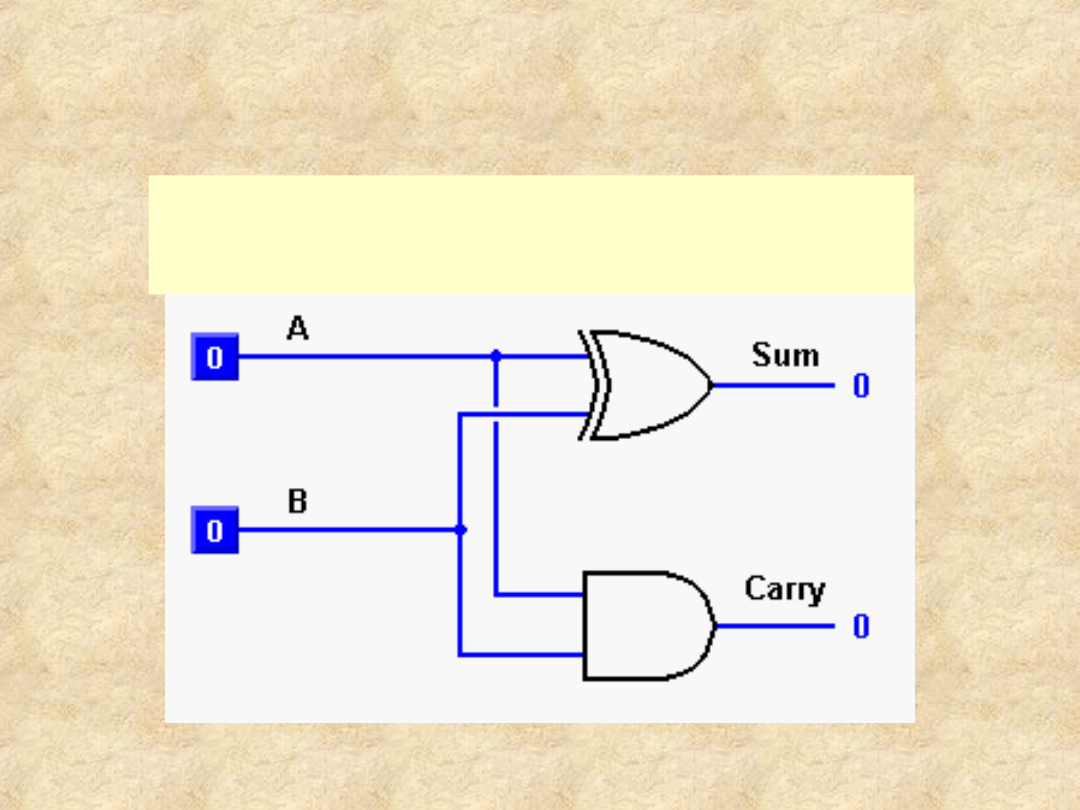
Schemat logiczny

półsumatora

Półsumator można zrealizować na

jednej bramce

EXOR

i

jednej bramce AND

13

Pełny sumator -

Przy dodawaniu bitów oprócz bitów wejściowych
trzeba uwzględniać przeniesienie z mniej
znaczącej pozycji.

Funkcje boolowskie sumatora jednopozycyjnego są

funkcjami trzech zmiennych

: wartości danych

X

i

Y

oraz przeniesienia z mniej znaczącej

pozycji

Z

.

Operacja jednobitowego dodawania (dodawania dwóch bitów
wraz z przeniesieniami) polega na obliczaniu wartości dwóch
funkcji:

S

–jest binarnym wynikiem

dodawania trzech

bitów X,Y i Z;

C

–jest wartością przeniesienia

(wyjściowego)

na następną pozycję.

generuje sumę trzech bitów
wejściowych.

14

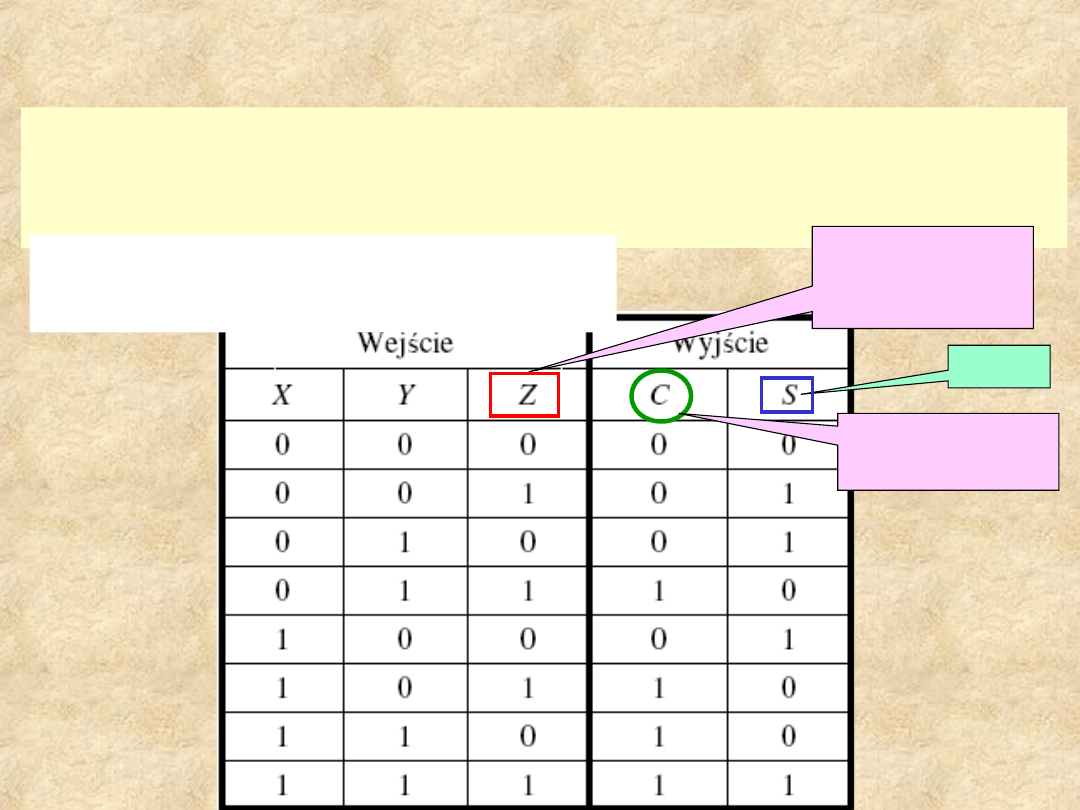
Pełny sumator

Układ generuje sumę trzech bitów wejściowych (dwóch
bitów znaczących i bitu przeniesienia z poprzedniej
pozycji)

suma

Tablica prawdy dla funkcji
C i S:

Przeniesienie

wyjściowe

Przeniesienie

z poprzedniej

pozycji

15

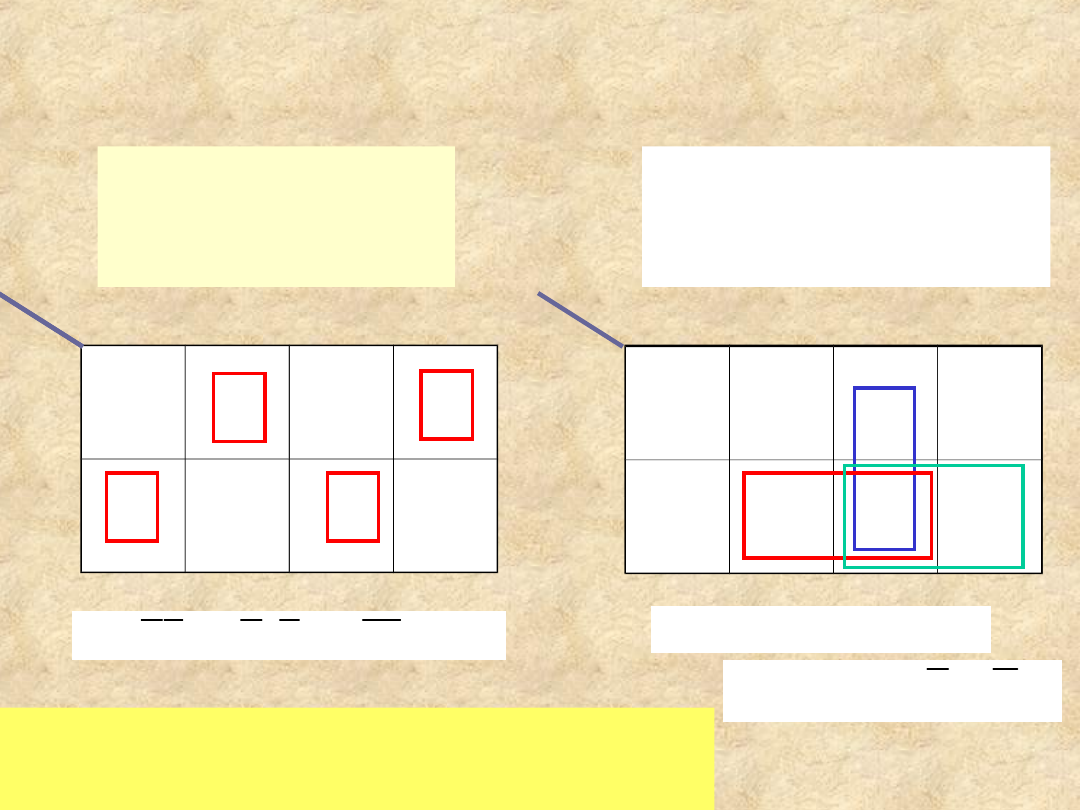
Pełny sumator

Tablica
Karnaugcha dla
wyjścia sumy

x

yz

00

01

11

10

0

1

1

1

1

1

00

01

11

10

0

1

x

yz

1

1

1

1

Tablica Karnaugha
dla wyjścia

przeniesienia

XYZ

Z

Y

X

Z

Y

X

Z

Y

X

S

















YZ

XZ

XY

C

)

(

Y

X

Y

X

Z

XY







Dwupoziomowa

implementacja

wymaga siedmiu bramek AND i
dwóch bramek OR.

16

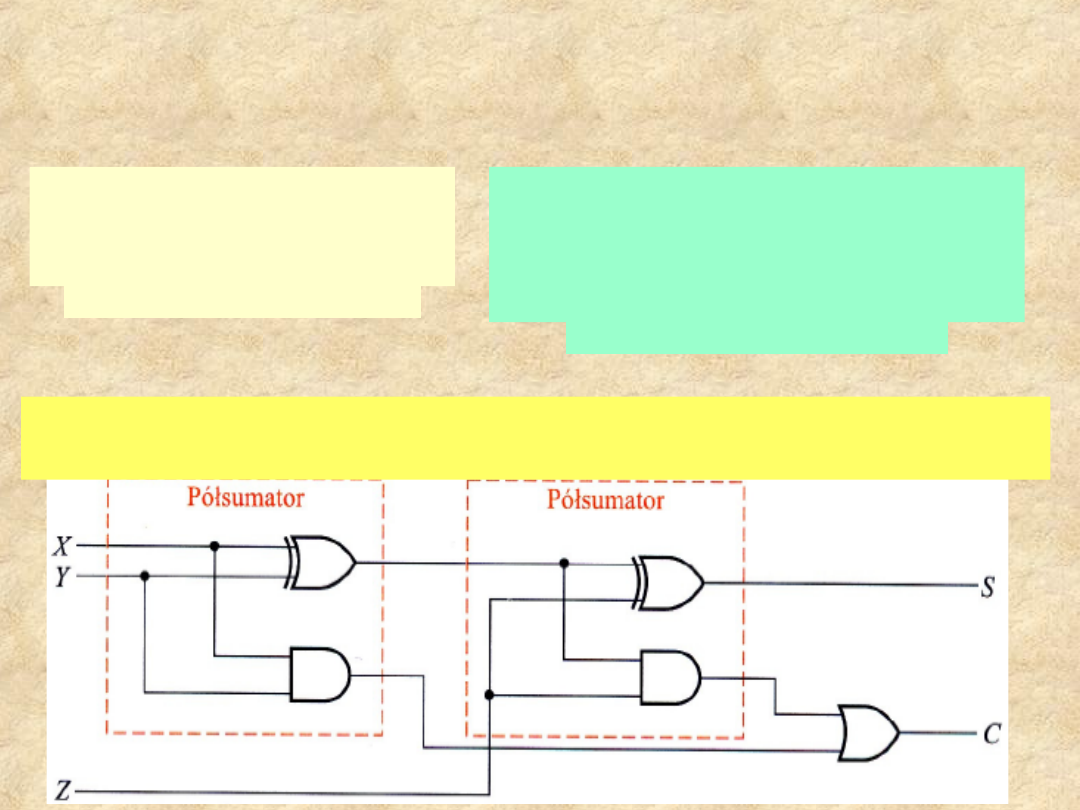
Pełny sumator

Z

Y

X

S







)

(

Y

X

Z

XY

C







Funkcja wyjścia S jest
funkcją kontroli
nieparzystości :

Funkcja wyjścia C może być tak
przekształcona, by zawierała
operację EXOR na zmiennych X i
Y:

Schemat logiczny

wielopoziomowej

implementacji pełnego

sumatora.

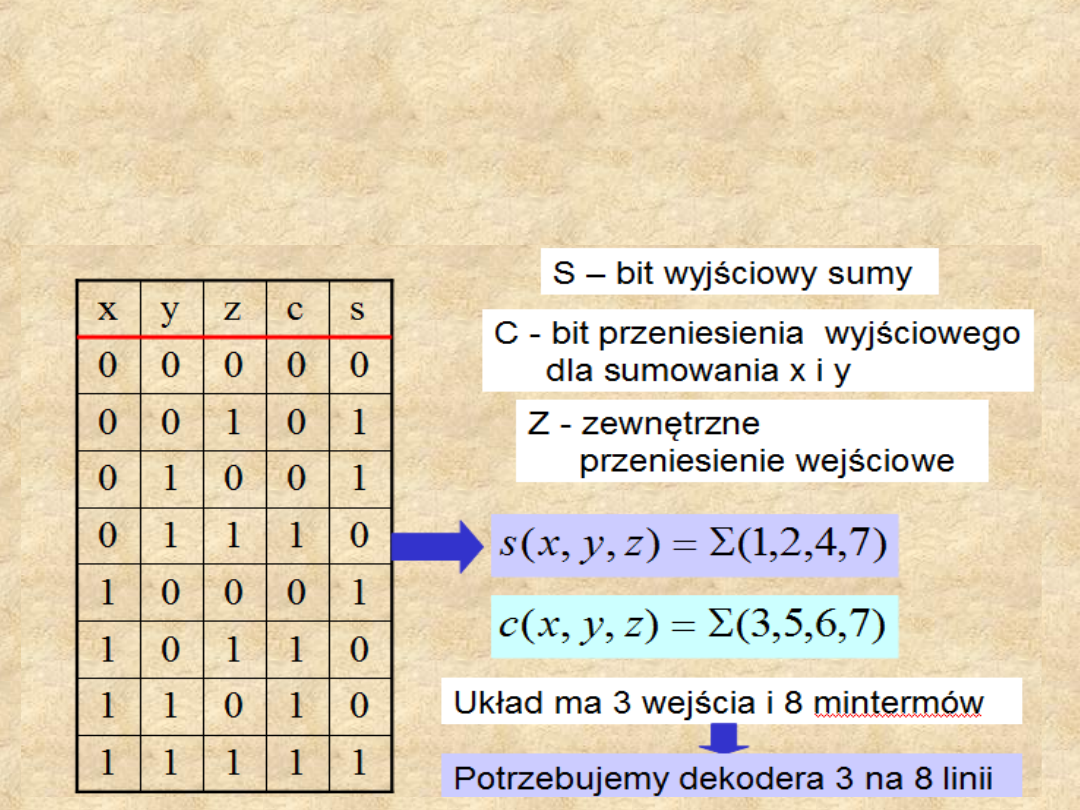
17

Implementacja 1 –bitowego

sumatora

na dekoderze i bramce

OR

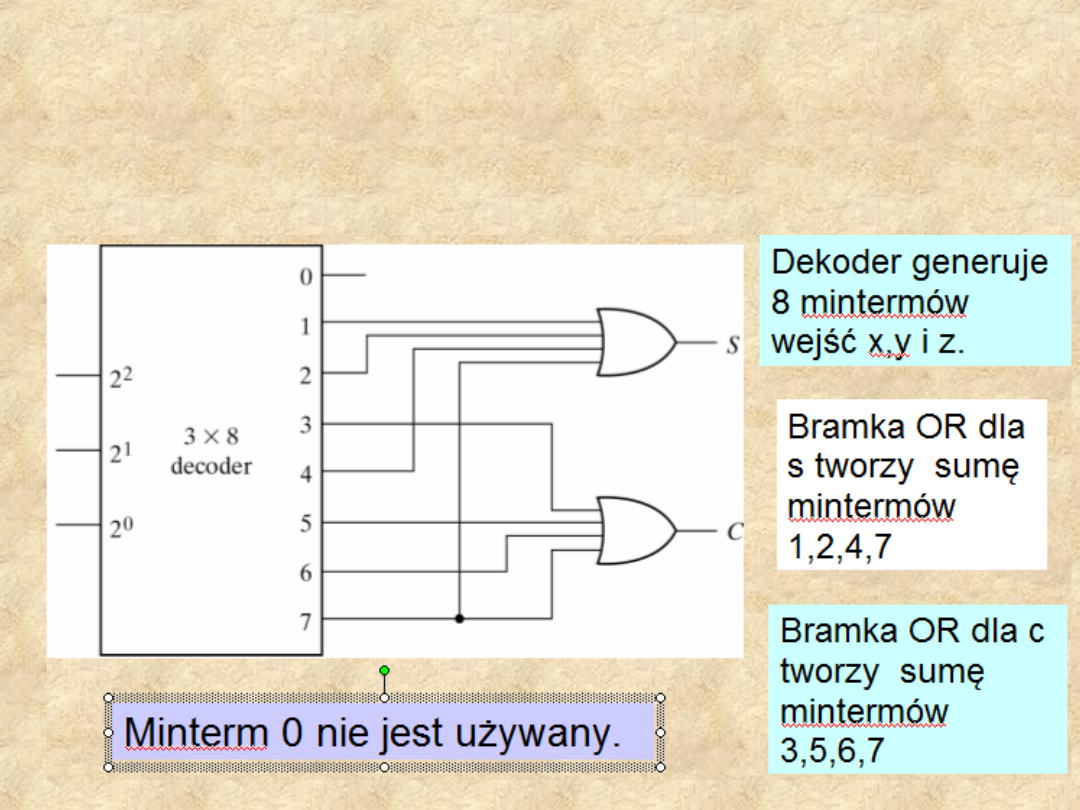
18

Implementacja 1 –

bitowego sumatora

na

dekoderze i bramce OR

19

Przykład. Sumator dwóch

czterobitowych liczb

binarnych.

Projektowanie zwykłego układu
kombinacyjnego realizującego podaną
funkcję polega na utworzeniu tablicy
Karnaugha dla

ośmiu zmiennych

wejściowych i 4 zmiennych
wyjściowych.

Już dla niewielkiej liczby sumowanych
bitów tablica Karnaugha jest bardzo
rozbudowana.

20

Sumator dwóch

czterobitowych liczb

binarnych

W celu uzyskania

sumatora dla słów

czterobitowych

wystarczy:

połączyć 4 bloki wyznaczone powyżej,

odpowiednio upraszczając blok

pierwszy

(przeniesienie =0) i ostatni

blok (brak

przeniesienia).

21

Sumator kaskadowy

Równoległy sumator

jest układem,

który tworzy sumę dwóch liczb binarnych
tylko za pomocą kombinacyjnego układu
logicznego .

Sumator równoległy zawiera

n

pełnych

sumatorów, połączonych

równoległe

,

a by wygenerować sumę

wszystkie bity

wejściowe są podawane równocześnie.

Pełne sumatory połączone w
kaskadzie,

a wyjście przeniesienia jednego
pełnego sumatora jest podawane na
wejście przeniesienia następnego
pełnego sumatora.

Sumator
równoległy
jest określany
jako

sumator

kaskadowy

.

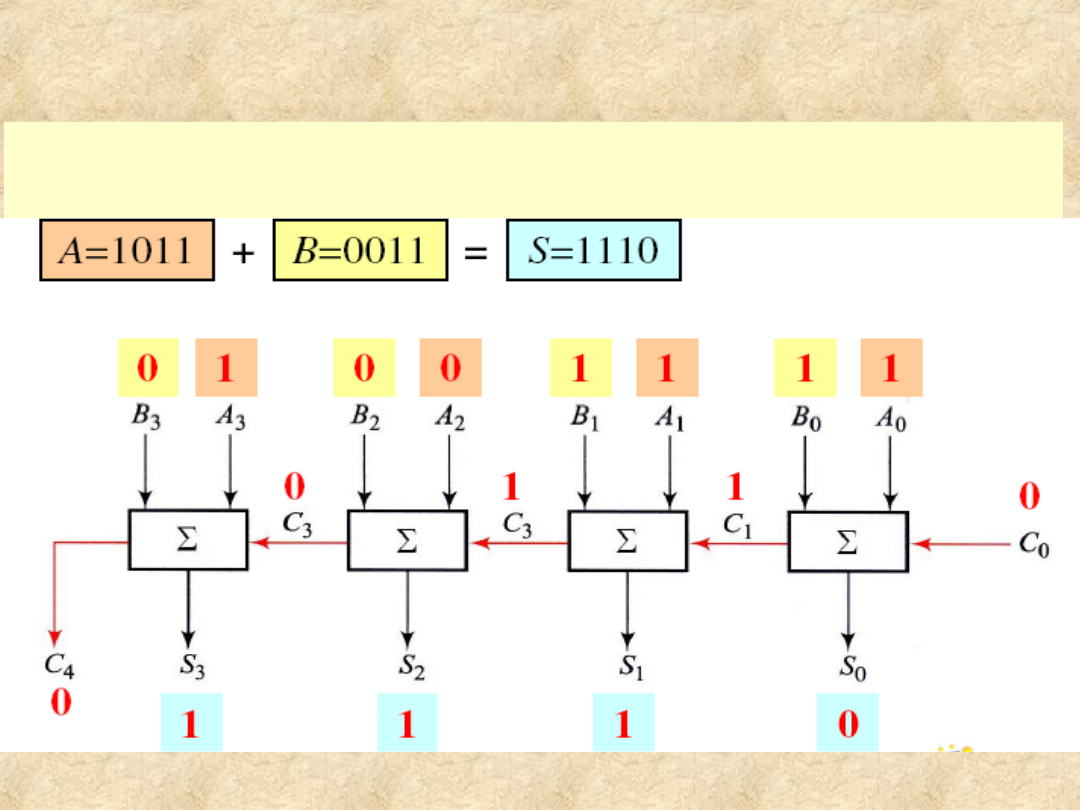
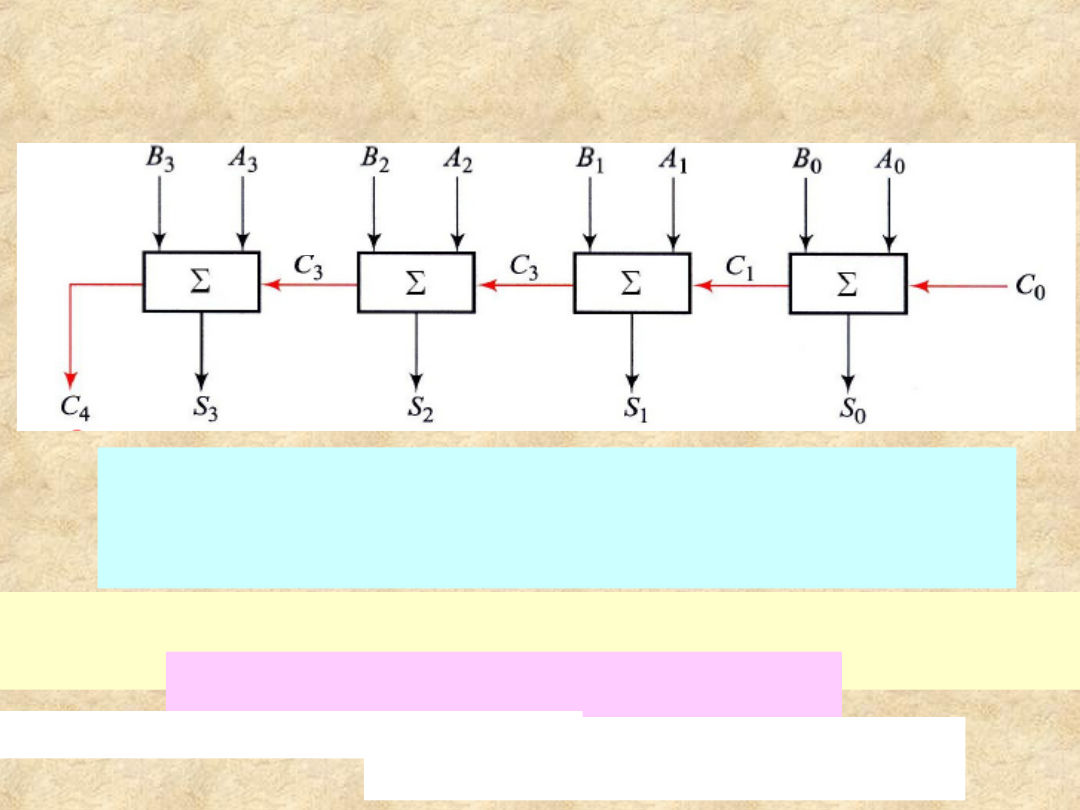
22

4-bitowy sumator

kaskadowy

tworzy cztery bloki pełnych

sumatorów połączonych

ze sobą:



23

4-bitowy sumator

kaskadowy

Układ ma

9 wejść

(wejścia

dwóch 4-

bitowych liczb i wejście
przeniesienia C

0

).

kwadratów w

tablicy prawdy przy
projektowaniu

klasyczną

metodą

512

2

9



4 sumatory
połączonych
kaskadowo

Nieskomplikowa
na
implementacja

Wielokrotne
wykorzystywanie
identycznych elementów

Wykorzystanie układów
iteracyjnych

Wejście
przeniesienia C

0

i

wyjście C

4

służą dla

dalszej rozbudowy.

24

Sumator kaskadowy

Długi czas
opóźnienia

Duża liczba bramek na
ścieżce propagującej
przeniesienia

Najdłuższa ścieżka przez n- bitowy
sumator ma opóźnienie równe opóźnieniu
2n+2 bramek.

Alternatywne rozwiązanie-

sumator z

przeniesieniami jednoczesnymi

(ang.carry

look-ahead adder).

25

Sumator z

przeniesieniami

jednoczesnymi

(antycypowanymi)

Znacznie mniejsze
opóźnienie

Bardziej skomplikowana struktura
sprzętowa

Sumator kaskadowy

Sumator z przeniesieniami
jednoczesnymi

Przekształcenie części układu
realizującej propagację przeniesień
do dwupoziomowego układu
logicznego

(praca
własna)

26

Układ wykonujący

odejmowanie A-B

Układ składa się z sumatora równoległego i
inwerterów umieszczonych między każdym
zaciskiem B a odpowiednim wejściem sumatora.

1

Wykonywana operacja

: A plus uzupełnienie do 1 liczby B

plus 1. To odpowiada A plus uzupełnienie

do 2.

Uzyskamy A-B, gdy

B

A

lub uzupełnienie do 2 różnicy B-A, gdy
A<B

Substraktor- specjalny układ odejmujący

27

Sumator- substraktor

Operacje dodawania i
odejmowania mogą być
połączone w jednym wspólnym
sumatorze binarnym.

Dla tego celu wprowadza się
bramki EXOR dla każdego pełnego
sumatora.

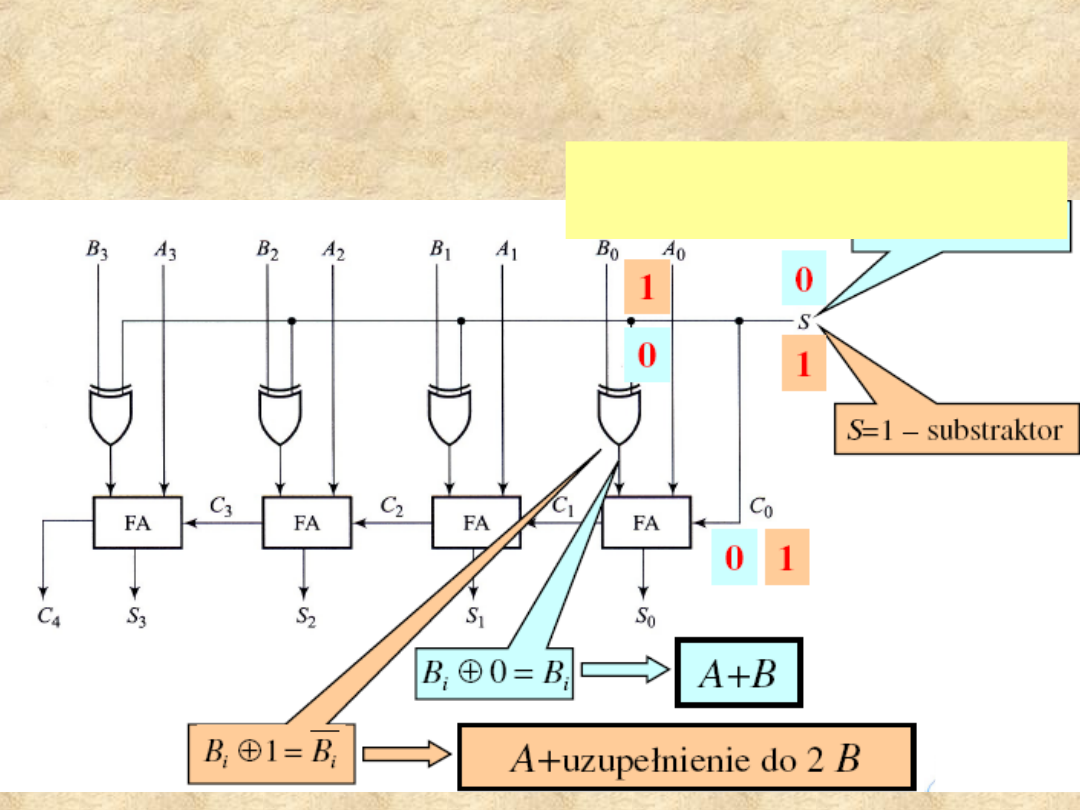
28

4-bitowy sumator-

substraktor

Wejście S steruje
operacjami:

29

4-bitowy sumator-

substraktor

Gdy S=0, mamy
.

Oraz C

0

=0

0



i

B

Układ realizuje
dodawanie

A+B

Gdy S=1, mamy
.

i

i

B

B



1

Gdy S=1, mamy

oraz C

0

=1

i

i

B

B



1

Układ wykonuje
operacje A plus
uzupełnienie do 2 B

Wejście

S

steruje

operacjami.

Na wejścia każdej bramki EXOR są
podawane:

sygnał S i jeden z sygnałów B,Bi.

30

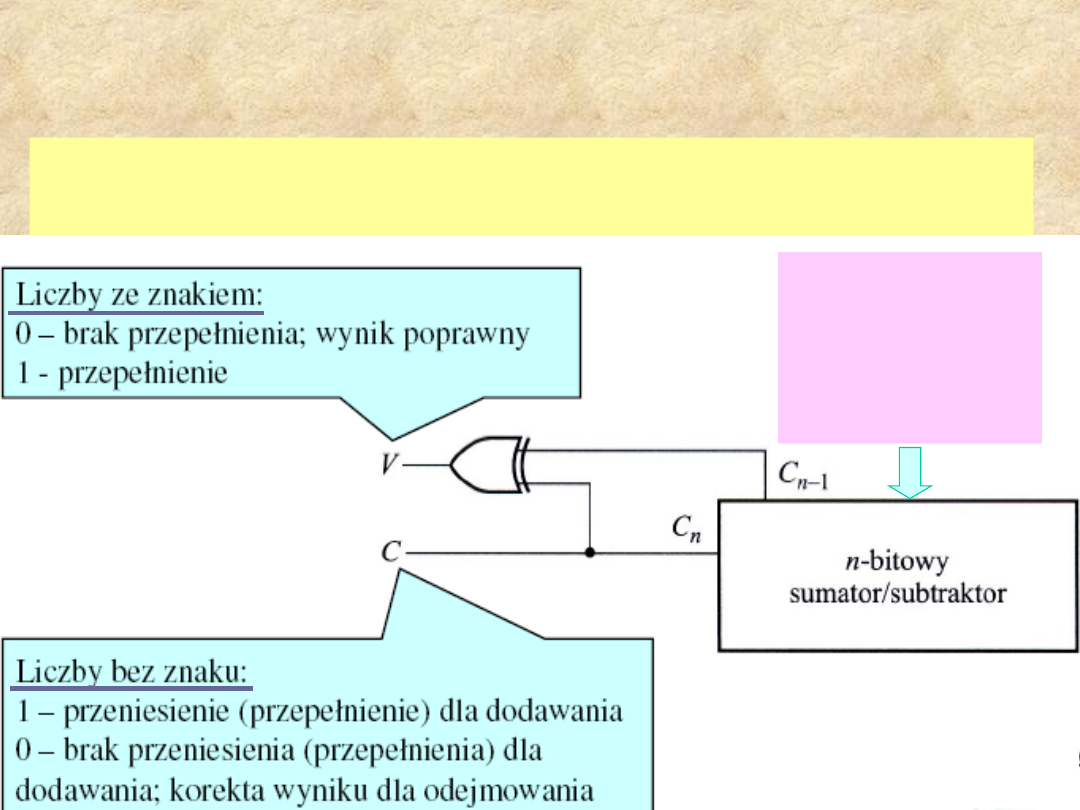
Wykrywanie przepełnienia

Przepełnienie (nadmiar) – sytuacja, gdy wynik
dodawania lub odejmowania dwóch n- bitowych liczb
zajmuje n+1 bitów.

Logiczny układ
do wykrywania
przepełnienia w
dodawaniu i
odejmowaniu.

31

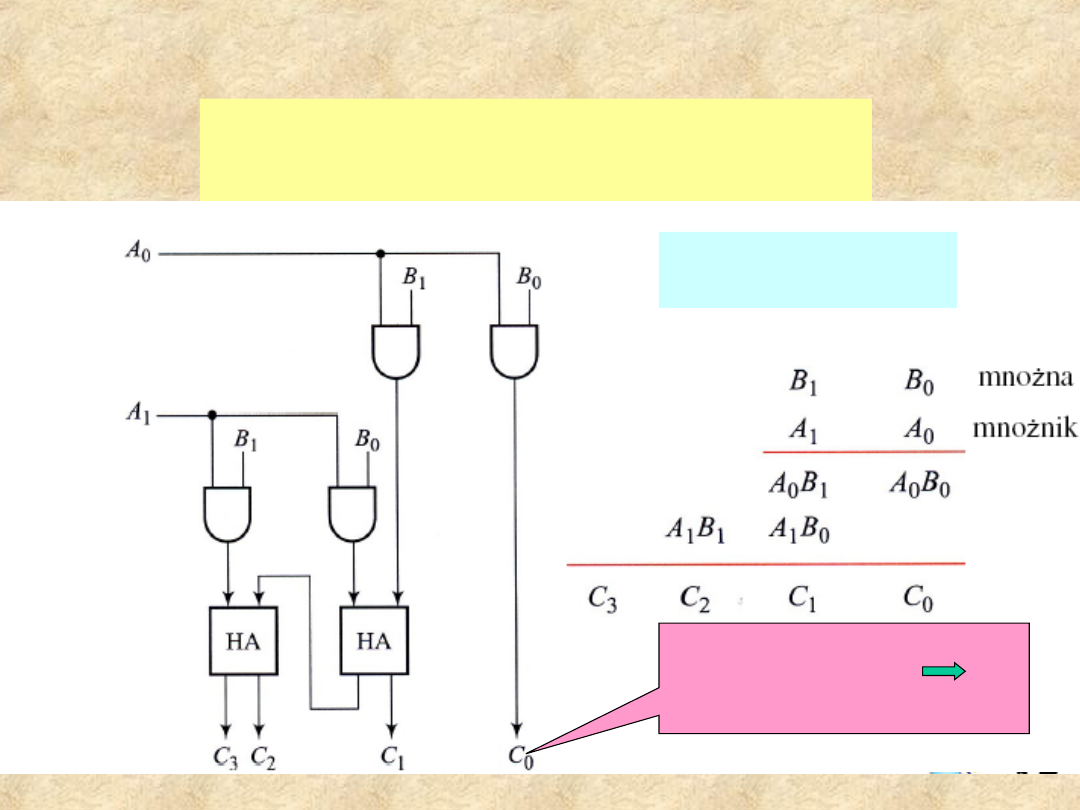
Układ mnożący

Iloczyny częściowe są zrealizowane za pomocą
bramek AND, sumowane w dwóch
półsumatorach HA.

Mnożenie dwóch
liczb dwubitowych:

iloczyn

Najmłodszy bit iloczynu
powstaje na wyjściu bramki
AND nie przechodzi przez
sumator

32

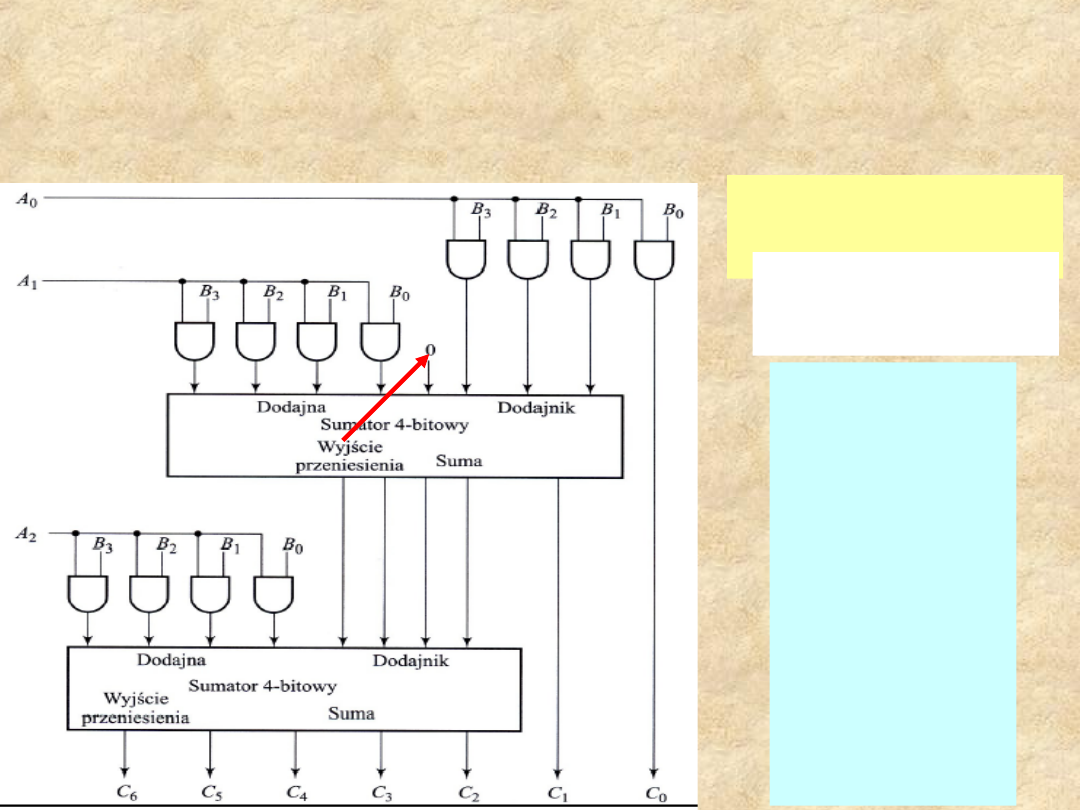
Układ mnożący liczbę 4-

bitową przez 3 - bitową

B

3

B

2

B

1

B

0

-

mnożna

A

2

A

1

A

0

-

mnożnik

Aby
utworzyć 7-
bitowy
iloczyn
potrzebne
są 12
bramek
AND i dwa
4 –bitowe
sumatory.

33

Inne funkcje

arytmetyczne



inkrementowan

ie



dekrementowan

ie



mnożenie przez stałą

wartość



dzielenie przez stałą

wartość



porównywanie z

wykrywaniem liczby
mniejszej i większej

34

DZIĘKUĘ

ZA UWAGĘ