ĆWICZENIA 5 - Finanse przedsiębiorstwa

1.DECYZJE INWESTYCYJNE

Decyzje inwestycyjne przedsiębiorstwa są rozumiane jako decyzje o wykorzystaniu pozyskanego kapitału. Inwestowanie natomiast jest działalnością gospodarczą o odroczonych efektach, mającą na celu poprawę efektywności działania, wzmocnienie pozycji rynkowej, poprawę wyników finansowych w krótkim i długim okresie. Inwestycje wymagają wcześniejszego poniesienia wydatków, aby w późniejszym okresie uzyskać wpływy pieniężne.

Proces podjęcia decyzji inwestycyjnej wymaga analizy ekonomiczno-finansowej składającej się z następujących działań:

1. Określenie potrzeb inwestycyjnych przedsiębiorstwa, czyli obszarów firmy, które należy zmodernizować lub unowocześnić,

2. Określenie wymaganego nakładu inwestycyjnego,

3. Oszacowanie przyszłych oczekiwanych korzyści z przedsięwzięcia inwestycyjnego, opracowanych w oparciu o rachunek przepływów pieniężnych przygotowany według podejścia FCFF (przepływy dla wszystkich stron finansujących planowaną inwestycję tzn. dla właściciela oraz wierzycieli) albo FCFE (przepływy pieniężne dla właściciela),

4. Ustalenie źródeł finansowania inwestycji, obliczenie optymalnej struktury finansowania i obliczanie kosztu kapitału, czyli oczekiwanej przez dostawców kapitału stopy zwrotu z finansowanego projektu,

5. Ocenę możliwości akceptacji projektu inwestycyjnego poprzez wyliczenie mierników finansowych, opierających się na zasadzie porównywania wartości przyszłych korzyści możliwych do osiągnięcia z danej inwestycji z nakładem kapitałowym na tą inwestycję.

1. PRZEPŁYWY PIENIĘŻNE PRZEDSIĘWZIĘCIA INWESTYCYJNEGO

Przygotowane na potrzeby rachunku opłacalności inwestycji przepływy pieniężne obejmują:

• inwestycyjne przepływy pieniężne,

• operacyjne przepływy pieniężne możliwe do osiągnięcia z danego przedsięwzięcia.

Inwestycyjne przepływy pieniężne obejmują:

• wydatki na przedmiot inwestycji,

• przyszłą wartość umorzeniową (likwidacyjną) przedmiotu dzisiejszych nakładów inwestycyjnych.

Operacyjne przepływy pieniężne obejmują:

• planowaną wartość sprzedaży,

• prognozowany poziom kosztów operacyjnych (wraz z kosztami amortyzacji przedmiotu inwestycji),

• zysk operacyjny po opodatkowaniu,

• wartość amortyzacji przedmiotu inwestycji jako wpływ gotówkowy,

• zmiany w wartości składników kapitału obrotowego netto, czyli wydatki, jakie firma ponosi, aby zwiększyć swoje aktywa obrotowe (zapasy, należności) ponad zobowiązania krótkoterminowe. Zmiany w kapitale obrotowym, można zapisać w następujący sposób:

∆ kapitał obrotowy = ∆ zapasów + ∆ należności - ∆ zobowiązania krótkoterminowe

Schemat ustalania przepływów pieniężnych

1. METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH

Oceniając opłacalność projektów inwestycyjnych wykorzystuje się mierniki finansowe zaliczane do grupy:

• metod prostych,

• metod dyskontowych.

Metody proste oceniają opłacalność inwestycji w oparciu o prognozowane przepływy pieniężne bez uwzględnienia zmian wartości pieniądza w czasie. Do metod prostych zalicza się miedzy innymi:

• okres zwrotu nakładów inwestycyjnych (Payback Period - PP),

• księgową stopę zwrotu (Accounting Rate of Return - ARR).

Metody dyskontowe analizują opłacalność przedsięwzięcia inwestycyjnego bazując na zaktualizowanych (dyskontowanych) wartościach przyszłych przepływów pieniężnych możliwych do osiągnięcia z danego projektu inwestycyjnego (zdyskontowane przepływ pieniężne uwzględniają czynnik zmiany wartości pieniądza w czasie). Do tych metod zalicza się:

• wartość obecną netto (Net Present Value - NPV)

• wewnętrzną stopę zwrotu z inwestycji (Internal Rate of Return - IRR)

1. Metody proste

Okres zwrotu nakładów inwestycyjnych

Okres zwrotu nakładów inwestycyjnych oznacza czas w jakim środki finansowe zaangażowane w przedsięwzięcie zostaną pokryte przez nadwyżki finansowe, których oczekuje się dzięki realizacji danego projektu.

Przy wyborze wariantu inwestycyjnego należy kierować się minimalizacją okresu zwrotu nakładów inwestycyjnych. Zaletą kryterium okresu zwrotu jest prostota obliczeń. Podstawowe wady tej metody polegają na tym, że nie bierze ona pod uwagę całego okresu funkcjonowania projektu oraz nie uwzględnia zmiany wartości pieniądza w czasie.

Zadanie 1

Pewne przedsiębiorstwo rozważa możliwość podjęcia realizacji projektu inwestycyjnego, wymagającego 100 000 PLN nakładów. Oblicz okres zwrotu dla tego projektu jeżeli wiadomo, że w kolejnych latach generuje on następujące przepływy pieniężne: CF₁ = 30 000 PLN, CF₂ = 50 000 PLN, CF₃ = 70 000 PLN, CF₄ = 20 000 PLN.

Księgowa stopa zwrotu

Księgową stopę zwrotu określa się jako przeciętną stopę zwrotu z inwestycji z całego okresu eksploatacji obiektu powstałego z inwestycji. Można ją wyznaczyć w następujący sposób:

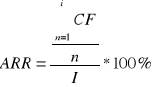
ARR - Księgowa stopa zwrotu,

CF - wolne środki wygenerowane przez projekt w i-tym okresie,

n - liczba okresów eksploatacji obiektu,

I - początkowy nakład inwestycyjny

Przy wyborze wariantu inwestycyjnego należy kierować się maksymalizacją wskaźnika ARR. Księgowa stopa zwrotu jest wygodnym narzędziem oceny projektów inwestycyjnych. Cechuje się dużą prostotą i łatwością obliczeń. Do wad tej metody należy zaliczyć przede wszystkim pomijanie czynnika czasu w analizie wartości wolnych środków generowanych przez projekt.

Zadanie 2

Możesz zrealizować jeden z dwóch projektów inwestycyjnych. Projekt A wymagający nakładów w kwocie 10 000 PLN i generujący w kolejnych latach następujące przepływy pieniężne: CF₁ = 3 000 PLN, CF₂ = 4 000 PLN, CF₃ = 5 000 PLN, lub Projekt B wymagający nakładów w kwocie 15 000 PLN i generujący w kolejnych latach przepływy pieniężne w wysokościach CF₁ = 3 000 PLN, CF₂ = 4 000 PLN, CF₃ = 8 000 PLN. Na podstawie księgowej stopy zwrotu dokonaj wyboru lepszego wariantu inwestycyjnego.

2. Metody złożone

Wartość obecna netto (NPV)

Wartość obecna netto (NPV - Net Present Value) mierzy nadwyżkę sumy zdyskontowanych wpływów nad sumą zdyskontowanych wydatków. Liczona jest ona według następującej formuły:

gdzie:

NPV - wartość bieżąca netto,

CF_i - przyszłe wolne przepływy pieniężne netto, w kolejnych okresach eksploatacji inwestycji,

I - początkowe nakłady inwestycyjne,

r - stopa dyskontowa (wymagana stopa zwrotu, koszt kapitału dla konkretnego przedsięwzięcia),

n - liczba przewidywanych okresów prognozy finansowej dla danej inwestycji.

Jeżeli wartość NPV dla danego projektu jest dodatnia to dany projekt należy zaakceptować do realizacji, gdyż generuje on sumę wartości zaktualizowanych przepływów pieniężnych wyższą od początkowego nakładu kapitałowego.

Jeżeli wartość NPV dla danego projektu jest ujemna to dany projekt należy odrzucić, gdyż nie generuje nadwyżki finansowej.

Przy wyborze najlepszego wariantu inwestycyjnego kierujemy się kryterium maksymalizacji wartości NPV (wybieramy projekt inwestycyjny charakteryzujący się wyższym NPV).

Zadanie 3

Na podstawie wartość obecnej netto (NPV) wybierz jeden spośród dwóch projektów inwestycyjnych. Zarówno projekt A, jak i projekt B wymagają zaangażowania 100 000 PLN. Projekty te mogą w kolejnych latach wygenerować następujące wolne przepływy pieniężne:

Nakład inwestycyjny może być sfinansowany kapitałami o średnim koszcie ich pozyskania równym 15% rocznie (oczekiwana stopa zwrotu z przedsięwzięcia).

Wewnętrzna stopa zwrotu (IRR)

Przez wewnętrzną stopę zwrotu (IRR - Internal Rate of Return) rozumie się taka wartość stopy dyskontowej, dla której wartość bieżąca netto (NPV) jest równa zeru. Wartość wewnętrznej stopy zwrotu (IRR) można wyznaczyć, przyrównując do zera formułę na NPV.

Wewnętrzna stopa zwrotu (IRR) może przyjmować wartości z trzech przedziałów (r - koszt kapitału, oczekiwana stopa zwrotu):

1. r < IRR - przy danym koszcie kapitału (r) projekt generuje dodatnią wartość bieżącą netto (NPV). Projekt można zaakceptować.

2. r = IRR - przy danym koszcie kapitału (r) projekt jest neutralny. Nie zmniejsza ani nie zwiększa zasobów gotówkowych. Projekt generuje zerową wartość bieżącą netto (NPV).

3. r > IRR - przy danym koszcie kapitału (r) projekt generuje ujemną wartość bieżącą netto (NPV). Projekt należy odrzucić.

Zadanie 4

Oblicz wewnętrzną stopę zwrotu (IRR) dla projektu wymagającego nakładów inwestycyjnych w kwocie 50 000 PLN, jeżeli wiadomo, że projekt w kolejnych latach wygeneruje następujące przepływy pieniężne:

Zależność między wartością bieżącą netto i wewnętrzną stopą zwrotu

W praktyce często mamy do czynienia z wyborem jednego z dwóch (lub kilku) projektów inwestycyjnych. W takiej sytuacji należy posłużyć się jednocześnie dwoma kryteriami: NPV oraz IRR.

Analiza opłacalności dwóch projektów może wykazać, że pierwszy projekt generuje wyższą wartość obecną netto niż projekt drugi, ale projekt drugi charakteryzuje się wyższą wewnętrzną stopą zwrotu, niż projekt pierwszy. W tej sytuacji podstawowego znaczenia nabiera wyznaczenie punktu przecięcia wykresów NPV dla dwóch projektów inwestycyjnych. Punkt ten, nazywany punktem Fishera, można wyznaczyć rozwiązując następujące równanie:

NPV 1 = NPV 2

gdzie:

NPV 1 - wartość bieżąca netto (NPV) pierwszego projektu,

NPV 2 - wartość bieżąca netto (NPV) drugiego projektu.

Zależność między wartością obecna netto (NPV) oraz wewnętrzną stopą zwrotu (IRR) dla dwóch projektów inwestycyjnych przedstawia poniższy wykres (NPV - wartość obecna netto, r- stopa dyskontowa). Przy stopie dyskontowej równej r₁ występuje punkt Fishera.

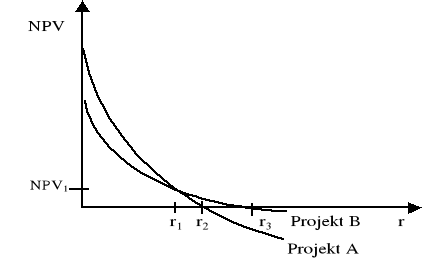
Analizując powyższy wykres można wyróżnić trzy sytuacje:

1. dla 0 < r < r₁ wybierając projekt A osiągniemy wyższą wartość NPV, niż wybierają projekt B.

2. dla r₁< r < r₃ należy wybrać projekt B. Wybierają projekt A osiągniemy niższą wartość NPV niż wybierając projekt B lub (dla r > r₂) projekt A przyniesie nam straty,

3. dla r > r₃ należy odrzucić oba projekty, gdyż generują ujemną wartość obecną netto.

Zadanie 5

Dokonaj wyboru bardziej opłacalnego projektu inwestycyjnego biorąc pod uwagę kryterium NPV i IRR. Każde z przedsięwzięć wymagałoby nakładu kapitałowego równego 200 000 PLN. Powyższe projekty inwestycyjne charakteryzują się następującymi planowanymi przepływami pieniężnymi.

Analizę przeprowadź w dwóch wariantach. Pierwszym zakładającym, że koszt kapitału wynosi 10% i drugim zakładającym koszt kapitału na poziomie 20%.

Zadania 6

Planujesz otworzyć działalność gospodarczą polegającą na produkcji okien. Chcąc rozpocząć produkcję musisz wybudować halę produkcyjną oraz zakupić niezbędne maszyny. Hala powinna mieć powierzchnię 250 m², a szacowana wartość wybudowania jednego metra hali wynosi 2 000 PLN. Hala zostanie wybudowana na gruntach należących do Ciebie. W celu rozpoczęcia produkcji musisz zakupić 10 maszyn po 10 000 PLN każda (koszt maszyny uwzględnia koszty transportu oraz instalacji). Hala produkcyjna ma okres amortyzacji wynoszący 20 lat, natomiast maszyny amortyzują się przez okres 5 lat.

Planuje się, że w pierwszym roku realizacji inwestycji wielkość produkcji wyniesie 500 sztuk okien. W kolejnych latach będzie rosła o 10% rocznie. Przez cały okres eksploatacji inwestycji planowana cena sprzedaży jednego okna będzie utrzymywała się na poziomie 500 PLN za sztukę. Koszty stałe (bez amortyzacji) będą wynosiły 10 000 PLN rocznie, natomiast koszty zmienne będą stanowiły 60% wartości przychodów ze sprzedaży. Zapotrzebowanie na kapitał obrotowy stanowić będzie 10% planowanej wartości sprzedaży. Stopa podatku dochodowego wynosi 19%. Przygotuj inwestycyjne oraz operacyjne przepływy pieniężne na okres trzech lat dla opisanego projektu. Oceń opłacalność inwestycji posługując się kryterium NPV. Koszt kapitału wynosi 10%.

Andrzej Rutkowski, Zarządzanie finansami, Polskie Wydawnictwo Ekonomiczne, Warszawa 2003, s. 209

Piotr J. Szczepankowski, Zarządzanie finansami przedsiębiorstwa. Podstawy teoretyczne, przykłady i zadania, Warszawa, WSPiZ 2004, s. 212

Andrzej Rutkowski, Zarządzanie finansami, Polskie Wydawnictwo Ekonomiczne, Warszawa 2003, s. 221

1

---