Metody modelowania układów dynamicznych

Wielkość wejściowa: Q(t) - wlew i wylew wody w zbiorniku

Wielkość wyjściowa: h(t) - wysokość słupa wody w zbiorniku, która wpływa na całkowite Q(t)

Celem ćwiczenia laboratoryjnego było zamodelowanie układu inercyjnego, którego przykładem był zbiornik Q₁ napełniany wodą. Zbiornik ów, wyposażony był we wlew Q_1we i wylew płynów Q_1wy. W początkowej fazie działania układu Q_1we>Q_1wy, do momentu, kiedy wysokość słupa wody h (wywierane ciśnienie) spowoduje stabilizacje słupa wody w zbiorniku, i wówczas Q_1we=Q_1wy. Jest to przykład idealnego układu inercjalnego idealnego. Do naszego układu dodaliśmy zbiornik Q₂, wyposażony tylko we wlew Q_2we, przez który wlewa się woda ze zbiornika Q₁. Jest to układ z członem całkującym z inercją (rzeczywisty).

Transformata Laplace'a

Operator przekształcający sygnał f(t) na pewną funkcję zespoloną F(s). Własności transformaty Laplace'a wykorzystane w tym ćwiczeniu:

1. Twierdzenie o różniczkowaniu:

2. Twierdzenie o całkowaniu:

Dla naszego przykładu k=1.

Równanie różniczkowe

Transmitancja operatorowa

Równanie różniczkowe

Transmitancja operatorowa

Aby wyznaczyć charakterystyki częstotliwościowe musimy wprowadzić pojęcie transmitancji widmowej która przedstawia się następująco:

przy czym:

Moduł
i argument
wyznaczamy z zależności:

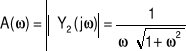
Charakterystyki częstotliwościowe

Rysunek układu

x(t) - ky(t)

-

y(t)

u(t)

s^-1

s^-1

x(t)

Charakterystyka fazowo-amplitudowa

Schemat układu zbudowanego w Simulink'u

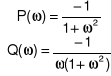
k