Zadania i metody automatycznej regulacji

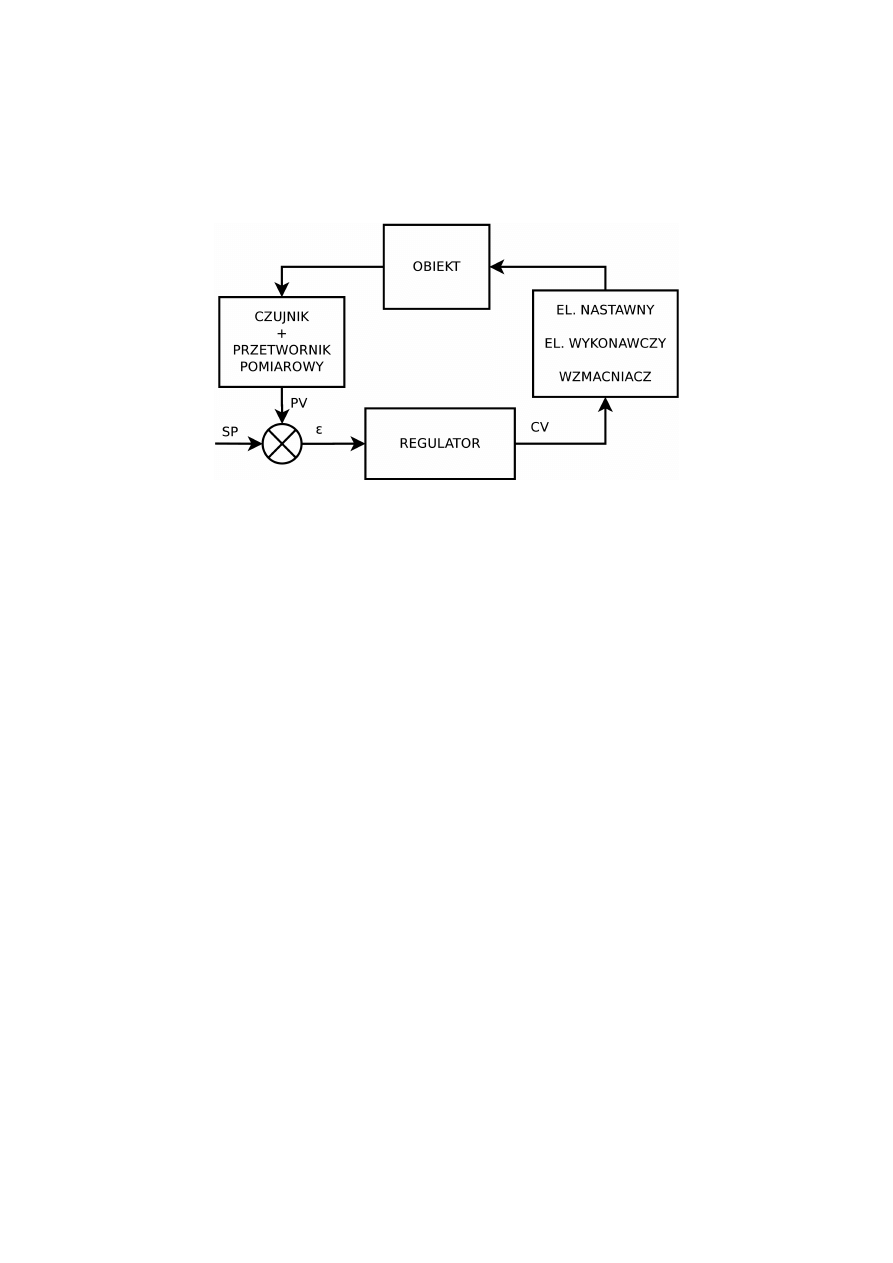
Regulacja   automatyczna  to   sterowanie   samoczynne   w   układzie   zamkniętym   czyli 

samoczynne utrzymywanie wymaganych sygnałów wejściowych obiektu. Regulacja ma za zadanie 

zminimalizowanie wpływu zakłóceń na układ.

W pętli występują wielkości:

•

SP – wartość zadana

•

PV – wartość procesowa

•

CV – zmienna sterująca

•

 – uchyb

ε

Regulator PID

Regulatorem najczęściej stosowanym w pętli jest 

regulator PID. Najczęściej występuje on 

w konfiguracji PID­IND, w której sygnał uchybu jest podawany na trzy niezależne tory, których 

wyjścia są sumowane. Występują w nim:

•

człon proporcjonalny – najprostszy, brak właściwości dynamicznych. Obwód regulacji z 
tylko   tym   członem   charakteryzuje   się   obecnością   uchybu.   Tor   opisywany   parametrem 

wzmocnienia k

p

.

•

człon   całkujący   –   regulator   używający   tego   członu   zapewnia   zerowy   uchyb   w   stanie 
ustalonym. Pogarsza on właściwości dynamiczne regulatora. Parametr: czas zdwojenia t

i

.

•

człon różniczkujący – reaguje on na zmianę uchybu, poprawia szybkość reakcji regulatora. 

Opisywany czasem wyprzedzenia t

d

.

Metody doboru nastaw regulatora PID

Do   doboru   regulatora   i   jego   dostrojenia   potrzebna   jest   znajomość   cech   statycznych   i 

dynamicznych obiektu, oraz kryterium pozwalające oceniać i porównywać uzyskane wyniki. Ważny 

jest również charakter działających na układ zakłóceń.
Metody eksperymantalne:

•

I metoda Zieglera­Nicholsa – metoda  

wzmocnienia krytycznego. Polega na zwiększaniu 

wzmocninia w członie proporcjonalnym, który jest jedynym aktywnym torem regulatora, aż 

do powstania stałych oscylacji. Autorzy metody podali wzory, które na podstawie wartości 
wzmocnienia   oraz   okresu   drgań   pozwalają   wyznaczyć   parametry   nastaw   regulatora 

Układ regulacji z zamkniętą pętlą

P/PI/PID. Metoda ta może być zbyt niebezpieczna w przypadku pewnych układów.

•

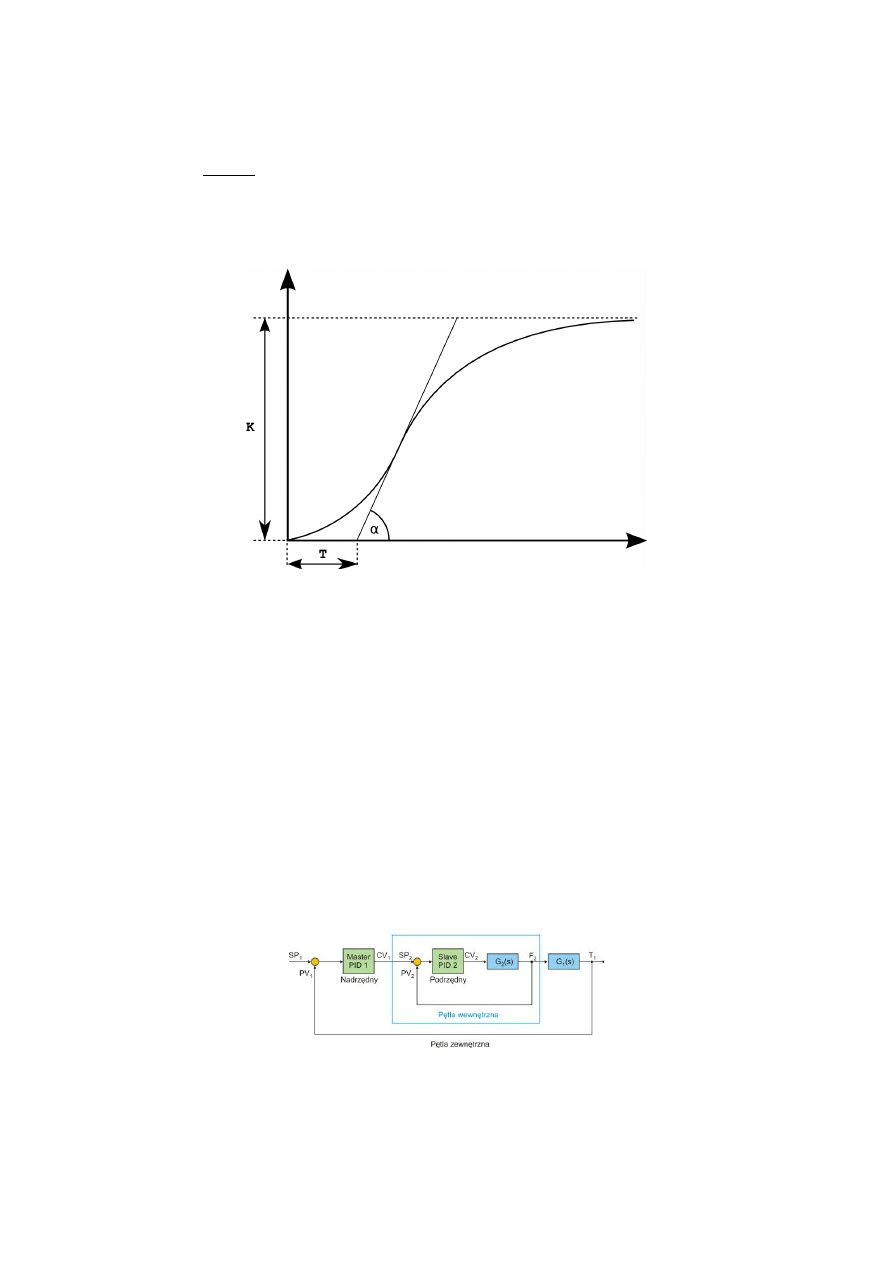
II   metoda     Zieglera­Nicholsa   –   W   tej   odmianie   metody   parametryzuje   się   układ   jako 
składający   się   z   członu   inercyjnego   o   stałej  T

i

  razem   z   opóźnionieniem   o   czas  T:

G s=

K

T

i

s1

e

−

Ts

. Polega ona na zbadaniu  

odpowiedzi skokowej  układu. Z wykresu 

odczytuje   się   parametry   wzmocnienia  K  oraz   współczynnik   kierunkowy   tg(a)   prostej 
przechodzącej przez punkt przegięcia krzywej. Na tej podstawie wyznacza się parametry 

regulatora.

Inne typy regulatorów

Kaskada

Składa się z dwóch obwodów sprzężenia, w której wartość sterująca pętli zewnętrznej jest 

wartością   zadaną   pętli   wewnętrznej.   Stosuje   się   ją   w   przypadku   obiektów   w   których   można 

wydzielić   procesy   o   znacznie   różniącej   się   inercji.   Za   zakłócenia   o   częstotliwości   wyższej 
odpowiada   pętla   wewnętrzna,   za   długoterminowe   pętla   zewnętrzna.   Przykład:   duży   obiekt 

ogrzewany przepływającym czynnikiem, sterowanie odbywa się otwarciem zaworu. Za ustalenie 
wartości otwarcia zaworu odpowiada pętla wewnętrzna, a zadaną wartość przepływu generuje pętla 

zewnętrzna. 
Regulator wewnętrzny jest najczęściej tylko proporcjonalny, ponieważ uchyb jest kompensowany 

przez pętlę zew., a szybkozmienne zakłócenia, które eliminowałby tor różniczkujący, są pochłaniane 
przez obiekt o dużej inercji.

Regulator dwu­ i trójstanowy

Regulator dwustanowy posiada dwa aktywne stany. Najczęściej jest to stan aktywny oraz brak 

sterowania. Działa on na zasadzie porównywania sygnału wejściowego z ustawionym progiem. W 
zależności od tego czy sygnał jest większy czy mniejszy przyjmuje on odpowiedni stan. Używa się 

ich   np.   w   termostatach,   układach   napełniających   zbiorniki   do   pewnego   poziomu.   Po   podaniu 

przebiegu trójkątnego jako progu regulator ten może zamieniać ciągły sygnał sterujący z innego 
regulatora na przebieg prostokątny zmodulowany PWM. Jest to użyteczne w przypadku elementu 

wykonawczego   który   może   znajdować   się   w   tylko   dwóch   stanach.   Rozszerzeniem   regulatora 
dwustanowego jest dodanie trzeciego stanu aktywnego, najczęściej o przeciwnym znaku do stanu 

pierwszego. 

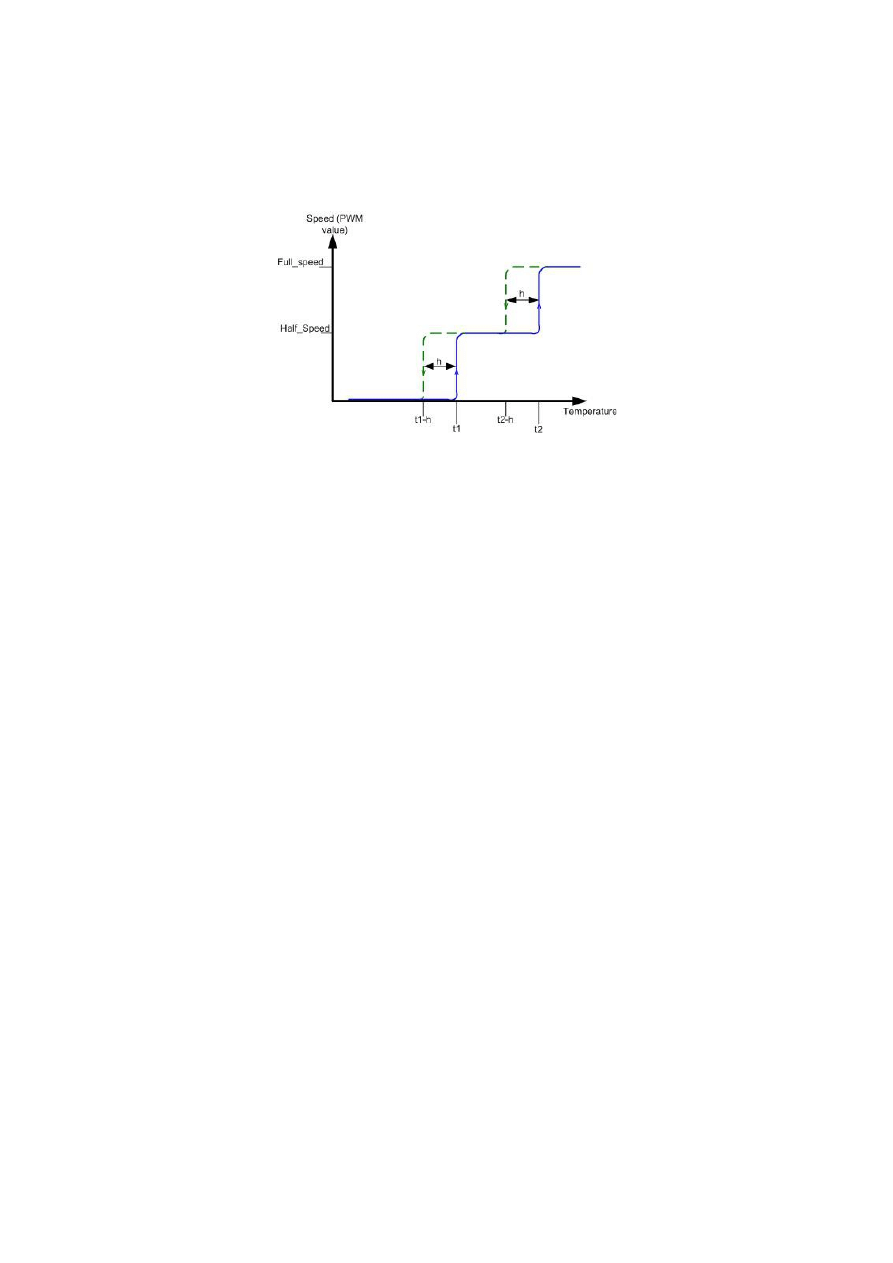
Aby   zapobiec   częstemu   przełączaniu   regulatorów   stosuje   się   histerezę.   Polega   ona   na 

przesuwaniu progów przełączania w zależności od  bieżącego stanu układu.

Po sprzężeniu regulatora trójstanowego z elementem całkującym sterowanie, jak silnik albo 

siłownik,  otrzymuje  się  

regulator kroczący. Jako jego wyjście traktuje się położenie które w 

przeciwieństwie   do   wyjścia   samego   regulatora   jest   sygnałem   ciągłym.   Przykładem   jest 
serwomechanizm albo pozycjoner.

Regulator z logiką rozmytą

Koncepcja logiki rozmytej (fuzzy logic) powstała w latach 60, zaproponowana przez Lotfi Zadeha. 
Znalazła zastosowanie w automatyce. Sygnał w regulatorze ulega następującym procesom:

•

Rozmywanie (fuzyfikacja) – sygnał ulega rozmyciu, czyli rozbiciu na funkcje przynależności

•

Wnioskowanie (interferencja) – na podstawie bazy reguł (przesłanek) zostaje wypracowana 

wynikowa   funkcja   przynależności.  Przesłanki   powstają   na   bazie   doświadczeń   osoby 
zajmującej się danym procesem.

•

Ostrzenie (defuzyfikacja), zamiana obliczonego sygnału na sygnał wyjściowy(sterujący)

Algorytm predykcyjny Smith'a

Regulator z predykcją został wymyślony przez Otto J. M. Smitha w roku 1957. Stosuje się go 

w   przypadku   regulacji   obiektów   z   dużym   opóźnieniem.   Do   działania   wymaga   on   znajomości 

modelu układu oraz czasu opóźnienia reakcji na sterowanie.

Przykład histerezy w regulatorze trójstanowym

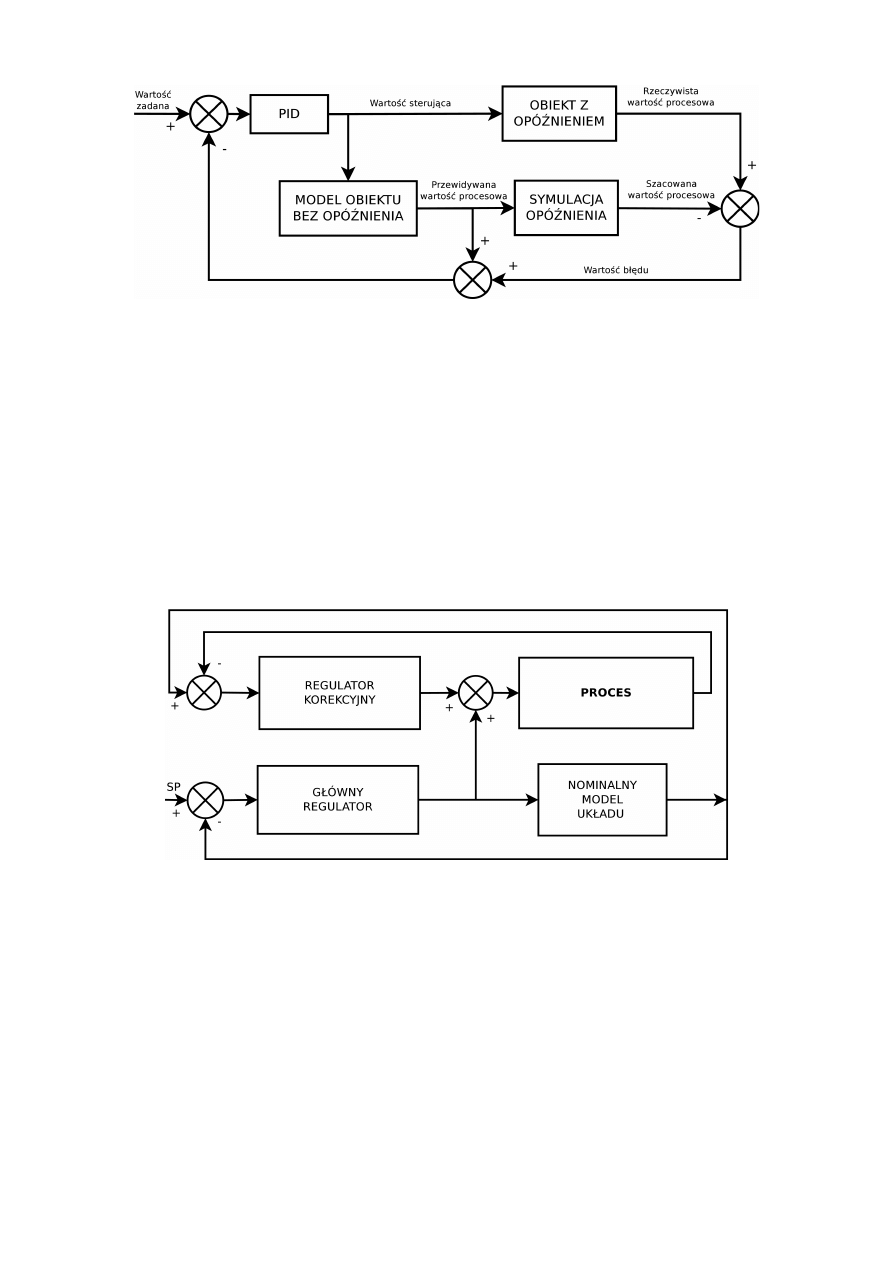
W   strukturze   predyktora   znajduje   się   gałąź   symulująca   odpowiedź   układu   na   bieżące 

sterowanie,   dzięki   czemu   regulator   nie   musi   czekać   na   informację   zwrotną   z   obiektu.   Wpływ 
zakłóceń jest brany pod uwagę poprzez odjęcie od bieżącej wartości procesowej jej obliczonego 

odpowiednika i dodanie błędu do wartości przewidywanej.

Układ regulacji z modelem

Układ   regulacji   z   modelem   (Model   Following   Controller)   zakłada   zmianę   parametrów 

obiektu   w   czasie   działania.   W   swojej   strukturze   posiada   on   dodatkowy   Regulator   Korekcyjny 
reagujący na te zmiany. Cechą charakterystyczną tego układu regulacji jest to, że proces rzeczywisty 

jest   sterowany   sumą   sygnałów   regulatora   korekcyjnego   oraz   regulatora   głównego.   Zaletą   tego 
rozwiązania jest to że dzięki właściwościom adaptacyjnym nie trzeba znać precyzyjnych wartości 

parametrów modelu.

Schemat predyktora Smith'a

Schemat układu regulacji z modelem (MFC)

Klasyfikacja obiektów

Obiekty   regulacji   klasyfikuje   się  zwykle   ze   względu   na   ich  własności   dynamiczne. 

Podstawowym   kryterium   podziału   obiektów   regulacji   jest   samodzielne   osiąganie   stanu   trwałej 

równowagi   po   wprowadzeniu   skokowego   wymuszenia   sygnału   wejściowego.   Zgodnie   z   tym 
kryterium rozróżnia się dwie grupy obiektów:

•

Obiekty astatyczne (bez samowyrównania) – wartość ich owpowiedzi skokowej dąży do 

nieskończoności, posiadają one właściwości całkujące (np. zbiornik cieczy)

•

Obiekty statyczne (z samowyrównaniem) – dzieli się je na
◦

proporcjonalne–odpowiedź skokowa jest także skokiem, opisuje się je wzmocnieniem K

◦

inercyjne I rzędu – parametr to wzmocnienie oraz stała czasowa T: G s=

K

Ts1

◦

inercyjne I rzędu z opóźnieniem – posiadają opóźnienie T

0

 : Gs=

K

Ts1

e

−

T

0

s

◦

inercyjne wyższego rzędu – są złożeniem n układów I rzędu, w praktyce modeluje się je 

także jako układ I z opóźnieniem, po wyznaczeniu opóźnienia zastępczego

Metody identyfikacji obiektu

•

badanie charakterystyki czasowej odpowiedzi układu na znany sygnał wejściowy (prostsza 
metoda), podać można:

◦

sygnał losowy (stochastyczny)

◦

skok (np. 5­>15% zakresu sygnału) , zastosować można aproksymację:

▪

Küpfmüllera – wyznacza parametry modelu inercyjnego I rzędu z opoźnieniem

▪

Strejca   –   parametry  K,T,n oraz τ  modelu   wyższego   rzędu   z   opóźnieniem   o 

transmitancji  Gs=

K



Ts1

n

e

−

s 

◦

impuls (np. w zakresie 15­25 %)

•

wyznaczenie charakterystyki częstotliwościowej układu – zbadanie zmian wprowadzanych 
przez obiekt w poszczególnych harmonicznych sygnału pobudzającego

•

porównanie z modelem strojonym – jeżeli znana jest klasa modelu do którego należy obiekt, 

można   manipulować   parametrami   posiadanego   modelu   aż   do   uzyskania   jednakowych 
odpowiedzi z obiektem