Badanie efektu Halla (ćwiczenie 24)
Cel ćwiczenia:
Celem ćwiczenia jest wyznaczenie parametrów mikroskopowych półprzewodników w oparciu o zjawisko Halla, wyznaczenie koncentracji nośników n. Badamy także zależność napięcia Halla (Uh) od natężenia prądu sterującego (Is).
Podstawy teoretyczne:
Jeżeli w polu magnetycznym umieścimy przewodnik lub półprzewodnik z prądem to na ładunki poruszające się w nim zadziała siła Lorenza, której zwrot można ustalić przy pomocy zasady lewej ręki. Ładunki są spychane i gromadzą się na powierzchni bocznego przekroju warstwy do czasu aż siła Lorenza nie zostanie zrównoważona przez działanie pola elektryczego.
Obserwację tego oddziaływania na nośniki prądu w ciele stałym najdogodniej jest przeprowadzić na próbce zwanej halotronem. Jeżeli przyjmiemy prostopadły układ osi XYZ(patrz rys.1) skierowanych równolegle do krawędzi halotronu oraz kierunek przepływu prądu sterującego będzie równoległy do osi X, a linie indukcji magnetycznej będą równoległe do osi Z, wtedy na ściance równoległej do płaszczyzny XZ gromadzą się nośniki, zaś na przeciwległej powierzchni stwierdzamy ich niedomiar. Powstaje wtedy różnica potencjałów zwana napięciem Halla. Wartość napięcia Halla ustala się samoczynnie w wyniku wytworzenia stanu równowagi pomiędzy siłą Lorentza, a siłą pochodzącą z powstającego pola poprzecznego
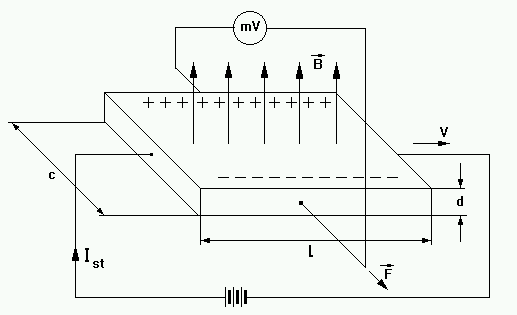
d -grubość warstwy
c- szerokość warstwy
l -długość warstwy
rys.1
Wykonanie ćwiczenia:
Badanie zależności napięcia Uh od prądu sterującego Is
B=(250±10)mT
klasa dla zakresu Is=2V to 0,5% rdg ± 1dgt
klasa dla zakresu Uh=2V to 0,3% rdg ± 1dgt
Is[mA] |
Uh[mV] |
9,00±0,06 8,50±0,05 8,00±0,05 7,50±0,05 7,00±0,05 6,50±0,04 6,00±0,04 5,50±0,04 5,00±0,04 4,50±0,03 4,00±0,03 3,50±0,03 3,00±0,03 |
977±3 827±3 781±2 731±2 685±2 637±2 589±2 541±2 493±2 444±1 395±1 346±1 296±1 |
Wyznaczenie współczynnika kierunkowego funkcji na podstawie pomiarów:
1 pomiar największy
A'(9,06[mA] ; 980[mV])
B' 2 B'(8,94[mA] ; 974[mV])
0' pomiar najmniejszy
A' A(2,97[mA];297[mV])
B(3,03[mA];295[mV])
A Równania prostych:
0
B
Uh= 112.15[mV/mA]∙Ist-36,08[mV] (a1=112,15[mV/mA] b1=-36,08 [mV]),
Uh=113,40[mV/mA]∙Ist--39,79 [mV] (a2=113,40 [mV/mA] b2=-39,79[mV])
ā=![]()
=112,78[mV/mA]
b=![]()
=37,94[mV]
Δā=![]()
=0,63[mV/mA]
Δb=![]()
=1,86[mV]
Dane do obliczenia koncentracji nośników:
grubość hallotronu: d = (100 ± 1) μm
szerokość: c = (2,5 ± 0,1) mm
długość: l = (10,0 ± 0,1) mm
ładunek elektronu: e = 1,6•10-19 [C]
indukcja B=(250±10)mT
Obliczenie wartości koncentracji nośników
![]()
gdzie ![]()
- współczynnik kierunkowy funkcji, więc ![]()
![]()
Błąd koncentracji:
![]()
![]()
![]()
Zadanie b)
Badanie zależności napięcia Uh od indukcji magnetycznej B
Wyniki pomiarów (przy IS=(9,5±0,06)[mA]:
(klasa dla zakresu Uh=2V to 0,3% rdg ± 1dgt, dla B 2,0% rdg ± 5dgt)
Uh[V] |
B[mT] |
0,904±0,004 0,885±0,004 0,866±0,004 0,844±0,004 0,821±0,003 0,800±0,003 0,778±0,003 0,755±0,003 0,733±0,003 0,710±0,003 |
74,92±1,55 73,33±1,52 71,77±1,49 69,93±1,45 68,03±1,41 66,29±1,38 64,47±1,34 62,56±1,30 60,74±1,26 58,83±1,23 |
Sporządzenie wykresów na podstawie danych z zadania a) i b)
Wnioski:
Wykresy sporządzone na podstawie danych uzyskanych w doświadczeniach prowadzą do wniosku iż zależność napięcia Halla od natężenia sterującego oraz zależność napięcia Halla od indukcji magnetycznej jest liniowa
Dla obliczonego współczynnika kierunkowego wykresu zależności napięcia Halla od natężenia sterującego, współczynnik koncentracji ładunków w próbce n jest równy:
![]()
4
Wyszukiwarka
Podobne podstrony:
Lab Fiz322a, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 31, Studia, II rok, Fizyka Eksperymentalna
Spr 42, Studia, II rok, Fizyka Eksperymentalna
Fizyka1, Studia, II rok, Fizyka Eksperymentalna
Cwiczenie 19, Studia, II rok, Fizyka Eksperymentalna
protokół fiza, Studia, II rok, Fizyka Eksperymentalna
Spr z fizy 35, Studia, II rok, Fizyka Eksperymentalna
FIZLAB~1, Studia, II rok, Fizyka Eksperymentalna
Spr 34, Studia, II rok, Fizyka Eksperymentalna
sprawozdanie z Halla, Studia, II rok, Fizyka Eksperymentalna
magnetyzm-nasze sprawko;), Studia, II rok, Fizyka Eksperymentalna
fiza, Studia, II rok, Fizyka Eksperymentalna
Lab Fiz364j, Studia, II rok, Fizyka Eksperymentalna
więcej podobnych podstron