Czym są macierze?

 

Macierz to po prostu tablica liczb.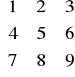
- jest to przykładowa macierz.

Dla macierzy ważne jest kilka wartości charakteryzujących ją:

• -         liczba wierszy (poziome)

• -         liczba kolumn (pionowe)

 

 Jeżeli w macierzy liczba kolumn jest równa liczbie wierszy to macierz nazywamy kwadratową n-tego stopnia, gdzie n to liczba kolumn i wierszy.

 

Każdy element macierzy jest opisywany przez numer wiersza i kolumny

np. a_i,j­ - oznacza element leżący w i-tym wierszu i j-tej kolumnie.

 

Definicja matematyczna:

 

Funkcję, która każdej parze liczb naturalnych przyporządkowuje dokładnie jedną wartość a_i,j ჎ R nazywamy macierzą

 

 

Macierze zapisujemy na ogół tłustym drukiem - A, B - opisujemy

A=[a_ij]_nxm - oznacza macierz o liczbie wierszy n i liczbie kolumn m, tworzą ją elementy a_ij

 

Macierz, której wszystkie elementy są równe zero, nazywamy macierzą zerową lub po prostu zerem, zapisujemy A=0

Dla macierzy kwadratowej możemy wyróżnić przekątną główną, tworzą ją elementy na przekątnej od lewego górnego rogu, do prawego dolnego. Matematycznie jest to ciąg elementów (a₁₁, a₂₂, ..., a_nn).

 

Macierz kwadratową, której wszystkie elementy oprócz przekątnej głównej są równe zero, nazywamy macierzą diagonalną i zapisujemy

diag(a₁₁,a₂₂,...,a_nn).

 

Macierz diagonalną, której wszystkie elementy na przekątnej równe są 1 nazywamy macierzą jednostkową lub po prostu jedynką i oznaczamy I.

 

np. I=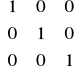
dla stopnia trzeciego

Macierz, która oprócz przekątnej ma same 0, a na przekątnej te same wartości nazywamy macierzą skalarną.

np. A=diag(a,a,a) =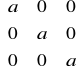

Mnożenie macierzy

 

 

Mnożenie macierzy nie jest już taką prostą sprawą. Operacja z początku może wydać się skomplikowana, ale po krótkiej wprawie wykonuje się ją już mnemotechnicznie.

 

Najpierw potrzebujemy zdefiniować sobie iloczyn skalarny dwóch wektorów.

 

Wektorem nazywamy macierz o jednej kolumnie.

 

Iloczynem skalarnym dwóch wektorów nazywamy liczbę która jest sumą iloczynów odpowiednich składowych wektorów.

 

 

 

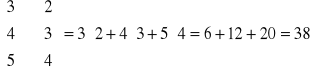
Mnożenie macierzy jest możliwe dla macierzy o odpowiednich wymiarach.

Jeżeli chcemy przeprowadzić mnożenie AთB to liczba kolumn macierzy A musi być równa liczbie wierzy macierzy B.

Mnożenie macierzy nie jest przemienne tzn. chcąc wykonać mnożenie

BთA liczba kolumn macierzy B musi być równa liczbie wierszy macierzy A.

 

 

Co jest wynikiem mnożenia?

 

 

Wynikiem mnożenia macierzy A_nxmთB_mxk jest macierz C o wymiarze nxk.

 

Czyli po prostu przy mnożeniu macierzy o wymiarach nxm przez macierz o wymiarach kxl

• -         po pierwsze „wewnętrzne” wymiary muszą się zgadzać => m=k

• -         wynikiem jest macierz o wymiarach nxl

 

 

Jaką postać będzie miała macierz C?

 

Otóż każdy element macierzy C - c_ij jest równy iloczynowi skalarnemu i-tego wiersza macierzy stojącej po lewej stronie znaku mnożnie, przez j-tą kolumnę macierzy stojącej po prawej stronie znaku mnożenia.

 

np.

 

 

 

 

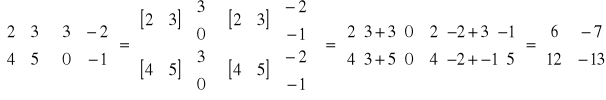
Definicja

Iloczynem macierzy A=[a_ij]_nxp przez macierz B=[b_ij]_pxm nazywamy taką macierz C=[c_ij]_nxm piszemy C=AთB, że

dla i=1,2,...,n;j=1,2,...,m

 

W ogólnym przypadku mnożenie macierzy nie jest przemienne, natomiast jeżeli AთB=BთA to macierze A i B nazywamy przemiennymi.

 

 

 

Kilka przydatnych właściwości:

 

Jeżeli A,B oraz C są macierzami o odpowiednich wymiarach to:

1. 1.    A(BC)=(AB)C

2. 2.    ၡ(AB)=(ၡA)B

3. 3.    (A+B)C=AC+BC

4. 4.    C(A+B)=CA+CB

5. 5.    IA=A, gdy A_nxn i I_nxn

 

I.                                      Porównywanie macierzy

 

 

Dla macierzy A=[a_ij]_nxm oraz B=[b_ij]_nxm możemy stwierdzić równość jeżeli odpowiadające sobie elementy są równe.

 

Matematycznie zapisujemy:

A=B a_ij=b_ij dla (i=1,2,...,n;j=1,2,...,m)

 

 II.                                 Dodawanie macierzy

 

 

Dodawanie (i analogicznie odejmowanie) macierzy jest możliwe tylko dla dwóch macierzy o takich samych wymiarach. Wynikiem dodawania macierzy jest macierz o takich samych wymiarach jak składniki. Elementy macierzy wynikowej są sumą odpowiednich elementów składników.

 

Matematycznie zapisujemy:

A=[a_ij]_nxm , B=[b_ij]_nxm

Sumą macierzy A+B nazywamy taką macierz C = [c_ij]_nxm , że:

c_ij=a_ij+b_ij dla (i=1,2,...,n;j=1,2,...,m)

 

czyli po prostu:

C=A+B= [a_ij+b_ij]_nxm

 

analogicznie definiujemy odejmowanie:

D=A-B= [a_ij-b_ij]_nxm

np.:

 

 

 

 

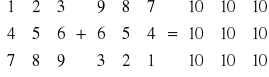
III.                            Mnożenie przez skalar

 

Każdą macierz możemy pomnożyć przez dowolną liczbę rzeczywistą. Mnożenie przez liczbę rzeczywistą polega na pomnożeniu każdego elementu przez tą liczbę. Mnożenie przez skalar jest przemienne.

 

Matematycznie

A=[a_ij]_nxm - iloczynem ၡთA nazywamy taką macierz C=[c_ij]_nxm, że:

c_ij=ၡთa_ij

 

np.

 

 

 

 

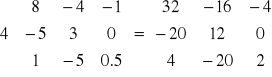
1. I.                           Transpozycja macierzy

 

 

Transpozycja jest operacją często używaną w obliczeniach na macierzach.

 

Operacja transpozycji to zamiana macierzy tak aby jej wiersze stały się kolumnami. Transpozycję oznaczamy indeksem górne T.

 

A^T - transpozycja macierzy A

 

np.

 

 

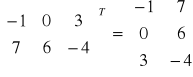
Matematycznie

 

 

Dla macierzy A=[a_ij]_nxm macierz B=[b_ij]_mxn taką, że:

b_ij=a_ji dla i=1,2,...,m; j=1,2,...,n nazywamy transpozycją macierzy A.

 

 

Z definicji transpozycji wynika kilka ciekawych właściwości:

 

 

Jeżeli A=[a_ij]_nxp oraz B=[b_ij]_pxm i ၡ jest liczbą, to:

1. (A^T)^T=(A)

2. (AB)^T=B^TA^T

3. (ၡA)^T=ၡ(A)^T

4. (A+B)^T=A^T+B^T, jeżeli wymiary macierzy A i B są takie same

 

 

 

2. II.                      Macierze ortogonalne

 

Macierz kwadratową A nazywamy ortogonalną, jeżeli

AA^T=I

 

Jeżeli macierz jest ortogonalna to również jej transpozycja jest ortogonalna

 

 

Macierz jest ortogonalna wtedy i tylko wtedy, gdy iloczyn skalarny dwóch wierszy (kolumn) tej macierzy był równy zeru, a iloczyn skalarny każdego wiersza (kolumny) był równy 1.

 

 

---