Minimalizacja funkcji logicznych i projektowanie układów kombinacyjnych

1. Sposoby opisu funkcji logicznych

2. Metody minimalizacji funkcji logicznych
   - Metoda tablic Karnaugha
   

1. Sposoby opisu funkcji logicznych

Funkcje logiczne definiują zależność sygnału wyjściowego od wartości zmiennych. Funkcje logiczne są pełną formą opisu działania układów kombinacyjnych (tzn. nie posiadających możliwości pamiętania swojego stanu).

Najczęściej stosowane są następujące formy funkcji:

Opis słowny

Spotyka się go w zasadzie wyłącznie we wstępnej fazie projektowania układu. Do dalszej analizy tworzy się na podstawie opisu słownego tabelę lub/oraz postacie kanoniczne.

Tabela funkcji.

Postać najczęściej spotykana, zwłaszcza dla funkcji niewielu zmiennych. W tabeli można uwzlędnić oprócz stanów 0 i 1 również stany nieokreślone, oznaczane zwykle - (minus) lub x.

Postać kanoniczna.

Jest to postać wynikająca z teorii algebry Boole'a. Występuje w dwóch formach:
- postać kanoniczna sumy KPS (stosowana częściej)
- postać kanoniczna iloczynu KPI

Wyrazy KPS są iloczynami wszystkich kombinacji zmiennych funkcji. Nazywane są implikantami.
Wyrazy KPI są sumami wszystkich kombinacji zmiennych funkcji. Nazywane są implicentami.

Implikanty i implicenty dla funkcji 3 zmiennych

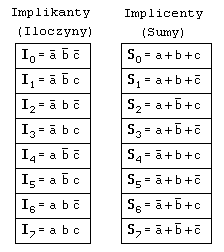
W implikantach:

wartości 0 odpowiada zmienna zanegowana

wartości 1 odpowiada zmienna podana wprost

W implicentach:

wartości 0 odpowiada zmienna podana wprost

wartości 1 odpowiada zmienna zanegowana

_ _ _

np: abc=011 (3) -> I3 = a b c S3 = a + b + c

_ _ _

abc=101 (5) -> I5 = a b c S5 = a + b + c

W KPS funkcja stanowi sumę iloczynów (implikantów) pomnożonych przez wartości funkcji. Implikanty dla 0 znikają:

Postać kanoniczna sumy

W KPI funkcja stanowi iloczyn sum (implicentów) z dodanymi wartościami funkcji. Implicenty dla 1 znikają:

Postać kanoniczna iloczynu

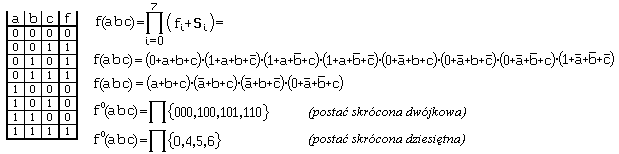
W praktyce najczęściej stosuje się postać skróconą KPS. W tym zapisie można również uwzględnić stany nieokreślone przez podanie indeksów tych stanów w nawiasach okrągłych:

Postać kanoniczna sumy ze stanami nieokreślonymi

do góry

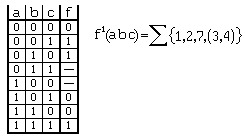
2. Metody minimalizacji funkcji logicznych

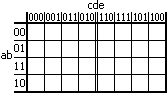
Metoda tablic Karnaugha

Jest to metoda graficzna. Jest wygodna dla funkcji od 2 do 6 zmiennych. Dla większej ilości zmiennych staje się zbyt trudna.

Metoda ta występuje w dwóch wersjach: dla postaci sumacyjnej oraz dla postaci iloczynowej. Poniżej omówiona jest metoda dla postaci sumacyjnej.

Postępujemy według następujących punktów:

1. Funkcję należy przedstawić w postaci kanonicznej lub tabelarycznej.

2. Tworzymy tabelę dla odpowiedniej ilości zmiennych

2 zmienne	3 zmienne	4 zmienne
	lub
5 zmiennych
lub

3. Wartości umieszczone z lewej strony i u góry oznaczają wartości podanych zmiennych

4. W kratki tabeli wpisujemy wartości funkcji ("0", "1" lub "-") zgodnie z postacią funkcji. Przykład: tabela Karnaugha

5. Dla funkcji F(abcd)=Σ{1,4,5,6,15,(7,9,10,14)}

6. 
   

7. Zakreślamy pola (grupy) w siatce tabeli zgodnie z następujacymi zasadami:

• Pole jest kwadratem lub prostokątem o bokach będących potęgą 2, tzn. 1, 2, 4, 8, ..

• Pola obejmują kratki sąsiednie, kratki skrajne (pola mogą być "zawinięte" przez brzeg tablicy), oraz w tabeli dla 5 zmiennych symetryczne względem podwójnej linii.

• Grupy muszą objąć wszystkie "1".

• Grupy nie mogą obejmować "0".

• Stany nieokreślone "-" mogą, ale nie muszą być zakreślane.

• Grupy powinny być jak największe.

• Ilość grup powinna być możliwie mała.

• Grupy mogą na siebie zachodzić.

Przykład: zakreślanie pól w tablicy Karnaugha

Dla funkcji F(abcd)=Σ{1,4,5,6,15,(7,9,10,14)}




8. Odczytu funkcji wykonujemy według zasad:

• Funkcja ma postać normalną sumy, tzn. suma implikantów prostych. W niektórych zastosowaniach wygodniej jest wypisać implikanty proste w postaci dwójkowej, np: 

abd- = (01-1)

• Jednemu polu odpowiada jeden implikant.

• Jeżeli zmienna przyjmuje dla danego pola wartość 1 to piszemy ją wprost.

• Jeżeli zmienna przyjmuje dla danego pola wartość 0 to piszemy ją z negacją.

• Jeżeli zmienna przyjmuje dla danego pola wartości 0 i 1 (zmienia wartość), to jej nie piszemy.

Przykład: odczytanie funkcji

Dla funkcji F(abcd)=Σ{1,4,5,6,15,(7,9,10,14)}

9. W razie potrzeby można dokonać dalszych przekształceń funkcji.

10. Schemat układu minimalnego (bez przekształceń). Przykład: schemat układu

Schemat układu realizującego funkcję:

F(abcd)=Σ{1,4,5,6,15,(7,9,10,14)}=

=ab+acd+bc-  --

do góry

---