METODY NUMERYCZNE

Elektrotechnika, rok II, sem. III

Data: 04.12.2009

ZADANIE PROJEKTOWE

ZESPÓŁ PRZYGOTOWUJĄCY ZADANIE PROJEKTOWE
L.p.	Nazwisko	Imię
I	Koziński	Grzegorz
II	Domagalski	Piotr

Dany jest układ regulacji automatycznej, przedstawiony na rysunku:

Wyznaczyć numeryczne rozwiązanie odpowiedzi układu y(t) na wymuszenie:
x(t) =1(t) stosując czteropunktową metodę Runge-Kutta. Przyjąć warunki początkowe: y(0)=1; y'(0)=y''(0)=0. Dane:

G₁(s)=
G₂(s)=

Przy czy:

a - liczba liter I imienia = 8

b - suma liter I i II nazwiska = 18

c - liczba liter II imienia = 5

Wyniki wykonać w Excelu: tabelarycznie i w postaci wykresów

Dane

G₁(s)=
G₂(s)=

a = 8 b = 18 c = 5

Warunki początkowe:

t_k=0 y=1 y'=0 y”=0 dla h=0,1

Układ otwarty

y(t)=x(t)*G₁(s)*G₂(s)

G(t)=

G(s)=

Układ zamknięty

y(t)=x(t)*G₁(s)*G₂(s)-y(t)*G₁(s)*G₂(s)

y(t)+y(t)*G₁(s)*G₂(s)=x(t)*G₁(s)*G₂(s)

=

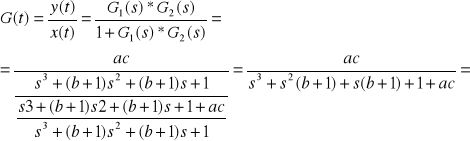
G(s)=

Równanie różniczkowe:

y(s)(s³+19s²+19s+41)=40x(s)

y'”(t)+19y”(t)19 (t)+41y(t)=40x(t)

z' z x

k y' = x

m x' = z

n z' = -19z-19x-41y+40

k₁ = hx_k

m₁ = hz_k

n₁ = h(-19z_k-19x_k-41y_k+40)

k₂ = h(x_k+m₁/2)

m₂ = h(z_k+n₁/2)

n₂ = h[-19(z_k+ n₁/2)-19(x_k+m₁/2)-41(y_k+k₁/2)+40]

k₃ = h(x_k+m₂/2)

m₃ = h(z_k+n₂/2)

n₃ = h[-19(z_k+ n₂/2)-19(x_k+m₂/2)-41(y_k+k₂/2)+40]

k₄ = h(x_k+m₃)

m₄ = h(z_k+n₃)

n₄ = h[-19(z_k+ n₃)-19(x_k+m₃)-41(y_k+k₃)+40]

y_k+1 = y_k+1/6(k₁+2k₂+2k₃+k₄)

x_k+1 = x_k+1/6(m₁+2m₂+2m₃+m₄)

z_k+1 = z_k+1/6(n₁+2n₂+2n₃+n₄)

Wykresy:

y_k = f(t_k) x_k = f(t_k) x_k = f(y_k)

G₁(s)

G₂(s)

y(t)

---