Nazwisko: Birunt
Imię: Wojciech
Kierunek: Fizyka z informatyką II
Rok studiów: 2000/2001r.
Grupa laboratoryjna: XI
|
WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie I PRACOWNIA FIZYCZNA |
||||
|
W y k o n a n o |
O d d a n o |
|||
|
Data
.III.2001r. |
Podpis |
Data
.III.2001r. |
Podpis |
|
Ćwiczenie nr
79 |
Temat: Badanie dyspersji szkła pryzmatu za pomocą goniometru optycznego |
||||
CZĘŚĆ TEORETYCZNA
Współczynnik załamania światła wyznaczyć możemy z kątów padania i załamania światła na granicy ośrodków. Najwygodniej w tym celu posługiwać się ciałem o specjalnie dobranym kształcie.
Najczęściej stosujemy pryzmat, który jest bryłą ograniczoną dwoma płaszczyznami tworzącymi ze sobą kąt ϕ, zwany kątem łamiącym. Kształt pozostałych ścian pryzmatu nie odgrywa istotnej roli. Promień świetlny padający na pryzmat zostaje odchylony o pewien kąt δ, zależny od kąta padania α i od kąta łamiącego ϕ.
Kąt δ jest najmniejszy gdy wewnątrz pryzmatu promień biegnie prostopadle do dwusiecznej kąta łamiącego. W tym przypadku kąt δ jest równy sumie kątów nie przyległych w trójkącie ABC, czyli:
δ= 2 (α - β)
Kąty β i ϕ/2 mają ramiona zgodnie prostopadłe, stąd β= ϕ/2 , ostatnie równanie przyjmuje postać;
α= (δ+ϕ)/2
![]()
Podstawiając wyrażenia na kąt padania α i załamania β do prawa załamania :
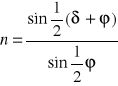
mamy:
Kąt łamiący ϕ określany jest precyzyjnie za pomocą spektrometru.
Wiązka padająca na pryzmat równolegle do dwusiecznej kąta łamiącego rozdziela się na dwie wiązki tworzące ze sobą kąt : ψ=2(αl+αp).
Kierunki promieni l i p mierzymy przez naprowadzenie lunety na kierunek l i p oraz odczyt jej położeń χl i χp na podziałce spektroskopu.
![]()
Kąt łamiący jest równy:
Wzór powyższy jest słuszny przy założeniu, że kąty χ mierzymy od kierunku promienia padającego (w prawo lub lewo).
Do dokładnego pomiaru kąta załamania światła w pryzmatach lub kąta ugięcia promieni ugiętych na siatce dyfrakcyjnej służą spektrometry zwane również goniometrami jednokołowymi.
Spektrometr składa się z następujących części : kolimatora, stolika, lunetki i kątomierza. Całość zamocowana jest na silnej podstawce.
Kolimator składa się z regulowanej szczeliny i soczewki. Długość kolimatora jest tak dobrana, że szczelina leży w ognisku soczewki, dzięki czemu otrzymujemy wiązkę równoległą. Kolimator jest nieruchomo związany z podstawką. Luneta połączona jest na stałe z kątomierzem i może obracać się wokół osi spektrometru, a jej położenie odczytuje się na kątomierzu z dokładnością równą niekiedy jednej minucie końcowej. Tak dokładny odczyt umożliwiają noniusze znajdujące się w odległości wzajemnej π. Luneta zbiera wiązkę równoległą światła dając tym samym ostry obraz szczeliny.
![]()
W nowych goniometrach kąty odczytuje się metodą optyczną, a precyzje tego odczytu jest bardzo duża. Położenie kątowe lunety jest równe średniej arytmetycznej wskazań l , p obu noniuszy:
Precyzyjne spektrometry zaopatrzone są ponadto w układ pokręteł służących do unieruchamiania lunety i stolika oraz do precyzyjnego przesuwania tych części.
Przebieg ćwiczenia.
Wyzerować goniometr wprowadzając zero skali na zerowe położenie lunety.
Uruchomić lampę helową.
Pomiar kąta łamiącego pryzmatu.
Ustawić na stoliku badany pryzmat w taki sposób, by światło z kolimatora białego w przybliżeniu padało równolegle do dwusiecznej kąta łamiącego.
Naprowadzić lunetę na kierunek promienia l odbitego od ściany pryzmatu i zanotować położenie lunety

ΦL . To samo zrobić dla promienia p notując kąt ΦP.Obliczyć kąt łamiący pryzmatu:
![]()
.
2. Pomiar kąta najmniejszego odchylenia i wyznaczanie współczynnika załamania.
Ustawić pryzmat w takim położeniu, by światło wchodzące z lampy helowej uległo załamaniu i przez lunetę można było obserwować jego widmo.
Obracać powoli stolik z pryzmatem tak, by obraz widma przesuwał się w stronę położenia zerowego lunety. Uchwycić moment, w którym obraz widma zatrzymuje się i zawraca mimo dalszego obracania pryzmatu w tym samym kierunku. W położeniu tym kąt odchylenia ma wartość najmniejszą δmin.
Ustawić lunetę na kierunek, w którym nastąpi moment zwrotny przesuwania się widma i odczytać na skali kąt jej ustawienia αP na wybraną linię widma.
Obrócić stolik i w analogiczny sposób odczytać kąt αL.
Obliczyć wartość minimalną kąta wychylenia z zależności:
![]()
.
Analogicznie wykonać pomiary δmin dla kilku innych linii widma.
Obliczyć współczynnik załamania n dla poszczególnych długości fal ze wzoru:
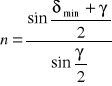
.
Wykonać wykres krzywej dyspersji materiału pryzmatu n = f(λ).
Tabela wyników.
![]()
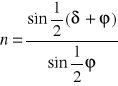
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Siatka dyfrakc-teoria, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr67
Dyspersja, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwiczenie n
Ćwiczenie nr 50b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr50b
Doświadczalne spr p. Malusa, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr70
Ćwiczenie nr 82, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr82
Ćwiczenie nr 65c, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65c
Ćwiczenie nr 65, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65
Oscyloskop, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr85
Goniometr - przebieg ćwiczenia, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Lab
53 wykres, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr53
Ćwiczenie nr 36, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr36
Ćwiczenie nr 8, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr8
Ćwiczenie nr 78, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr78
Wnioski do Ćw 65b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65b
Ćwiczenie nr 6, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr6
Ćwiczenie nr 73a, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr73a
Ćwiczenie nr 42, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr42
Ćwiczenie nr 11, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr11
Ćwiczenie nr 53, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr53
więcej podobnych podstron