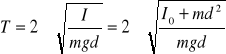W 1900 roku Max Planck przedstawił teorię, wg której promieniowanie elektromagnetyczne nie jest emitowane w sposób ciągły, ale w postaci ściśle określonych porcji energii, które nazwał kwantami. Energia kwantu jest wprost proporcjonalna do częstotliwości emitowanego promieniowania. E=h⋅ν h-stała Plancka; h=6,6249⋅10^-34 [J⋅s] Energia kwantu promieniowania elektromagnetycznego wyrażana jest zazwyczaj nie w dżulach, ale w elektronowoltach. Einstein wykorzystując pojęcie kwantu energii promieniowania elektromagnetycznego, wprowadził postulat zgodnie z którym energia fali świetlnej przenoszona jest w postaci oddzielnych kwantów energii, tzw. fotonów, oraz że w wyniku oddziaływania z elektronem, foton przekazuje elektronowi całą swoją energię. Wynikiem czego pomiędzy energią padającego fotonu a maksymalną energią kinetyczną fotoelktronów otrzymuje się prostą zależność, zwaną równaniem Einsteina-Milikana:hν = W +E_kmax (1)gdzie:W - bariera potencjału którą elektron musi pokonać aby opuścić powierzchnię danego materiału, czyli praca wyjścia elektronu z danego materiału.Jeżeli energia wiązania elektronu W równa pracy, jaką należy wykonać, aby wyrwać elektron z powierzchni płytki (tzw. praca wyjścia), jest większa od energii fotonu to zjawisko nie zajdzie. Zatem praca wyjścia jest równa energii fotonów światła o częstości równej częstości granicznej: W = hν_g Wykorzystując równanie Einsteina-Millikana można wyznaczyć stałą Plancka: h⋅ν=W+E_kmax Wnioskujemy więc, że stała Plancka określa stosunek energii fotonu światła do częstości fali świetlnej padającej na metal; wielkość tą określamy wzorem h = E_f/ν. Do wyznaczenia stałej Plancka wykorzystamy zjawisko fotoelektryczne zewnętrzne, polegające na emisji elektronów z metalu pod wpływem padającego światła.Źródłem światła monochromatycznego (Z) oświetlamy katodę (K) z której emitowane są elektrony. Pomiędzy fotokatodę i anodę przykładamy napięcie hamujące. Woltomierz mierzy napięcie hamujące natomiast amperomierz mierzy prąd anodowy. Maksymalna energia kinetyczna E_kmax=e⋅U_hm, gdzie e-ładunek elektronu; e=1,6⋅10^-19 C, natomiast przez U₀ oznaczymy wartość napięcia hamującego, przy którym prąd anodowy jest równy 0. Podstawiając e⋅U za E_kmax do równania Einsteina-Millikana otrzymujemy, że: U_hm= (h/e)⋅ν - (W/e) Wykres napięcia hamującego U₀ w funkcji częstotliwości ν jest funkcją liniową y=ax+b o współczynnikach a=h/e; b=-W/e. Znając a i b możemy wyznaczyć stałą Plancka oraz pracę wyjścia elektronu z metalu.

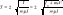
Wahadło Fizyczne - dowolne ciało sztywne, które pod wpływem własnego ciężaru wykonuje drgania wokół osi poziomej nie przechodzącej przez środek ciężkości ciała. Wychylenie wahadła o kąt ϕ powoduje, że pojawia się momentsiły M=d→×mg→ usiłujący przywrócić wahadłu położenie równowagi. Wartość liczbowa tego momentu M = -mgd sinα gdzie m jest masą wahadła, d -odległością od punktu zawieszenia do środka masy. Stosując druga zasadę dynamiki dla ruchu obrotowego, można zapisać I = -mgd sinα , gdzie I - moment bezwładności względem osi obrotu,  =d²ϕdt^  przyspieszenie kątowe. Widać, że w ogólnym przypadku ruch wahadła fizycznego nie jest ruchem harmonicznym. Jeżeli jednak ograniczymy się do małych kątów wychylenia, to sinα ≅ α i wówczas I*d²α/dt² = -mgdα, lub d²α/dt² = -(mgd/I)α. Przy takim założeniu ruch wahadła fizycznego jest ruchem harmonicznym, gdyż występuje liniowa zależność między kątem wychylenia i przyspieszeniem kątowym. Po przekształceniach otrzymujemy: ω² = mgd/I, stąd okres drgań wahadła fizycznego przy niewielkich wychyleniach wyraża się wzorem:

gdzie I₀ jest momentem bezwładności względem przechodzącej przez środek ciężkości i równoległej do osi wahań. Okres drgań zależy od odległości między punktem zawieszenia a środkiem ciężkości. Dla bardzo małych wartości d okres jest bardzo duży. Ze wzrostem d okres drgań maleje, osiągając minimum dla d = pierwiastek(I₀/m), następnie znów rośnie. Ruch harmoniczny - ruch w którym zmieniają się: położenie, prędkość i przyspieszenie. Gdy podczas tego ruchu nie mamy strat energii i nie ma sił oporu to wówczas mamy do czynienia z drganiami swobodnymi. Aby wywołać ruch drgający musi być spełniony warunek konieczny: - musi działać siła harmoniczna, która jest wprost proporcjonalna do wychylenia: F = -kx F = -k(x -x₀) k - współczynnik proporcjonalności F = -kx ma = -kx a = dv/dt = d²x/dt² m(d2x/dt2) = -kx d²x/dt² + (k/m)x = 0 k/m = ω d²x/dt² + ω²x = 0 - równanie różniczkowe II stopnia. Podczas drgań torsyjnych bryły sztywnej we wzorze F = -kx siłę F trzeba zastąpić momentem siły, który można wyrazić wzorem: M = - Dϕ.

Współczynnik proporcjonalności D o wymiarze Nm/rad nazywamy momentem kierującym. Korzystając z równania ruchu obrotowego bryły sztywnej moment siły można wyrazić wzorem: M = Iα, gdzie I - moment bezwładności, α - przyspieszenie kątowe, które definiuje się jako drugą pochodną kąta względem czasu: α = ∂²ϕ/∂t² Podstawiając ostatnie dwa wyrażenia do wzoru na moment siły otrzymujemy: (I∂²ϕ)/∂t² = -Dϕ i analogicznie równanie dla drgającego punktu o masie m, m∂²x/∂t² = -kx. Jeśli wprowadzimy oznaczenie ω²₀ = D/I lub ω²₀ = k/m, otrzymamy: ∂²ϕ/∂t²+ω²₀ϕ = 0 ∂²x/∂t²+ω²₀x = 0 Powyższe równanie nazywamy równaniem ruchu harmonicznego prostego.

Wahadło matematyczne - punkt materialny o masie m zawieszony na nierozciągliwej i nieważkiej nici o długości l. W rzeczywistości każde wahadło musi być zbudowane w ten sposób, że nić jest nieco rozciągliwa i posiada pewną masę, a kulka metalowa zawieszona na tej nici jest większa od punktu matematycznego. Siła kierująca k jest stosunkiem siły F = mgsinα do wychylenia, które w przybliżeniu wynosi x, wtedy związek k = mgsinα/x, a dla małych wychyleń (sinα ≈ α) zachodzi k = mg/l. Podstawiając do równania: T=2Π pierwiastek z (m/k) otrzymujemy T=2Π pierwiastek z (l/g) Wprowadzając do równania T = 2Π√(I₀/md²)/mgd wyrazimy okres wahadła fizycznego wzorem: T=2Π pierwiastek z (l/g) Jeśli wahadło zamocujemy w ten sposób, że będzie mogło wahać się wokół osi przechodzącej przez środek wahań, to okres wyrazi się wzorem: T' = 2Π√(I₀/md'²)/md. Długość zredukowana będzie wyrażona wzorem: I' = d'+I₀/md, Okres natomiast wzorem: T' = 2Π√(l'/g). Okresy T i T' są sobie równe, co udowodnimy poniżej. W tym celu zauważmy, że zachodzi związek l - d = d'. Różnicę l - d z tego równania można porównać z różnicą obliczoną ze wzoru l = d+(I₀/md), gdzie l-d = (I₀/md). Stąd otrzymujemy I₀/md' = d. Podstawiając tę wielkość do równania l' = d'+I₀/md,otrzymamy l' = d'+d, stąd po podstawieniu pod d' wartości z równania l-d = d' wynika związek l = l'. Równość długości zredukowanych oznacza również równość okresów T =T'. Zatem okres oscylacji wahadła fizycznego wokół osi przechodzącej przez punkt O jest taki sam jak okres oscylacji wokół osi równoległej przechodzącej przez środek wahań O'. Za pomocą tego zjawiska można wyznaczyć wykorzystując wahadło rewersyjne przyspieszenie ziemskie. Krótka charakterystyka pola grawitacyjnego. Dla ciał, których rozmiary są bardzo małe w stosunku do ich wzajemnej odległości, siła oddziałująca na nie jest odwrotnie proporcjonalna do iloczynu tych mas. Można to zapisać:F ~ m₁'m₂'/r² . Masa grawitacyjna charakteryzuje zdolność do oddziaływania grawitacyjnego z innymi ciałem. Ponieważ masa ta jest zawsze proporcjonalna do masy bezwładnej, to mówimy masa ciała i siłę grawitacyjną możemy zapisać w postaci: F = G(m₁m₂/r²) , gdzie G jest współczynnikiem proporcjonalności zwanym stałą grawitacji. Stała G jest równa sile, z jaką przyciągają się dwa punkty materialne o masie 1 kg każdy z odległości 1 m, a jej wartość wynosi: G = 6,67 *10^-17 Nm²kg^-2 .Natężenie pola grawitacyjnego - jest to stosunek siły grawitacyjnej F przez ciało (źródło pola) o masie M i działającej na inne ciało o masie m umieszczone w polu: γ = F/m Natężenie pola grawitacyjnego jest liczbowo równe sile działającej w danym punkcie pola na umieszczone w nim ciało o masie jednostkowej. Natężenie pola grawitacyjnego jest wektorem, który ma kierunek, zwrot wektora siły grawitacji wywieranej przez źródło pola. Jednostką natężenia pola w układzie SI jest 1 N/kg. γ = F/m = (GMm/R²)/m = GM/R² Zatem natężenie w danym punkcie pola nie zależy od masy ciała w nim umieszczonego, lecz tylko od masy ciała wytwarzającego pole i od odległości tego punktu, od źródła pola. Tak więc natężenie pola charakteryzuje samo pole, a nie ciała w nim umieszczone. Stosując druga zasadę dynamiki do siły ciężkości, otrzymamy: F = mg gdzie F - ciężar ciała tj. siła ciążenia ciała ku Ziemi, g - przyspieszenie ziemskie. Z wzoru γ = F/m wynika, że natężenie pola grawitacyjnego jest równoznaczne z przyspieszeniem, z jakim poruszałaby się masa, gdyby znalazła się w danym punkcie pola. Natężenie pola grawitacyjnego jest wielkością wektorową.

Potencjał grawitacyjny - to stosunek energii potencjalnej ciała umieszczonego w danym punkcie pola grawitacyjnego do masy tego ciała. V = Ep/m Jednostką potencjału grawitacyjnego w układzie SI jest 1 J/kg, a jego wymiarem [V] = J/kg = (kgm²/s²)kg = m²/s². Wiedząc, że wartość wykonanej pracy jest równa zmianie energii potencjalnej, można zapisać: W =  Ep ⇒ W = Ep₂ -Ep_1, gdzie Ep2 i Ep1 to wartości energii potencjalnych posiadanych przez ciało o masie m w punktach początkowym i końcowym. Posługując się równaniem V = Ep/m wartości tych energii można zapisać: Ep = mV ⇒ Ep₁ = mV₁ i Ep₂ = mV₂, gdzie V1, V2 to odpowiednio potencjały pola grawitacyjnego w punktach początkowym i końcowym. Tak więc praca związana z przeniesieniem ciał w polu grawitacyjnym między dwoma punktami dowolnie wybranymi może być wyrażona równaniem: W = Ep₂-Ep₁ ⇒ W = mV₂-mV₁ ⇒ W = m(V₂-V₁). Energia potencjalna w danym punkcie pola grawitacyjnego jest równa pracy jaką siły zewnętrzne muszą wykonać równoważąc siłę grawitacji przy przeniesieniu ciała z odległości nieskończenie dużych na odległość r. Porównując i przekształcając wymienione równania możemy ustalić od czego on zależy W = GMm(1/R₁-1/R₂), W = m(GM/R₁ -GM/R₂) V₁-V₂ = -(GM/R₂-GM/R₁), Tak więc potencjał pola można wyrazić równaniem: V =-GM/R.Z powyższego równania wynika, iż potencjał w danym punkcie pola grawitacyjnego zależy od masy źródła pola i odległości rozważanego punktu od tego źródła. Promieniotwórczość naturalna sprowadza się do przemian zachodzących w jądrach pierwiastków ciężkich, począwszy od Z=81 do Z=92. Zmiany zachodzące w jądrach pierwiastków promieniotwórczych naturalnych dzielimy na przemiany α , β i γ.Przemiana β wiąże się z emisją elektronu i protonu. Emisja cząstek β powiększa dodatni ładunek jądra o jednostkę (liczba atomowa Z rośnie o jeden) nie zmieniając liczby masowej. A zatem wskutek przemiany β jądro danego pierwiastka przekształca się w jądro pierwiastka przesuniętego o jedno miejsce naprzód w układzie Mendelejewa.

Zapis rozpadu β^-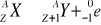

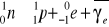
n - neutron, p. - proton, e - elektron, γ_e - antyneutrino elektronowe

Zasięg cząstek β^- można wyznaczyć przy przejściu cząstki przez absorbent o określonej grubości. Jeśli między źródłem cząstek β^- , a detektorem umieścimy absorbent o zmiennej grubości, to liczba cząstek przenikających przez absorbent maleje wraz ze wzrostem grubości absorbentu, dla R_max g/cm² 0,02 < R < 0,3, E_β-_max MeV E=1,92⋅R^0,725, można wyznaczyć jedynie tzw. zasięg efektywny, czyli grubość absorbentu przez który przenika mała część cząstek. Cząstka naładowana, przechodząc przez materię oddziałuje z atomami ośrodka, przy czym oddziaływanie to może być sprężyste bądź niesprężyste. Cząstka naładowana może oddziaływać z elektronami atomu lub z jądrem co może prowadzić do reakcji jądrowych lub rozproszenia potencjalnego. Jednak prawdopodobieństwo zajścia reakcji jądrowej jest znikome. Przy rozproszeniu niesprężystym zostaje wyemitowany foton i w ten sposób zostaje wyemitowane promieniowanie hamujące.W przypadku zderzenia cząstki z elektronem z powłoki atomowej możliwe jest wywołanie jonizacji lub wzbudzenia atomu. Prawdopodobieństwo zajścia obu tych procesów jest bardzo zbliżone oraz przez wzgląd na to, że oba procesy dominują, promieniowanie hamowania można pominąć. Jonizacją właściwą nazywamy liczbę par jonów wytworzonych przez cząstkę naładowaną na jednostkowej drodze w danym ośrodku. Zależy ona od rodzaju cząstki i ośrodka oraz od energii cząstki.

Zdolność hamowania ośrodka równa jest liczbowo stracie energii cząstki na jednostkowej drodze. Jest ona wprost proporcjonalna do jonizacji właściwej, a dla danego ośrodka jest tym większa im większy jest ładunek cząstki i im mniejsza jest jej prędkość.Podczas zderzenia występują znaczne zmiany kierunku prędkości elektronów, przy jednoczesnej małej zmianie wartości prędkości. Tory elektronów są bardzo złożone i rzeczywista droga elektronów jest wielokrotnie większa od grubości absorbentu. Tak więc strumień elektronów poruszających się w danym kierunku zostaje zmniejszony przez ich zahamowanie i wychwycenie przez atomy oraz w wyniku zmiany kierunku prędkości. Istnieje maksymalna grubość absorbentu, przez który mogą przejść elektrony. Jest to zasięg maksymalny i odpowiada cząstkom o maksymalnej energii. Na podstawie badań zależności zasięgu maksymalnego R_max od energii maksymalnej E_βmax uzyskano szereg empirycznych zależności pozwalających oszacować R_max na podstawie znajomości E _βmax i odwrotnie.

Liczbę elektronów wytrącanych ze strumienia I w cienkiej warstwie absorbentu o grubości dx można wyrazić równaniem: dI=μIdx, gdzie μ-jest liniowym współczynnikiem osłabienia. Wartość współczynnika μ jest wprost proporcjonalna do grubości absorbentu. W związku z tym wielkość μ=μ/ρ, zwana masowym współczynnikiem osłabienia, zmienia się bardzo wolno. Dla różnych ośrodków współczynnik absorbcji jest prawie stały, co sprawia, że dla różnych ośrodków część strumienia elektronów ulegających absorbcji i rozproszeniu jest prawie jednakowa. dI=μIdx, gdzie μ=μ/ρ - jest masowym współczynnikiem osłabienia [cm/g] dx=dxρ - jest grubością absorbentu [g/cm] Po scałkowaniu powyższego równania otrzymujemy zależność: I=I₀e^-μx , gdzie I₀- jest strumieniem elektronów dochodzących do absorbentu.Zdolność absorbcyjną ośrodka określa się często podając tzw. Grubość połówkowego osłabienia x_1/2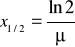
Jeżeli strumień cząstek β wysyłany jest w półpełny kąt bryłowy to współczynnik absorbcji μ związany jest z E _βmax (górną granicą energii widma β^-.)przybliżoną zależnością: μ=0.0155(E _βmax)^-1.44. Aby wyznaczyć maksymalną energię cząstek β^- należy dokonać pomiaru liczby cząstek, które docierają do detektora po przejściu przez absorbent o grubości x [mg/cm] przy ustalonym czasie rejestracji Δt. IΔt=I_oΔt e^-μx N=IΔt - liczba cząstek zarejestrowana w czasie przy x≠0 N_o=IoΔt - liczba cząstek zarejestrowana w czasie przy x=0 Równanie to możemy zapisać inaczej: N=N₀ e^-μx Wykonując pomiary zależności liczby cząstek N od grubości absorbentu x możemy wyznaczyć parametry tej prostej. ln N_t=lnN₀-μR_max

---
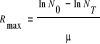
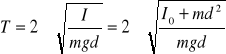