AKADEMIA BYDGOSKA

im. Kazimierza Wielkiego

Wydział Matematyki ,Techniki i Nauk Przyrodniczych

LABORATORIUM FIZYKI

Temat: Wyznaczanie współczynnika sztywności na

skręcanie metodą statyczną.

Wykonali:

Marcin Lewandowski

Bartosz Karczewski

BYDGOSZCZ 2003

Spis treści:

1. Część teoretyczna . . . . . . . . . . . . . . . . . . . . . . . . . . str.3

2. Przebieg ćwiczenia . . . . . . . . . . . . . . . . . . . . . . . . . . str. 4

3. Ocena błędów . . . . . . . . . . . . . . . . . . . . . . . . . . . . str. 6

1. Część teoretyczna.

Deformacja albo sprężyste odkształcenia ciał wywołane działaniem sił zewnętrznych mogą przejawiać się w różnych postaciach, np. wydłużenia, skręcania.

Z najprostszym przykładem skręcania spotykamy się wówczas, gdy na element objętościowy sprężystego ciała stałego ( którego przekrój jest prostokątem ) o umocowanej podstawie działa siła F przyłożona do górnej powierzchni S tegoż elementu i do niej równoległa. Nastąpi wtedy sprężyste odkształcenie postaci, którego miarą będzie kąt zsunięcia płaszczyzn bocznych α. Zgodnie z prawem Hooke'a ciśnienie jest proporcjonalne do odkształcenia, a więc:

(1)

gdzie: τ - oznacza współczynnik stały dla danego materiału, zwany modułem sztywności na skręcanie albo modułem skręcania. Jednostka modułu sztywności, zgodnie z powyższym określeniem, jest taka sama jak jednostka ciśnienie, tj.
lub
.

2. Przebieg ćwiczenia.

Zestaw urządzeń do przeprowadzenia ćwiczenia:

• przyrząd pomiarowy,

• odważniki,

• mikromierz.

Pręt zamocowany na jednym końcu poddany jest działaniu znanego momentu skręcającego. Wyznaczamy kąt skręcania ϕ, po czym obliczamy wartość momentu kierującego zgodnie ze wzorem:

(2)

Po wykonaniu pomiarów kąta skręcania dla różnych obciążeń szalki (np. 10 obciążeń szalki wartościami 20 - 100g) mierzymy trzykrotnie średnicę krążka 2R, pamiętając o konieczności uwzględnienia głębokości rowka, w którym znajduje się struna. Obliczamy moment skręcający:

(3)

oraz moment kierujący D dla każdego obciążenia osobno, po czym obliczamy średnią wartość momentu kierującego D_śr. Znajdujemy średnicę badanego pręta 2r. Mierzymy ją śrubą mikrometryczną 3 razy.

Długość pręta l mierzymy miarką milimetrową (3 pomiary). Współczynnik sztywności obliczamy ze wzoru:

(4)

Wyniki pomiarów i obliczeń:

Obciążenie szalki F [N]	Kat skręcenia ϕ			M [N]	D [N]	τ [N/m^2] x 10^11
		Na lewo	Na prawo				Średni
50g	20°	20°	20°	0,1	0,286	1,64
100g	38°	38°	38°	0,2	0,3	1,72
150g	40°	40°	40°	0,3	0,43	2,46
250g	43°	43°	43°	0,5	0,66	3,78
300g	45°	45°	45°	0,6	0,76	4,35
Średnia średnica pręta				2 x 10^-3 m
Średnia długość pręta				0,9 m
Średnia średnica krążka				0,2 m
Średni współczynnik sztywności na skręcanie				2,79 x 10^11 [N/m^2]

Wartość średnia współczynnika sztywności na skręcanie τ_śr.

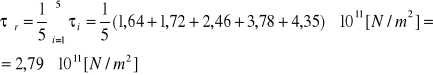
Błąd bezwzględny pomiaru:

Błąd względny pomiaru:

3. Ocena błędów.

Błąd pomiaru średnicy pręta Δ r wynosi ±0,1 mm, ponieważ taka jest dokładność suwmiarki, którą była mierzona średnica pręta.

Błąd pomiaru długości pręta Δ l i krążka ΔR wynosi ±0,5 mm - dokładność przymiaru kreskowego.

5

---