Ćwiczenie nr 10

Obliczanie współczynnika refrakcji atmosferycznej

1. Sprzęt

Kalkulator, tablice fizyczne - prężność pary nasyconej w powietrzu, papier kancelaryjny, papier milimetrowy A-4

2. Miejsce odbywania ćwiczeń

Sala III G w budynku Geodezji.

3. Cel ćwiczeń

Określenie zmienności współczynnika refrakcji atmosferycznej dla fal optycznych i radiowych, dla zadanych warunków atmosferycznych

4. Opis zagadnienia

Prędkość rozchodzenia się fal elektromagnetycznych w próżni jest dla całego widma promieniowania elektromagnetycznego jednakowa i stanowi uniwersalną stałą fizyczną c. Aktualnie obowiązująca w geodezji wartość liczbowa stałej c została zalecona przez Międzynarodową Asocjacje Geodezyjną i wynosi:

c= 299 792 458±1,2 m/s

Prędkość rozchodzenia się fali w danym ośrodku określa się wzorem

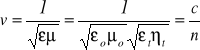
gdzie:

ε_o, μ_{o -} przenikalność elektryczna i magnetyczna próżni

ε_t, μ_t - względne przenikalności ośrodka

c - prędkość fali elektromagnetycznej w próżni

n - współczynnik refrakcji atmosfery

Prędkość rozchodzenia się fal elektromagnetycznych w powietrzu zależy głównie od trzech parametrów meteorologicznych: t, p, e ośrodka oraz od długości λ fali nośnej. Zależność ta wyraża się ogólnie poprzez współczynnik załamania (refrakcji)

Prędkość danej fali monochromatycznej jest identyfikowana z prędkością rozchodzenia się fazy i dlatego nazywana jest prędkością fazowa ν_ϕ.

Sygnał pomiarowy wytworzony poprzez modulacją fali nośnej stanowi grupę fal monochromatycznych rozchodzącymi się w powietrzu z różnymi prędkościami fazowymi, natomiast ten sam sygnał rozchodzi się w tymże ośrodku z prędkością grupowa v_g. Wielkości tej nie można utożsamiać ze średnią prędkością fazową dla całej grupy fal. Zjawisko to zwane jest dyspersja, a ośrodek w którym ono zachodzi - ośrodkiem dyspersyjnym.

Związek między prędkością grupowa a prędkością fazową określony jest wzorem Raylei

wyrażenie
reprezentuje charakterystykę dyspersyjna danego ośrodka i wyraża zależność funkcjonalną prędkości v_ϕ od długości λ_v fali nośnej. Dla próżni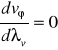
, w związku, z czym v_g=v_ϕ=c. Z pojęciem prędkości fazowej i grupowej wiążą się pojęcia fazowego współczynnika załamania n_ϕ oraz grupowego współczynnika załamania n_g. Ta ostatnią wielkość wyraża się wzorem

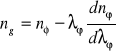
Dla próżni n_g = n_ϕ =1 Zależność fazowego współczynnika załamania od długości fali wyraża się wzorem Cauchy'ego

Jak widzimy, dwa ostatnie człony prawej strony wzoru mogą mieć istotne znaczenie tylko dla małych wartości λ_v. W praktyce, jako wielkość graniczną przyjmuje się λ_v=1 cm, powyżej której zjawisko dyspersji nie wywiera istotnego wpływu na wartość v. W związku z tym grupowy współczynnik załamania wyznacza się tylko w przypadku stosowania fali lub grupy fal o długościach λ_v≤ l cm, a więc dla milimetrowych fal radiowych i dla fal z zakresu optycznego. Natomiast dla mikrofal o długościach λ_v> l cm wpływ dyspersji jest praktycznie niewyczuwalny i z tego względu dla tego zakresu przyjmuje się v_g=v_ϕ. W związku z powyższym do wyznaczania fazowego i grupowego współczynnika załamania stosuje się odrębne wzory matematyczne.

Współczynnik refrakcji mikrofal

W zakresie mikrofalowym, z wyjątkiem częstotliwości bliskich 60 i 22 GHz, współczynnik refrakcji atmosferycznej nie zależy od długości fali, a jedynie od temperatury, ciśnienia i wilgotności atmosfery. Zależność tę opisują empiryczne wzory Essena,. Smitha-Weintrauba oraz Essena-Frooma. Międzynarodowa Unia Geodezji i Geofizyki IUGG zaleciła w 1960 r. zastosowanie wzoru Essena-Frooma. Ma on postać:

n= 1+N x 10^-6 - współczynnik refrakcji

T - temperatura powietrza w°K

P - ciśnienie atmosferyczne w hPa

e - cząstkowa prężność pary wodnej hPa

Jest stosowany wzór równoważny

gdzie p i e wyrażone są w mm Hg.

Prężność pary wodnej e jest określana w praktyce pomiarowej poprzez pomiar temperatury suchego t i zwilżonego t^', termometru w psychrometrze aspiracyjnym

gdzie:

t i t^' - temperatura suchego i zwilżonego termometru w °C

e^' - prężność pary nasyconej w temperaturze t^' (z tablic)

p, e - w jednakowych jednostkach

Współczynnik refrakcji fal optycznych

Podobnie jak dla mikrofal MUGG zaleciła stosowanie współczynników Barella i Searsa. Dla suchego powietrza o temperaturze 0°C, ciśnieniu 760 mm Hg

λ - wyrażono w μm.

Dla dowolnych warunków meteorologicznych współczynnik refrakcji według wzoru Barrela i Searsa ma postać:

gdzie T wyrażono w °K, e i p w hPa

Jest stosowany wzór równoważny

gdzie T wyrażono w °K, e i p w mm Hg

Tablice do określenia prężności nasyconej pary wodnej w zależności od temperatury ^oC w hPa

Prężność nasyconej pary wodnej w zależności od temperatury ^oC w hPa
0	1	2	3	4	5	6	7	8	9	10
6,09007	6,55158	7,04102	7,56105	8,11433	8,70219	9,32729	9,99229	10,69985	11,44997	12,24797
10	11	12	13	14	15	16	17	18	19	20
12,24797	13,09252	13,98894	14,93723	15,94271	17,00804	18,13322	19,32490	20,58441	21,91441	23,32155
20	21	22	23	24	25	26	27	28	29	30
23,32155	24,80450	26,36991	28,02044	29,76141	31,59548	33,52797	35,56287	37,70417	39,95719	42,32592

Opracowano na podstawie:

Jerzy Szymoński - Instrumentoznawstwo geodezyjne

Krzysztof Holejko- Precyzyjne elektroniczne pomiary odległości i kątów

---