Tomasz Sewruk 151345

Zadanie1:

2) "Miejsca zerowe"

Dana jest funkcja f(x)=x2-4x sin(x)+4 sin2(x), dla której zachodzi f(P)=0, P=(-1,3). Wyznacz ręcznie pierwsze trzy przybliżenia miejsca zerowego P1,P2,P3 metodą Newtona startując z obu krańców przedzialu. Następnie wyznacz miejsca zerowe funkcji z dokładnością δ=0.001 używając odpowiedniego skryptu Octava (Matlaba). Porównaj wynik iteracji z metodą punktu stalego. Skomentuj liczbę potrzebnych iteracji dla każdego z podanych punktów startowych. Zaproponuj nowy punkt startowy P0 tak, aby wyznaczyć miejsce zerowe w P=0. Używając komeny plot zrób wykres funkcji f(x) na zadanym przedziale oraz zaznacz na nim ręcznie graficzną interpretację metody Newtona i punktu stałego. Wydruk wykresu (wraz z kodem) dołącz do sprawozdania.

Student: Tomasz Sewruk SR TN 9.15

Postać funkcji:

Postać pochodnej funkcji:

Wyznaczenie trzech pierwszych przybliżeń miejsca zerowego:

Zaczynam z lewej strony przedziału w poszukiwaniu pierwszego miejsca zerowego:

Sprawdzenie:

Sprawdzenie:

Sprawdzenie:

Widać że pierwszym miejscem zerowym jest wartość: 0

Zaczynam z prawej strony przedziału:

Sprawdzenie:

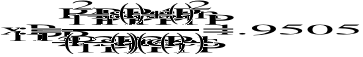
Sprawdzenie:

Sprawdzenie:

Widać że drugim miejscem zerowym jest wartość: 1.895

Przyjąłem przy obliczeniach dokładność: 0.001

Zatem wynika że miejscem zerowym wyżej napisanej funkcji f(x) jest wartość: 0 i 1.895

Wykres funkcji f(x): (wynik uzyskany z programy Mathcad)

Kod z Matlaba dla Nowego Punktu startowego który wynosi: -1

>> xpom=linspace(-1,3);

>> p0=-1; delta=0.001; tol=0.001; max1=20;

>> [k, p, err, P, GP] = newton('f','df', p0, delta, tol, max1)

k =

10

p =

1.9059

err =

0.0102

P =

-1.0000

3.2364

2.6637

2.3496

2.1571

2.0405

1.9730

1.9358

1.9161

1.9059

GP =

0.4664

11.7350

3.0413

0.8577

0.2411

0.0661

0.0176

0.0046

0.0012

0.0003

>> p0=-1; tol=0.001; max1=20;

>> [k,p,err,P] = fixpt('g',p0,tol,max1)

k =

7

p =

2.6990e-008

err =

1.8179e-004

P =

-1.0000

0.7305

0.4109

0.1353

0.0149

0.0002

0.0000

>> ypom=sqrt(4*xpom.*sin(xpom)-4*sin(xpom).*sin(xpom)); %postać funkcji w pliku g

>> y=(-2)*(xpom-2*sin(xpom)).*(2*cos(xpom)-1); %pochodna z pliku df

>> funkcja=xpom.^2-4*xpom.*sin(xpom)+4*sin(xpom).*sin(xpom); %postać funkcji z pliku f

>> plot(xpom,y,'r-',xpom,ypom,'k-',xpom,funkcja,'b');

>> grid on

>> legend('pochodna df(x)','met.punktu stalego','funkcja f(x)');

Wynik iteracji dla metody Newtona jest wartość 10 a dla metody Punktu Stałego wartość ta wynosi 7, zatem wynika z tego iż metoda Newtona jest metodą mniej dokładną

Kod z Matlaba dla Nowego Punktu startowego który wynosi: -0,5

>> xpom=linspace(-1,3);

>> p0=-0.5; delta=0.001; tol=0.001; max1=20;

>> [k, p, err, P, GP] = newton('f','df', p0, delta, tol, max1)

k =

5

p =

-0.0237

err =

0.0238

P =

-0.5000

-0.1962

-0.0955

-0.0475

-0.0237

GP =

0.2105

0.0375

0.0091

0.0022

0.0006

>> p0=-0.5; tol=0.001; max1=20;

>> [k,p,err,P] = fixpt('g',p0,tol,max1)

k =

5

p =

5.7622e-007

err =

8.3950e-004

P =

-0.5000

0.1986

0.0321

0.0008

0.0000

>> ypom=sqrt(4*xpom.*sin(xpom)-4*sin(xpom).*sin(xpom)); %postać funkcji w pliku g

>> y=(-2)*(xpom-2*sin(xpom)).*(2*cos(xpom)-1); %pochodna z pliku df

>> funkcja=xpom.^2-4*xpom.*sin(xpom)+4*sin(xpom).*sin(xpom); %postać funkcji z pliku f

>> plot(xpom,y,'r-',xpom,ypom,'k-',xpom,funkcja,'b');

>> grid on

>> legend('pochodna df(x)','met.punktu stalego','funkcja f(x)');

Jak widać z przeprowadzonej symulacji wynik iteracji dla metody Newtona wynosi wartość 5, dla metody Punktu Stałego wartość ta wynosi 5, więc tyle samo jednak gdy spojrzeć na wartość błędu bezwzględnego można wyciągnąć wniosek że metoda punktu stałego jest metodą bardziej dokładną.

Wnioski końcowe:

Z wyników powyżej wnioskuję że obie metody są dobre jeśli nie zależy nam na ilości iteracji i dokładności gdyż wynik wyjdzie podobny. Jednak gdy się temu bardziej przyjrzeć to metoda Newtona jest metodą gorszą od od metody Punktu Stałego ze względu na wynik uzyskanych iteracji (powtórzeń) oraz na wynik błędu bezwzględnego. Zauważyć można również że jeśli wybieramy punkt startowy bliżej miejsca zerowego tym ten błąd jest mniejszy jeśli chodzi o metodę Punktu Stałego. Natomiast w metodzie Newtona jest odwrotnie, im dalej od miejsca zerowego tym mniejszy błąd popełnimy.

---