Politechnika Śląska w Gliwicach
Wydział Elektryczny
semestr II ; grupa I
WYZNACZANIE WSPÓŁCZYNNIKA PRZEWODNICTWA CIEPLNEGO METALI METODĄ ANGSTRÖMA
sekcja 4 :
Paweł Rothkegel
Rafał Sitkiewicz
Michał Marzec
1. WSTĘP TEORETYCZNY
Wymiana ciepła pomiędzy dwoma ciałami o różnych temperaturach może przebiegać na trzy sposoby:
promieniowanie,
unoszenie (konwekcja),
przewodnictwo.
Podstawą samego zjawiska przewodnictwa cieplnego jest przekazywanie energii kinetycznej chaotycznego ruchu cieplnego drobin Jest ono jednym z tzw. zjawisk transportu. Prawo przewodnictwa cieplnego sformułował J.B. Fourier w roku 1822. Wykazał on, że gęstość strumienia cieplnego q jest proporcjonalna do gradientu temperatury:
gdzie:
- współczynnik przewodnictwa cieplnego
Znak minus w prawie Fouriera oznacza, że energia w procesie przewodnictwa cieplnego przenosi się w kierunku zmniejszania temperatury. Powyższy związek jest słuszny jednie pod warunkiem, że względna różnica temperatur na odległości średniej drogi swobodnej cząsteczek jest mała w porównaniu z jednością:
W razie niespełnienia powyższego warunku związek pomiędzy gradientem temperatury i gęstością strumienia cieplnego staje się bardziej skomplikowany.
Proces przewodnictwa cieplnego w ciałach stałych, a co za tym idzie w metalach, związany jest z drganiami sieci krystalicznej i zależy od jej struktury. Według kwantowej teorii ciał stałych drgania termiczne sieci krystalicznej są skończonym zbiorem drgań normalnych tworzących w procesie interferencji paczki falowe zwane fononami. W metalach na sieciowe przewodnictwo cieplne nakłada się zjawisko z ruchem elektronów pasma przewodnictwa. Dla temperatur wyższych od temperatury Debye'a (np. w warunkach pokojowych) przewodnictwo cieplne elektronowe związane jest z przewodnością elektryczną σ prawem Wiedemanna-Franza:
gdzie:
k - stała Boltzmanna
e - ładunek elektronu
Niech w pręcie o długości L wytworzona będzie stała różnica temperatur T=T1-T2. Równanie przewodnictwa cieplnego zapiszemy wówczas w postaci :
gdzie:
κ - współczynnik przewodnictwa temperaturowego
Założeniem jest, że wymiana ciepła pomiędzy prętem i ośrodkiem podlega prawu Newtona a parametry κ i wynoszą odpowiednio:
![]()
Angström podał następujące warunki brzegowe rozwiązania powyższego równania:
na jednym końcu pręta (x=0) temperatura zmienia się okresowo i można wyrazić ją za pomocą szeregu Fouriera:
gdzie:
n - indeks n-tej harmonicznej
temperatura drugiego końca pręta (x=L) jest stała, równa temperaturze wody chłodzącej.
W odległości x od źródła ciepła temperatura pręta opisana jest ogólnym równaniem:
Po przeprowadzeniu obliczeń dokładnie przedstawionych w skrypcie otrzymamy wzór wskazujący okresowe zmiany temperatury, podobny nieco do równania fali (stąd pojęcie tzw. fal temperaturowych). Zakładamy, że jeśli dla punktu x=1 temperatury będą zmieniać się w sposób zbliżony do sinusoidalnych to możemy przyjąć n=1. Wówczas dla składowej rzeczywistej otrzymamy:
T1=Ae-ax cos(t-bx)
i analogicznie dla punktu przesuniętego o l:
T1=Ae-a(x+l) cos[t-b(x+l)]
Stosunek kolejnych fal temperaturowych pozwala wyliczyć współczynnik a:
a z przesunięcia fazowego wyliczamy współczynnik b:
gdzie:
- okres zmian warunków grzania
t - czasowe przesunięcie grzbietów fal
Stąd ostatecznie otrzymujemy wzór na współczynnik przewodnictwa temperaturowego w metalowym pręcie:
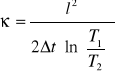
2. PRZEBIEG ĆWICZENIA
1. Włączamy obieg wody chłodzącej.
2. Za pomocą autotransformatora ustalamy napięcie zasilające grzejnik na 80 [V].
3. Uruchamiamy program angstrem.bat.
4. Po nagrzaniu grzejnika nakładamy go na „ciepły” koniec badanego pręta i równocześnie rozpoczynamy rejestrację pomiarów. Wytwarzamy w pręcie okresowe zmiany temperatury poprzez nakładanie i zdejmowanie grzejnika. Czas grzania i chłodzenia przyjmujemy np. 5 min.
okresowe zmiany temperatury nakładając i zdejmując grzejnik. Czas grzania i chłodzenia przyjmujemy równy 5 minut.
5. Pomiary kończymy po wytworzeniu 3 - 5 cykli grzewczo - chłodzących.
6. Dane pomiarowe zapisane są w pliku pomiary.dat w 9 kolumnach zawierających, czas, temperaturę i błąd jej pomiaru dla kolejnych punktów pomiarowych.
Za pomocą odpowiedniego programu komputerowego rysujemy wykresy czasowych zmian temperatury poszczególnych punktów pręta.
8. Określamy przesunięcie czasowe fal temperaturowych Δt oraz ich amplitudy w poszczególnych punktach pręta oddalonych od siebie o Δl = 10 cm.
9. obliczamy współczynnik przewodnictwa temperaturowego stosując dane dla kolejnych par punktów pomiarowych pręta.
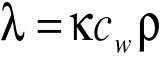
10. obliczamy średnią wartość współczynnika temperaturowego a następnie współczynnik przewodnictwa cieplnego według wzoru:
gdzie:
cw - ciepło właściwe pręta
ρ - gęstość materiału pręta
3. WYNIKI POMIARÓW I OBLICZENIA
Wyniki przeprowadzonych pomiarów znajdują się na dyskietce. Wykres czasowych zmian temperatury poszczególnych punktów pręta znajduje się na stronie 9.
Pręt wykonany jest z miedzi, dla której ciepło właściwe wynosi 0,4•103 [ J / kg K ], natomiast gęstość materiału pręta jest równa 8,9•103 [ kg / m3 ].
Pomiary i wykresy fal temperaturowych rejestrowanych przez termistory 3 i 4 odrzucamy w obliczeniach, gdyż nie mają charakteru sinusoidalnego.
Przewodnictwo temperaturowe liczymy na podstawie amplitud fal i czasowego przesunięcia ich grzbietów w dwóch olejnych maksimach z wykresów dla termistora 1 i 2 korzystając z wzoru:
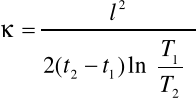
Natomiast błąd liczymy metodą różniczki zupełnej:
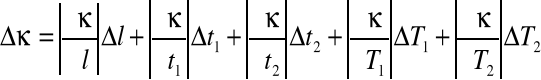
Gdzie:
l - odległość między 2 punktami pomiarowymi [m]
t1 - czas osiągnięcia temperatury maksymalnej 1 punktu pomiarowego w określonym cyklu grzewczo - chłodzącym [s]
t2 - czas osiągnięcia temperatury maksymalnej 2 punktu pomiarowego w określonym cyklu grzewczo - chłodzącym [s]
T1 - wartość temperatury maksymalnej 1 punktu pomiarowego w określonym cyklu grzewczo - chłodzącym [K]
T2 - wartość temperatury maksymalnej 2 punktu pomiarowego w określonym cyklu grzewczo - chłodzącym [K]
Korzystając z wyników przeprowadzonych przez komputer otrzymujemy następujące dane:
dla pierwszego cyklu:
T1= 326,26 ΔT1= 0,14 t1 = 319,11 Δt1 = 0,01
T2= 307,41 ΔT2= 0,14 t2= 489,11 Δt2= 0,01
dla drugiego cyklu:
T1= 340,06 ΔT1= 0,15 t1 = 916,15 Δt1 = 0,01
T2= 316,43 ΔT2= 0,19 t2= 1043,09 Δt2= 0,01
dla trzeciego cyklu:
T1= 346,98 ΔT1= 0,48 t1 = 1515,06 Δt1 = 0,01
T2= 321,78 ΔT2= 0,45 t2= 1600,09 Δt2= 0,01
dla czwartego cyklu:
T1= 350,48 ΔT1= 0,15 t1 = 2115,07 Δt1 = 0,01
T2= 325,07 ΔT2= 0,15 t2= 2206,08 Δt2= 0,01
Natomiast l = 0,1 Δl = 0,01
Korzystając z programu mathcad otrzymujemy następujące wyniki:
κ1 = 0,0005 Δκ1 = 0,0001
κ2 = 0,0005 Δκ2 = 0,0001
κ3 = 0,0008 Δκ1 = 0,0002
κ4 = 0,0007 Δκ2 = 0,0002
κśr = 0,00064 Δκśr = 0,00013
zatem κ = (6,4![]()
1,3)![]()
10-4
Korzystając ze wzoru
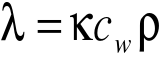
obliczamy współczynnik przewodnictwa cieplnego
λ![]()
=2172,5 [ J m-1 s-1 K-1] ]
Błąd natomiast obliczamy ze wzoru:
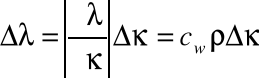
Δλ = 441,3 a zatem
λ=(2,1![]()
0,45) ![]()
10-3 [ J m-1 s-1 K-1] ]
4.Wnioski
Na znaczny błąd badanej wielkości składają się przede wszystkim źle dobrane czasy osiągania maksimów temperaturowych a także same wartości temperatur maksymalnych. Wielkości te odczytane są przez komputer z dużym błędem. Nie mają wiec charakteru sinusoidalnie zmiennego a zatem nie są zgodne z założeniami ANGSTRÖMA.
1
![]()
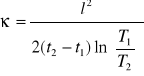
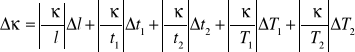
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
metoda Bragga, Księgozbiór, Studia, Fizyka
Metoda Angstoma, Księgozbiór, Studia, Fizyka
Ladunek wlasciwy-metoda magnetronowa, Księgozbiór, Studia, Fizyka
metoda Bragga, Księgozbiór, Studia, Fizyka
06 Badanie zaleznosci sily, Księgozbiór, Studia, Fizyka
Kopia cechowanie termopary, Księgozbiór, Studia, Fizyka, Biofizyka
modułu sztywności metodą dynamiczną, Budownictwo-studia, fizyka
Drgania har. -Aga, Księgozbiór, Studia, Fizyka
Wyznaczanie energii maksymalnej promieniowania beta, Księgozbiór, Studia, Fizyka
IS1, Księgozbiór, Studia, Fizyka
Analiza spr, Księgozbiór, Studia, Fizyka
LABFIZ08, Księgozbiór, Studia, Fizyka
bragg, Księgozbiór, Studia, Fizyka
więcej podobnych podstron