Politechnika Śląska w Gliwicach

Wydział Elektryczny

Kierunek : Elektronika i Telekomunikacja

Studia inżynierskie

Wyznaczanie ładunku właściwego e/m metodą magnetronową.

Wykonali:

Rafał Szczęsny

Daniel Sekuła

1.Wstęp teoretyczny

Ładunek elementarny wyznaczył R.A. Millikan. Oto opis prowadzonego przez niego doświadczenia:

- do wnętrza płaskiego kondensatora wprowadza się rozpylone kropelki oleju. Opadanie kropelki oświetlonej światłem bocznym obserwuje się za pomocą lunetki z okularem metrycznym. Znając prędkość opadania oraz dane materiałowe ośrodka i oleju można wyznaczyć promień kropli. Następnie kroplę jonizujemy stosując preparat promieniotwórczy. Znając prędkość przemieszczania się naładowanej kropli w obecności pola elektrycznego wewnątrz kondensatora można wyznaczyć wartość ładunku. Millikan wykazał, że ładunek kropli jest całkowitą wielokrotnością ładunku elementarnego e = 1.6 * 10 C.

Magnetron jest lampą nadawczą dużej mocy sygnałów wielkiej częstotliwości, np. mikrofal. Na ćwiczeniu wykorzystujemy efekt magnetronowy realizowany przez diodę umieszczoną w podłużnym polu magnetycznym.

Zjawiska występujące podczas poruszania się ładunku w polu magnetycznym.

Pomiędzy cylindrycznymi okładkami diody prostowniczej występuje niejednorodne pole elektryczne o natężeniu:

gdzie:

U_a - napięcie anodowe

r_a ,r_k - promienie anody i katody

Jeśli lampę umieścimy współosiowo wewnątrz cewki to pole magnetyczne będzie miało kierunek prostopadły do kierunku elektronów emitowanych z katody i podążających do dodatniej anody.Ze strony pól elektrycznego i magnetycznego na poruszający się ładunek działa siła Lorentza:

Pod wpływem tej siły tor elektronu ulegnie zakrzywieniu, zmieni się pęd a promień krzywizny obliczymy porównując siłę Lorentza z siłą odśrodkową:

Krzywoliniowe tory elektronów nazywają się kardioidami, przypominające cykloidy (pokazane na poniższych rysunkach ).

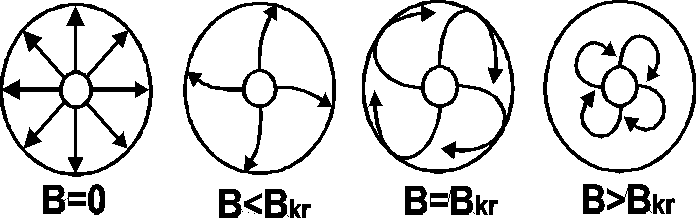
Jeśli przez cewkę nie płynie prąd, to indukcja magnetyczna B=0 i elektrony biegną promieniście do anody. Ze wzrostem wartości indukcji magnetycznej elektrony poruszają się po spiralach o coraz mniejszym promieniu krzywizny.Przy pewnej, odpowiednio dużej, indukcji magnetycznej tory elektronów nie osiągają anody i natężenie prądu anodowego zaczyna się stopniowo zmniejszać.

Teoretycznie dla B=B_k powinniśmy obserwować zanik prądu anodowego. Elektrony termoemisji posiadają różne prędkości, a więc w sytuacji krytycznej tylko część elektronów będzie zawracać w kierunku katody, a elektrony wolniejsze będą po torach rozwijających się spiral docierać do anody.

W dowolnym punkcie toru elektron posiada moment pędu względem osi elektrod :

gdzie:

r - odległość od osi

Pod działaniem sił pól elektrycznego i magnetycznego zmienia się pęd. Moment sił wywołuje zmianę momentu pędu. Całkując równanie dL = eBrdr otrzymamy moment pędu elektronu w punkcie zetknięcia elektronu z anodą:

.

Zakładając, że w warunkach „krytycznych” krzywizna toru wynosi r_a/2, a tor jest styczny do powierzchni anody, otrzymamy:

Prędkość elektronu w momencie zetknięcia z anodą obliczymy stosując zasadę zachowania energii:

skąd

Po ostatecznych przekształceniach otrzymamy:

,

gdzie :

B_kr - indukcja magnetyczna, przy której elektrony nie dolatują do anody

Indukcja magnetyczna w środku długiego solenoidu określona jest wzorem :

B = μ_oIn

gdzie:

- przenikalność magnetyczna próżni ,

I_n- natężenie płynącego prądu ,

n- liczba zwojów przypadająca na jednostkę długości cewki .

Gdy zależność między indukcją magnetyczną a natężeniem prądu wyrazimy wzorem empirycznym :

B = μ₀βI

gdzie:

- współczynnik zależny od geometrii cewki , liczby warstw , liczby zwojów w warstwie . W przypadku cewki stosowanej w zestawie β = 5.3 ⋅10³ m^-1.

wtedy ładunek właściwy e/m możemy obliczyć ze wzoru :

gdzie :

r_a = (2,00 ± 0,05)mm - promień anody

r_k = (1,00 ± 0,02)mm - promień katody

2. Przebieg ćwiczenia.

1. Łączymy obwód wg. schematu z instrukcji.

2. Przy ustalonym napięciu anodowym notujemy zmiany natężenia prądu anodowego i_a spowodowane zmianą natężenia prądu płynącego przez solenoid I . Natężenie prądu I zmieniamy w granicach 0 ÷ 1500 mA co 100 mA .

3. Wykonujemy pomiary dla trzech różnych wartościach napięcia anodowego:

4. Tabela pomiarowa

I	Prąd anodowy Ia [mA] dla:
[mA]	Ua1=6,3[V]	Ua2=8,07[V]	Ua3=10,15[V]
30	22,6	32,25	44
110	22,6	32,25	44
200	22,6	32,2	43,75
310	22	31,5	43
398	21,7	31	42,5
500	21,4	30,6	42
600	20,8	30	41,25
710	18,5	28,5	39,5
800	13,6	23,2	35,5
900	9,8	16,5	26,25
1000	7,4	12	19
1100	6	9,5	15
1200	4,8	7,5	12
1300	3,94	6,25	10
1410	3,1	5	8
1500	2,6	4,25	6,5

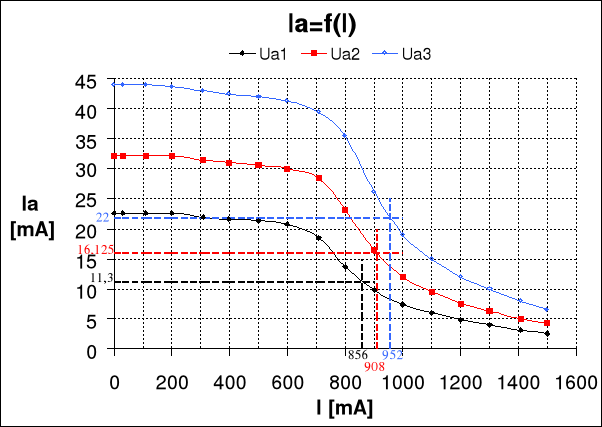
5. Rysujemy rodziny charakterystyk I_a = f(I).

6. Z wykresów odczytujemy wartości krytyczne ( ) prądu płynącego przez solenoid odpowiadające dwukrotnemu spadkowi prądu anodowego ( w porównaniu z wartością początkową przy I = 0 ).

Dla U_a1 - I_kr1 = 0.856 A

Dla U_a2 - I_kr2 = 0.908 A

Dla U_a3 - I_kr3 = 0.952 A

7. Obliczamy ładunek właściwy e/m według wzoru :

Obliczenie jednostki ładunku właściwego elektronu:

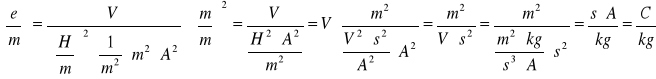
Dla U_a1 = 6.3 V :

e₁/m = U_a * 200,3899*10¹⁰ /I_kr² = 1,72 * 10¹¹ [C/kg]

Dla U_a2 = 8.07 V :

e₂/m. = 1,96 *10 ¹¹ [C/kg]

Dla U_a3 = 10.15 V :

e₃/m. = 2,24 *10¹¹ [C/kg]

8. Przeprowadzamy rachunek błędów:

DANE WYKORZYSTYWANYCH MIERNIKÓW

Miernik	Klasa [%]	Zakres	Δx
Woltomierz	0,2	15 [V]	0,03 [V]
Miliamperomierz Ia	0,2	75 [mA]	0,15 [mA]
Miliamperomierz Im	0,2	1500 [mA]	3 [mA]

Obliczamy błąd wielkości złożonej metodą różniczki zupełnej według wzoru:

.

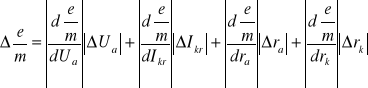
Δe/m = 0,27 * 10¹¹ [C/kg]

Δe/m = 0,18 * 10¹¹ [C/kg]

Δe/m = 0,22 * 10¹¹ [C/kg]

Zatem :

e₁/m = (1,72 ± 0,27)*10¹¹ [C/kg]

e₂/m = (1,96 ± 0,18)*10¹¹ [C/kg]

e₃/m = (2,24 ± 0,22)*10¹¹ [C/kg]

Za pomocą średniej ważonej wyznaczamy ostateczną wartość ładunku właściwego e/m.

gdzie :

Do obliczeń przyjmujemy c = 10²²

Lp.	xi*10^11 [C/kg]	Δxi*10^11 [C/kg]	wi	wixi*10^11 [C/kg]	wiΔxi*10^11 [C/kg]
1	1,72	0,27	13,72	23,59	3,7
2	1,96	0,18	30,86	60,49	5,55
3	2,24	0,22	20,66	46,28	4,54
Suma			65,24	130,36	13,79

Błąd maksymalny średniej ważonej:

otrzymujemy: Δ(e/m) = 0,1057*10¹¹ [C/kg]

Po obliczeniach i zaokrągleniu uzyskanego wyniku otrzymujemy: e/m = (1,99 ± 0,11) ∗ 10¹¹ [C/kg]

3.Wnioski.

Porównując wynik końcowy z wartością tablicową (e/m = 1.7588 × 10¹¹ C/kg) można powiedzieć że metoda magnetronowa do wyznaczenia ładunku właściwego e/m, daje wynik rożniący się o około 13,6 %. Zastosowanie dokładniejszych przyrządów pomiarowych pozwoliłoby prawdopodobnie zbliżyć się do wartości tablicowej.

Semestr II

Grupa II

Sekcja III

---