Badanie zależności między cechami
Badanie zbiorowości ze względu na dwie cechy ma zazwyczaj na celu poszukiwanie zależności między tymi cechami. Poszukiwanie to ma sens tylko wtedy, gdy między cechami może istnieć logicznie uzasadniony związek przyczynowo-skutkowy lub związek o charakterze współzależności. Analizując związek przyczynowo - skutkowy między cechami ustalamy, która z badanych cech może być traktowana jako cecha niezależna, a którą uznamy za cechę zależną, np. badając wpływ stażu pracy (X) na wysokość wynagrodzenia (Y) przyjmiemy, że cechą niezależną będzie staż pracy (X) zaś wynagrodzenie będzie cechą zależną. W niektórych przypadkach można stwierdzić zarówno wpływ cechy X na cechę Y jak i odwrotnie. Mówimy wówczas o współzależności cech, np. stopa procentowa i inflacja, kurs walutowy i inflacja.
Zależność między cechami może mieć charakter:
funkcyjny - polegający na tym, że każdej wartości zmiennej X odpowiada ściśle określona i tylko jedna wartość zmiennej Y. Przykładem może być tu zależność między ceną a wartością towaru.
stochastyczny - wpływ jednej zmiennej na drugą jest zależny również od czynników losowych, wspólnie działających na obie zmienne, oprócz innych czynników działających na każdą z nich oddzielnie.
Szczególnym przypadkiem zależności stochastycznej jest zależność statystyczna (korelacyjna) występująca między cechami mierzalnymi lub quasi-mierzalnymi. Polega ona na tym, że wartościom jednej zmiennej przyporządkowane są określone średnie wartości drugiej zmiennej.
Pod względem kierunku wyróżniamy korelację dodatnią i ujemną.
Korelacja dodatnia występuje wtedy, gdy wzrostowi wartości jednej cechy odpowiada wzrost średnich wartości drugiej cechy (lub spadkowi wartości jednej cechy odpowiada spadek średnich wartości drugiej cechy).
Korelacja ujemna występuje wtedy, gdy wzrostowi wartości jednej cechy odpowiada spadek średnich wartości drugiej cechy.
W sytuacjach badania zbiorowości statystycznej jednocześnie ze względu na dwie cechy X i Y zachodzi konieczność porządkowania danych z uwzględnieniem wariantów każdej z tych cech.. Dane dotyczące dwóch cech przedstawiane są w dwojaki sposób:
w szeregu szczegółowym złożonym z par wariantów lub wartości (xi, yi) cech X i Y dla każdej jednostki statystycznej, (stosowanym dla małych zbiorowości),
w tablicy korelacyjnej/kontyngencji.
Analiza korelacji
Aby uzyskać wstępną ocenę istnienia zależności korelacyjnej między cechami możemy posłużyć się:
- uporządkowanymi szeregami statystycznymi, tzn. jeśli wartości cech w obu porównywanych szeregach mają tendencję wzrostową, to możemy oczekiwać istnienia korelacji dodatniej, natomiast jeśli wzrostowi wartości jednej cechy odpowiada tendencja spadkowa w drugim szeregu, wskazuje to na istnienie korelacji ujemnej.
- korelacyjnym wykresem rozrzutu - na płaszczyźnie zaznaczamy punkty (xi, yi) o współrzędnych odpowiadających wartościom obu cech, otrzymujemy w ten sposób diagram korelacyjny. Punkty tego diagramu mogą układać się wzdłuż pewnej linii. Gdy jest to prosta będąca wykresem rosnącej (malejącej) funkcji liniowej - mówimy o dodatniej (ujemnej) korelacji liniowej. Gdy punkty diagramu układają się wzdłuż pewnej krzywej, mamy do czynienia z korelacją krzywoliniową. Brak regularności w ułożeniu punktów lub ich ułożenie wzdłuż prostej równoległej do osi Ox wskazuje na brak związku korelacyjnego.
Współczynnik korelacji liniowej Pearsona
Jeśli wstępna analiza pozwoli na stwierdzenie istnienia korelacyjnej zależności prostoliniowej między cechami, to do oceny siły tego związku najczęściej stosowanym miernikiem jest współczynnik korelacji liniowej Pearsona. Współczynnik ten można wyznaczać tylko w przypadku, gdy obie cechy są mierzalne.
Współczynnik korelacji Pearsona obliczamy stosując następujący wzór dla szeregu szczegółowego:
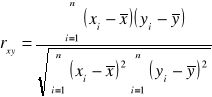
Jeśli chcemy określić tylko kierunek korelacji, możemy wyznaczyć kowariancję, którą dla szeregu szczegółowego wyznacza się z następującego wzoru:
![]()
Ujemna kowariancja, a zatem ujemny współczynnik korelacji wskazują na istnienie ujemnej, a dodatnia - na istnienie dodatniej korelacji między cechami. Jeśli znamy wartość kowariancji i odchylenia standardowe każdej z cech, możemy obliczyć wartość współczynnika korelacji Pearsona ze związku:
![]()
.
Współczynnik korelacji Pearsona ma następujące własności:
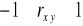
.Im większa jest wartość bezwzględna współczynnika
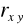
, tym silniejsza jest zależność między cechami. Umownie przyjmuje się, że gdy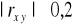
to nie ma zależności liniowej między cechami.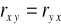
zatem współczynnik korelacji nie wskazuje, która cecha jest od której zależna.
Współczynnik korelacji rang Spearmana
Innym miernikiem siły i kierunku zależności korelacyjnej między cechami jest współczynnik korelacji rang Spearmana (współczynnik zgodności uporządkowania). Może być on stosowany :
tylko dla danych uporządkowanych w szeregu szczegółowym,
dla cech mierzalnych lub quasi-mierzalnych (jakościowych, dających się uporządkować).
Aby wyznaczyć wartość współczynnika korelacji rang, poszczególnym wartościom każdej z cech nadajemy rangi w następujący sposób:
1) Wartości lub warianty każdej z cech porządkujemy rosnąco lub malejąco (przyjmując takie samo kryteriów porządkowania dla obu cech),
2) Jednostkom w każdym z uporządkowań nadajemy liczbę odpowiadającą ich miejscu w tym uporządkowaniu a w sytuacji, gdy wystąpią jednakowe wartości dla kilku jednostek - średnią arytmetyczną takich miejsc. Tak ustalone (oddzielnie dla każdej cechy) liczby nazywamy rangami.
Współczynnik korelacji rang określa wzór:
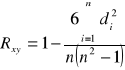
,
w którym di jest różnicą między rangami odpowiadających sobie wartości xi cechy X i wartości yi cechy Y.
Współczynnik Spearmana posiada takie same własności jak współczynnik Pearsona.
Finanse i rachunkowość 2012/2013 opracowanie: SAN, Katedra
Statystyki i Ekonometrii
1
Wyszukiwarka
Podobne podstrony:
FiR wykład 1, FiR SAN Łódź, semestr 3, Statystyka
Testy dla dwoch srednich, FiR SAN Łódź, semestr 3, Statystyka
ANALIZA DYNAMIKI, FiR SAN Łódź, semestr 3, Statystyka
tablice rozkladow, FiR SAN Łódź, semestr 3, Statystyka
Wzory statystyczne FiR 2012, FiR SAN Łódź, semestr 3, Statystyka
Obszary krytyczne II, FiR SAN Łódź, semestr 3, Statystyka
Stat FiR TEORIA II (miary cd, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Rynki finansowe - wykłady (2009) - II wersja, FIR UE Katowice, SEMESTR IV, Rynki finansowe, Rynki fi
rynki walutowe b puszer 734, FIR UE Katowice, SEMESTR IV, Rynki Walutowe, Rynki walutowe - część I,
Wykład 3, FIR UE Katowice, SEMESTR IV, Finanse przedsiębiorstw, fp, Finanse przedsiębiostwa - wszyst
QUIZ statystyczny statystyka opisowa (DS), FiR, licencjat, semestr 2, Statystyka
test 20sprawozdawczość1, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR V, Sprawozdawczość fin
Stat FiR TEORIA III (estymacja, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Wykład 10, FIR UE Katowice, SEMESTR IV, Finanse przedsiębiorstw, fp, Finanse przedsiębiostwa - wszys
TI pytania sem1.13r, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR II, Technologia Informatyc
TI EGZAMIN PRZEPISANE - z odpowiedziami, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR II, Te
egzamin makro, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR II, Makroekonomia, Wykłady - Chu
Finanse - wykład, FiR UG LSN, 5 semestr, Finanse samorządu terytorialnego, Finanse samorządu terytor
więcej podobnych podstron