STATYSTYKA
I ANALIZA STRUKTURY
Pojęcia wstępne
Statystyka jest nauką o metodach badania zjawisk masowych, służącą ich poznaniu poprzez wykrycie prawidłowości i zasadniczych tendencji rządzących tymi zjawiskami.
Badanie statystyczne (w naukach społecznych) - ogół prac mających na celu poznanie struktury zbiorowości, ocenę współzależności między cechami, ocenę zmian zjawiska w czasie.
Etapy badania statystycznego:
- projektowanie badania (określenie celu badania, charakteru badania, sposobu pozyskania danych, przygotowanie materiałów do przeprowadzenia badania),
- gromadzenie materiału statystycznego i jego opracowanie (grupowanie i prezentacja),
- analiza wyników obserwacji.
Zbiorowość (populacja) statystyczna - zbiór jednostek (osób, przedmiotów lub zjawisk) poddanych badaniu statystycznemu. Zbiorowość (populację) generalną tworzą wszystkie jednostki, w stosunku do których formułowane są wnioski ogólne z badania. Aby określić, zgodnie z celem badania zbiorowość generalną należy wszystkie jednostki określić pod względem rzeczowym (co lub kogo badamy), przestrzennym (jaki obszar obejmuje badanie), czasowym (jaki okres obejmuje badanie lub w jakim momencie się odbywa). W zależności od tego, jak liczna jest zbiorowość statystyczna oraz jakie są możliwości (czasowe, finansowe) badacza, a zatem jak pełna jest obserwacja statystyczna, prowadzone mogą być 2 typy badań. Badanie statystyczne pełne (całkowite) to takie, w którym bezpośredniej obserwacji statystycznej podlegają wszystkie elementy populacji generalnej. Jeśli bezpośredniej obserwacji podlega tylko pewien podzbiór populacji generalnej, tzw. próba, to badanie nazywamy częściowym. Badania tego typu prowadzi się szczególnie wtedy, gdy zbiorowość jest bardzo liczna i objęcie badaniem wszystkich jej elementów byłoby zbyt pracochłonne i kosztowne lub w wyniku obserwacji jednostki statystyczne mogłyby ulec zniszczeniu.
W zależności od celu badania wyróżnia się pewne istotne właściwości jednostek statystycznych - cechy statystyczne (np. płeć, wzrost, waga, wiek). Rozróżnia się dwa typy cech statystycznych: jakościowe i ilościowe. Cechy jakościowe (niemierzalne: porządkowe, nominalne) to takie, których warianty ustala się w sposób opisowy, np. płeć, wykształcenie … Z kolei, warianty cech ilościowych (mierzalnych: skokowych, ciągłych) wyrażone są za pomocą liczb w określonych jednostkach miary, np. wzrost (w cm), waga (w kg), wiek (w latach).
Szereg statystyczny - uporządkowany szereg liczbowy pod względem określonych kryteriów, tzn. szeregiem statystycznym jest szereg liczb zawierający dane dotyczące jednej zbiorowości i jednej cechy.
Źródła pozyskiwania danych:
pierwotne (obserwacja, wywiad, ankieta),
wtórne (sprawozdawczość, publikacje statystyczne).
Rodzaje szeregów:
szczegółowy
![]()
rozdzielczy = rozkład empiryczny
punktowy
z przedziałami klasowymi
klasyczne (średnia arytmetyczna, średnia harmoniczna, średnia geometryczna),
pozycyjne.
jest wielkością mianowaną,
spełnia warunek:
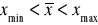
,jest wielkością teoretyczną, tzn. istnieje możliwość, że
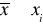
,suma odchyleń od średniej wynosi zero, tzn.
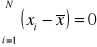
,nie można obliczyć dla przedziałów otwartych,
jest wrażliwa na skrajne wartości (obserwacje przypadkowe).
kwantyle (kwartyle, decyle),
dominanta.
dla szeregu szczegółowego:
dla szeregu rozdzielczego:
jest wielkością mianowaną,
nie zależy od wartości skrajnych,
można ją obliczyć dla szeregów z przedziałami otwartymi,
jest wielkością przybliżoną, jej dokładność zależy od wielkości przedziałów klasowych.
|
|
|
|
. . . |
. . . |
|
|
|
|
|
|
. . . |
. . . |
|
|
- rozróżnienie pomiędzy przedziałami zamkniętymi i otwartymi,
- ustalanie granic przedziałów w zależności od tego, czy cechy są skokowe czy ciągłe. ![]()
lub ![]()
gdzie: ![]()
- rozpiętość przedziału klasowego i,
![]()
- górna granica przedziału i,
![]()
- dolna granica przedziału i.
Wskaźnik struktury (częstość, frakcja, odsetek) - występowania danego wariantu cechy - stosunek liczby jednostek o danym wariancie cechy do liczebności badanej zbiorowości:

,
![]()
, ![]()
![]()
lub ![]()
.
gdzie: ![]()
- liczba jednostek o i-tym wariancie cechy (liczebność przedziału i),
![]()
- liczba wariantów cechy (liczba przedziałów klasowych),
![]()
- liczebność zbiorowości.
Wskaźnik podobieństwa struktur
![]()
,
![]()
gdzie: ![]()
- wskaźniki struktury dla pierwszej zbiorowości,
![]()
- wskaźniki struktury dla drugiej zbiorowości.
MIARY POŁOŻENIA :
Miary położenia (miary przeciętne) - informują o przeciętnym poziomie wartości rozważanej cechy w badanej zbiorowości statystycznej:
Średnie klasyczne - opierają się na wszystkich obserwacjach, ich obliczanie nie jest trudne i nie wymaga porządkowania danych.
Średnia arytmetyczna - suma wartości cechy mierzalnej podzielona przez liczebność zbiorowości.
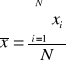
- dla szeregu szczegółowego,
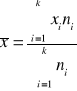
- dla szeregu rozdzielczego punktowego,
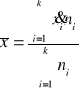
- dla szeregu rozdzielczego z przedziałami klasowymi,
Własności średniej arytmetycznej:
Pozycyjne miary położenia - wyznaczane są na podstawie szeregu uporządkowanego; należą do nich:
Dominanta (modalna, moda, wartość najczęstsza) - wartość cechy statystycznej, która w danym rozkładzie empirycznym występuje najczęściej.
- w szeregu rozdzielczym punktowym jest to ta wartość cechy, której odpowiada największa liczebność,
- w szeregu rozdzielczym z przedziałami klasowymi stosujemy wzór interpolacyjny:
![]()
x0 - dolna granica przedziału dominanty (przedziału wartości, któremu odpowiada największa
liczebność),
n0 - liczebność przedziału dominanty,
n-1 - liczebność przedziału poprzedzającego przedział dominanty,
n+1 - liczebność przedziału następnego po przedziale dominanty,
h0 - rozpiętość przedziału dominanty (i jemu sąsiadujących przedziałów).
Własności dominanty:
1. Jej wyznaczenie ma sens tylko, jeśli rozkład jest jednomodalny (występuje jedno max),
2. Przedział dominanty i przedziały sąsiednie muszą mieć taką samą rozpiętość,
3. Nie da się jej wyznaczyć, gdy liczebność największa jest w przedziale skrajnym lub w sąsiedztwie przedziałów otwartych.
Mediana- dzieli zbiorowość na dwie równe części, tzn. połowa jednostek ma wartości cechy mniejsze lub równe medianie, a druga połowa wartości cechy równe lub większe od mediany,
![]()
![]()
- dla szeregu o nieparzystej liczbie jednostek,
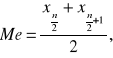
![]()
- dla szeregu o parzystej liczbie jednostek.
![]()
![]()
gdzie: ![]()
- wartość dolnej granicy przedziału mediany,
![]()
- rozpiętość przedziału mediany,
![]()
- liczebność przedziału mediany,
![]()
- numer mediany,
![]()
- wartość skumulowana poprzedzająca przedział mediany.
Własności mediany:
Finanse i rachunkowość 2012/2013 opracowanie: Joanna Trębska
Wyszukiwarka
Podobne podstrony:
Fir wyklad 7, FiR SAN Łódź, semestr 3, Statystyka
Testy dla dwoch srednich, FiR SAN Łódź, semestr 3, Statystyka
ANALIZA DYNAMIKI, FiR SAN Łódź, semestr 3, Statystyka
tablice rozkladow, FiR SAN Łódź, semestr 3, Statystyka
Wzory statystyczne FiR 2012, FiR SAN Łódź, semestr 3, Statystyka
Obszary krytyczne II, FiR SAN Łódź, semestr 3, Statystyka
Stat FiR TEORIA II (miary cd, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Rynki finansowe - wykłady (2009) - II wersja, FIR UE Katowice, SEMESTR IV, Rynki finansowe, Rynki fi
rynki walutowe b puszer 734, FIR UE Katowice, SEMESTR IV, Rynki Walutowe, Rynki walutowe - część I,
Wykład 3, FIR UE Katowice, SEMESTR IV, Finanse przedsiębiorstw, fp, Finanse przedsiębiostwa - wszyst
QUIZ statystyczny statystyka opisowa (DS), FiR, licencjat, semestr 2, Statystyka
test 20sprawozdawczość1, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR V, Sprawozdawczość fin
Stat FiR TEORIA III (estymacja, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Wykład 10, FIR UE Katowice, SEMESTR IV, Finanse przedsiębiorstw, fp, Finanse przedsiębiostwa - wszys
TI pytania sem1.13r, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR II, Technologia Informatyc
TI EGZAMIN PRZEPISANE - z odpowiedziami, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR II, Te
egzamin makro, UE KATOWICE - FIR - Rachunkowość, I stopień, SEMESTR II, Makroekonomia, Wykłady - Chu
Finanse - wykład, FiR UG LSN, 5 semestr, Finanse samorządu terytorialnego, Finanse samorządu terytor
więcej podobnych podstron