Stat FiR TEORIA III (estymacja, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW

Pytania z teorii

Statystyka

Podstawy wnioskowania, dobór próby, rozkłady statystyk z próby

Co rozumiemy pod pojęciem wnioskowania statystycznego?
Wyjaśnij pojęcie populacji generalnej i populacji próbnej. Podaj przykłady.
Wyjaśnij pojęcie próby prostej.
Wyjaśnij pojęcie losowania indywidualnego, nieograniczonego i niezależnego.
Wyjaśnij pojęcie próby reprezentatywnej.
Wymień etapy badania statystycznego.
Wyjaśnij pojęcia losowania niezależnego i losowania zależnego. Podaj przykłady takich losowań.
Na czym polega losowanie warstwowe? Podaj przykład takiego losowania.
Na czym polega losowanie zespołowe? Podaj przykład takiego losowania.
Na czym polega losowanie systematyczne? Podaj przykład takiego losowania.
Wyjaśnij pojęcie operatu losowania i podaj dwa przykłady takich operatów.
Wymień trzy metody nielosowego doboru próby i wyjaśnij jedną z nich.
Co rozumiemy pod pojęciem statystyki próby? Podaj dowolny przykład takiej statystyki wraz z interpretacją.
Przedstaw i scharakteryzuj dowolny przykład rozkładu statystyki z próby.
Naszkicuj funkcję gęstości rozkładu t-Studenta i podaj, ile wynoszą parametry w tym rozkładzie.
Naszkicuj funkcję gęstości rozkładu chi-kwadrat i podaj, ile wynoszą parametry w tym rozkładzie.
Naszkicuj funkcję gęstości rozkładu F-Fischera-Snedecora i podaj, ile wynoszą parametry w tym rozkładzie.

Metody estymacji

Wyjaśnij pojęcia estymacji i weryfikacji.
Co rozumiemy pod pojęciem estymatora? Podaj przykład.
Co rozumiemy pod pojęciem oceny parametru? Wyjaśnij na przykładzie.
Co rozumiemy pod pojęciem estymatora punktowego, a co pod pojęciem estymatora przedziałowego? Wyjaśnienie poprzyj przykładem.
Wyjaśnij pojęcie estymacji punktowej. Podaj stosowny przykład.
Wyjaśnij pojęcie estymacji przedziałowej. Podaj stosowny przykład.
Omów i wyjaśnij własność nieobciążoności estymatora.
Omów i wyjaśnij własność zgodności estymatora.
Omów i wyjaśnij własność efektywności estymatora.
Podaj estymator punktowy średniej populacji. Wyjaśnij zastosowane oznaczenia.
Podaj estymator punktowy wariancji populacji. Wyjaśnij zastosowane oznaczenia.
Podaj estymator punktowy wskaźnika struktury populacji. Wyjaśnij zastosowane oznaczenia.
Co to jest błąd standardowy średniej? Podaj wzór i wyjaśnij zastosowane oznaczenia.
Co to jest błąd standardowy wskaźnika struktury? Podaj wzór i wyjaśnij zastosowane oznaczenia.
Wyjaśnij pojęcie przedziału ufności. Wyjaśnienie poprzyj przykładem.
Co rozumiemy pod pojęciem poziomu ufności. Wyjaśnienie poprzyj przykładem.
Podaj wzór pozwalający oszacować przedziałowo średnią populacji w przypadku, gdy rozkład badanej zmiennej jest normalny. Wyjaśnij zastosowane oznaczenia. Przy jakich założeniach można stosować ten wzór?
Podaj wzór pozwalający oszacować przedziałowo średnią populacji w przypadku, gdy nie jest znany rozkład badanej zmiennej. Wyjaśnij zastosowane oznaczenia. Przy jakich założeniach można stosować ten wzór?
Podaj wzór pozwalający oszacować przedziałowo wariancję populacji. Wyjaśnij zastosowane oznaczenia. Przy jakich założeniach można stosować ten wzór?
Podaj wzór pozwalający oszacować przedziałowo odchylenie standardowe populacji. Wyjaśnij zastosowane oznaczenia. Przy jakich założeniach można stosować ten wzór?
Podaj wzór pozwalający oszacować przedziałowo wskaźnik struktury populacji. Wyjaśnij zastosowane oznaczenia. Przy jakich założeniach można stosować ten wzór?
Co oznacza
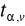
? Wyjaśnienie zobrazuj rysunkiem.
Co oznacza
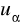
? Wyjaśnienie zobrazuj rysunkiem.
Co oznacza
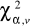
? Wyjaśnienie zobrazuj rysunkiem.
Wyjaśnij pojęcia wiarygodności oraz dokładności estymacji przedziałowej. Jaki jest między nimi związek?
W jaki sposób liczebność próby wpływa na dokładność estymacji przedziałowej? Wyjaśnienie zobrazuj przykładem.
W jaki sposób zróżnicowanie próby wpływa na dokładność estymacji przedziałowej? Wyjaśnienie zobrazuj przykładem.
W jaki sposób poziom ufności wpływa na dokładność estymacji przedziałowej? Wyjaśnienie zobrazuj przykładem.
Wymień trzy czynniki wpływające na długość przedziału ufności.
Co rozumiesz pod pojęciem minimalnej liczebności próby?
Podaj wzory (i wyjaśnij, kiedy każdy z nich jest stosowany) na minimalną liczebność próby przy szacowaniu średniej populacji. Wyjaśnij zastosowane oznaczenia.
Podaj wzory (i wyjaśnij, kiedy każdy z nich jest stosowany) na minimalną liczebność próby przy szacowaniu wskaźnika struktury populacji. Wyjaśnij zastosowane oznaczenia.

Testowanie hipotez

Co rozumiemy pod pojęciem hipotezy statystycznej? Podaj przykład takiej hipotezy.
Co rozumiemy pod pojęciem hipotezy parametrycznej? Podaj przykład takiej hipotezy.
Co rozumiemy pod pojęciem hipotezy nieparametrycznej? Podaj przykład takiej hipotezy.
Co to jest hipoteza zerowa oraz hipoteza alternatywna? Wyjaśnienie poprzyj przykładem.
Wyjaśnij pojęcia hipotezy dwustronnej i jednostronnej (prawo- oraz lewostronnej).
Co to jest błąd I rodzaju? Wyjaśnienie poprzyj przykładem.
Co to jest błąd II rodzaju? Wyjaśnienie poprzyj przykładem.
Wyjaśnij związek między prawdopodobieństwem popełnienia błędu I rodzaju a prawdopodobieństwem popełnienia błędu II rodzaju.
Co to jest moc testu?
Co to jest poziom istotności testu?
Co to jest obszar krytyczny testu? Wyjaśnienie zobrazuj rysunkiem.
Co to jest dwustronny obszar krytyczny i w jakich sytuacjach jest stosowany?
Co to jest prawostronny obszar krytyczny i w jakiej sytuacjach jest stosowany?
Co to jest lewostronny obszar krytyczny i w jakiej sytuacjach jest stosowany?
Na czym polega proces weryfikacji hipotez? (krótko scharakteryzuj)
Do czego służy test t-Studenta?
Do czego służy test U?
Do czego służy test chi-kwadrat?
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o średniej populacji (gdy rozkład populacji jest normalny). Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o średniej populacji (gdy nie jest znany rozkład populacji). Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o wariancji populacji. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o odchyleniu standardowym populacji. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o wskaźniku struktury populacji. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o równości średnich dwóch populacji (gdy rozkłady obu populacji są normalne). Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o równości średnich dwóch populacji (gdy rozkłady populacji są nieznane). Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o równości wariancji dwóch populacji. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o równości odchyleń standardowych dwóch populacji. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez, wzór funkcji testowej i warunki stosowalności testu w przypadku testowania hipotezy o równości wskaźników struktury dwóch populacji. Wyjaśnij wprowadzone oznaczenia.
Wyjaśnij pojęcie krytycznego poziomu istotności. Wyjaśnienie zobrazuj rysunkiem.
Wyjaśnij związek między estymacją parametrów populacji generalnej a testowaniem hipotez dotyczących tych parametrów. Wyjaśnienie poprzyj przykładem.

Korelacja i regresja (część 1 - statystyka opisowa)

Wyjaśnij pojęcia analizy korelacji i analizy regresji.
Wyjaśnij pojęcia siły, kierunku i kształtu zależności między dwiema cechami.
Wyjaśnij pojęcia korelacji dodatniej i korelacji ujemnej. Podaj przykłady obu korelacji.
Wyjaśnij pojęcie diagramu korelacyjnego. Podaj przykład.
Wyjaśnij pojęcie tablicy korelacyjnej, rozkładów brzegowych i rozkładów warunkowych. Podaj wzory pozwalające wyznaczyć parametry obu rozkładów brzegowych (średnie arytmetyczne i odchylenia standardowe).
Podaj wzór na współczynnik korelacji liniowej Pearsona. Wyjaśnij wprowadzone oznaczenia. Kiedy można stosować tę miarę korelacji? Jak interpretuje się jej wartość?
Podaj wzór na współczynnik korelacji rang Spearman'a. Wyjaśnij wprowadzone oznaczenia. Kiedy można stosować tę miarę korelacji? Jak interpretuje się jej wartość?
Wyjaśnij pojecie rangowania oraz pojęcie „rang wiązanych” przy wyznaczaniu współczynnika korelacji rang Spearmana.
Wyjaśnij pojęcia: regresja prosta, regresja wieloraka, regresja liniowa, regresja krzywoliniowa, zmienna zależna, zmienna niezależna.
Podaj wzór liniowej funkcji regresji w przypadku badania związku dwóch cech (X i Y). Wyjaśnij wprowadzone oznaczenia. Podaj dokładną interpretację parametrów funkcji regresji.
Wyjaśnij pojęcie reszty modelu regresji. Wyjaśnienie zobrazuj rysunkiem.
Wyjaśnij istotę metody najmniejszych kwadratów. W jakim celu stosuje się tę metodę?
Podaj wzory pozwalające wyznaczyć parametry funkcji regresji liniowej (w przypadku badania związku dwóch cech). Wyjaśnij wprowadzone oznaczenia. Przedstaw rysunek obrazujący wartości parametrów a i b.
Przedstaw trzy dowolne miary pozwalające ocenić jakość dopasowania modelu regresji do danych empirycznych. Podaj nazwy tych miar, wzory i wyjaśnij wprowadzone oznaczenia.
Wyjaśnij pojęcie wariancji reszt i odchylenia standardowego reszt. Podaj wzory, wyjaśnij wprowadzone oznaczenia. Jak interpretuje się wartości tych miar?
Podaj wzór na współczynnik determinacji, wyjaśnij wprowadzone oznaczenia. Jak interpretuje się wartość tego współczynnika? Przedstaw związek między współczynnikiem determinacji a współczynnikiem korelacji.
Wyjaśnij sposób wyznaczania statystyki chi-kwadrat w oparciu o tablicę kontyngencji. Podaj wzór na tę statystykę i wyjaśnij wprowadzone oznaczenia.
Podaj wzory na trzy dowolne współczynniki kontyngencji. Podaj nazwy tych współczynników i wyjaśnij wprowadzone oznaczenia. W jakich sytuacjach można stosować te współczynniki? Jak interpretuje się ich wartość?
Wyjaśnij sposób wyznaczania statystyki chi-kwadrat na podstawie tablicy czteropolowej. Podaj wzór na współczynnik Kendalla.

Korelacja i regresja (część 2 - wnioskowanie)

Podaj odpowiedni zestaw hipotez oraz test (wzór funkcji testowej i nazwę testu) służący do sprawdzenia istotności współczynnika korelacji liniowej Pearsona. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez oraz test (wzór funkcji testowej i nazwę testu) służący do sprawdzenia istotności współczynnika korelacji rang Spearman'a. Wyjaśnij wprowadzone oznaczenia.
Podaj odpowiedni zestaw hipotez oraz test (wzór funkcji testowej i nazwę testu) służący do sprawdzenia istotności współczynnika regresji. Wyjaśnij wprowadzone oznaczenia.
Wyjaśnij, w jaki sposób można wnioskować o istotności współczynnika regresji na podstawie przedziału ufności.
Podaj wzór na test niezależności chi-kwadrat. Wyjaśnij wprowadzone oznaczenia. W jakiej sytuacji stosowany jest ten test? Podaj odpowiedni zestaw hipotez.

Pytania zapisane kolorem szarym nie obowiązują do sprawdzianu nr 3. Obowiązują natomiast do „wyjściówki” i egzaminu. Egzamin obejmie również analizę dynamiki (wykład 9)

Na temat doboru próby - pytania 1-12 można przeczytać w:

Wasilewska E.: Statystyka opisowa od podstaw - Rozdział 1.

Na temat korelacji i regresji - pytania 80-98 można przeczytać na str. 273-339 (książka j.w.)