Pytania z teorii
Statystyka
Podstawowe pojęcia
Przedstaw trzy znaczenia słowa statystyka.
Jako zbiór danych liczbowych
Jako wszelkie czynności związane z gromadzeniem i opracowywaniem danych liczbowych
Jako pewne charakterystyki liczbowe
Jako dyscyplina naukowa
Wymień 2 podstawowe działy statystyki (tj. funkcje statystyki jako dyscypliny naukowej).
Statystyka opisowa
Statystyka matematyczna
Co rozumiemy pod pojęciem statystyki opisowej?
Statystyka opisowa - zajmuje się zagadnieniami związanymi z:
-gromadzeniem
-prezentacja
-analizą i interpretacją danych liczbowych
Metody statystyki opisowej wykorzystywane są wtedy, gdy obserwacja statystyczna obejmuje całą badaną zbiorowość.
Co rozumiemy pod pojęciem wnioskowania statystycznego?
Wnioskowanie statystyczne (statystyka matematyczna) zajmuje się uogólnianiem wynikow badania części zbiorowości (tzw. Proby) na całą zbiorowość (tzw. Populację generalną).
Wnioskowanie przebiega ,,od proby do populacji”. Oparte jest ono na zasadach teorii prawdopodobieństwa, przy czym zakłada się, że próba jest pobrana z populacji w sposób losowy.
Co rozumiemy pod pojęciem badania pełnego? Podaj przykład takiego badania.
Badania statystyczne pełne (całkowite, wyczerpujące), - obejmują wszystkie jednostki danej zbiorowości statystycznej. Oznacza to, że każda jednostka zbiorowości poddana jest bezpośredniej obserwacji, tj. informacje zbierane są od wszystkich jednostek zbiorowości. (np. ewidencja urodzeń i zgonów)
Co rozumiemy pod pojęciem badania częściowego? Podaj przykład takiego badania.
Badania częściowe, obejmują niektóre jednostki zbiorowości statystycznej. A więc bezpośredniej obserwacji podlega tylko populacja próbna. (np. badanie odporności samochodów na zderzenia)
Przedstaw przyczyny przeprowadzania badań częściowych.
Niektóre z przyczyn:
Duży koszt badania
Duża czasochlonność badania
Charakter niszczący badania
Wymień etapy badania statystycznego.
PROJEKTOWANIE BADANIA
OBSERWACJA STATYSTYCZNA
OPRACOWANIE MATERIAŁU STATYSTYCZNEGO
ANALIZA STATYSTYCZNA
Co rozumiemy pod pojęciem populacji generalnej? Podaj przykład.
Wyjaśnij pojęcie populacji próbnej. Podaj przykład.
Wyjaśnij pojęcie jednostki statystycznej. Podaj przykład.
Wyjaśnij pojęcie cechy statystycznej. Podaj przykład.
Wyjaśnij pojęcia: cecha statystyczna zmienna, cecha statystyczna stała. Podaj przykłady.
Wymień dwa podstawowe rodzaje cech statystycznych zmiennych. Podaj przykłady takich cech.
Co rozumiemy pod pojęciem cechy niemierzalnej? Podaj przykład takiej cechy.
Co rozumiemy pod pojęciem cechy mierzalnej? Podaj przykład takiej cechy.
Co rozumiemy pod pojęciem cechy ciągłej? Podaj przykład takiej cechy.
Co rozumiemy pod pojęciem cechy skokowej? Podaj przykład takiej cechy.
Co rozumiemy pod pojęciem szeregu szczegółowego? Podaj przykład.
Co rozumiemy pod pojęciem szeregu strukturalnego? Podaj przykład.
Co rozumiemy pod pojęciem szeregu rozdzielczego punktowego? Podaj przykład.
Co rozumiemy pod pojęciem szeregu rozdzielczego przedziałowego? Podaj przykład.
Co rozumiemy pod pojęciem szeregu czasowego? Podaj przykład.
Co rozumiemy pod pojęciem szeregu przestrzennego? Podaj przykład.
Wymień etapy przy konstrukcji szeregu rozdzielczego przedziałowego.
Przedstaw jeden ze sposobów ustalania liczby przedziałów klasowych przy konstrukcji szeregu rozdzielczego. Wyjaśnij na przykładzie.
W jaki sposób wyznacza się rozpiętości przedziałów klasowych konstruując szereg rozdzielczy? Wyjaśnij na przykładzie.
W jaki sposób wyznacza się granice przedziałów klasowych konstruując szereg rozdzielczy? Wyjaśnij na przykładzie.
Wyjaśnij pojęcie szeregu dwuwymiarowego.
Co rozumiemy pod pojęciem liczebności klas? Wyjaśnienie poprzyj przykładem.
Co rozumiemy pod pojęciem liczebności skumulowanej? Podaj przykładową liczebność skumulowaną w zaprezentowanym przez siebie szeregu i zinterpretuj, co dana wielkość oznacza.
Przedstaw i wyjaśnij wzór na wskaźnik struktury. Podaj przykład wskaźnika struktury i zinterpretuj, co dana wielkość oznacza.
Wyjaśnij pojęcie skumulowanego wskaźnika struktury. Podaj przykładowy wskaźnik struktury i zinterpretuj, co dana wielkość oznacza.
Co rozumiemy pod pojęciem gęstości liczebności? Wyjaśnienie poprzyj przykładem.
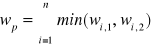
Przedstaw i wyjaśnij wzór na wskaźnik podobieństwa struktur. W jakim celu stosowany jest ten wskaźnik?Zasada wyznaczania wskaźnika podobieństwa struktur jest następująca:
Wyznaczamy wskaźniki struktury w obu szeregach
Dla każdej klasy w szeregu znajdujemy mniejszy z dwóch wskaźników (stąd we wzorze minimum)
Stosujemy te minimalne wskaźniki, otrzymując w ten sposób wartość wp.
Im wartość wp, jest bliższa 1, struktury porównywanych zbiorowości są bardziej podobne
Im wartośc wp bliższa 0, tym struktury są mniej podobne.
Przedstaw interpretację wskaźnika podobieństwa struktur. Podaj przykład.
0-0,2 - podobieństwo bardzo niskie
0,2 - 0,4 - podobieństwo niskie
0,4 - 0,6 - podobieństwo umiarkowane
0,6 - 0,8 - podobieństwo duże
0,8 - 1 - podobieństwo bardzo duże, przy czym jeśli:
Wp = 1 - struktury są identyczne
Rodzaje wykresów statystycznych.
Wykresy punktowe
Wykresy powierzchniowe
Wykresy bryłowe ( trójwwymiarowe, przestrzenne)
Wykresy liniowe
Wykresy obrazkowe
Wykresy mapowe (kartogramy)
Populacja generalna (zbiorowość generalna) - stanowią ją wszystkie elementy będące przedmiotem badania, co do których chcemy formułować wnioski ogólne. Np. Wzrost ludności Polski.
Populacja próbna (zbiorowość próbna) - stanowi ją część elementów wchodzących w skład populacji generalnej. Elementy do próby wybiera się w określony sposób (losowo lub nielosowo). Wzrost mężczyzn, brunetów w ogólnej liczbie mężczyzn..
Jednostka statystyczna - najmniejszy elementy składowy zbiorowości. To wlaśnie jednostka statystyczna jest obiektem bezpośredniej obserwacji. Oznacza to, że wszelkie dane statystyczne (informacje) pochodzą od poszczególnych jednostek danej zbiorowości.
Cecha statystyczna - to wlaściwości, które charakteryzują jednostkę zbiorowości statystycznej. Np. wzrost
Cechy zmienne - to takie właściwości jednostek statystycznych, którymi poszczególne jednostki danej zbiorowości różnią się od siebie. Każda jednostka statystyczna może być charakteryzowana przez różne cechy zmienne. (np. wiek, wzrost, płeć).
Cechy statystyczne stałe - to takie właściwości, które są wspólne wszystkim jednostkom danej zbiorowości statystycznej. Np. w zbiorowości studentów SGGW, cechą wspólna jest to iż każdy student ma indeks tej uczelni.
Podstawowe rodzaje cech statyststycznych zmiennych:
- cechy mierzalne (inaczej ilościowe) np. wiek, dochód, waga
- cechy niemierzalne (inaczej jakościowe) np. płeć, kolor oczu, wyznanie
Cechy niemierzalne to takie właściwości jednostek, które określa się słownie - nie mają miary, ponieważ reprezentują kategorię (np. płeć, kobieta; zawód: architekt)
Cechy mierzalne są to takie właściwości jednostek, które można zmierzyć i wyrazić liczbą wraz z określoną jednostką miary (np. wiek: 31lat, dochód: 3000zł)
Cechy ciągłe to te, które mogą przyjąć każdą dowolną wartość z określonego przedziału liczbowego (wszystkie pośrednie wartości z tego przedziału). Przy tym liczba miejsc po przecinku jest uzależniona od dokładności dokonywanych pomiarów (np. dwa miejsca po przecinku, jedno miejsce po przecinku, ale również zero miejsc po przecinku). Są one zatem wyrażone za pomocą liczb rzeczywistych. Mogą przyjmować nieskończenie wiele wartości.
Cechami ciągłymi są np.:
- wzrost
- wiek
- czas dojazdu do pracy
- powierzchnia mieszkania
Cechy mierzalne skokowe - to te, które mogą przyjmować tylko pewne, konkretne wartości liczbowe, nie przyjmując wartości pośrednich.
Cechami skokowymi są np.:
- liczba wizyt w kinie
- liczba osób w gospodarstwie domowym
- liczba wypadków drogowych w Warszawie w danym roku
Prezentacja danych
Szereg szczegółowy (wyliczający) jest najprostszą formą prezentacji danych. Stanowią go dane indywidualne (inaczej dane pierwotne) uporządkowane niemalejąco lub nierosnąco. Szereg taki uzyskujemy porządkując zebrane dane w kolejności od najmiejszej do największej lub od największej do najmniejszej.
Np. Badając wśród studentów liczbę wizyt w kinie w ciągu miesiąca:
Zebrane dane przedstawimy np. 0, 0, 1, 2, 3, 3, 5
Szereg strukturalny (rozdzielczy) otrzymujemy w wyniku podzielenia zbiorowości na grupy (klasy) ze względu na interesującą cechę statystyczną, przy czym określa się, ile jednostek należy do danej grupy. Tak więc szereg rozdzielczy jest tablicą, która składa się z dwóch kolumn (lub dwóch wierszy, jeśli zapisujemy go poziomo). W pierwszej kolumnie podane są wartości (warianty) cechy w podziale na grupy, natomiast w drugiej kolumnie podaje się ile jednostek ma dany wariant cechy (tj. ustala się liczebność klas).
Np. poziom wykształcenia w zbiorowości 60 pracowników spółki.
Szereg rozdzielczy punktowy tworzony jest dla cechy skokowej. Budowa tego szeregu jest analogiczna jak budowa szeregu rozdzielczego dla cechy jakościowej. Tak więc tablica zawierająca szereg rozdzielczy punktowy skłąda się z dwóch kolumn (lub dwóch wierszy jeśli zapisany jest w układzie poziomym), jedynie z tą różnicą, że w pierwszej kolumnie podajemy kolejno wartości cechy.
Np. Liczba wizyt w kinie 20 studentów.
Szereg rozdzielczy przedziałowy budujemy dla cech ciągłych. W pierwszej kolumnie tablicy umieszczamy przedziały, na jakie podzieliliśmy wartości cechy, w drugiej kolumnie - liczbę jednostek o wartościach cechy z danego przedziału liczbowego.
Np. Powierzchnia liczby 70 mieszkań w Osiedlu Słoneczna Osada.
Powierzchnia mieszkania |
Liczba mieszkań
|
20-50 |
8 |
50-80 |
12 |
RAZEM |
20 |
Szereg czasowy - prezentuje dane statystyczne w ujęciu dynamicznym. Jest on ciągiem wielkości badanego zjawiska (badanej cechy) obserwowanego w kolejnych jednostkach czasu. Tak więc szereg czasowy prezentuje zmiany zjawiska w czasie.
Badanym zjawiskiem może być np.:
- liczba zawartych małżeństw w kolejnych misiącach 2006r.
- liczba studentów SGGW w kolejnych latach w okresie 1997-2007
- liczba mieszkańców Polski na dzień 31 grudnia w latach 1990-2007.
Szereg przestrzenny - prezentuje dane statystyczne w ujęciu terytorialnym. Jest to ciąg wielkości badanego zjawiska (badanej cechy) obserwowanego w rozmieszczeniu przestrzennym. Tak więc szereg przestrzenny prezentuje terytorialne rozmieszczenie badanego zjawiska (cechy).
Np. Informacje o rocznym spożyciu piwa w litrach na jednego mieszkańca w 2005 r.
Kraj |
Spożycie piwa ( w l na 1 mieszkańca) |
Czechy |
155,0 |
USA |
82,0 |
Polska |
70,7 |
Etap 1: Ustalenie liczby klas.
Etap 2: Ustalenie rozpiętości przedziałów klasowych.
Etap 3: Ustalenie granic poszczególnych przedziałów.
Wzór: k![]()
![]()
gdzie:
k - zalecana liczba przedziałów klasowych n - liczebność zbiorowości
Wzór ten mówi, że liczba klas powinna być rowna w przybliżeniu pierwiastkowi kwadratowemu z liczebności zbiorowości.
Np. Liczebnośc zbiorowości wynosi 50
Przedziałów klasowych powinno więc być k![]()
7 przedziałów klasowych
Rozstęp oblicza się w bardzo prosty sposób. Mianowicie od najwyższej wartości cechy odejmuje się najniższą wartość. Oznaczając rozstęp literą R, możemy to działanie przedstawić nastepująco:
R=Xmax - Xmin gdzie: Xmax=najwyższa wartość cechy Xmin=najniższa -||-
Np. Wśród naszych danych najdłuższy czas wolny to 364minuty, a najkrótszy 26minut. Mamy więc: 364-26=338 Rozstęp równy jest 338 minut.
Teraz możemy obliczyć rozpiętość klas korzystając z równania:
ri=![]()
gdzie: i-numer klasy ; R- rozstęp; k - liczba klas
Z tego wzoru wynika że chcąc określić rozpiętość przedziału musimy rozstęp podzielić przez liczbę klas.
Np. Dla naszych danych o czasie wolnym mamy:
R=338 - to ustalony wcześniej rozstęp
K=7 - to ustalona wcześniej liczba klas więc:
R1=![]()
(minut)
Otrzymaliśmy więc, że rozpiętość przedziału powinna wynosić 48,3minut.
Aby ustalić granice poszczególnych przedziałów, musimy przede wszystkim podjąc decyzję jaka liczba będzie dolną granicą pierwszego przedziału (czyli lewym końcem tego przedziału). Otóż dolną granice pierwszego przedziału przyjmuje się zwykle wartość bliską (lub równą) wartości minimalnej w zbiorze danych, czyli Xmin. Wybór powinien być taki, aby zapewnić przejżystość szeregu oraz aby szereg obejmował najmniejszą wartość cechy.
Np. wracając do czasu wolnego Xmin=26min. Za dolną granicę pierwszego przedziału możemy przyjąć liczbę 25.
Ustalając końce kolejnych przedziałów należy pamiętać o zasadzie że dolne granice przedziałów następnych powinny być równe górnym granicom przedziałów poprzednich.
Np. Szereg rozdzielczy przedzialowy dla czasu wolnego. (przedziały prawostronnie domknięte)
Czas wolny w minutach |
Liczba osób |
25-75 |
5 |
75-125 |
5 |
RAZEM |
10 |
Szereg dwuwymiarowy ( dwucechowy) przedstawia rozkład dwoch cech w zbiorowości .
Liczebność klas - informuje, ile jest jednostek w danej zbiorowości.
Np. Biorąc pod uwage badany wcześniej czas:
Czas wolny w minutach |
Liczba osób |
25-75 |
5 |
75-125 |
5 |
RAZEM |
10 |
W klasie 1 (25-75min) liczebnośc klasy wynosi 5 osób
W klasie 2 (75-125min wolnych) liczebność klasy wynosi 5 osób.
Liczebnośc skumulowana danej klasy obliczamy dodając liczebnośc tej klasy i liczebności wszystkich klas ją poprzedzających. Na przykład liczebnośc skumulowaną trzeciej klasy obliczamy dodając liczebności klasy pierwszej, drugiej i trzeciej.
Np.
Powierzchnia mieszkania |
Liczba mieszkan |
Skumulowana liczba mieszkań |
Przedziały klasowe |
liczebnośc |
Liczebność skumulowana |
20-50 |
8 |
8 |
50-80 |
12 |
20 *bo 8+12=20 |
RAZEM |
20 |
x |
Liczebnośc skumulowana drugiej klasy równa 20 oznacza że 20 mieszkań ma powierzchnię od 20 do 80m2, lub mowiąc inaczej, że 20 mieszkań ma powierzchnię nieprzekraczającą 80m2 (przypominając że nasze przedziały są zamknięte prawostronnie, więc wartość 80 należy do przedziału drugiego).
Wskażnik struktury informuje jaką część całej zbiorowości stanowi dana klasa. Dokładniej mówiąć, jaką część liczebności całej zbiorowości stanowi liczebność danej klasy.
Wzór: Wi=![]()
gdzie: Ni - liczebnośc klasy o numerze i; n- liczebnosc calej zbiorowosci
Ważne: Poszczegolne skladniki struktury są liczbami mniejszymi od 1.
Np.
Powierzchnia mieszkania |
Liczba mieszkań
|
Wskażnik struktury |
Przedziały klasowe |
liczebnośc |
Częstosć względna |
20-50 |
8 |
0,4 |
50-80 |
12 |
0,6 |
RAZEM |
20 |
1,00 |
Interpretują liczby z powyższej tabeli możemy powiedzieć że:
- najmniejszych mieszkań o powierzchni 20-50m2) jest 8 co stanowi 40% ogółu zbadanych mieszkań
- największych mieszkań (o powierzchni 50-80m2) jest 12 co stanowi 60% ogółu zbadanych mieszkań
Skumulowany wskaźnik struktury (częstość skumulowana) danej klasy szeregu rozdzielczego określa, jaki jest udział liczebności skumulowanej tej klasy w liczebności całej zbiorowości.
Powierzchnia mieszkania |
Liczba mieszkan |
Skumulowana liczba mieszkań |
Skumulowany wskaznik struktury |
Przedziały klasowe |
liczebnośc |
Liczebność skumulowana |
Częstośc względna skumulowana |
20-50 |
8 |
8 |
0,40 |
50-80 |
12 |
20 *bo 8+12=20 |
1,00 |
RAZEM |
20 |
x |
x |
Wielkość 0,40 oznacza że:
- w badanej zbiorowości 8 mieszkań (40%) nie przekracza powierzchni 50m2
Gęstość liczebności jest to przeciętna liczba jednostek statystycznych, przypadająca na jednostkę długości przedziału. Obliczamy ją poprzez podzielenie liczebności i-tej klasy przez rozpiętość i-tej klasy. Np.
Wiek pracownika |
Liczba pracowników |
Rozpiętośc przedziału |
Gęstość liczebności |
16-25 |
18 |
9 |
2 (bo 18:9=2) |
25-30 |
15 |
5 |
3 (bo 15:5=3) |
RAZEM |
33 |
x |
x |
Wzór na wskaźnik podobieństwa struktur:
Gdzie: wp - wskaznik podobienstwa struktur
Wi, 1 - wskaznik struktury i-tej klasy w pierwszej zbiorowości
Wi,1- wskaznik struktury i-tej klasy w drugiej zbiorowości
Wskaźnik podobieństwa struktur jest liczbą z przedziału (0,1| . Oznacza to, że największa wartośc jaką może przyjąć jest 1. 0<wp<1
Przy czym:
Wskażnik podobieństwa struktur - służy do pomiaru siły podobieństwa struktur (dwu zbiorowości ze względu na tę samą cechę).
Możemy przyjąc następującą interpretację w zależności od tego, jaką wartość przyjmuje wskaźnik wp, :
Np. Podobieństwo struktur wyniosło 0,76. Wartośc 0,76 jest dość bliska jedności ( z przedziału 0,6 - 0,8). Świadczy ona o dużym podobieństwie porównywanych struktur. A zatem interpretując uzyskany wynik powiemy, że struktura mieszkań na powierzchni w obu spółdzielniach jest podobna.
39. Podaj przykład zastosowania (sporządź przykładowy rysunek) wykresu liniowego. Uwaga: pamiętaj o podpisaniu osi.
Wykresy liniowe stosowane są między innymi do prezentacji
- szeregów rozdzielczych przedziałowych
- szeregów czasowych, gdzie przedstawiają dynamikę zmian analizowanego zjawiska w czasie.
Chcąc sporządzić np wykres szeregu czasowego:
- na osi poziomej (x) odkłada się numery okresów
- na osi poziomej (y) poziom badanego zjawiska
40. Podaj przykład zastosowania (sporządź przykładowy rysunek) wykresu powierzchniowego. Uwaga: pamiętaj o podpisaniu osi.
Wykresy powierzchniowe służą między innymi do prezentacji:
- szeregów rozdzielczych z cechą niemierzalną
- szeregów rozdzielczych punktowych
- szeregów rozdzielczych przedziałowych.
41.Co rozumiemy pod pojęciem histogramu liczebności oraz histogramu częstości? Naszkicuj przykładowo jeden z nich. Uwaga: pamiętaj o podpisaniu osi.
a) Histogram liczebności jest to wykres ilustrujący liczebność np. liczebność mieszkań/powierzchnie mieszkań(m2)
b) Histogram częstości jest to wykres ilustrujący częstość czyli udział procentowy np. procent mieszkań/powierzchnia mieszkań(m2).
42.Co rozumiemy pod pojęciem histogramu liczebności skumulowanej oraz histogramu częstości skumulowanej? Naszkicuj przykładowo jeden z nich. Uwaga: pamiętaj o podpisaniu osi.
Histogram liczebności skumulowanej obrazuje liczebność skumulowaną zaś histogram częstosci skumulowanej obrazuje częstość skumulowaną. W histogramach skumulowanych charakterystyczny jest układ słupków. NIe może sie bowiem zdarzyć, że kolejny słupek będzie niższy od poprzedniego, niemniej może się zdarzyć, że sąsiadujące słupki będą miały takią samą wysokość.
43.Co rozumiemy pod pojęciem łamanej liczebności oraz łamanej częstości? Naszkicuj przykładowo jeden wykres. Uwaga: pamiętaj o podpisaniu osi.
Łamana liczebnosc lub częstość, czyli łamana prosta, jest to taka linia, która powstaje przez połączenie odcinkami środków górnych podstaw słupków histogramu prostego ( odpowiednio histogramu liczebności lub częstości). A zatem w celu sporządzenia takiej łąmanej zaznaczaymy w układzie współrzędnych punkty, które maja:
- odciętą ( na osi X) odpowiadającą środjkowi danego przedziału
- rzędną (os Y) odpowiadającą liczebności ( lub częstości) tego przedziału.
Następnie zaznaczone punkty łączymy odcinkami.
44.Co rozumiemy pod pojęciem łamanej liczebności skumulowanej oraz łamanej częstości skumulowanej? Naszkicuj przykładowo jeden wykres. Uwaga: pamiętaj o podpisaniu osi.
Łamaną liczebności (częstości) skumulowanej, czuli kumulantę, otrzymujemy przez połączenie odcinkami prawych końców górnych podstaw słupków histogramu skumulowanego (odpowiednio histogramu liczebności skumulowanej lub częstości skumulowanej). W celu sporządzenia takiej łąmanej zaznaczamy w układzie współrzędnych punkty, które mają:
- odciętą (oś X) odpowiadającą prawemu końcowi danego przedziału,
- rzędną (oś Y) odpowiadającą liczebności skumulowanej (lub częstości) tego przedziału.
Następnie zaznaczone punkty łączymy odcinkami.
45.Co rozumiemy pod pojęciem krzywej liczebności?
Krzywa liczebności jest jedną z form graficznej prezentacji rozkładu cechy statystycznej. Krzywą liczebności tworzymy w taki sam sposób, jak wielobok liczebności, z tym wyjątkiem, że zamiast łamaną, punkty na wykresie łączymy łagodnie przebiegającą krzywą.
46.Co rozumiemy pod pojęciem krzywej częstości?
Krzywa określająca związek możliwych wartości zjawiska z częstością jego występowania, jest jedną z form graficznej prezentacji rozkłądu cechy statystycznej. Krzywą tworzymy w taki sam sposób, jak wielobok liczebności, z tym wyjątkiem, że zamiast łamaną, punkty na wykresie łączymy łagodnie przebiegającą krzywą.
47. Jak rozumiemy pojęcie rozkładu symetrycznego?
W rozkładzie symetrycznym jednostki skupiają się przy środkowych wartościach cechy, rozłożone sa symetrycznie po obu stronach pewnej osi symetrii np. najwięcej mieszkań ma przeciętną powierzchnię. Można przy tym zaobserwować jedno lub więcej skupień jednostek.
- Rozkład jest jednomodalny kiedy jednostki skupiają się przy środkowej wartości cechy (odpowiada jej najwyższy, środkowy supek histogramu). W miarę oddalania się od wartości środkowej liczba jednostek maleje.
- Rozkład jest dwumodalny kiedy ma dwa skupienia jednostek. Jedno skupienie znajduje się przy najniższych wartościach cechy, a drugie przy najwyższych wartości cechy. W tym przypadku jednostek o środkowych wartościach cechy jest najmniej. Rozkłąd tego typu nazywa się rozkłądem siodłowym.
48.Sporządź przykładowy wykres rozkładu normalnego oraz dowolnego rozkładu symetrycznego, który nie jest rozkładem normalnym. Uwaga: pamiętaj o podpisaniu osi.
Rozkład normalny to rozkład teoretyczny, charakteryzujący się określonymi właściwościami. Jest on rozkładem symetrycznym (czyli liczebności odpowiadające wartościom zmiennej rozkładają się symetrycznie wokół liczebności największej). Każdy rozkład normalny jest rozkładem symetrycznym, ale nie każdy rozkład symetryczny jest rozkładem normalnym, ponieważ do rozkładów symetrycznych należą także rozkłady leptokurytyczne (czyli wysmukłe) oraz platokurtyczne (spłaszczone), które nie są normalnymi.
49.Jak rozumiemy pojęcie rozkładu o asymetrii prawostronnej?
Rozkład o asymetrii prawostronnej to taki rozkład, w którym jednostki mają tendencję do skupiania się przy niskich wartościach cechy np. najwięcej mieszkań ma niewielką powierzchnię.
50. Jak rozumiemy pojęcie rozkładu o asymetrii lewostronnej?
Rozkład o asymetrii lewostronnej to taki rozkład, w którym jednostki mają tendencję do skupiania się przy wysokich wartościach cechy np. najwięcej mieszkań ma dużą powierzchnię.
51.Jak rozumiemy pojęcie rozkładu jednomodalnego?
Rozkład jednomodalny to taki który ma jeden punkt skupienia jednostek.
52.Jak rozumiemy pojęcie rozkładu wielomodalnego?
Miary statystyczne (część 1)
Rozkład wielomodalny to taki który ma więcej niż jeden punkt skupienia jednostek.
Miary statystyczne (część 1)
53.Co rozumiemy pod pojęciem parametrów statystycznych? Podaj przykład dowolnego parametru wraz i interpretacją.
Parametry statystyczne sa to wielkosci liczbowe, które słuza do opisu struktury zbiorowosci statystycznej w sposób systematyczny. Brana jest pod uwage cała populacja.
Przykład
Kiedy Lincoln został wybrany po raz pierwszy na
prezydenta, dostał 39.82% sposród 1 865 908 oddanych
głosów. Jezeli przyjmiemy ilosc tych głosów za
populacje to 39.82% jest parametrem statystycznym a
nie statystyka.
54.Jak rozumiemy pojęcie statystyki z próby. Podaj dowolny przykład takiej statystyki wraz z interpretacją.
STATYSTYKA Z PRÓBY - zmienne losowe będące dowolną funkcją wyników próby losowej, np. średnia arytmetyczna wyników próby .
Przykład.
Spośród 200 studentów wydziału ekonomi losujemy 50 i obliczamy średnią ich wieku. Jest to przykład statystyki z próby.
55. Podaj klasyfikację miar statystycznych ze względu na kryterium związane z opisem własności rozkładu i podaj po jednym przykładzie miary z każdej grupy.
a) Położenie wartości cechy - miary przeciętne
b) Zróżnicowanie wartości cechy - miary dyspersji
c) Asymetrię rozkładu - miary skośności
d) Koncentrację - miary koncentracji
56. Wyjaśnij, jaką własność rozkładu pozwalają scharakteryzować miary położenia. Wymień trzy miary z tej grupy.
Miary położenia pozwalają określić gdzie w zbiorze wartości liczbowych znajdują się dane.
Przykładami miar położenia są: średnia arytmetyczna, średnia geometryczna,mediana.
57.Wyjaśnij, jaką własność rozkładu pozwalają scharakteryzować miary dyspersji. Wymień trzy miary z tej grupy.
Miary dyspersji pozwalają określić, jak bardzo zróżnicowane są jednostki statystyczne ze względu na wartość badanej cechy. Przykładami miar zróżnicowania są : odchylenie standardowe, wariancja, średnie odchylenie bezwzględne.
58.Wyjaśnij, jaką własność rozkładu pozwalają scharakteryzować miary asymetrii. Wymień trzy miary z tej grupy.
Miary asymetri pozwalają dostarczyć informacji na temat symetrii rozkładu lub jej braku.
Do przykładowych miar asymetrii rozkładu należą: współczynnik asymetrii, trzeci moment centralny, współczynnik skośności.
59. Wyjaśnij pojęcie koncentracji. Podaj przykład miary służącej do oceny stopnia koncentracji.
Miara koncentracji rozkładu to taka miara rozkładu, która wskazuje na nierównomierne rozdysponowanie wartości cechy pomiędzy elementy próby losowej. Przykładem jest Kurtoza.
60. Podaj klasyfikację miar ze względu na sposób ich wyznaczania i wyjaśnij użyte przez Ciebie pojęcia. Podaj po jednym przykładzie miary z każdej grupy.
61.Przedstaw (podaj nazwy i oznaczenie literowe) wraz z zastosowaniem znane Ci średnie klasyczne.
a) Średnia arytmetyczna - wyznacza się tylko dla cech wyrażonych w skali przedziałowej lib ilorazowej ( czyli dla cech mierzalnych). Obliczamy ją, sumując wartości cechy wszystkich jednostek zbiorowości, a następnie dzieląc otrzymaną sumę przez liczbę tych jednostek.
b) Średnia geometryczna - jest miara wykorzystywaną w zagadnieniach szczegolnych (np. analizie szeregów czasowych). Oblicza się ją jako pierwiastek stopnia n-tego z iloczynu n wartości. Wyznaczamy ją zatem, mnożąc poszczególne wartości cechy, a następnie z uzsykanego iloczynu wyciągamy pierwiastek takiego stopnia, ile było mnożonych osób.
c) średnia harmoniczna - stosuje się ją wówczas, kiedy wartości cechy podane są w jednostkach stosunkowych (tzw. łamanych) czyli jeśli cecha wyrażona jest w przeliczeniu na jednostkę innej cechy, na przykład:
- gęstość zaludnienia (liczba osób/km2)
- dochód na osobę(zł/os)
- prędkość ( km/godz)
62.Wymień (podaj nazwy i oznaczenie literowe) miary, które zaliczamy do średnich pozycyjnych (zarówno pierwszego rzędu, jak i wyższych rzędów).
a) dominanta - (wartość modalna lub moda) jest najczęściej stosowaną pozycyjną miarą położenia. Może być wyznaczana dla cech wyrażonych w dowolnej skali, a zatem również w skali nominalnej. Jest to jedyna miara położenia, która ma sens w przypadku analizy cech jakościowych. Dominanta jest to taka wartość cechy ( lub wariant w przypadku cech jakościowych), która w danej zbiorowości występuje najczęściej (dominuje). Oznacza to, że dominanta charakteryzuje jednostki o typowym poziomie cech.
b) mediana - można ją wyznaczyć dla cech wyrażonych w dowolnej skali z wyjątkiem nominalnej. Jest wartością cechy, jaką ma jednostka leżąca w środku uporządkowanego ciągu obserwacji. Tak więc mediana jest wartością cechy środkowej jednostk, czyli takiej, która leży w środku szeregu szczegółowego. Z tego względu mediana nazywana jest często wartością środkową. Numer jednostki środkowej( w szeregu szczeólowym) nazywa się pozycją mediany. Upraszczając zagadnienie można powiedzieć, że mediana dzieli zbiorowość statystyczną na dwie równe części w ten sposób, że połowa jednostek zbiorowości przyjmuje wartości mniejsze od mediany, natomiast druga połowa - wartości większe od mediany.
c)Kwantyle - definiuje się jako wartości cechy badanej zbiorowości, przedstawionej w postaci szeregu statystycznego, które dzielą zbiorowość na określone części pod względem liczby jednostek, części te pozostają do siebie w określonych proporcjach.
Kwartyl pierwszy Q1 - dzieli zbiorowość na dwie części w ten sposób, że 25% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu Q1, a 75% równe bądź wyższe od tego kwartyla
Kwartyl drugi (mediana Me) dzieli zbiorowość na dwie równe części; połowa jednostek ma wartości cechy mniejsze lub równe medianie, a połowa wartości cechy równe lub większe od Me; stąd nazwa wartość środkowa
Kwartyl trzeci Q3 dzieli zbiorowość na dwie części w ten sposób, że 75% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu Q3, a 25% równe bądź wyższe od tego kwartyla
Decyle np. decyl pierwszy oznacza, że 10% jednostek ma wartości cechy mniejsze bądź równe od decyla pierwszego, a 90% jednostek wartości cechy równe lub większe od decyla pirwszego
63. Przedstaw i wyjaśnij na przykładzie trzy wybrane własności średniej arytmetycznej.
(a) - wartość średniej arytmetycznej nie może być mniejsza od najniższej wartości wśród danych i jednocześnie nie może być większa od wartości najwyższej. Z zakresu danych 3,4,5,6 średnia nie może wynieść 3 i 6.
(b) - suma odchyleń obserwacji od ich średniej jest równa zero,
(c) - średnia arytmetyczna jest zawsze wyrażona w takich samych jednostkach miary jak badana cecha np (powierzchnia mieszkania), jak i średnia arytmetyczna wyrażone są w m2.
64.Przedstaw sposób wyznaczania średniej arytmetycznej z danych jednostkowych (podaj wzór wraz z wyjaśnieniem). Podaj liczbowy przykład tej miary i zinterpretuj, co oznacza podana przez Ciebie wartość.
x=x1+x2....+xn/n
wzór ! Przykład. Mamy 4 mieszkania o powierzchni: 44m2, 54m2, 60m2, 79m2, Oblicz średnią arytmetyczną. Rozwiązanie: 44+54+60+79/4 = 59,25. Wynik oznacz, że badane przez nas mieszkania mają średnio 59,25m2. Interpretując powiemy, że na jedno mieszkanie przypada 59.25m2 powierzchni(gdyby wszytskie mieszkania miały taką samą powierzchnię, to każde z nich miałoby 59,25m2)
65.Wyjaśnij sposób wyznaczania mediany z danych jednostkowych. Podaj liczbowy przykład tej miary i zinterpretuj, co oznacza podana przez Ciebie wartość.
Jeśli mamy natępujący zbiór danych:
1 2 4 6 7
wówczas bardzo łątwo wskazać medianę, gdyż łatwo znaleźć środek zbioru pięcioelementowego. Medianą jest wartość 4. Me=4
W przypadku zbioru danych parzystego dodajemy 2 srodkowe wartości i dzielimy je na 2. Medianą jest wynik.
66.Wyjaśnij sposób wyznaczania dominanty z danych jednostkowych. Podaj liczbowy przykład tej miary i zinterpretuj, co oznacza podana przez Ciebie wartość.
Wyznaczymy dominantę dla liczby wyjazdów służbowych w ciągu roku pracowników pewnego oddziału banku ( 15 osób) dane są następujące:
0 0 1 1 1 1 1 1 2 2 2 3 4 5 30.
Badanaą cechą jest tutaj liczba wyjazdów służbowych. Jest to cecha skokowa. Wyznaczenie dominanty polega w tym przypadku na wskazaniu, jaka liczba wyjazdów występuje najczęściej. Latwo zauważyć, że najczęściej występującą wartością cechy jest 1. A zatem dominanta jest równa 1 (wyjazd służbowy) czyli Do= 1 (wyjazd służbowy)
Interpretując obliczoną miarę powiemy, że w badanym oddziale banku największa liczba osób odbyła w ciągu roku 1 wyjazd służbowy, co oznacza, że typowy pracownik wyjechał 1 raz w ciągu roku.
67. Wyjaśnij sposób wyznaczania pierwszego kwartyla z danych jednostkowych. Podaj liczbowy przykład tej miary i zinterpretuj, co oznacza podana przez Ciebie wartość.
68. Wyjaśnij sposób wyznaczania trzeciego kwartyla z danych jednostkowych. Podaj liczbowy przykład tej miary i zinterpretuj, co oznacza podana przez Ciebie wartość.
Przy wyznaczaniu kwartyli postępujemy analogicznie jak przy wyznaczaniu mediany:
1) uporządkować dane ( w kolejności rosnącej lub malejącej)
2) wyznaczyć pozycję poszukiwanych kwartyli,
3) obliczyć (lub tylko wskazać) wartość interesujących kwartyli.
Przypadek przy parzystej liczbie obserwacji.
Poniższe dane dotyczą czasu dojazdu do pracy dwunastu pracowników spółki :
6 10 10 14 16 18 20 24 25 27 30 36 (minut)
Wyznaczanie kwartyli rozpoczniemy od mediany. Ponieważ liczba danych jest parzysta (n=12), więc mediana znajduje się pomiędzy dwiema środkowymi obserwacjami. W naszym przypadku pomiędzy liczbami 18 i 20. Wynosi więc:
18+20/2 = 19 min.
Po znalezieniu mediany, która podzieliła zbiorowość na połowy, wyznaczamy pozostałe kwartyle w analogiczny sposób, czyli znajdując środki powstałych dwoch częsci. Itrzymujemy:
q1= 10+14/2= 12 (minut) - kwartyl pierwszy
q3=25+27/2= 26 (minut) - kwartyl trzeci
Interpretując wartość kwartyla pierwszego równą 12 powiemy, że 25% osób dojeżdża w czasie krótszym niż 12 minut, a 75% dojeżdża w czasie dłuższym niż 12 minut. Natomiast kwartyl trzeci równy 26 oznacza, że 75% osób dojeżdża w czasie krótszym niż 26 minut, a 25% osób dojeżdża w czasie dłuższym niż 26 minut.
69.Wyjaśnij pojęcie decyli. Podaj liczbowy przykład dowolnego decyla i zinterpretuj, co oznacza podana przez Ciebie wartość.
Decyle to takie wartości cechy, które dzielą zbiorowość ( uporządkowany ciąg obserwacji) na 10 liczebnie równych części, czyli każda po 10% jednostek zbiorowości. Części te zwane są grupami decylowymi. Podział na 10 części daje 9 decyli.
Decyle wykorzystywane są np. w analizie wynagrodzeń.
- decyl pierwszy obliczony dla płac równy jest 2000zł oznacza, że 10% osób zarabia poniżej 2000zł, a 90% osób powyżej,
- decyl trzeci równy 2500zł oznacza, ze 30% osób zarabia poniżej tej kwoty, a 70% osób powyżej.
70.Wyjaśnij pojęcie centyli. Podaj liczbowy przykład dowolnego centyla i zinterpretuj, co oznacza podana przez Ciebie wartość.
Centyle(percentyle) to wartości cechy uzyskiwane przy podziale zbiorowości(uporzadkowanego ciągu obserwacji) na 100 liczebnie równych części, czyli każda po 1% jednostek zbiorowości. Części te zwane są grupami centylowymi. Podział na 100 części daje 99 centyli. Z podziałem centylowym mamy do czynienia przy analizie wielu kwestii społecznych. Na przykład badania poziomu inteligencji na podstawie poziomu ilorazu inteligencji IQ wskazują, że 98. centyl ilorazu inteligencji wynosi w Polsce 148. stanowią 2% całej populacji.
71. Wymień (podaj nazwy i oznaczenia literowe) znane Ci klasyczne miary dyspersji.
a) odchylenie przeciętne - d
b) wariancja - s^2
c) odchylenie standardowe - s
d) współczynnik zmienności ( klasyczny) - Vs
72. Wymień (podaj nazwy i oznaczenia literowe) znane Ci pozycyjne miary dyspersji.
a) rozstęp - R
b) rozstęp międzykwartylowy - Rq
c) odchylenie ćwiartkowe - Q
d) współczynnik zmienności (pozycyjny)- Vq
73.Wyjaśnij pojęcia miar bezwzględnych i miar względnych. Wyjaśnienie poprzyj przykładem.
Miary dzielą się na :
a) bezwzględne ( absolutne) które są wielkościami mianowanymi (tzn. mają miana, tj. jednoski miary takie, jak badana cecha)
b) względne ( inaczej relatywne), które są wielkościami niemianowanymi lub mogą być wyrażone w procentach.
Wśród wymienionych miar zróżnicwoania miarami względnymi są współczyniki zmienności (klasyczny i pozycyjny). Wszystkie pozostałe to miary bezwzględne.
74.Wyjaśnij pojęcie typowego obszaru zmienności. Wyjaśnienie poprzyj przykładem.
Za jednostki typowe w danej zbiorowości uznaje się te, których wartości cechy mieszczą się w przedziale (Me-Q; Me+Q).
Przykład:
Badano tygodniowe wydatki na owoce studentów pewnej uczelni. Otrzymano: medianę tych wydatków 15zł, kwartyl pierwszy 9 zł, kwartyl trzeci 17zł. Chcemy określić przedział, w jakim wahają się wydatki typowego studenta (typowy obszar zmienności)
Posiadamy następujące informacje:
Me=15, Q1=, Q3=17
Na ich podstawie możemy wyznaczyć pozycyjny typowy obszar zmienności. Odchylenie ćwiartkowe, zgodnie ze wzorem 3.13, wynosi:
Q=Q3-Q1/2=17-9/2=4 (zł)
A zatem pozycyjny typowy obszar zmienności dla tygodniowych wydatków na owoce (wzór 3.14) ma postać:
Me - Q < Xtyp < Me +Q,
czyli:
15-4 < Xtyp < 15+4
11 < Xtyp < 19
A zatem typowy student wydaje na owoce od 11 do 19 złotych tygodniowo.
75.Przedstaw wzór na odchylenie standardowe. Podaj przykład liczbowy tej miary i zinterpretuj, co oznacza podana przez Ciebie wartość.
S=pierwiastek z s2 s2= wariancja
Przykład:
Wiek braci Iksińskich. Obliczamy odchylenie standardowe wieku tych braci.
16 10 14 5 5 lat
Aby wyznaczyć odchylenie standardowe, należy w pierwszej kolejności obliczyć wariancję. Obliczymy ją dwoma sposobami. Wykorzystamy wzór definiujący wariancję.
Obliczenia:
W celu obliczenia wariancji skorzystamy ze wzoru s2= (X1-X)2+(x2-x)2+....(xn-x)2/n
Średnia arytmetyczna wieku braci x=10 lat
Obliczenia prowadzimy tabelarycznie:
kwadrat odchyleń
x1-x =16 - 10= 6 36
x2- x=10 - 10=0 0 n=5
x3 -x=14 - 10=4 16 s2=102/5=20,4
-5 25
-5 25
SUMA = 0 102
Tak więc suma naszych różnic pondniesionych do kwadratu wynosi:
(X1-X)2+(x2-x)2+....(xn-x)2/n = 102
Ponieważ n=5, więc wariancja wynosi s2=102/5=20,4(lat2)
76. Wyjaśnij pojęcie współczynnika zmienności. Podaj liczbowy przykład dowolnego współczynnika zmienności i zinterpretuj, co oznacza podana przez Ciebie wartość.
Współczynnik zmienności jest względną miarą zróżnicowania. Nie jest on uzależniony od przyjętej jednostki miary (jest wielkością mianowaną, ewentualnie wyrażoną w procentach)
Wykorzystuje się go gdy chcemy:
- ocenić siłę zróżnicowania analizowanej cechy
- porównać rozproszenie różnych cech w tej samej zbiorowości
- porównać rozproszenie tej samej cechy w różnych zbiorowościach.
Przykład:
Posiadamy następujące informacje dotyczące rocznych dochodów w dwóch grupach społecznych:
Grupa społeczna A Grupa społeczna B
x= 60 tys x=18 tys
s= 5 tys s= 3 tys
Która grupa społeczna charakteryzuje się większm zróżnicowaniem dochodów?
Odpowiedzi na postawione pytanie nie możemy udzielić na podstawie bezpośrednich porównań odchyleń standardowych. Jak wiadomo, odchylenie standardowe informuje o tym, jakie jest srednie odchylenie od sredniej srytmetycznej. Tak wiec nie wolno porownywac odchylen standardowych w przypadku, gdy srednie wrytmetyczne badanych zbiorowosci sa rozne. U nas wystepuje wlasnie taka sytuacja. Srednie dochody w obu grupach sa inne, przy czym w grupie A sa one duzo wyzsze niz w grupie B. Tak wiec stwierdzenie, ze odchylenie standardowe 5 tys wskazuje na wieksze zroznicowanie niz odchylenie 3 tys jest bledne. A zatem w celu porównania zróznicowania dochodów w danych grupach należy odnieść te odchylenia do średniej, czyli obliczyć wspolczynniki zmiennosci. Oto obliczenia:
grupa spoleczna A Grupa spoleczna B
Vs= S/X x 100% = 5/6 x 100% Vs= S/X x 100%= 3/18x100%
Vs=8,3% Vs= 16,7%
W grupie A wspolczynnik zmiennosci Vs jest rowny 8,3% co oznacza że odchylenie standardowe dochodów stanowi tu tylko 8,3% sredniej dochodów. Jak wiadmo taka wartosc wspolczynnika zmiennosci swiadczy o slabym zroznicowaniu dochodow. W grupie B wspolczynnik zmiennosci wynosi 16,7% czyli odchylenie standardowe dochodow stanowi w tej grupie 16,7 % sredniej, co okreslimy jako zroznicowanie umiarkowane. Tak wiec grupa B charakteryzuje sie wiekszym zroznicowaniem dochodow.
77.Podaj wzór na dowolny współczynnik asymetrii i wyjaśnij, jak interpretuje się jego wartość.
Wskaźnik skośności - Wsk=X = Do
gdzie:
x- srednia arytmetyczna
Do - dominanta
Wskaźnik skośności wyznacza kierunek asymetrii:
Wsk = 0 - rozkład symetryczny
Wsk > 0 - asymetria prawostronna
Wsk < 0 - asymetria lewostronna
![]()
Wyszukiwarka
Podobne podstrony:
Stat FiR TEORIA I (podstawowe pojecia, sggw - finanse i rachunkowość, studia, II semestr, Statystyka
Stat FiR TEORIA I (podstawowe pojecia, sggw - finanse i rachunkowość, studia, II semestr, Statystyka
Stat FiR TEORIA II (miary cd, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Stat FiR TEORIA III (estymacja, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
QUIZ egzaminacyjny Statystyka opisowa(2), sggw - finanse i rachunkowość, studia, II semestr, Statyst
QUIZ egzaminacyjny Statystyka matematyczna(2), sggw - finanse i rachunkowość, studia, II semestr, St
Budżet Państwa, sggw - finanse i rachunkowość, studia, II semestr, Finanse Ćw
DOCHODY BUD»ETU PAĐSTWA W 2010 R, sggw - finanse i rachunkowość, studia, II semestr, Finanse Ćw
D.Grabowski fir grupa 1b projekt(pralki), sggw - finanse i rachunkowość, studia, III semsstr, ekonom
Finanse publiczne - pytania z egzaminu, Uniwersytet Ekonomiczny w Katowicach, Finanse i Rachunkowość
Zadanie 1, sggw - finanse i rachunkowość, studia, III semsstr, ekonomika, ekonomika
Grupa A-1, sggw - finanse i rachunkowość, studia, IV semstr, ekonometria, EKONOMETRIA OD Kaczorek
Ankieta badanie w banku 2013TK, sggw - finanse i rachunkowość, studia, 6 semestr, marketing
Wykład II Ekonomika i Organizacja Przedsiębiorstw, sggw - finanse i rachunkowość, studia, III semss
Rachunek wynikow, sggw - finanse i rachunkowość, studia, III semsstr, ekonomika, ekonomika
Rachunek zysków i stratll, sggw - finanse i rachunkowość, studia, III semsstr, ekonomika, ekonomika
więcej podobnych podstron