E(r_p) = x_R
R + (1 - x_R)
E (r_m.) średnia oczekiwana stopa zwrotu

x_R - część funduszy inwestora

R - stopa wolna od ryzyka

E (r_m.) - oczekiwana stopa zwrotu z portfela rynkowego

σ_p = (1 - x_R)
σ_m. = x_m.
σ_m. ryzyko optymalnego portfela

σ_p. - odchylenie standardowe stóp zwrotu z nowego portfela p

σ_m. - odchylenie standardowe stóp zwrotu z portfela rynkowego

x_R + x_m. = 1 oraz x_m. = 1 - x_R

Zad. 1.

Przyjmijmy, że odchylenie standardowe stóp zwrotu z portfela rynkowego σ_m. = 20%, oczekiwana stopa zwrotu E(r_m.) = 14%, a stopa wolna od ryzyka stanowi R = 9% tego portfela. Jakiego dochodu może się spodziewać przedsiębiorca inwestując 50 % swoich środków w instrumenty wolne od ryzyka a pozostałe 50% w portfel rynkowy? Jakie jest ryzyko portfela 50 - 50?

E(r_p) = x_R
R + (1 - x_R)
E (r_m.) = 50%
9% + (1 - 0,5)
14% = 11,5 %

σ_p = (1 - x_R)
σ_m. = x_m.
σ_m. = (1 - 0,5)
20% = 10%

Zad. 2.

Przypuśćmy, że jesteś zainteresowany zainwestowaniem 60% twoich środków w portfel rynkowy i 40% w instrumenty pozbawione ryzyka. Jaka jest oczekiwana stopa zwrotu i ryzyko z portfela 60 - 40? Przyjmij, że oczekiwana stopa zwrotu z portfela rynkowego wynosi 15% a odchylenie standardowe 25%. Stopa wolna od ryzyka R = 10%

E(r_p) = x_R
R + (1 - x_R)
E (r_m.) = 40%
10% + (1 - 0,4)
15% = 13 %

σ_p = (1 - x_R)
σ_m. = x_m.
σ_m. = (1 - 0,4)
25% = 15%

Zad. 3.

Dla sytuacji z zadania 2 odpowiedz na następujące pytanie. Jeżeli pożyczyłeś środki pieniężne i x_R = - 0,5 i zainwestowałeś 150% twoich środków w portfel rynkowy, czyli że x_m. = 1,5 to jaka będzie oczekiwana stopa zwrotu z twojej inwestycji?

E(r_p) = x_R
R + (1 - x_R)
E (r_m.) = (-0,5)
10% + (1 + 0,5)
15% = 17,5 %

σ_p = (1 - x_R)
σ_m. = x_m.
σ_m. = (1 + 0,5)
25% = 37,5%

Zad. 6

Roczne stopy zwrotu z akcji spółki i rynku podano poniżej:

Rok stopy zwrotu rynkowe stopy zwrotu (WIG)

19X1 -5% -6%

19X2 14% 16%

19X3 10% 12%

19X4 12% 14%

19X5 17% 20%

1. oblicz współczynnik beta dla firmy

2. jaki procent ryzyka całkowitego firmy stanowi ryzyko systematyczne

ad. a)

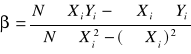
współczynnik beta

X_i - stopa rynkowa zwrotu

Y_i - stopa zwrotu z danej akcji

N - liczba obserwacji

Rok Y_i X_i X_i² X_iY_i Y_i²

19X1 -5% -6% 36 30 25

19X2 14% 16% 256 224 196

19X3 10% 12% 144 120 100

19X4 12% 14% 196 168 144

19X5 17% 20% 400 340 289

suma 48 56 1032 882 754

=

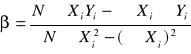
ad. b)

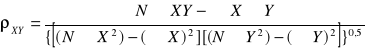
współczynnik korelacji

(0,99968)² = 0,99936 lub 99,94 % jest systematyczne

---