136. DLACZEGO WARINACJA KRIGINGOWA NIE MOŻE BYĆ TRAKTOWANA JAKO MIARA JAKOŚCI ESTYMACJI? JAK NALEŻY JĄ INTERPRETOWAĆ?

Wariancja krigingowa czyli ten błąd estymacji nie może być traktowana jako realna miara jakości estymacji (była w początkach rozwoju geostatystyki traktowana jako realna miara błędu)

Ponieważ to nie jest prawdziwy błąd, tylko pewna względna miara pokazująca zróżnicowanie błędów wynikające z konfiguracji przestrzennej danych pomiarowych, z geometrycznego układu punktu danych w stosunku do lokalizacji która ma być estymowana.

• czyli nie pokazuje rzeczywistego błędu estymacji

• 
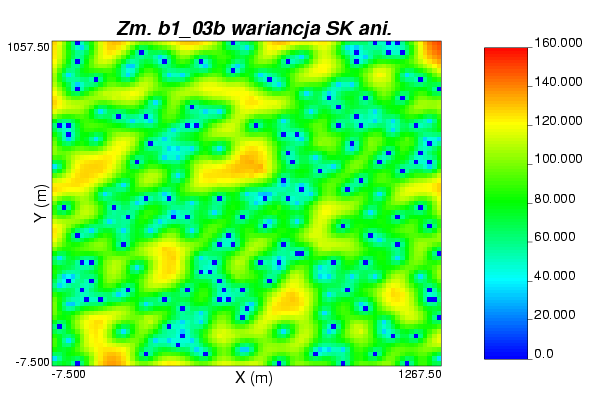
  to jest względny błąd estymacji

Interpretacja:

• jest zerowa w punktach pomiarowych i rośnie w miarę oddalanie się od miejsc pomiarów

• czyli ona jest największa tam gdzie są największe odległości między punktami danych i największa jest tam gdzie na krawędziach punkty pomiarowe nie otaczają ze wszystkich stron tego obszaru

137.DLACZEGO MIMO, ŻE ESTYMATORY KRIGINGOWE SĄ NIEOBCIĄŻONE, ROZKŁAD DANYCH ESTYMOWANYCH RÓŻNI SIĘ OD RZECZYWISTYCH?

Estymatory krigingowe są nieobciążone, czyli one powodują ze na całym obszarze błędy ujemne i dodatnie się niwelują i średni błąd jest 0. Chodzi o to, by metoda nie dawała regularnie wartości za niskich i za wysokich. (minimalizacja wariancji błędu).

- w miejscach gdzie wykonano pomiar wartość jest taka sama jak zmierzono i algorytm estymacyjny powoduje że odchylenia wartości rzeczywistych od wyestymowanych globalnie się zerują

- tzn. że tyle samo błędów ujemnych co dodatnich

- czyli tak jest zbudowany ten algorytm że wiemy, że w przybliżeniu średni błąd jest 0

to minimalizacja wariancji błędu

Ale mimo to ten rozkład danych estymowanych różni się od rzeczywistych, ponieważ estymacja mimo że honoruje dane to nie honoruje ich struktury przestrzennej jak to ma miejsce w przypadku symulacji. Estymacja powoduje wygładzenie rzeczywistości (stanowi tylko jej przybliżenie)

zmniejszona jest wariancja danych, ale też zmniejszone jest zróżnicowanie danych modelowanych w stosunku do rzeczywistych

- tzn. że minima i maksima na mapie estymowanej są ścięte w stosunku do rzeczywistych pomiarów ( niedoszacowuje maksima i przeszacowuje minima )

Tendencja do tworzenia powierzchni trendu z dala od danych

- to bardzo niekorzystna cecha danych estymowanych (gdzie są gęsto punkty pomiarowe - obraz estymowany jest bardzo zróżnicowany, dopasowując się do punktów pomiarowych, ale jak odległość między punktami jest bardzo duża - to mapa robi się bardzo łagodna)

- daje fałszywych obraz

- widać na powierzchni estymowanej gdzie były wykonywane pomiary

Wśród dostępnych algorytmów automatycznej estymacji mamy dwie grupy (nie są to grupy rozłączne): „wierne” i „wygładzające”. Estymatory wierne pozostawiają oryginalne dane pomiarowe nienaruszone, tzn. jeśli punkt estymowany przypada w miejscu punktu pomiarowego podawana jest wartość oryginalna. W algorytmach wygładzających tworzony jest pewien model struktury przestrzennej analizowanego zjawiska, a wartość estymowana jest średnią ważoną wyników pomiarów z co najmniej kilku blisko leżących punktów. Nawet jeśli lokalizacja punktu pomiarowego i szacowanego jest identyczna - wynik pomiaru i estymacji różnią się. Estymator najczęściej „obcina” ekstrema i w tym sensie ma charakter „wygładzający”.

Uznajemy zazwyczaj, że im bardziej estymator wiernie oddaje oryginalne dane pomiarowe, tym jest lepszy. Okazuje się, że nie zawsze taka ocena jest uzasadniona, skoro np. to właśnie przy użyciu algorytmów wygładzających można zredukować błędy estymacji wynikające zarówno z niedokładnych pomiarów, jak i z nieprecyzyjnej informacji o lokalizacji punktów pomiarowych. Estymator krigingowy jest nieobciążony globalnie (odchylenia wyników na plus i na minus się równoważą, średnia błędu jest zbliżona do zera), ale nie lokalnie (rozkład statystyczny wyników estymacji różni się od rzeczywistego, na małych powierzchniach błędy się nie równoważą).

138.CZEMU MIMO CIĄGŁEGO DOSKONALENIA ALGORYTMÓW NUMERYCZNYCH W DALSZYM CIĄGU PREFEROWANE JEST MANUALNE MODELOWANIE SEMIWARIOGRAMU, TAK JAK SIĘ TO ROBI W VARIOWINIE?

Manualne modelowanie semiwariogramu jest preferowane ponieważ w analizach geostatystycznych bardzo liczy się wiedza na temat analizowanych danych i badanego zjawiska. Badający może wprowadzić do modelu anizotropię, mimo że nie widać jej wyraźnie np. na powierzchni semiwariogramu, ponieważ zna charakter badanego zjawiska. Automatyczne metody modelowania semiwariogramu dążą wyłącznie do osiągania jak najlepszych wartości wskaźników dopasowania (ważonej sumy kwadratów, AIC itp.). Mogą nie oddawać prawdziwej struktury zjawiska. Przy skomplikowanej strukturze przestrzennej zjawiska (anizotropia na różnych kierunkach i odległościach, wiele struktur) modelowanie może się okazać zadaniem zbyt trudnym dla komputera - nie ma dobrych algorytmów używanych do tego celu. W przyrodzie często mamy do czynienia z bardzo złożonymi strukturami, których wymodelowanie automatyczne jest niemożliwe

139.W JAKIEJ PROCEDURZE STOSUJE SIĘ WAŻONĄ SUMĘ KWADRATÓW (WSS)? JAKIE STOSUJE SIĘ W NIEJ WAGI? WYMIEŃ WADY I ZALETY KAŻDEJ Z NICH.

Ważoną sumę kwadratów stosuje się w półautomatycznym modelowaniu semiwariogramu do porównania „dobroci”/dokładności dopasowania (goodness-of-fit) struktur wybranych przez użytkownika do wartości semiwariogramu empirycznego.

Wagi mogą być nadawane proporcjonalnie do ilości par (1), z których została wyliczona semiwariancja w danym odstępie. W ten sposób jednak pierwsze odstępy mają mniejszą wagę.

Żeby temu zapobiec stosuje się także ilość par podzieloną przez podniesioną do kwadratu wartość modelu odpowiadającą danemu odstępowi (2), która jest niższa w pierwszych odstępach.

W programie Vesper można użyć także odchylenia standardowego średniej semiwariancji dla danego odstępu (1/std_dev) oraz ilorazu ilości par i odchylenia standardowego (No_pairs/std_dev).

1 - N(h_k)

2 - N(h_k)/[γ(h_k)]²

140. KTÓRY Z POWSZECHNIE STOSOWANYCH MODELI SEMIWARIOGRAMU MOŻE POWODOWAĆ „NIESTABILNOŚĆ” UKŁADU RÓWNAŃ KRIGINGU I DAWAĆ NIEREALISTYCZNE ESTYMACJE? JAK MOŻNA TEGO UNIKNĄĆ?

Niestbilność układu równań krigingu może być spowodowana użyciem modelu gaussowskiego do analizy i modelowania struktury przestrzennej zjawiska.

-ponieważ stanowi granicę zmienności losowej

-i to jest jakby granica zjawisk losowych, za tym jest już tylko zmienność o charakterze deterministycznym, którą można opisywać normalnymi funkcjami regresyjnymi

• model ten ze względu na swój deterministyczny charakter* daje w wielu przypadkach nierealistyczne wyniki estymacji tzw. artefakty, nie mające związku ze strukturą przestrzenną zjawiska.

• więc nie może być stosowany samodzielnie tzn. nie może być obliczane/ estymowane jakieś zjawisko na podstawie modelu który jest tylko gaussowski musi być zawsze dodany nugget lub też model gaussowski jest elementem modelu złożonego

• jego użycie jest czasami uzasadnione przy analizie przestrzennej i prognozowaniu parametru o bardzo regularnej i łagodnej zmienności przestrzennej np. rzeźba na obszarach młodoglacjalnych, poziom wód gruntowych w obszarach o mało zróżnicowanej rzeźbie i jednolitej budowie geologicznej

Aby tego uniknąć poleca się dodać niewielką wariancję nuggetową. Wg P. Goovaertsa najlepszym rozwiązaniem jest nie stosować modelu Gaussowskiego w ogóle.

Jeśli semiwariogram empiryczny ukazuje kształt podobny do modelu Gaussowskiego, możemy do modelowania pierwszej struktury użyć modelu potęgowego. Uzyskujemy w ten sposób odzwierciedlenie łagodnie zmieniającej się struktury na pierwszych odstępach.

Jeśli semiwariogram empiryczny ukazuje zarówno asymptotę (prostą) i krzywą powinno się używać modelowania następującą funkcją

gdzie parametr ω można regulować.

141. CZEMU BARDZO RZADKO STOSUJE SIĘ AUTOMATYCZNE MODELOWANIE SEMIWARIOGRAMU?

W przyrodzie często mamy do czynienia z bardzo złożonymi strukturami, których wymodelowanie automatyczne jest niemożliwe. A dobrze dopasowany model stanowi podstawę do dalszej prawidłowej estymacji. Dlatego stosuje się modelowanie ręczne, przy wykorzystaniu wiedzy eksperta geostatystyka.

W analizach geostatystycznych bardzo liczy się wiedza na temat analizowanych danych i badanego zjawiska. Automatyczne metody modelowania semiwariogramu dążą wyłącznie do osiągania jak najlepszych wartości wskaźników dopasowania (ważonej sumy kwadratów, AIC itp.). Mogą nie oddawać prawdziwej struktury zjawiska. Badający może wprowadzić do modelu anizotropię, mimo że nie widać jej wyraźnie np. na powierzchni semiwariogramu, ponieważ zna charakter badanego zjawiska.

142.PODAJ PRZYKŁADY ZASTOSOWAŃ KOKRIGINGU, KIEDY ZMIENNA UZUPEŁNIAJĄCA DOTYCZY POMIARÓW TEJ SAMEJ CECHY CO ZMIENNA PIERWOTNA.

Przykładem może być wykorzystanie tańszych i szybszych, ale mniej dokładnych pomiarów pH gleby wykonanych za pomocą papierka lakmusowego do estymacji pobranych rzadziej, ale dokładniejszych próbek pH gleby analizowanych w laboratorium. Praktycznym wykorzystaniem takiego działania może być badanie gleby na potrzeby precyzyjnego rolnictwa.

• np. zawartość substancji organicznej (pobór próbek i zdjęcie lotnicze)

• przykład: sytuacja z opadami i cyfrowym modelem rzeźby terenu:

• cyfrowy model terenu mamy o takiej rozdzielczości że w zasadzie moglibyśmy estymacje opadów robić w takiej samej siatce 130 m (to nie ma oczywiście sensu)

• czyli mamy wysokość terenu każdego posterunku pomiarowego (1 warunek)

• zmienna wtórna jest znana na całym obszarze, w każdej lokalizacji gdzie byśmy chcieli wykonać estymacje

144.CO TO JEST EFEKT WYGŁADZANIA (SMOOTHING EFFECT) , I OD CZEGO ON ZALEŻY?

Efekt wygładzania w krigingu polega na tym, że wartości wyestymowane mają mniejszą wariancję niż dane, co najczęściej nie zgadza się z rzeczywistym rozkładem analizowanej zmiennej. Wygładzanie jest większe w miejscach oddalonych od punktów z danymi, mniejsze blisko tych punktów. Z tego powodu na mapy uzyskane metodą krigingu mogą ukazywać większe zróżnicowanie zjawiska na pewnych obszarach tylko dlatego, że były one gęściej opróbowane. Ponadto na takich mapach wartości ekstremalne będą występować tylko w miejscach próbek, w miejscach gdzie wartości są uzyskane z estymacji wartości niskie będą zawyżone, a wartości wysokie zaniżone.

145.CO TO JEST „HOMOSCEDASCITY”?

Jest to tzw. homogeniczność wariancji, która oznacza, że wariancja jednej zmiennej jest taka sama dla wszystkich odpowiadających jej wartości drugiej zmiennej.

Lokalna wariancja danych jest różna w różnych miejscach badanego obszaru (nonstationarity), czyli warunek homogeniczności wariancji nie jest spełniony

wariancja krigingowa nie może być traktowana jako miara jakości estymacji względna miara

estymator jest efektywny ma niewielką wariancję

---