Analiza kowariancji
Analiza kowariancji
Aby przeprowadzić analizę kowariancji czyli współzmienności dla dwóch różnych cech, niezbędne jest posiadanie następujących obliczeń:
odwróconej, zredukowanej macierzy obserwacji,
zredukowanych wektorów danych,
wektorów stałych,
danych wyjściowych.
Wyniki obliczeń zamieszczone będą w tabelach skonstruowanych wg poniższego schematu (każda para cech ma osobną tabelę) np.:
Kowariancja cechy I i II
Źródło zmienności |
df (liczba stopni swobody) |
SMM (suma iloczynów mieszanych) |
MSMM (średni kwadrat) |
k |
Komponent kowariancji |
Efekt samca |
Liczba samców - 1 |
Wyjaśnienie w punkcie 2 kon-spektu |
SMM samca / df samca |
Wartość taka sama jak przy analizie wariancji |
(MSMM samca - MSMM błędu) / k dla samca |
Efekt stada |
Liczba stad - 1 |
Wyjaśnienie w punkcie 2 kon-spektu |
|
|
|
Efekt roku |
Liczba lat - 1 |
Wyjaśnienie w punkcie 2 kon-spektu |
|
|
|
Efekt sezonu |
Liczba sezonów - 1 |
Wyjaśnienie w punkcie 2 kon-spektu |
|
|
|
Błąd |
Liczba obserwacji - df samców - df stad - df lat - df sezonów - 1 |
Wyjaśnienie w punkcie 3 kon-spektu |
SMM błędu / df błędu |
|
|
Obliczanie sumy iloczynów mieszanych dla efektu samca.
Analiza kowariancji może być prowadzona dla wszystkich efektów głównych. Jednakże ze względu na to iż niezbędny do dalszych obliczeń będzie komponent kowariancji dla efektu samca, ograniczymy obliczenia do tego jednego efektu.
Aby obliczyć sumę iloczynów mieszanych np. dla samca należy:
Wykorzystać macierze obserwacji i wektory stałych dla poszczególnych efektów głównych. Poniższy schemat przedstawia które elementy macierzy obserwacji i wektorów stałych odpowiadają poszczególnym efektom (dokładnie te same co w analizie wariancji).
Aby obliczyć sumę iloczynów mieszanych dla cechy I i II dla efektu samca, należy:
pomnożyć transponowany wycinek wektora stałych dla cechy I przez odwrócony wycinek odwróconej macierzy obserwacji, a otrzymany wynik pomnożyć przez wycinek wektora stałych przed transponowaniem dla cechy II (odpowiadający efektowi samca). Efektem będzie jedna liczba, która jest sumą iloczynów mieszanych dla efektu samca dla cechy I i II.
Aby obliczyć dla efektu samca sumy iloczynów mieszanych dla par cech II i III oraz I i III, należy posłużyć się tym samym fragmentem macierzy obserwacji ale wykorzystać odpowiednie wycinki wektorów stałych dla właściwych cech. Schemat obliczeń jest taki sam.
Wyniki wpisywać do wynikowych tabeli analizy kowariancji dla cechy I i II, I i III oraz II i III.
Obliczenie sumy iloczynów mieszanych dla błędu
Aby obliczyć sumę iloczynów mieszanych dla błędu trzeba dokonać obliczenia dwóch wartości:
Ogólna suma iloczynów mieszanych dla danej pary cech:
Ogólną sumę iloczynów mieszanych np. dla pary cechy I i II obliczamy mnożąc odpowiadające sobie wartości cechy I i cechy II (w programie MsExcel wykonać to można wykorzystując formuły podane na poniższym rysunku).
Po przemnożeniu pierwszej wartości, przeciągamy (kopiujemy) formułę na pozostałe komórki, a następnie otrzymane wartości sumujemy z wykorzystaniem formuły „SUMA”.
Podobnie postępujemy z pozostałymi parami cech, czyli I i II oraz II i III.
Poprawka R
Aby otrzymać wartość R dla pary cech I i II mnożymy wektor stałych dla cechy I przez zredukowany wektor obserwacji dla cechy II. Aby było to możliwe należy najpierw wykonać transponowanie wektora stałych.
Transponowany wektor stałych mnożymy przez wektor obserwacji wg znanego schematu mnożenia dwóch macierzy (instrukcja w konspekcie o macierzach). Wynikiem mnożenia dwóch wektorów jest jedna liczba.
Otrzymaną poprawkę R odejmujemy od ogólnej sumy iloczynów mieszanych i w ten sposób otrzymujemy
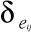
- sumę iloczynów mieszanych dla błędu dla pary cech I i II.Podobnie postępujemy z pozostałymi parami cech.
Wyszukiwarka
Podobne podstrony:
ANALIZA PRZYPADKU, metody
METODY PRACY HODOWLANEJegz inz, Zootechnika, Metody hodowlane
metody hodowlane
Analiza treści metody badań 1
13 WYZNACZENIE ŚRODKA ZGINANIA b, Budownictwo PG, sem4, MDwAK, Metody doświadczalne w analizie konst
Macierze, Metody hodowlane
metody hodowlane 2.m, Metody hodowlane
Metody hodowli i identyfikacji grzybów drożdżopodobnych i dimorficznych
Krytyczna analiza epistemologicznej metody ateizmu
Met Hod - kolokwium 1, Metody hodowlane
Zagadnienia z gentyki, Metody hodowlane
Met Hod - kolokwium 2, Metody hodowlane
metody hodowlan e pytania kolos3, Zootechnika, Metody hodowlane
trusek hołownia, procesy membranowe, METODY HODOWLI DROBNOUSTROJÓW
Cz 10 Instrumentalne metody analizy ilościowej Metody chromatograficzne
odziedziczalnosc korelacje, Metody hodowlane
więcej podobnych podstron